模块化多电平换流器无环流仿真模型

石吉银，唐志军，林国栋，李超，晁武杰，邹焕雄

(国网福建省电力有限公司电力科学研究院，福州市350007)

模块化多电平换流器无环流仿真模型

石吉银，唐志军，林国栋，李超，晁武杰，邹焕雄

(国网福建省电力有限公司电力科学研究院，福州市350007)

为简化仿真控制策略和提高仿真效率，对桥臂环流抑制功能投入的模块化多电平换流器(MMC)进行整体建模，提出一种无环流仿真模型。首先分析了MMC单个子模块工作的电气特性，然后以此为基础推导出换流器相单元电容电压之和与交、直流侧电气量的关系，最后对三相相单元进行整体建模得到反映换流器外特性的仿真模型。在MATLAB中利用模型搭建柔性直流输电系统并对各种运行工况进行仿真，其仿真结果与基于RTDS详细模型仿真结果一致，充分说明了本文模型的可行性与准确性。该模型适用于仅关注换流器外特性的场合，具有仿真速度快、仿真精度高、适用性广的特点。

柔性直流输电;模块化多电平换流器(MMC);无环流仿真模型;子模块;等效建模

0 引言

柔性直流输电系统可以快速地对有功和无功两个目标进行独立调节，具有可控性好、运行方式灵活、适用场合多等优点。采用模块化多电平换流器(modular multilevelconverter，MMC)的柔性直流输电系统，随着电压等级和输送容量的提升，桥臂串联的子模块数目越来越多。在近期投运的厦门柔性直流输电工程中，单个桥臂的子模块数达216个，双站双极的子模块总数超过5 000个。对于大规模子模块群组成的换流器，若采用器件详细模型进行建模仿真，则其仿真速度将极其缓慢［1-2］。

近年来，如何对子模块进行简化等效，建立加速仿真模型成为学术界研究的热点。在所提出的加速仿真模型中，按其简化的对象主要可以分为3类。第1类模型以子模块为等效简化的对象。文献［3］利用半桥子模块投入或者切除状态上、下桥臂互补通断的特性，将4个电力电子器件等效为2个开关，从而简化支路数目;文献［4］将单个子模块从桥臂独立出来，串接电流值为桥臂电流的受控电流源形成单独回路，桥臂电压等效成值为各子模块电压之和的受控电压源，并将计算过程中的大规模矩阵分解为相应数目的小矩阵，以达到提速的效果;文献［2，5－7］对单个子模块建立戴维南等效模型后对N个子模块进行代数叠加，将各个桥臂等效为电阻和电压源串联的支路，该方法在保证仿真精度的情况下大大提高了仿真速度。第1类模型能仿真各个子模块充、放电过程，最大限度保留了各个子模块的电气量信息，但随着子模块数目的增加，其仿真速度至少以线性速度降低［1］。第2类模型以换流器桥臂为等效简化的对象。文献［8］对各子模块建立开关函数，利用各子模块电容电压相等的假设推导出桥臂的等效开关函数以及等效桥臂电容;文献［9］利用平均化的子模块电气量信息推导出桥臂电气量的特征，将桥臂电容等效为一集中电容，而将桥臂输出电压等效为受控于集中电容电压的电压源;文献［10］提出将MMC桥臂等效为自定义数值计算模块与受控电压源组合的数值计算详细模型，并通过简化MMC的电压均衡控制及子模块状态的差异性，建立了数值计算平均值模型。第2类模型不考虑子模块电容电压均压过程，仿真速度快，但需要加入桥臂环流控制策略，以抑制MMC换流器内二倍频环流。第3类模型以换流器为等效简化的对象，文献［11］利用功率平衡的原理，推导出换流器交、直流侧的电气关系，建立交、直流侧仅存在电气二次信息联系的解耦模型;由于计及功率平衡的子模块未区分投入和切除状态，其动态响应不准确。另外，文献［11］的模型不能仿真换流器闭锁运行状态，且存在暂态故障过程中仿真精度不足的问题［12］。文献［12］在文献［11］的基础上提出改进方案，在拓扑结构中增加若干二极管和开关元件，以改善模型在闭锁、双极短路和单极短路状态下的性能，但是同样存在动态响应不准确的问题。

在控制系统设计、主设备参数选择、交直流网络系统级仿真等场合，用户并不关心换流器内部各子模块的工作状态，而是希望找到可以反映换流器外特性的高效仿真模型。本文以环流抑制功能投入后的模块化多电平换流器为研究对象，分析了换流器相单元电容电压和与交、直流侧电气量的关系，以此为基础提出一种反映换流器外特性的无环流仿真模型。

1 MMC拓扑结构及子模块运行特性分析

MMC拓扑结构如图1所示。MMC正常运行时，各相单元投入的子模块总数保持不变，以维持直流侧电压Udc恒定。通过改变各相上、下桥臂投入的子模块数目来输出正弦阶梯波［13］。子模块的电容值、初始电压、充电时间和充电电流等因素会影响到电容电压，使得各桥臂电容电压和存在差异，会在三相相单元之间产生二倍频环流［14］。

子模块处于不同运行状态时，其端口输出不同的电压［9］。子模块处于投入状态，即T1导通、T2关断时，端电压usm为电容电压uc。子模块处于切除状态，即T1关断、T2导通时，端电压usm为0。当T1和T2均关断时，子模块处于闭锁状态，交流系统对子模块进行不控充电或者保护动作闭锁换流阀后子模块均为该状态。子模块闭锁状态下，当电流ism为正方向时，电容C被充电;当电流ism为反方向时，电容C处于旁路状态。

图1 MMC拓扑结构图Fig.1 MMCtopology

2 MMC无环流模型建模

解锁状态下，相单元中各子模块处于投入或切除状态(不考虑旁路状态子模块)。对图1所示A相相单元进行分析，对于A相上桥臂第i个子模块，若为投入状态的子模块，其电气量状态方程为

对于A相上桥臂切除状态的子模块，其电气量状态方程为

假设A相上桥臂投入子模块数为npa，下桥臂投入子模块数为nna，上桥臂和下桥臂投入子模块总数为N。用(1)、(2)式对上桥臂所有子模块求和，可得

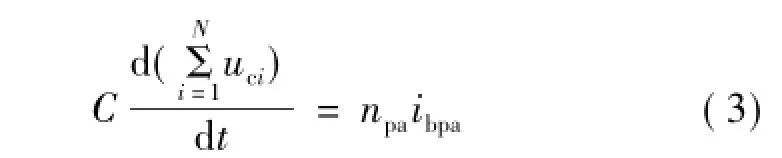
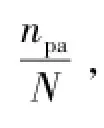
假设各子模块已均压，则A相上桥臂子模块输出电压总和ubpa可表示为

对式(4)、(6)进行相加可得:

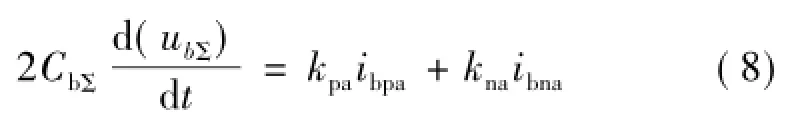
又桥臂电流［13］可表示为

将式(9)代入式(8)并结合kpa和kna的定义可得:

设控制系统计算的 A相参考电压为urefa，并设子模块额定工作电压为Ue，则kpa和kna［13］可表示为

而换流器的A相上桥臂参考电压和A相交流侧电流可表示为

其中φ为功率因数角，则由式(10)、(11)和(12)得:

同理，对于B、C相相单元可分别列出式(15)、(16):

式(14)、(15)和(16)中2倍频电流分量仅在三相桥臂之间流动，直流侧和交流侧均不存在此分量。因此，可将3个相单元看成整体，对式(14)、(15)和(16)进行求和，可得:

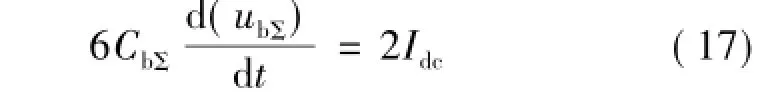
式(17)表明，将换流器视为由三相相单元投入电容并联的整体后其输出电流恒定，该式表征了换流器直流侧等效的外特性。据此，可将换流器所有子模块的电容等效为一集中电容，其值为6 CbΣ。结合式(4)—(7)，考虑B、C相相类似的表达式，可得解锁状态下换流器的等效模型，其等效电路如图2所示。

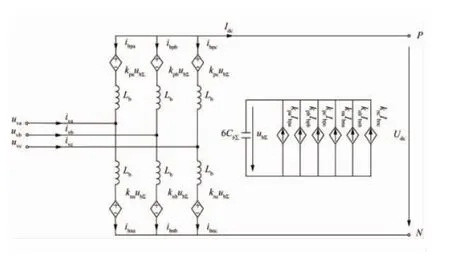
图2 解锁状态MMC无环流仿真模型等效电路图Fig.2 EquivalentcircuitdiagramofMMCsimulation modelwithoutcirculatingcurrentinde-blockstate

该等效模型中，通过调节各相相单元上桥臂kpj(j=A、B、C)、下桥臂knj(j=A、B、C)的值输出交流电压，各相单元kpj和knj之和保持为1，因此各相单元输出电压之和相等，不会产生环流，是对MMC换流器环流抑制功能投入状态的等效模拟。

为使模型能够仿真换流阀闭锁状态，对图2电路进行简单修改，增加充电二极管D1、D2和解锁开关K，并将各桥臂对等效电容充电的电流由桥臂电流ib修改为受控电压源的电流ic，得到图3所示的MMC无环流仿真模型等效电路。图3中，K闭合时模拟解锁状态，其电路与图2的电路一致;K断开时模拟闭锁状态，此时，需要令 kpj、knj(j=A、B、C)均为1。

此外，在换流器不控整流充电阶段，MMC换流器3个上桥臂和3个下桥臂各有1个桥臂处于充电状态，因此充电回路等效电容为2 CbΣ。设充电回路等效电阻为Req，则其充电时间常数为

但每个桥臂仅导通1/3周期，因此，换流器的充电时间常数为

易知，在不控整流状态下，由于kpj、knj(j=A、B、C)均为1，图3所示的电路充电时间常数也为τc，说明图3等效电路也适用于该状态。

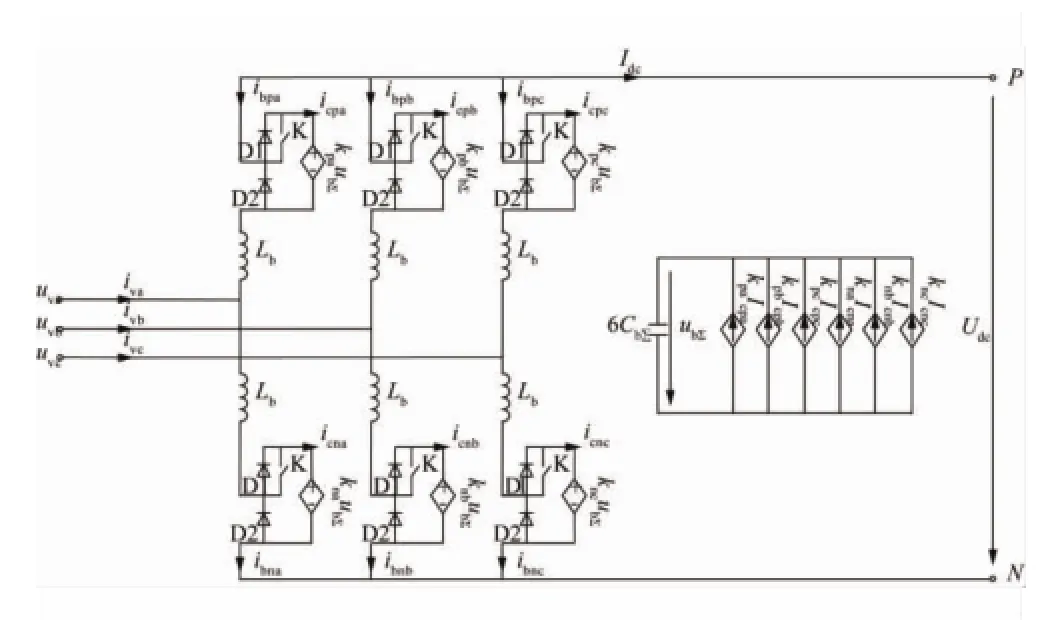
图3 MMC无环流仿真模型等效电路图Fig.3 EquivalentcircuitdiagramofMMC simulationmodelwithoutcirculatingcurrent

3 实例仿真分析

为验证本文 MMC仿真模型的正确性，在MATLAB和RTDS上分别搭建图4所示的柔性直流输电仿真系统，MATLAB采用图3仿真模型，RTDS仿真采用FPGA_GM详细模型，两种仿真采用相同的控制策略及控制参数。其中，站1采用有功功率+无功功率控制方式，站2采用直流电压+交流电压控制方式。两站采用的控制策略包含［15-18］:外环电压/功率控制策略、内环电流解耦控制策略、桥臂环流控制策略(仅RTDS仿真)、NLC控制策略等。

仿真系统参数如表1所示。

图4 仿真系统图Fig.4 Diagramofsimulationsystem

表1 仿真系统参数表Table1 Simulationsystemparameters

3.1充电过程

在站1模拟MMC启动充电过程，在旁路断路器QF1处于断开状态下，0.2 s仿真时刻合上交流侧断路器CB1，通过充电电阻对换流器充电。充电过程直流侧电压及交流侧电流波形见图5。

图5 MMC充电过程波形图Fig.5 WaveformofMMCchargingprocess

3.2解锁过程

两站均充电结束后，在相对仿真时间0.2 s对控直流电压站发出解锁换流阀命令，闭合解锁开关K，解锁过程见图6。

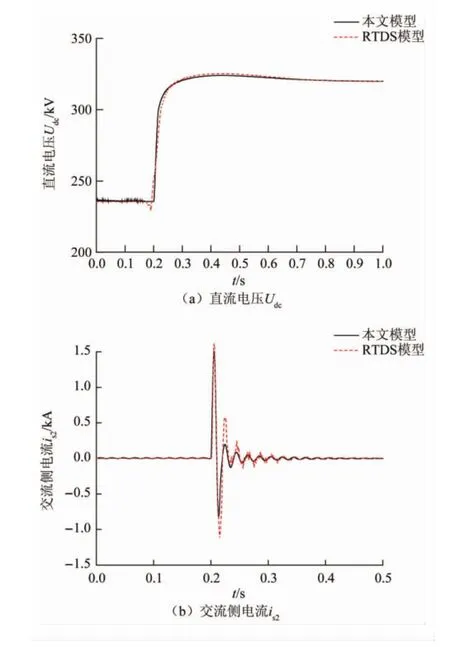
图6MMC解锁过程波形图Fig.6 WaveformofMMCde-blockprocess

3.3稳态运行

设置站1有功功率为200 MW，无功功率为100 MV·A;设置站2直流电压指令为320 kV，交流电压指令为230 kV。在仿真时间1.0 s时，RTDS仿真投入环流抑制功能，站1稳态运行波形见图7。图7(a)为RTDS环流抑制功能投入前桥臂电流与本文模型仿真波形的对比图，其中RTDS波形存在明显畸变，与本文模型仿真波形差异较大;图7(b)为RTDS环流抑制功能投入之后与本文模型仿真波形的对比图，二者完全重合。

3.4动态响应

分别进行直流电压、交流电压、有功功率、无功功率阶跃响应试验，阶跃量分别为10 kV，－2 kV，200 MW，200 MV·A，动态响应波形见图8。

图7 MMC稳态运行波形图Fig.7 WaveformofMMCsteady-staterunning

3.5暂态故障响应

站1有功功率设置为200 MW，无功功率设置为－100 MV·A。在2.0 s仿真时刻，模拟M1母线发生A相单相接地瞬时故障，接地电阻为1.0Ω，持续时间为100 ms。暂态故障响应波形见图9，其中图9 (b)交流侧电流已滤除零序分量。

由仿真波形可知，充电过程、解锁过程、稳态运行、动态响应及暂态故障响应实例仿真中，本文模型仿真波形与RTDS模型仿真波形一致，充分说明了本文模型的正确性。

图8 MMC阶跃响应波形图Fig.8 WaveformofMMCstepresponse

图9 MMC暂态故障响应波形图Fig.9 WaveformofMMCtransientfaultresponse

需要特别说明的是，在动态响应方面，文献［11－12］已提出的第3类仿真模型只有在子模块电容足够大时才适用。文献［12］仿真结果表明，子模块电容为10 mF时其模型依然不适用。本文模型仿真案例中，子模块电容为10 mF，动态响应精度依然很高，说明其适用性更佳。

4 结论

本文提出了一种MMC无环流仿真模型并详细介绍了其建模方法。该模型属于第3类仿真模型，相对于已经提出的第3类仿真模型，其电气量关系更准确，建模过程更简单。实例仿真结果表明，该模型仿真精度与RTDS详细模型非常接近，充分说明了本文模型的正确性。使用该模型进行柔性直流输电系统仿真时，控制策略无须考虑子模块电容均压和桥臂环流抑制问题，具有仿真速度快、适用性好等优点。该模型可以仿真任意电平数的换流器，非常适合仅考虑换流器外特性的仿真场合。

［1］许建中，李承昱，熊岩，等．模块化多电平换流器高效建模方法综述［J］．中国电机工程学报，2015，35(13):3381!3392．XU Jianzhong，LI Chengyu，XIONG Yan，et al．A review of efficient modeling methods for modular multilevel converters［J］．Proceedings of the CSEE，2015，35(13):3381-3392．

［2］GNANARATHNA U N，GOLE A M，JAYASINGHE R P．Efficient modeling of modular multilevel HVDC converters(MMC)on electromagnetic transient simulation programs［J］． IEEE Transactions on Pow er Delivery，2011，26(1):316-324．

［3］管敏渊，徐政．模块化多电平换流器的快速电磁暂态仿真方法［J］．电力自动化设备，2012，32(6):36-40．GUAN Minyuan，XU Zheng．Fast electro-magnetic transient simulation method for modular multilevel converter［J］．Electric Power Automation Equipment，2012，32(6):36-40．

［4］许建中，赵成勇，刘文静．超大规模MMC电磁暂态仿真提速模型［J］．中国电机工程学报，2013，33(10):114-120．XU Jianzhong，ZHAO Chengyong，LIU Wenjing．Accelerated model of ultra-large scale MMC in electromagnetic transient simulations［J］．Proceedings of the CSEE，2013，33(10): 114-120．

［5］许建中，赵成勇，ANIRUDDHA M G．模块化多电平换流器戴维南等效整体建模方法［J］．中国电机工程学报，2015，35(8): 1919-1928．XU Jianzhong，ZHAO Chengyong，ANIRUDDHA M G．Research on the Thevenin's Equivalent based Integral Modeling Method of the modular multilevel converter(MMC)［J］．Proceedings of the CSEE，2015，35(8):1919-1928．

［6］许建中．模块化多电平换流器电磁暂态高效建模方法研究［D］．北京:华北电力大学，2014．XU Jianzhong．Research on the electromagnetic transient efficient modeling method of modular multilevel converter［D］．Beijing: North China Electric Power University，2014．

［7］郭琦，王嘉钰，林雪华，等．提高MMC高效电磁暂态模型仿真精度的方法［J］．电力建设，2016，37(6):49-54．GUO Qi，WANG Jiayu，LIN Xuehua，et al．Improvement of highefficiency electromagnetic transient model simulation precision of MMC［J］．Electric Power Construction，2016，37(6):49-54．

［8］SAAD H，DENNETIERE S，MAHSEREDJIAN J，et al．Modular multilevel converter models for electomagnetic transients［J］．IEEE Transaction on Pow er Delivery，2014，29(3):1481-1489．

［9］郭高朋，胡学浩，温家良，等．基于大规模子模块群的MMC建模与快速仿真算法［J］．电网技术，2015，39(5):1226-1232．GUO Gaopeng，HU Xuehao，WEN Jialiang，et al．A large-scale submodule group based algorithm for modeling and high-speed simulation of modular multilevel converter［J］．Pow er System Technology，2015，39(5):1226-1232．

［10］喻锋，王西田，林卫星，等．模块化多电平换流器快速电磁暂态仿真模型［J］．电网技术，2015，39(1):257-263．YU Feng， WANG Xitian， LIN Weixing， et al． Fast electromagnetic transient simulation models of modular multilevel converter［J］．Pow er System Technology，2015，39(1) : 257-263．

［11］PERALTA J，SAAD H，DENNETIERE S，et al．Detailed and averaged models for a 401-level MMC-HVDC system［J］．IEEE Transactions on Pow er Delivery，2012，27(3):1501-1508．

［12］XU J Z，GOLE A M，ZHAO C Y．The use of averaged-value model of modular multilevel converter in DC grid［J］．IEEE Transaction on Pow er Delivery，2015，30(2):519-528．

［13］潘伟勇．模块化多电平输电系统控制和保护策略研究［D］．杭州:浙江大学，2012．PAN Weiyong．Research on control and protection strategy of modular multilevel converter-HVDC systems［D］．Hangzhou: Zhejiang University，2012．

［14］张建坡，赵成勇．模块化多电平换流器环流及抑制策略研究［J］．电工技术学报，2013，28(10):328-336．ZHANG Jianpo，ZHAO Chengyong．Research on circulation current and suppressing strategy of modular multilevel converter［J］．Transactions of China Electrotechnical Society，2013，28 (10):328-336．

［15］陈海荣，张静，屠卿瑞．电网电压不平衡时电压源换流器型直流输电的负序电压补偿控制［J］．高电压技术，2011，37(10): 2363-2369．CHEN Hairong，ZHANG Jing，TU Qingrui．Negative voltage compensating control of voltage source converter based HVDC system under unbalanced grid conditions［J］．High Voltage Engineering，2011，37(10):2363-2369．

［16］管敏渊，徐政，潘武略，等．电网故障时模块化多电平换流器高压输电直流系统的分析与控制［J］．高电压技术，2013，39(5): 1238-1245．GUAN Minyuan，XU Zheng，PAN Wulue，et al．Analysis and control of modular multilevel converter based HVDC transmission systems during grid faults［J］．High Voltage Engineering，2013，39 (5):1238-1245．

［17］王朝明，王华广，王睛．基于双PI控制器的模块化多电平变换器环流抑制策略［J］．电网技术，2014，38(10):2905-2912．WANG Chaoming，WANG Huaguang，WANG Qing．A dual PI controller based strategy to suppress circulating current in modular multilevel converter［J］．Power System Technology，2014，38 (10):2905-2912．

［18］赵倩，张群，严兵，等．柔性直流输电系统控制策略及动模试验［J］．电力建设，2015，36(12):57-62．ZHAO Qian，ZHANG Qun，YAN Bing，et al．Control strategy and dynamic simulation test of VSC-HVDC system［J］．Electric Pow er Construction，2015，36(12):57-62．

(编辑 刘文莹)

A Simulation Model Without Circulating Current of Modular Multilevel Converter

SHI Jiyin，TANG Zhijun，LIN Guodong，LI Chao，CHAO Wujie，ZOU Huanxiong

(Electric Power Research Institute of State Grid Fujian Electric Power Company Limited，Fuzhou 350007，China)

In order to simplify the simulation control strategies and improve the simulation efficiency，this paper proposes a simulation model without circulating current by integral modeling of modular multilevel converter(MMC) running under the bridge arm circulating current suppression function．Firstly the electrical characteristics of the single submodule of the MMC were analyzed，on the basis of which the relationship between the total capacitor voltage of the phase unit and the electric parameters of the AC and DC side was then derived，finally the three-phase unit was integral modeled to achieve the external characteristic of the converter．We used this model to build a flexible HVDC system in MATLAB and carry out the simulation in various operating conditions，whose simulation results agreed with the detailed model simulation results based on RTDS．It fully demonstrates the feasibility and accuracy of the proposed model．This model is suitable for the situation where only the external characteristics of the converter are concerned，and it has the characteristics of high speed，high accuracy and wide applicability．

flexible HVDC;modular multilevel converter(MMC);simulation model without circulating current;submodule;equivalent modeling

TM 72

A

1000－7229(2017)03－0027－07

10.3969/j．issn.1000－7229.2017.03.004

2016-10-14

石吉银(1981)，男，硕士，高级工程师，主要研究方向为电力系统继电保护、柔性直流输电技术;

唐志军(1972)，男，硕士，高级工程师，主要研究方向为电力系统继电保护、柔性直流输电技术;

林国栋(1974)，男，高级工程师，主要研究方向为电力系统继电保护、柔性直流输电技术;

李超(1983)，男，博士，高级工程师，主要研究方向为柔性直流输电技术;

晁武杰(1982)，男，博士，工程师，主要研究方向为柔性直流输电技术;

邹焕雄(1985)，男，工程师，主要研究方向为电力系统继电保护、柔性直流输电技术。