考虑脆性损伤和渗流的圆形水工隧洞稳定性分析

刘怀付

(1. 安徽理工大学 深部煤矿采动响应与灾害防控重点实验室，安徽 淮南 232001；2. 安徽理工大学 能源与安全学院，安徽 淮南 232001)

0　引言

地下水工隧洞是水利水电工程中重要引水建筑物，由于荷载、渗流场和内水压力的作用，将对隧洞围岩和支护结构产生渗流体积力和动水压力，改变隧道开挖后二次和三次应力状态，严重影响着隧洞范围和周围应力的分布。因此，在水工隧洞结构设计中，正确地进行塑性范围确定、应力分析和支护对工程的安全与经济具有重要意义。

传统隧洞弹塑性解[1]是在不考虑渗流和损伤对隧洞影响情况下得到的；采用Hoek-Brown[2](H-B)准则或Mohr-Coulomb[3-4](M-C)强度准则对巷道进行弹塑性分析，忽略中间主应力σ2的影响，会使结果偏于保守；脆性岩石达到应力峰值后具有应力值陡降、变形较小的特点，文献[5-7]中很少有对岩石脆性特性的考虑；围岩进入损伤阶段后，常将其简化为线性模型来处理[8-9]，而在脆性岩石物理模型试验中，超过峰值应变后，应力应变曲线会表现出明显的非线性[10]；在对隧洞进行衬砌时，常用支护阻力简单地代替衬砌应力，没有考虑衬砌与围岩的应力协调[11]；文献[12]结合具体工程问题，分析了不同衬砌系数、注浆半径等对渗流量和衬砌外水压力等影响规律，但未涉及围岩应力变形等力学问题分析。很多学者对隧洞弹塑性解析解进行了广泛研究，但对隧洞的研究多集中在某一或某几方面，所得结果与实际情况存有差异。

基于前人的研究，本文考虑隧洞围岩与衬砌的相互作用和非线性脆性损伤，利用统一强度理论推导出隧洞塑性范围和周边应力分布表达式，结合具体算例，分析了相关参数对塑性范围及衬砌和围岩应力分布的影响；用渗流量变化表征围岩渗透性变化，提出采用注浆加固圈进行支护，通过降低围岩渗透性来减小塑性范围和隧洞衬砌应力。所得结果可为隧洞稳定性分析和支护提供一定的理论指导和建议。

1　理论分析模型

1.1　隧洞力学模型

假设隧洞断面为圆形，围岩均质、各向同性，隧洞深埋且长度足够大。图1为深部水工隧洞模型，隧洞的内半径为R0，隧洞内半径R0处的孔隙水压力为pm；衬砌半径为R1，隧洞塑性区半径为R2；在隧洞半径R3以外处的渗流场与初始渗流场水压pi相同；内水压力ps均匀地作用在隧洞洞壁处；初始地应力p0和孔隙水压力pi作用在无穷远处。

图1　隧洞断面Fig.1　Calculation sketch of tunnel

1.2　统一强度准则

岩土工程中假定压应力为正、拉应力为负，隧洞围岩为弹脆塑性材料且满足平面应变条件，采用统一强度理论来描述隧洞围岩的强度特征，表达式为[13]

(1)

(2)

1.3　脆性岩体损伤本构关系

周维垣等[10]基于连续介质损伤力学理论，从岩体的损伤机理出发，提出了岩体的脆性损伤本构模型，在单轴压缩条件下，其应力-应变关系如图2所示。

图2　损伤模型应力-应变关系Fig.2　Stress-strain relationship of the damage model

将峰值强度前的应力应变关系简化为线弹性关系，峰值强度后的损伤为非线性各向同性损伤，用损伤变量可描述塑性区各个阶段的损伤演化过程。忽略峰值强度前的初始损伤，单轴压缩下的一维损伤演化方程为：

(3)

式中：D为损伤变量，D=0时表示岩石无损伤状态，D=1时表示岩石完全损伤，岩石破坏；ε为单轴压缩下的应变；εs和εc分别为峰值应力对应的应变和常量；n表征岩石脆性强弱的参数，n的值越大，岩石脆性越强。

将一维损伤本构方程推广到三维损伤，根据有效应力与Lemaitre应变等价原理，则三向应力情况下有：

(4)

式中：εi为等效应变。

平面应变条件下几何方程为：

(5)

式中：εr与εθ分别代表塑性区的切向应变和塑性应变；u为巷道位移；r为巷道中心轴线到围岩某一处的距离。

将式(5)代入(4)，并考虑弹塑性交界处变形连续条件:εi|r = R2=εc，可得塑性区围岩的等效应变为：

(6)

将式(6)代入式(3)中，可得三维应力状态下的损伤演化方程为：

(7)

式中：D(r)为损伤变量，其值与隧洞半径r有关；R2为隧洞塑性区半径；n表征岩石脆性强弱的参数。

1.4　渗流场计算

忽略围岩因塑性变形造成的渗透系数变化，施工期围岩渗透水压力可以认为是运行期在pm=0时的一种特殊情况，本文仅考虑运行期。根据文献[14]知运行期围岩的衬砌、孔隙水压力为：

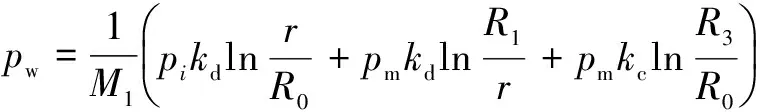
(8)

(9)

其中：

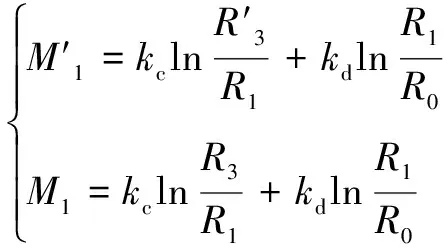
(10)

式中：kc、kd分别为衬砌混凝土和隧洞围岩的渗透系数；R3为施工期保持原始渗流场外水压力pi的围岩半径，可由钻孔实测或抽水试验确定。

2　隧洞应力分析

2.1　塑性损伤区应力

(11)

考虑孔隙水压力，围岩任一研究单元满足平衡微分方程：

(12)

式中：η为渗透水压力作用面积系数。

设p1为衬砌与围岩塑性区交界处径向应力；联立式(11)和式(12)并积分，以σr|r = R1=p1为边界条件，可得塑性区应力为：

(13)

其中：

(14)

2.2　弹性区应力

设弹塑性交界处径向应力为py，隧洞弹性区视为受py、地应力p0和孔隙水压力pw共同作用下的厚壁圆筒，可知弹性区应力：

(15)

在弹塑性交界面处，弹性区应力满足式(11)，且此时D=0，整理可得：

(16)

考虑弹塑性交界处径向应力连续，即σrp|r = R2=σre|r = R2。联立式(13)，(15)和(16)可得：

(17)

2.3　衬砌应力

假设衬砌为理想弹性材料，不发生塑性变形。衬砌与围岩共同承载，不考虑混凝土的损伤，假定衬砌满足统一强度准则，即：

(18)

其中：

(19)

将式(8)，(18)代入式(12)，进行积分并结合边界条件：σrp|r = R0=ps；可得衬砌应力为：

(20)

其中：

(21)

衬砌与围岩相互作用，塑性区与衬砌交界处径向应力连续：即σr|r = R1=p1；代入式(20)可得：

(22)

联立求解式(17)，(22)，可求得塑性区半径R2的隐式表达式为：

(23)

式(19)是关于塑性半径R2的超越方程，可通过迭代法求得；将R2代入式(22)得p1；再由式(13)，(15)和(17)可求得隧洞塑性区、弹性区和衬砌应力。

3　算例分析

在抽水试验过程中，在某一半径内会发生水头降，超过这一半径就不会发生水头降，这一半径叫做抽水影响半径，即在影响半径R3以外处的渗流场与初始渗流场水压pi相同。根据文献[16]可知，影响半径R3仅与岩体渗透系数kd、稳定流抽水降深Sw、出水量Q、抽水段长度l和钻孔半径rw有关，采用文献[16]中的相关参数，根据影响半径计算公式可得R3=24 m。

考虑切向应力σθ为最大主应力，对围岩起控制作用，故分析各个参数对塑性区半径R2和切向应力σθ的影响。

表1　n和(εc/εs)的关系

3.1　围岩与衬砌渗透比kd/kc对隧洞的影响

如图3，4分别为塑性区半径R2和切向应力σθ随渗透比kd/kc的变化示意图。由图3可知：当脆性参数n一定时，随kd/kc的增大，塑性区半径逐渐增大；当n分别为4，5，6，7和8时，kd/kc=5 000对应的R2比η=0所对应的R2分别增大了4.1%，4.6%，4.8%，4.4%，5.1%。由图3可知：σθ在隧洞塑性区与衬砌交界处和弹塑性交界处不连续，前者不连续是因为围岩和混凝土二者材料参数不同，后者不连续是因为塑性区围岩发生脆性损伤导致围岩力学性能发生劣化；衬砌内边界初始σθ不受kd/kc的影响；当kd/kc增大时，衬砌切向应力σθ逐渐增大，塑性区切向应力σθ逐渐减小且应力峰值逐渐远离塑性区内边界。因此，当围岩与衬砌渗透比差别较大时，不能把二者渗透比等同来处理，要全面考虑渗透比和渗流对隧洞的影响。

图3　b=0.5时渗透比kd/kc与R2的关系Fig.3　Relation between permeability ratio of kd/kcand R2 when b=0.5

图4　b=0.5和n=4时渗透比kd/kc与σθ的关系Fig.4　Relation between permeability ratio of kd/kcand σθ when b=0.5 and n=4

3.2　中间主应力系数b对隧洞的影响

如图5和6分别为塑性区半径R2和切向应力σθ随中间主应力系数b的变化示意图。由图5可知：脆性参数n一定时，随b的增大，塑性区半径逐渐减小，当n分别为4，5，6，7和8时，b=1对应的R2比b=0所对应的R2分别减少了3.5%，3.1%，3.3%，3.7%，4%。由图6可知：随b的增大，衬砌和塑性区切向应力σθ逐渐增大，塑性区切向应力峰值逐渐靠近塑性区内边界。考虑中间主应力的作用可以更加充分发挥材料的强度潜能，工程实践中要考虑中间主应力的对围岩的作用。

图5　kd/kc=50时b与R2的关系Fig.5　Relation between band R2 when kd/kc=50

图6　kd/kc=50和n=4时b与σθ的关系Fig.6　Relation between b and σθ when kd/kc=50 and n=4

3.3　脆性参数n对隧洞的影响

由图3和5知，随着脆性参数n的增大，塑性区半径均有不同程度的增加，如b=0.5和kd/kc=50时，n=8对应的塑性区半径R2比n=4所对应的R2增大了15.0%；从图7可知：随脆性系数n的增大，衬砌切向应力σθ不受脆性强弱的影响，塑性区内边界切向应力逐渐减小，塑性区切向应力σθ也逐渐减小且应力峰值逐渐远离塑性区内边界。可见考虑脆性损伤后，隧洞塑性区范围会有很大程度的增大，如不考虑损伤，计算结果会偏于保守。

图7　b=0.5和kd/kc=50时n与σθ的关系Fig.7　Relation between n and σθ when b=0.5, kd/kc=50

4　隧洞支护结构设计

前面的理论分析表明，围岩与衬砌渗透比、中间主应力系数、扩容系数、脆性参数等对塑性范围和应力都有一定的影响。在工程实践中，合理减少围岩与衬砌渗透比可大大减少塑性范围，降低衬砌应力，有利于减少衬砌厚度和配筋量，提高隧洞围岩的稳定性。

根据渗流量的变化可衡量围岩渗透性的变化，渗流量计算公式为[14]：

(24)

式中：q为隧洞每天每米排水量，m3/(m·d)；ha为保持渗流场稳定外水头与原渗流场一致水头，m，一般取值为100 m；其他符号含义同前。

对于本文所假设的算例，取衬砌混凝土渗透系数与围岩渗透系数相等为kd=5.0×10-6m/s，即kd/kc=1，将各参数代入式(24)可得q=120.04 m3/(m·d)。由文献[12]可知，为了保证隧洞的稳定性和安全，隧洞允许排放量控制在1～10 m3/(m·d)左右，相比较而言，算例计算结果远远大于隧洞最大允许控制量，显然不能满足要求。

对于具体水工隧洞，采用注浆加固圈来减小围岩渗透性，注浆圈的半径及渗透性应根据隧洞最大排水量和混凝土的的渗透性来具体分析。若认为混凝土不透水，则渗流量计算式为：

(25)

式中：kg为注浆圈的渗透系数，Rg为注浆圈外半径，其他符号含义同前。

对于本文所假设的算例，取衬砌混凝土渗透系数与围岩渗透系数相等，衬砌内半径为2.5 m，外半径为2.8 m；注浆圈内半径为2.8 m，外半径为3.6 m，渗透系数为围岩渗透系数的150倍。将各参数代入式(25)计算可得q′=6.852 m3/(m·d)，渗流量比前文计算结果大大的减小，可见堵水效果很好，围岩渗透性大大的降低，在衬砌渗透系数不变的情况下，由图2，3可知塑性半径和衬砌应力会大大的减小。

4　结论

1)本文基于统一强度理论和非线性损伤本构模型，考虑围岩与衬砌渗透比kd/kc、中间主应力系数b和脆性参数n等综合影响，深入研究衬砌和隧洞周边力学特征及塑性区范围，提供了一种更为准确的隧洞弹塑性分析。

2)渗透比kd/kc对隧洞的力学特征有显著影响。随kd/kc的增大，塑性区半径R2逐渐增大，衬砌内边界初始切向应力σθ不受渗透比和渗流的影响，衬砌和塑性区内边界处σθ逐渐增大，塑性区σθ逐渐减小且峰值逐渐远离塑性区内边界。用渗流量的变化来表征围岩渗透性的变化，通过采用注浆加固圈降低渗流量，减小围岩渗透性，可很好地降低塑性范围和隧洞切向应力。

3)随中间主应力系数b的增大，塑性区半径R2逐渐减小，衬砌和塑性区切向应力σθ逐渐增大且塑性区应力峰值逐渐靠近塑性区内边界，考虑中间主应力可以更加充分发挥围岩的承载能力，减少衬砌的支护强度。

4)随着脆性强度n的增大，塑性区半径R2均有不同程度的增加，塑性区内边界和塑性区切向应力σθ逐渐减小且应力峰值逐渐远离塑性区内边界，衬砌应力不受脆性强弱的影响。考虑脆性损伤后，隧洞塑性区会有一定程度的增大，如不考虑损伤，计算结果会偏于保守。

[1]徐芝纶．弹性力学(第二版)[M]. 北京: 高等教育出版社, 1982, 85-91.

[2]温森，杨圣奇．基于Hoek-Brown准则的隧洞围岩变形研究[J]．岩土力学，2011，32(1)：63-69．

WEN Sen, YANG Shengqi. Study of deformations of surrounding rock of tunnel based on Hoek-Brown criterion[J]. Rock and Soil Mechanics, 2011, 32(1): 63-69.

[3]卞康，肖明，刘会波．考虑脆性损伤和渗流的圆形水工隧洞解析解[J]．岩土力学，2012，33(1)：209-219．

BIAN Kang, XIAO Ming, LIU Huibo. Analytical solutions of circular hydraulic tunnel considering brittle damage and seepage[J]. Rock and Soil Mechanics, 2012, 33(1): 209-219.

[4]赵光明，张小波，孟祥瑞，等．基于连续损伤理论的巷道围岩弹脆性损伤分析[J].地下空间与工程学报，2016，12(2)：314-321．

ZHAO Guangming, ZHANG Xiaobo, MENG Xiangrui, et al. Elasto-brittle damage analysis of roadway surrounding rock based on continuous damage theory[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(2): 314-321.

[5]李宗利，任青文，王亚红．考虑渗流场影响深埋圆形隧洞的弹塑性解[J]．岩石力学与工程学报，2004，23(8)：1291-1295．

LI Zongli, REN Qingwen, WANG Yahong. Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291-1295.

[6]李忠华，潘一山．有渗流作用的油井井壁稳定性分析[J] ．工程力学，2002，19(3)：105-108．

LI Zhonghua, PAN Yishan. Stability analysis of well bore with permeation[J]. Engineering Mechanics, 2002, 19(3): 105-108.

[7]张常光，张庆贺，赵均海．考虑应变软化、剪胀和渗流的水工隧洞解析解[J]．岩土工程学报，2009，31(12)：1941-1946．

ZHANG Changguang, ZHANG Qinghe, ZHAO Junhai. Analytical solutions of hydraulic tunnels considering strain softening, shear dilation and seepage[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12):1941-1946.

[8]孟龙，高召宁，孟祥瑞．考虑损伤的圆形巷道围岩弹塑性分析[J]．中国安全科学生产技术，2013，9(11)：11-16．

MENG Long, GAO Zhaoning, MENG Xiangrui. Elasto-plastic analysis of circular roadway surrounding rocks under consider ation of rock damage[J]. Journal of Safety Science and Technology, 2013, 9(11): 11-16.

[9]荣传新，程桦．地下水渗流对巷道围岩稳定性影响的理论解[J]．岩石力学与工程学报，2004，23(5)：741-744．

RONG Chuanxin, CHENG Hua. Stability analysis of rocks around tunnel with ground water permeation[J].Chinese Journal of Rock Mechanics and Engineering,2004, 23(5): 741-744.

[10]周维垣，剡公瑞，杨若琼．岩体弹脆性损伤本构模型及工程应用[J]．岩土工程学报，1998，20(5)：54-57．

ZHOU Weiyuan, YAN Gongrui, YANG Ruoqiong. Elasto-brittle damage model for rock mass based on field tests in Laxiwa arch dam site[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(5): 54-57.

[11]任青文，邱颖．具有衬砌圆形隧洞的弹塑性解[J]．工程力学， 2005，22(2)：212-217．

REN Qingwen, QIU Ying. Elastic-plastic solution of circular tunnel with liner[J].Engineering Mechanics, 2005, 22(2):212-217.

[12]王秀英，王梦恕，张弥．山岭隧道堵水限排衬砌外水压力研究[J]．岩土工程学报，2005, 27(1)：125-127．

WANG Xiuying, WANG Mengshu, ZHANG Mi. Research on regulating water pressure acting on mountain tunnels by blocking ground water and limiting discharge[J]. Chinese Journal of Geotechnical Eegineering, 2005, 27(1): 125-127.

[13]俞茂宏．双剪理论及其应用[M]. 北京：科学出版社，1998：15-16．

[14]蔡晓鸿，蔡勇平．水工压力隧洞结构应力计算[M]．北京：中国水利水电出版社，2004：123-128．

[15]余天庆，钱济成．损伤理论及应用[M]．北京：国防工业出版社，1993：46-50．

[16]杜欣，曾亚武，唐冬云．基于水下抽水试验的岩体渗透系数研究及应用[J].岩石力学与工程学报，2010，9(29)：3542-3548．

DU Xin, ZENG Yawu, TANG Dongyun. Research on permeability coefficient of rock mass based on underwater pumping test and its application [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 9(29): 3542-3548.