基于安全约束的客站晚点列车到发线分配优化

刘　伟，朱晓宁

(北京交通大学 交通运输学院，北京 100044)

数字出版日期： 2017-04-24

0　引言

安全是铁路运输的基本要求，是铁路一切工作的基础。铁路大型客站的咽喉区和到发线的应用十分复杂，车站在接发车作业时应满足安全约束、行车约束等。针对铁路运输安全，张殿业等[1]提出了铁路运输安全研究的框架体系；范振平等[2]分析了铁路运输生产中的不利因素，探讨了铁路安全预警系统的实现。在车站安全作业的要求下，车站到发线作为铁路客运站基础设施的关键资源和重要组成部分，在接、发车作业中发挥着不可替代的作用[3-6]。针对铁路车站到发线作业优化问题，国内外学者建立了相关数学优化模型，如Carey等[7]构建了到发线分配优化的混合整合规划模型；Zwaneveld等[8]采用点包装问题描述到发线运用问题，建立了0-1整数规划模型；Cardillo等[9]基于客运站的到发线分配优化，建立图染色模型。此外，Billionnet等[10]定义相容进路集，将车站到发线优化视为带有权重的点包装问题，构造了无向图，采用分支定界法求解。Li等[11]建立了铁路客站到发线选择的优化模型，将车站的作业能力作为约束条件，并使用K短路算法进行求解。D’Ariano等[12-13]通过模拟人工调度，针对复杂车站列车到发线运用调整问题设计相应启发式算法。

在保障列车进站作业安全的条件下，通过提高旅客列车的准点率，采取动态时刻表的方式，可优化车站作业，消除列车在站内的作业冲突，确保行车安全[14-15]。Huisman等[16]研究不确定列车运行图问题，考虑线路通过能力，根据防冲突的疏解原则建立了列车进出站模型；Burdet等[17]对车站能力进行评估，并设计随机贪婪搜索算法计算车站最大通过能力；Castillo等[18]和Corman等[19]基于列车运行图，优化列车进出站路径。

随着列控技术的发展，铁路技术装备水平的提升，铁路安全行车和准点率水平显著提高。然而，由于铁路运输网络的开放性和运输组织工作的复杂性，存在各种不确定因素的干扰，如车站设备故障、出现极端天气、区间线路损坏、节假日旅客集中进站上车和临客的大规模开行等，造成不同规模、不同程度的晚点，车站到发线分配又受制于各种安全条件约束，因而需要根据实际情况及时调整到发线使用，避免列车晚点传播。因此，基于安全约束对列车晚点情况下的到发线调整优化具有重要的实用价值。鉴于此，本文研究基于安全约束的客站晚点列车到发线分配优化。采用混合整数建模方法建立优化模型，设计模拟退火算法进行求解，并以宝鸡站为例进行案例分析。

1　基于安全约束的到发线分配优化模型

1.1　问题提出

如图1所示，正点情况下列车T3到达车站时刻t1，离开车站时刻t5，停留Ⅰ道；T1到达车站时刻t2，离开车站时刻t3，停留Ⅱ道；T2到达车站时刻t4，离开车站时刻t6，停留Ⅱ道。当列车T1晚点至t4到达，此时出现列车进站安全冲突，列车T1与T2在满足安全约束条件下的进站的先后次序，在实际接发车作业过程中是一个优化决策问题。此外，后进站列车T1(或T2)停留在Ⅰ道还是Ⅱ道(待T3离站)，也是一个决策优化。以上示例仅考虑两条到发线，一列车发生晚点的到发线优化调整问题。在实际作业中列车晚点时有发生，且当问题的规模逐渐扩大(到发线数、列车数、晚点车数)，同样需要满足安全条件约束，该组合优化问题的复杂度呈几何增长。为此，本文研究基于安全约束的客站晚点列车到发线分配优化，可为该问题提供科学的理论依据。

图1　铁路车站列车晚点示意Fig.1　Train delay in a railway station

1.2　数学模型

1.2.1模型假设

模型建立基于以下假设：不存在行车事故，站内设施设备均能正常使用；任意列车遍历咽喉区单个道岔占用时间已知；前后两列列车进入同一到发线的安全时间间隔为常量。

1.2.2集合符号定义

集合定义：车站道岔组集合D，任意道岔组d∈D，D={d|d=1,2,...,n}，其中n为道岔组总数；阶段计划内到发列车集合L，任意列车l∈L，L={l|l=1,2,...,m}，其中m为该阶段计划内的列车到发总数；车站到发线集合，任意到发线g∈G，G={g|g=1,2,...,r}，其中r为到发线总数。

1.2.3目标函数

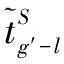
(1)

(2)

判断列车l晚点到达车站时，预设到发线g是否空闲。∀g,g′∈G,∀l∈L：

(3)

式(3)表示列车是否进入预设到发线。正点情况下列车l进入预设到发线g，当发生晚点后需判断到发线g是否空闲。若到发线g空闲则晚点列车l可进入该到发线；若到发线g繁忙则晚点列车需等待或另行分配。引入0～1变量αl，∀g,g′∈G,∀l∈L：

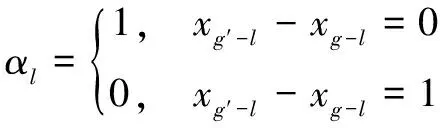
(4)

式(4)表示列车是否进入原到发线。当αl=1，则列车l进入预设到发线；反之，需另行分配到发线。

其次，判断该时刻是否有多列车同时到达，∀g,g′∈G,∀l∈L：

(5)

引入指标函数f(αl,βg)：

f(αl,βg)=αl+βg

(6)

式(6)表示对列车到发线分配的方案设置。根据f(αl,βg)大小，对车站列车出现晚点情况下的到发线再分配计划设阈值，根据阈值的大小，嵌入表1的操作。

表1　不同情况下的列车进站操作

针对有多列车同时进站，且其预设到发线相同的情况下，考虑列车权重系数wl。列车权重系数wl越大，安排其进入预设到发线的可能性越大。当出现表1中的情况2时，权重系数wl最大的列车进入到发线g，其余列车另行分配。当出现情况4时，根据不同列车的权重大小，逐一分配到发线。情况1和3由于只存在一列列车，因此，权重系数不必考虑。

对晚点情况下的列车进站咽喉利用和到发线分配，本文以列车二次延误时间最小化为目标，考虑各趟列车的权重大小，目标函数如公式(7)：

(7)

1.2.4模型约束条件

1)进站道岔组安全约束

(8)

2)停站到发线安全约束

(9)

式(9)表示到发线占用安全约束。为确保进站作业安全，1个时间段内，1条到发线只能接发1列列车。

3)进站列车必须安排到发线约束

(10)

式(10)表示必须给进站列车l安排一条到发线进行停站作业。

4)出站道岔组安全约束

(11)

5)防冲突安全约束

(12)

式(12)表示列车进站防冲突安全约束，一般而言列车进入到发线前要求到发线已清空。具体要求到发线的占用时段间需要有一段安全间隔时间，防止列车之间发生进、出站冲突。Tmin表示最小安全时间间隔。

2　模拟退火算法

客站咽喉利用与到发线分配优化问题是一类NP-hard问题，问题复杂度高且较难求解，本文采用基于模拟退火算法的启发式算法求解以上模型。模拟退火算法的解的表示与迭代如图2所示，解的横轴表示到发线号，纵轴表示列车。单一父代解产生子代解的方法：通过变异任一列车的停站到发线，并检查是否满足约束条件，决定是否保留该子代解。两个父代解产生子代解的方法：两个父代解通过交换某列车的停站到发线生成两个子代解，检查子代解是否满足约束，若满足则保留该子代解。通过比较上述解的优劣，选择性保留最优解作为下一次迭代的开始。

具体求解步骤如下：

第1步，初始化。

1)初始输入。初始温度值T0，算法停止温度τ，降温系数ω以及马尔科夫链长度L为算法的初始输入值。

2)基础数据读取。读取车站咽喉结构，输入咽喉道岔组占用时间以及安全间隔时间ΔT、Tmin，列车的时刻及晚点时间。

3)产生初始解。初始化当前温度T=T0，随机产生初始解s0，计算目标函数值f(0)，检查约束条件公式(8)～(12)，若满足条件保留该初始解，如果不满足通过交叉产生新解，直至满足约束条件。

图2　模拟退火算法解的表示Fig.2　Solution expressions of the simulated annealing algorithm

图3　宝鸡车站站场示意Fig.3　Map of the station bottleneck structure (Baoji, China)

第2步，迭代优化。

1)产生新解。初始解通过交换某列车的停站到发线生成一个新的子代解，两个父代解通过交换某列列车的停站到发线产生两个新子代解sn

2)新解判断。判断以上子代解是否满足约束条件(8)～(12)，并计算满足约束条件解的目标函数值f(η)，计算当前解与前解的目标函数之差Δf，Δf=f(η)-f(η-1)。若Δf≤0，则sn替换sn-1，否则采用随机概率事件让sn替换sn-1，概率为ρ=exp(-Δf/T)。

3)迭代终止判断。对于当前温度T，如果T≤τ，停止；否则更新T=T×ω，继续进行下一次迭代。

3　实例研究

为了测试模型与算法的有效性，选取宝鸡车站作为案例进行研究与分析。图3为宝鸡站站场示意图，其中到发线11条(股道VII，VIII号为正线)，道岔组28组。宝鸡车站分为左右两侧咽喉，左侧咽喉由奇数号道岔组构成(1-3-5-…-25)，右侧咽喉由偶数号道岔组构成(2-4-6-…-28)，表2为列车时刻表相关信息。

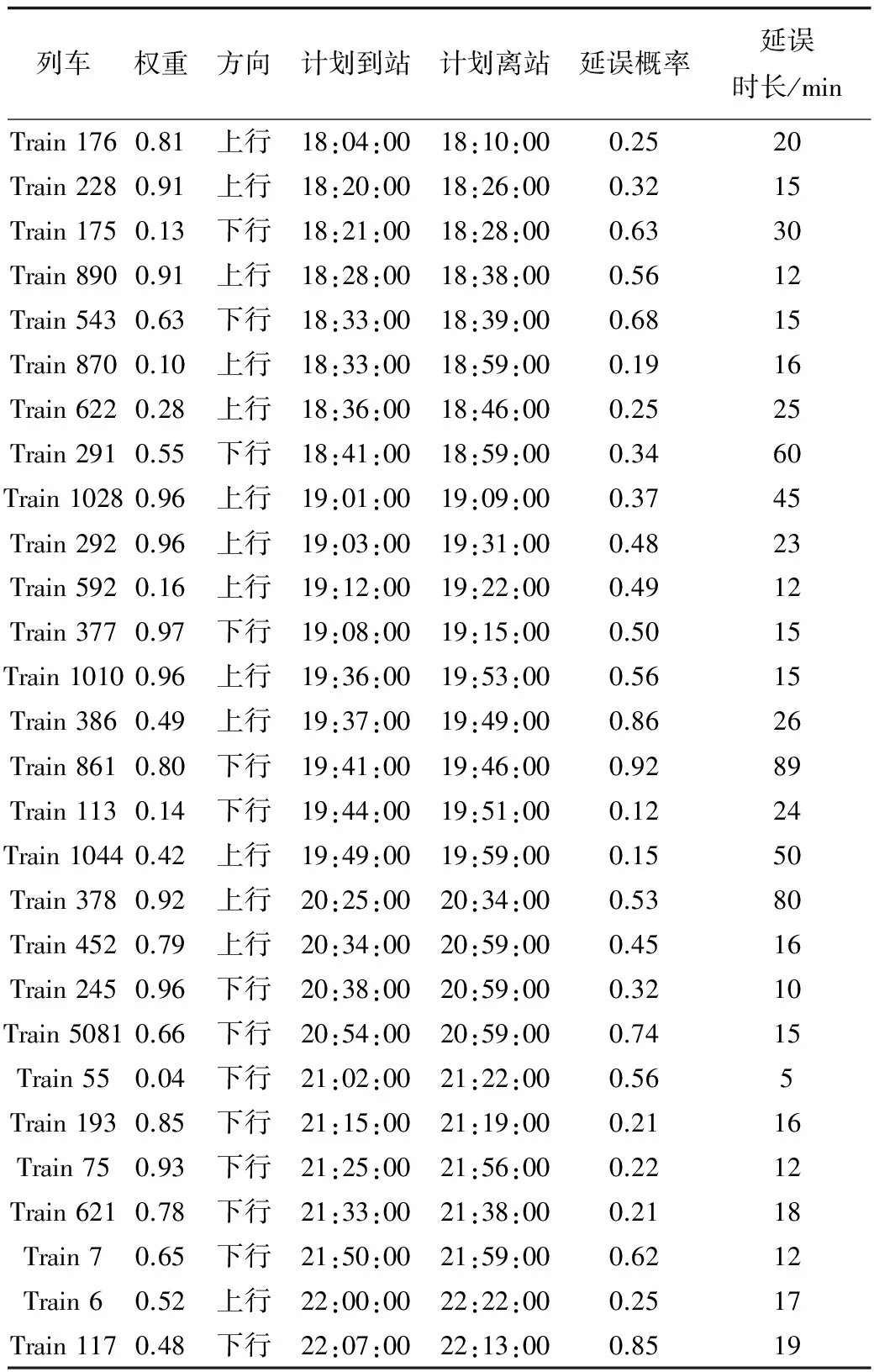
表2　宝鸡车站部分列车初始时刻

注：由于缺乏实际的列车延误数据，本表采用正态分布模拟了列车延误概率及时长。

3.1　延误处理

为表示列车是否延误，采用延误概率计算。本文假设列车的延误概率成正态分布，如表2所示，设为该列车的延误概率。

(γl-1)·M≤(δl-Xl)≤γl·M

(13)

式(13)表示延误列车。其中，M为极大整数；γl为0-1变量，表示列车l是否按延误处理。若γl=1，则按延误处理；若γl=0则按正点处理。当延误概率δl大于等于阈值Xl时，γl=1；否则，γl=0。

εl′=εl·γl

(14)

式(14)表示列车延误时长。εl为列车的预设延误时长，根据延误概率计算列车的延误时长εl′。

3.2　优化结果

取Xl为0.5，对表3中列车延误概率及延误时长进行统计，延误列车数12列，延误总时长333 min。到发线的占用频次分别为[2 1 3 3 2 2 2 5 3 3 2]，其中，到发线8占用频次最高，为5次；到发线2占用频次最低，为1次；其余各条到发线均占用2到3次不等。

表3　列车延误后到发线分配及道岔组组成优化结果

3.3　延误时长分析

改变列车延误总时长，分析列车延误时长对车站到发线分配的影响。将列车延误数量逐一叠加，产生变化的延误总时长。根据宝鸡车站的列车运行时刻表，假设列车延误数量是离散变量，变量值范围为1～7，统计相应的延误时间，分别从30～202 min，优化后的结果见表4。发现随着列车延误总时长的增加，列车的二次延误时长呈(准)对数函数递增。

表4　列车延误总时长分析

3.4　延误时长与延误车数热力分析

列车调度优化中准点率是一个非常重要的指标。随着延误列车数量的递增(如受到延误传播的影响)，二次延误时长势必增加。造成列车二次延误的原因除了受车站资源有限影响，也跟列车晚点时长相关。因此，分析延误列车数量与列车延误时长之间的热力关系，能够给调度工作者一定的科学指导。在此，假定列车延误数量按线性增加，即1到N；各次列车的延误时长亦呈线性递增关系，即5到t′ min。

图4　列车延误数量与延误时长对二次延误的影响Fig.4　Influence of the number of delayed trains and delay times on the second-delay times

测试以上实验数据，得到图4和表5所示结果。发现当列车延误时长较短时(如2 min)，随着延误车数的增加，列车二次延误时间递增较缓慢。该结果说明宝鸡车站的列车到达间隔时间预留较合理，满足车站接发车安排作业的鲁棒性特征。当列车延误时长增加至10 min时，延误车数的影响逐渐凸显。而当列车延误时长突增至24 min时，只需几列列车延误，便会造成长时间的二次延误。以上结论说明，调度在安排列车晚点情况下的到发线分配作业时，首先建议考虑列车的延误时长，当延误时长较长时，需要优先解决延误车数问题，即优先安排非延误列车的进站作业；当延误时长在可控范围内，可以遵循“先到先服务”(First-in-first-service)原则，逐一安排到站列车完成到、发作业。

表5　二次延误时长

4　结论

1)建立了列车到发线分配优化混合整数规划模型，设计了模拟退火算法求解该大规模NP-hard问题。

2)以宝鸡车站案例分析表明，当列车晚点时间较短情况下，列车依次进站作业一般能满足安全约束，可采取“先到先服务”原则，当有多列列车晚点且时间较长时，在满足安全约束条件下，优先安排非晚点列车进站作业才能有效避免晚点传播。

[1]张殿业, 金键, 杨京帅. 铁路运输安全理论与技术体系[J]. 中国铁道科学,2005(5):114-118.

ZHANG Dianye, JIN jian, YANG Jingshuai. Railway transportation safety theory and technology system[J], China Railway Science, 2005(5):114-118.

[2]范振平, 林柏梁, 李俊卫.铁路局安全预警系统的研究[J].交通运输系统工程与信息,2006(12):149-152.

FAN Zhenping, LIN Boliang, LI Junwei. Study on security early warning system of railroad bureau[J]. Journal of Transportation Systems Engineering and Information Technology, 2006(12):149-152.

[3]Kang L J, Wu J J, Sun H J. Using simulated annealing in a bottleneck optimization model at railway stations. Journal of Transportation Engineering [J]. 2012, 138: 1396-1402.

[4]张嘉敏, 韩宝明. 铁路列车占用车站股道时序优化研究[J]. 交通运输系统工程与信息, 2011,11(3): 100-107.

ZHANG Jianmin, HAN Baoming. Optimization on the occupation order for trains on tracks of the railway station[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(3): 100-107.

[5]青学江,马国忠.遗传算法在区段站到发线的应用研究[J]. 西南交通大学学报, 1998(4): 387-393.

QING Xuejiang. MA Guozhong. Application of GA to arrival and departure lines in district stations[J]. Journal of Southwest Jiaotong University, 1998(4): 387-393.

[6]雷定猷, 王栋, 刘明翔. 客运站股道运用优化模型及算法[J]. 交通运输工程学报, 2007(5):84-87.

LEI Dingyou, WANG Dong, LIU Mingxiang. Optimization model and algorithm of utilization of arrival and departure tracks in railroad passenger station [J]. Journal of Traffic and Transportation Engineering, 2007(5): 84-87.

[7]Carey M. A model and strategy for train pathing with choice of lines, platforms, and routes [J]. Transportation Research Part B Methodological, 1994, 28(5):333-353.

[8]Zwaneveld P J, Ambergen H W. Routing trains through railway stations: Model Formulation and Algorithms [J]. Transportation Science, 1996, 30(3):181-194.

[9]Cardillo D D L, Mione N. k L-list colouring of graphs [J]. European Journal of Operational Research, 1998, 106(1):160-164.

[10]Billionnet A. Using integer programming to solve the train-platforming problem [J]. Transportation Science, 2003, 37(2):213-222.

[11]Li Y, Zhao J, Cheng J. Model and algorithm for passenger station task allocation problem in railway terminal [J]. Journal of Transportation Engineering, 2010, 2590-2596.

[12]D’Ariano A, Dario, P. Assessment of flexible timetables in real-time traffic management of a railway bottleneck [J]. Transportation Research Part C. 2008, 16:232-245.

[13]Andrea DA, Dario P. Assessment of flexible timetables in real time traffic management of a railway bottleneck [J]. Transportation Research Part C, 2008, 16: 232-245.

[14]Delorme X, Gandibleux X, Rodriguez J. GRASP for set packing problems [J]. European Journal of Operational Research, 2004, 153(3): 564-580.

[15]Zwaneveld P J, Kroon LG, Hoesel S P M V. Routing trains through a railway station based on a node packing model [J]. European Journal of Operational Research, 2001, 128(1):14-33.

[16]Huisman T, Boucherie R J. Running times on railway sections with heterogeneous train traffic [J]. Transportation Research Part B, 2001, 35 (3): 271-292.

[17]Burdet T R L, Kozan E. A disjunctive graph model and framework for constructing new train schedules [J]. European Journal of Operation Research, 2010, 200(1):85-98.

[18]Castillo E, Gallego I, Uuena G J, Time tabling optimization of a mixed double and single tracked railway network [J]. Applied Mathematical Modeling, 2011, 35(2):859-878.

[19]Corman F, Dariano A, Pacciarelli D. A tabu search algorithm for rerouting trains during rail operations [J]. Transportation Research Part B: Methodological, 2010, 44(1):175-192.