求解模糊线性系统的Jacobi迭代法

顾 颖, 陈 新

(1.宿迁学院 文理学院, 江苏 宿迁 223800; 2.南京师范大学 数学科学学院, 江苏 南京 210046)

求解模糊线性系统的Jacobi迭代法

顾 颖1, 陈 新2

(1.宿迁学院 文理学院, 江苏 宿迁 223800; 2.南京师范大学 数学科学学院, 江苏 南京 210046)

给出了求解模糊线性系统的基于矩阵方程模型的Jacobi迭代法,并用实例说明方法的有效性.

模糊线性系统; 迭代解法; Jacobi方法

0 引言

模糊线性系统在工程分析,自动控制,经济金融等领域发挥着越来越重要的作用,因此研究它的求解变得十分的必要和迫切.Friedman首先提出了一个求解n×n阶模糊线性系统的一般模型[1],该模型的系数矩阵由精确数构成,但右端是由模糊数构成的向量,后人以此模型为基础,相继提出了求解模糊线性系统的一类迭代法,诸如Jacobi迭代法,Gauss-Seidel迭代法,SOR迭代法[2]等方法,在这些方法中始终无法避免模糊数的出现.Feng在Friedman的模型的基础上作进一步提炼,将问题转化为求解矩阵方程[3],在新的模型中,完全避开了模糊数,这就给模糊线性系统的求解开辟了新的思路.本文中,我们将把求解矩阵方程的Jaboci迭代法用到新模型上,得到求解模糊线性系统的基于矩阵方程模型的Jacobi迭代法,并用实例说明算法的有效性.

1 预备知识

考虑n×n阶模糊线性系统

(1)

则称模糊数向量x=(x1,x2,…,xn)T为模糊线性系统的一个解.

依据Friedman的理论,由定义1,模糊线性系统(1)可转化为为2n×2n阶线性方程组:

Sx=y

(2)

或

攀枝花钛精矿经过改性- 酸浸后，所得产品人造金红石中CaO含量、SiO2含量去除率低下的原因主要受钛精矿物相组成决定。攀枝花钛精矿主要由易溶的钛铁矿和难溶的硅酸盐两种物相组成，其中大部分为钛铁矿相。杂质元素Mg既分布在钛铁矿中，也分布在硅酸盐相中，而Ca和SiO2主要分布在硅酸盐相中。钛精矿中SiO2越多，硅酸盐相存在越多，CaO则越难被浸出[8]。攀枝花钛精矿中SiO2含量达到了4%左右，在制取人造金红石过程中，只能除去部分CaO，采用磁选的方式也只能部分去除SiO2和CaO。图1为攀枝花钛精矿物相组成。

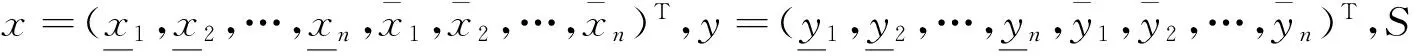
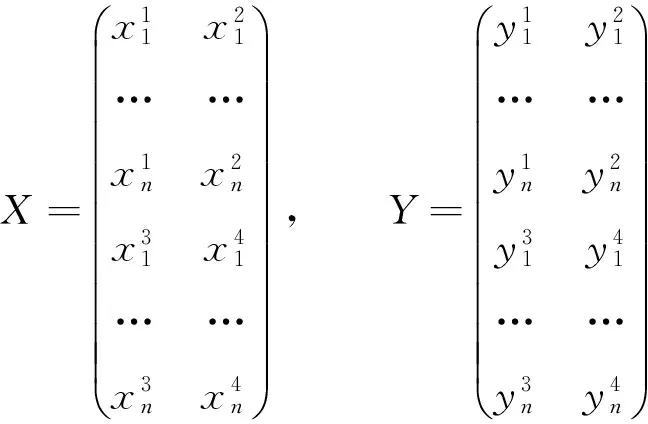
则Sx=y可表示为矩阵方程

SX=Y

(3)

其中S为2n×2n阶系数矩阵,X为2n×2阶未知矩阵,Y为2n×2阶已知矩阵.在第2部分,将以Feng的矩阵方程模型(3)为基础,构建本文中的主要方法.

2 主要结果

对于形如AX=B的一般矩阵方程,蔺小林等人给出了求解它的Jacobi迭代法[4].上一部分中所得的矩阵方程模型SX=Y为它的一种特例,因此,可将此迭代法应用于矩阵方程(3),得到求解模糊线性系统(1)的基于矩阵方程模型的Jacobi迭代法.现将该方法总结如下:

对SX=Y的系数矩阵S作如下分裂S=-L+D-U其中

其中D为非奇异对角阵,L和U分别为主对角线元素为0的下三角阵和上三角阵.

根据蔺小林等人提出的解一般矩阵方程AX=B的Jacobi迭代法[4]的原理,先将矩阵方程(3)改写为如下等价形式:

任取2n×2阶初始迭代矩阵X(0)代入上述等价形式,可得迭代格式

(4)

该式若写成矩阵形式,则由式(4)得

DX(k+1)=(L+U)X(k)+Y,

故

X(k+1)=D-1(L+U)X(k)+D-1Y

(5)

式(4)或(5)即为求解模糊线性系统(1)的基于矩阵方程模型的Jacobi迭代法的迭代格式.通过迭代,求出矩阵方程SX=Y的2n×2阶解矩阵X,再利用模糊数的特点,表示出模糊线性系统(1)的解.

3 数值例子

例1 考虑3×3阶模糊线性系统

则

取初始迭代矩阵X(0)为6×2阶零矩阵代入Jacobi迭代格式(4),经3步迭代,得矩阵方程(3)的近似解

再结合模糊数的特点,从而得到模糊线性系统的近似解为

事实上,此解为该模糊线性系统的精确解.在整个计算过程中没有涉及到参数r,而朱莉用SSOR-CG方法解本例的计算结果是当参数r取[0,1]中的11个点处的离散值[5].对比之下,可见本文提供的方法有其优越性.

[1] Friedman M, Ma M. Fuzzy linear systems[J]. Fuzzy Sets Syst,1998(96):201-209.

[2] Allahviranloo T. Numerical methods for fuzzy systems of linear equations[J]. Applied Mathematics and Computation, 2004,155(1):493-502.

[3] Feng Y. An iterative method for fuzzy linear systems[J].Fifth Interational conference on Fuzzy Systems and Knowledge Discovery, 2008,1(1):565-569.

[4] 蔺小林,霍佩佩.线性矩阵方程的迭代求解方法[J].陕西科技大学学报,2015, 33(1): 175-178.

[5] 朱莉.解模糊线性方程组的SSOR-CG方法[J].科技信息,2009, 28(1): 103-104.

[责任编辑：李春红]

Jacobi Iterative Method for Solving Fuzzy Linear Systems

GU Ying1, CHEN Xin2

(1.School of Arts and Science, Suqian College, Suqian Jiangsu 223800, China (2.School of Mathematical Science, Nanjing Normal University, Nanjing Jiangsu 210046, China)

The Jacobi iterative method based on matrix equation model for solving fuzzy linear systems is presented, and the effectiveness of the method is illustrated by an example.

fuzzy linear systems; iterative method; Jacobi method

2017-01-05

国家自然科学基金资助项目(11271196); 江苏省教育厅自然科学研究资助项目(07KJD110094)

顾颖(1986-),女,江苏宿迁人,讲师,硕士,研究方向为数值代数. E-mail: guying-1986@126.com

O241

A

1671-6876(2017)01-0010-04