新高考背景下高中非毕业年级数学命题策略研究
2017-04-14赵爽
赵爽
[摘 要] 笔者任教于重庆市南开中学高中部,关注到校内甚至全市对“适应全国卷新高考”的教学和复习备考策略的研究氛围浓厚,但对非毕业年级的关注和研究较少,尤其是对非毕业年级同步教学命题工作的应对策略研究很少. 本文将通过全国卷数学学科在试题结构、考点分布、考题难度等方面的特点,对比并总结出相关变化,提出非毕业年级在同步教学命题工作中的应对策略,以期对正在高一、高二年级任教的数学教师在同步教学命题和适应全国卷的教学上提供些许帮助.
[关键词] 新高考;全国卷;非毕业年级;命题特点;应对策略
[?] 研究背景
2014年9月4日,国务院颁布了《关于深化考试招生制度改革的实施意见》,明确指出,深化高考考试内容的改革,2015年起增加使用全国统一命题试卷的省份. 从2016年开始,重庆高考采用全国卷已毫无悬念,而全国卷和重庆卷不管是在试卷结构方面还是在从考试范围与内容方面,考试的主干内容侧重点与位置摆放方面以及更深入一点的试卷梯度、区分度方面都有着明显的不同. 在这种背景下,研究新形势下高中数学教学和命题的应对策略就显得很有必要了.
现在大多数关于新高考全国卷命题和备考复习工作的研究,都是针对毕业年级的,对非毕业年级的教学、备考、命题研究却为数不多. 从长远来看,适应全国卷命题的工作应该尽早开展,在高一、高二的教学、命题、评价等教学环节中都应尽早地适应全国卷的评价标准,使教师的教学工作更有的放矢,使学生的学习过程更有益于能力的提高.
[?] 新高考数学全国卷的命题特点简析
1. 结构变化,立足基础,考查全面
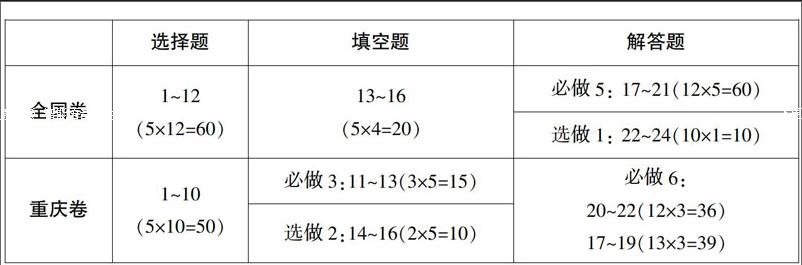
首先是各题型试题数目和分值的变化,值得关注的是对选修内容的考核. 由重庆卷填空题三选二,变为全国卷的解答题三选一,由题型变化和题数变化带来了难度的变化. 整体来看,全国卷对选修内容的考核难度较之重庆卷有所提升,但基础知识的比重仍是最大,且基础知识中尤其重视通式通法的考查. 相比于重庆卷,全国卷中等难度问题会更多一些,难题和简单题都会少一些,让更多的学生能做到所有试题,更全面地考查学生的知识和能力.
2. 内容变化,突出主干、重视通法,注重思维能力的考核
相较重庆卷,全国卷有一些“新增”内容:三角恒等变换中积化和差、和差化积、半角公式等,曲线与方程,统计案例中的独立性检验、正态分布、线性回归方程,定积分与微积分基本定理,选修系列4不等式的证明等,这些都是重庆卷不考的内容或者边缘的内容,但却已经多次出现在新课标全国卷的内容中. 此外,笔者还关注到,统计学的独立性检验、线性回归方程、正太分布越来越多地出现在全国卷的考题中,多以实际问题为背景. 如2015年新课标Ⅱ卷第18题考查了茎叶图和独立性检验,2014年新课标Ⅱ卷和2015年新课标Ⅰ卷第19题均考查了线性回归方程,2014年新课标Ⅰ卷第18题考查了正态分布. 数学应用越来越受到命题组的青睐.
另外,解答题部分,全国卷在题目考核知识点上也具有一定的稳定性,通过对比能够看出,变化主要体现在数列、函数与导数、选修内容的考法上. 其中全国卷数列问题主要考查数列的性质、通项与前n项和,通常位于第一个解答题,难度较低;而重庆卷主要考查数列不等式,通常位于压轴题的位置,对学生的综合能力要求颇高,难度大不易得分. 全国卷的压轴题多以函数导数内容为主,主要涉及恒成立、参数问题、最值问题和不等式问题,题目条件简洁常规,虽有难度但相对较易入手;而重庆现行高考中通常将函数导数问题设置为中等难度的解答题,不作为压轴题出现.
3. 稳中求新,思辨性强,重视迁移能力的考查
全国卷立足课标,考点相对稳定,但载体时常革新,经常在高中数学知识模块交汇处,在中学数学与高等数学交汇处设计问题,以競赛数学思想或改编竞赛题的情境命制高考题目,考查教材中出现过的高等数学思想、数学文化,用创新形式的方式实现迁移能力的考查. 而在竞赛背景下和高等数学背景下设计的题目往往具有极强的思辨性,需要学生在数学思想的高度寻求解题突破口,充分考查学生的数学学习能力和问题解决能力.
例:(2013年新课标Ⅰ卷12题)设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n∈N*,若b1>c1,b1+c1=2a1,an+1=an,bn+1=,cn+1=,则( )
A. {Sn}为递减数列
B. {Sn}为递增数列
C. {S2n-1}为递增数列,{S2n}为递减数列
D. {S2n-1}为递减数列,{S2n}为递增数列
答案:B. 本题在数列知识和解析几何知识交汇处设题,体现由数到形的转化、抽象到具象的转化,着重考查数形结合、极限、转化与化归等数学思想方法以及分析问题、解决问题的能力和创新能力,是该套高考试卷的一个亮点.
[?] 非毕业年级试题命制的应对策略
非毕业年级的教学工作要立足新高考对学生知识和能力的要求,在教学过程中贯彻落实教材中渗透的基础知识技能、数学思想方法、数学思维能力、数学文化素养,并在命题中充分设计考点考题,最大限度地拟合高考命题的特点,达到多方位立体检测知识和能力的目的.
1. 结构对接,基础知识和基本技能重点考查
首先,试题的结构是决定学生考试时间分配的关键,所以在同步教学试题命制时,教师应有意识地按照高考试卷的结构命题,即按照12道选择题、4道填空题、6道解答题的题量、题型设定,以保证学生适应跟高考相似的考试模式. 另外,同高考命题指导思想一致,同步章节的命题也要重视对阶段内基础知识、基本技能、基本思想方法的考查,在主观题、客观题上始终按照先易后难的顺序进行排列,便于学生在考试时能顺利地进入状态并稳定发挥. 值得关注的是,高考全国卷最后的第22题、第23题、第24题均是分值为10分的选做题,学生需择其一而答,内容为选修新增的内容,考核难度较低. 那么,在学生学习这些知识前,非毕业年级无法直接以三选一的形式仿真考查,这时我们可以模拟高考中该类问题的难度,设计一道较为基础的解答题(笔者所在学校即把第17题设定成为10分的题目),用以考查阶段内最基础的主干内容.
近年来,高考试卷中基础题、中档题、难题的分值比例基本稳定在6∶3∶1,因此,对非毕业年级试题的命制也要按这一比例分配各梯度层次的题目. 在基础知识和基本技能的考核题目中,要依据高考的标准,注重通式通法,淡化特殊技巧,回避重复、繁杂的机械运算.
2. 选题有道,适应全国卷能力立意的指导思想
遵循命题的公平性原则,一次重要的考试,不该使用成卷或成题,因此要求命题者改编或原创出符合命题要求的各类型试题.
(1)立足基础,回归教材,提高试题辐射广度,严控试卷绝对难度.
试卷中避免成题是为了确保试题的公平性,但教材中的例题和课后配备的习题和拓展资料对每个考生而言都是公平的. 笔者在实际教学过程中发现,很多学生对数学教材的重视度不够,部分教师对教材渗透的潜在知识和思想挖掘不深,导致教材未能发挥最大作用. 然而,纵观近3年全国卷的高考试题,总会发现取材课本的案例. 因此,笔者认为,适应新高考,首要的任务是适应新高考“立足基础,回归教材”的指导思想. 选编课本原题,仿制课本例题,生成课本变题,一方面能保证大部分考生获得基本分数,另一方面也能引导师生吃透教材、深研教材. 但改编教材题目作为考试题目要注意:题目要具有典型性,同套试卷中数量不宜过多,以免导致学生“死记硬背”的应对策略. 选用教材题目或素材,是为了让学生在熟悉的题境中解决问题,但不代表这类题目是苍白的送分题,可以通过合适的设计让学生感受到题目的“数学味”,常用的方法有:改变题型、数据、图形、情境、背景,对已有结论进行推广延伸,跨章节素材整合等.
原题:(人教版必修1第83页B组第4题)设f(x)=,g(x)=.
求证:(1)[g(x)]2-[f(x)]2=1;
(2)f(2x)=2f(x)·g(x);
(3)g(2x)=[g(x)]2+[f(x)]2.
改编1:设f(x)=,g(x)=,给出如下结论:
①对任意x∈R,有[g(x)]2-[f(x)]2=1;②存在实数x0,使得f(2x0)>2f(x0)·g(x0);③不存在实数x0,使g(2x0)<[g(x0)]2+[f(x0)]2;④对任意x∈R,有f(-x)g(-x)+f(x)g(x)=0.
其中所有正确结论的序号是________. (答案:①③④)
改编2:已知函数F(x)=ex满足F(x)=g(x)+h(x),且g(x),h(x)分别是R上的偶函数和奇函数,若?x∈[1,2],有不等式g(2x)-ah(x)≥0恒成立,则实数a的取值范围是________. (答案:a≤2)
改编3:已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ex,则=______________ . (答案:)
(2)创新情境,适度综合,注重数学思想和数学文化的考查.
适应全国卷的高考数学命题,尤其要适应以一定程度的综合性、创新性为表征的数学思想和数学文化的考查要求,这二者着重考查学生的问题解决能力、数学抽象能力等数学学习能力,难以一蹴而就,最好让非毕业年级就开始适应这样的题目和考法.
这就要求非毕业年级的命题者在选题、编题、创题的过程中更注重设计题目的潜在考点和深层立意,用高考常用的命题方法指导同步教学的命题,如在知识交汇处命题,以数学史料、数学文化为背景命题,在实际背景下编制数学应用问题,甚至将高考真题和模拟题进行改编或仿真原创,充分体现考查数学思想、数学文化的命题原则.
但對于非毕业年级的命题而言,编制此类试题的综合度不宜过高,数量不宜过多,以当下学习时段内的知识为主干,适当地进行知识迁移或拔高拓展即可. 适合编制部分中等难度的主、客观题目和较难的压轴题目,中档题要让多数学生有发挥和探究的空间和时间,压轴题目也要通过题设条件和背景的设计,给学生以适度提示. 像全国卷的压轴题一样,起点很高但落点很低,让能力稍差的学生因不陌生而产生勇气,让能力强的学生因深入探究而感受到隐藏的价值和深意.
如下几道题目,均是高一年级所学知识,在数列和平面向量三点共线知识的交汇处设题,随着题设条件的改变,综合度和难度截然不同. 试题1考查等差数列的性质、等差数列的前n项和公式和三点共线系数和为1,比较容易,适合设置在第7或第8题;试题2考查数列递推公式求通项、等比数列前n项和公式、分组求和法、三点共线系数和为1,适合设置在第14或第15题;试题3考查数列递推、周期数列、并项求和法、三点共线系数和为1,其中周期的推导和发现较难,适合设置在第15或第16题;试题4考查数列递推、裂项求和、数列单调性、三点共线系数和为1,其中对递推公式进行裂项是难点,适合设置在第16题.
试题1:已知{an}为等差数列,Sn为数列{an}的前n项和,平面内三个不共线的向量,,,满足=(a17-2)+a2000,若点A,B,C在同一条直线上,则S2016=( )(答案:A)
A. 3024 B. 2016
C. 1008 D. 504
试题2:Sn为数列{an}的前n项和,a1=1,平面内三个不共线向量,,,满足=an+1-2an(n∈N*),若点A,B,C在一条直线上,则Sn=_________.(答案:2n+1-n-2)
试题3:Sn为数列{an}的前n项和,a1=a2=1,平面内三个不共线向量,,,满足=(an+1+an-1)+(1-an)(n≥2,n∈N*),若点A,B,C在一条直线上,则S2018=________.(答案:2)
试题4:数列{an}与平面内三个不共线向量,,满足=-an,a1=1,Sn为数列
的前n项和,用[x]表示不超过x的最大整数,则当三点A,B,C 在一条直线上时,[S2016]=( ) (答案:A)
A. 0 B. 1 C. 2 D. 3
(3)高观点立题,能力立意,在高等数学背景下设题.
针对高考中频繁出现的基于竞赛和高等数学背景的题目,这些题目往往难度较大或形式新颖,对学生综合能力的要求高,需要从起始年级开始接触和适应这种立足高观点的试题. 事实上,高中的很多概念都是高等数学知识的下放,命题者可以在这些概念上做文章命制题目,也可以借助高等数学或数学史中的著名问题命制题目,甚至可以尝试编制一些能用高等数学中的初等方法来解决的问题作为考试题目.
但这一命题方法要求命题者具有较高的专业素养和改编能力,把起点很高的高等数学中的抽象问题具象化,改编成高中学生认知能力范围内的题目,需要命题者在教学过程中,不断积累素材并及时进行教学研究,多尝试,多打磨,才有可能命制出一道高质量的高中数学题目.
以下几例均为函数和导数模块中,在高中常见的有高等数学背景的题目. 其中,试题5以考查函数的一阶不动点为背景,将其具象化后编制的题目,适合高一学生学完函数后作为检测;试题6和试题7实际上是以高等数学中拉格朗日中值定理为理论依据而命制的题目,学生如果知晓该定理的简单含义或是几何意义,可转化为导函数取值范围问题或通过高中“构造函数”的思想进行解答,适合高二学习导数后作为试题检测;试题8(2)可以用高中函数和导数知识及换元思想完成解答,但实际上若能化归成近年高考中高频考点“极值点偏移”问题,更易找到巧妙解法,而“极值点偏移”的背景是高等数学中连续函数凹凸性的问题,该题对学生的能力要求较高,可在高二学过导数后作为考试的压轴题目.
试题5:已知函数y=f(x)在定义域(0,+∞)上是单调函数,若对任意x∈(0,+∞),都有ff(x)
-=2,则f
的值是________.
试题6:已知函数f(x)=-x3+ax2+b,若y=f(x)图像上任意不同两点连线的斜率都不大于1,则a的取值范围是______.
试题7:已知函数f(x)=x2-2x,g(x)=logax(a>0,a≠1). 如果h(x)=f(x)+g(x)是增函数,且h′(x)存在零点(h′(x)为h(x)的导函数).
(1)求a的值;
(2)设A(x1,y1),B(x2,y2)(x1 试题8:已知函数f(x)=lnx-ax,a为常数,a∈R. (1)讨论函数f(x)在定义域上的单调性; (2)若函数f(x)有两个零点x1,x2,证明:x1x2>e2. 3. 注重整体性,用科学的标准评价试题、试卷的质量和效果 每张试卷都是一个有机整体,各类型题目要合理搭配才能保证整体性. 命题过程中除了要确保做到符合学情、科学无误、表述精准简洁、难度适宜、导向正确外,还应该注意以全国卷的标准来把控试卷的难度系数、信度、效度和区分度. 可以用高考试题常用的公式计算上述指标,并在考前预测和考后检测两个环节中,检验试卷预期考核效果和实际考核效果的符合程度,及时进行命题工作的总结和反思,使得后续的命题工作更切合实际,更贴近高考. 高考常用的各项指标的计算过程和方法很复杂,每项指标都要用多种不同的方法进行计算,高中教师无法对每次测试的结果都进行如此细致专业的分析,但可以用简化的方式实现上述重要指标的测试. 现提供公式如下,仅供参考: (1)区分度μ:分数前27%的得分称为高分组,后27%的得分称为低分组,则μ=. (2)信度α:σ表示第i道题目的方差,σ表示总得分的方差,k表示题目的个数,则信度系数公式为α= (3)难度P:①客观性试卷难度P的计算公式:P=(k为答对该题的人数,N为参加测验的总人数);②主观性试卷难度P的计算公式:P=(x为试卷平均得分,M为试卷满分);③适用于主、客观试卷的计算公式:P=(PH,PL分别为针对高分组和低分组的难度值). (4)效度:效度是指考试有效性或正确性的质量指标,即是否考了要考的内容,试题难度、区分度是否适宜,考试最终是否达到了它的预定目的. 试卷效度主要有内容效度、结构效度. 一般来说,除了要根据教学要求和有效性的理论对试卷的内容进行考察以外,还需采用计算相关系数的方法,即计算出本次试卷与另一份已被确定能正确反映受试者水平的试卷之间的相关系数来反应试卷的效度. [?] 关于高中数学试题命制的一点思考 1. 明确试卷功能对试题命制工作的影响 目前的高中数学试卷按功能区分,大致有侧重于同步检测的诊断性试卷(如单元测试),侧重于阶段性知识技能考查的评价性试卷(如期中、期末考试),侧重于群体区分的选拔性试卷(如高考),侧重于学科人才选拔的竞赛性试卷. 不同功能的试卷,在难度、目标、导向等方面均有不同的要求,同时还要因时因地制宜,符合应考学生群体的认知水平和心理承受能力. 非毕业年级主要承担前两种功能的试题命制,如诊断性试卷注重专题知识的深度和对知识技能应用的灵活度,目的就是查缺补漏、阶段检测,可适当地出现个别新颖别致的非常规考题,但在知识考查的广度上,就必须有所限制;而评价性试卷是对一个学习周期内学生学习效果的综合评定,需要涵盖该时段内的基础知识、基本技能、主要思维能力和数学思想方法,要具有一定的综合度和区分度,同时也要注意难度适中,保证试题信度和效度,以达到检测的目的. 2. 用规范的操作程序,保证试卷的整体质量 命制评价功能的数学试卷,一般要经历四个重要的程序: 首先,要編制双向细目表. 分析当下考试情况,结合学情,根据双向细目表的内容、能力层次要求和课时比例,制定整套试卷的知识点分布、题型分布、能力要求、试卷布局和结构.
其次,编制各类试题形成试卷初稿. 要注意选题原则,题目的内容能代表阶段知识的重点、难点,选题素材具有普适性(全国卷的命题往往基于教材,基于知识交汇点,基于高等数学背景). 以此为指导思想,尽力拟合高考对知识和能力的要求,重视通性通法型问题的考查,重视数学思想在题目中的渗透,重视题目背后的数学文化,但务必要适合非毕业年级学生的具体情况,切忌变成高考复习题.
再次,解答全卷预测难度. 初稿形成后,命题人要先对试卷进行全面完整的作答,记录时间,评估单题和整套试卷难度. 通常情况下,全国卷高考数学难度系数在0.6左右,竞赛考试的试卷难度在0.3至0.5左右,而单元检测、期中考试、期末考试难度不宜过大,难度系数控制在0.6至0.8左右. 事实上,难度预测本身就是很复杂的过程,主要依赖于教师的教学经验和对全国卷数学试题难度的熟悉.
最后,试题微调订立评分标准. 按照高考数学命题规范,调整初稿中表述不规范之处,力求条件简洁;知识的使用过程准确无误,改编偏、难、怪的试题形式;设计数据,让数据处理自然、流畅;预判试题或试卷对学生能力水平的鉴别能力,使能力强的学生得高分,能力差的学生得低分,即注重试题区分度的设定,如果是重要的考试,可按照高考现行的区分度计算方法进行预测评估:一般区分度在0.4以上为优秀,0.3至0.4之间为良好,0.3以下为不合格. 最后的微调还要注意应用型问题的实际背景是否符合学生的身心特点,保证背景公平. 当题目全部调整合适后,即可按照高考的分制和分值订立科学的评分标准.
3. 非毕业年级命题既要适应新高考又不可全然为了高考
非毕业年级命题策略调整的直接目的,是适应新高考制度下全国卷对数学思想方法、数学思维、数学应用和数学文化的考核方法,但本质目标是通过新评价标准的执行,检测新课程理念对数学人才培养目标的实现程度,进而更好地达成目标. 所以在非毕业年级的教学和评价环节,要立足于人的全面培养和考核,因此绝对不能在起始年级就执行只教高考考纲内容、只考高考常考考点的“应试”策略. 可在学生能力范围内,适当放宽考核范围和考查难度,注重试题灵活性、创新性和思辨性,非毕业年级有时间和精力,适当摆脱考纲的束缚,最大程度上培养学生的数学素养,即逻辑推理、数学抽象、直观想象、数学運算、数据分析能力,真正做到以考养学,以考养能,以考养才.
