超临界CO2增透煤微观图像重构及三维数值模拟*

岳立新，孙可明

(1.辽宁工程技术大学 机械学院，辽宁 阜新 123000；2. 辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

数字出版日期： 2017-01-13

0　引言

目前，我国95%以上的高瓦斯和突出矿井所开采的煤层均属于低渗透煤层，且约53%的煤炭资源处于千米以下，随着开采深度的增加，煤层的渗透性愈加降低，因此，有效提高低渗透煤层的渗透性是瓦斯抽采的一个瓶颈。目前，众多学者利用煤对CO2的吸附能力比CH4高的性质，进行CO2驱替煤层甲烷的实验研究，取得了一系列的研究成果[1-4]。CO2高于临界温度和临界压力达到超临界状态时，除了具有常规CO2的降低分压、竞争吸附作用外，还具有零表面张力、低粘度、强扩散和强溶解能力等作用。杨栋[5]从吸附解吸方面进行了超临界CO2对煤样的抽提改造实验，发现超临界CO2对煤层瓦斯的驱替效果良好。孙可明、岳立新等人[6-8]进行了不同条件下超临界 CO2的增透实验，得到了热力化学耦合作用下低渗透煤层瓦斯抽放孔注入超临界CO2渗流扩散等运移规律，实验证实了利用超临界CO2改造低渗透煤层的渗透性具有良好的增透效果。

由于组成煤体的各种矿物颗粒热膨胀和弹塑性性质的不同且又是随机分布的，引起颗粒间变形的不协调性，从而影响煤体的渗透性。目前，已有一些学者在考虑热应力等影响因素的基础上建立了各种煤体的热力耦合的本构模型，对CO2在煤体中的运移规律进行模拟研究。白冰等[9]通过引入煤岩对气体的吸附势函数，给出了考虑CO2吸附的煤岩热弹性模型的一般形式。唐书恒等[10]开展了注CO2驱替煤层甲烷的实验模拟研究,利用扩展Langmuir方程计算了驱替过程中CH4组分的产出特征。但目前还没有相关文献对超临界CO2在煤体中的运移规律进行模拟研究。因此，基于宏观超临界CO2增透煤样内部真实细微观结构，利用数字图像处理技术进行煤体非均匀结构特征的数值表征，构建三维实体模型，真实再现煤岩内部微观结构，建立超临界CO2增透煤热流力耦合力学模型，模拟不同注气条件下超临界CO2在低渗透煤层中的运移规律，这些研究将对低渗透煤层渗透性的改善提供重要的科学依据。

1　超临界CO2增透煤热流力耦合力学模型

超临界CO2在煤中运移是温度场、渗流场、应力场共同作用的动态热-流-固耦合过程，在建立超临界CO2增透模型前进行相应的假设：(1) 煤体变形符合小变形假设；(2) 超临界CO2在煤层中的渗流规律符合达西定律；(3) CO2流体和固体之间瞬间达到局部热平衡；(4)孔隙率的变化除了孔隙压力、温度和有效应力的影响外，还包括超临界CO2的抽提作用。

1.1　孔隙率和渗透率关系

前期微观实验得到了孔隙率随孔隙压力和温度的变化关系，即：随着孔隙压力的增加，孔隙率呈正指数递增的趋势：

φP=φ0emP

(1)

式中：m为大于零的拟合系数。

随着温度的增加，孔隙率呈负指数递减的关系，即：

φT=φ0e-nT

(2)

式中：n为大于零的拟合系数。

依据文献[8]，有效应力的增加会抑制煤层中孔隙、裂隙的增加，且有效应力与孔隙率之间符合负指数关系：

φe=φ0e-fσe

依据前期实验，考虑孔隙压力、温度及有效应力的影响，得出超临界CO2作用后煤样的孔隙率随孔隙压力、温度及有效应力变化的函数关系：

φ=φ0eaP-bT-cσe

(3)

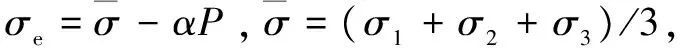
孔隙介质中渗透率与孔隙率的大小有关，根据文献[11-15]实验总结出的孔隙介质中渗透率与孔隙率之间的三次方关系：

(4)

将式(1)代入式(2)得到渗透率方程：

k=k0(eaP-bT-cσe)3

(5)

式中：k为渗透率；k0为初始渗透率，由实验得出。

1.2　煤体变形场控制方程

1.2.1弹塑性损伤本构方程

煤是多孔隙-裂隙的双重介质，在载荷作用下，其内部的孔隙、裂隙将会发生开启、扩展及汇合连通等变化，同时温度变化产生的热应力，又将引起微观缺陷的变化。煤体微观缺陷的演化在宏观层次上表现为力学性能的劣化，直至对材料单元体造成损伤，导致煤体的最终破坏。

超临界CO2作用于煤体后，图1所示，煤体出现了大量的微观缺陷，煤表面变得松散，并产生了许多“沟壑”，煤中形成长度不一的大小裂隙，微观孔裂隙的数量、形态、大小等都发生相应的变化，从而引起煤体的损伤。在SEM图像上变现为灰度的变化，因此本文基于增透后煤微观图像灰度的变化研究煤体的损伤演变过程，根据二值化图像统计出灰度值等于1的像素点的个数(即白色区域的面积), 得到以面积为基准量的损伤变量:

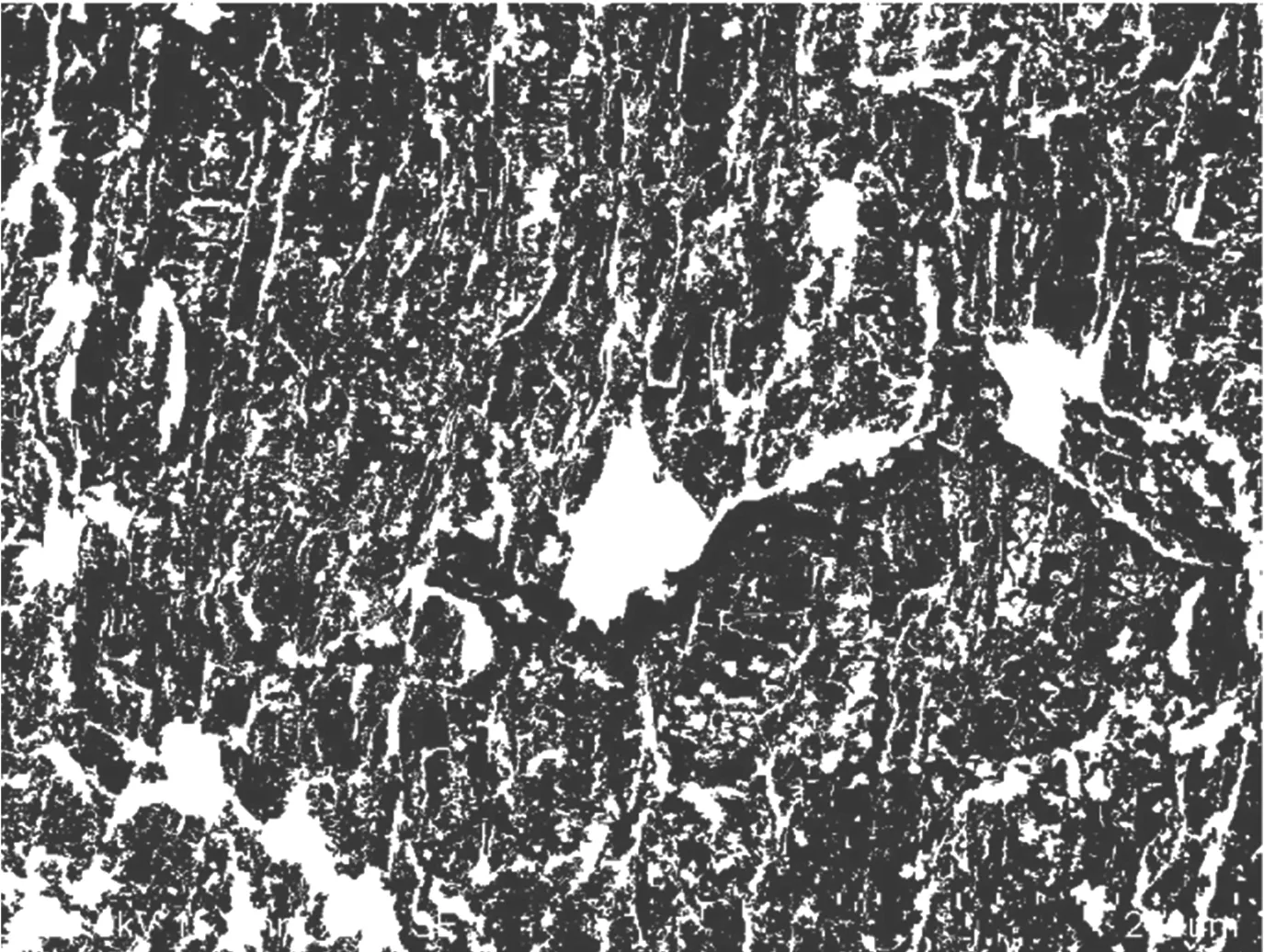
图1　超临界CO2作用后煤二值化图Fig.1　Binarization pictures of coal after the action of super critical carbon dioxide

(6)

式中：A*为煤体损伤区的面积；A为煤截面的总面积；n1为分割后的二值图像中灰度值等于1的像素点的个数；n为图像所有像素点的个数，则损伤变量可以用孔隙率的变化表示。

根据Picander提出的渗透率和损伤之间的关系方程[14]：

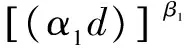
(7)

式中：d为损伤变量；α1和β1是常数，α1取值为9.4～12.3，文中取9.5；β1取值为1.6～1.8，文中取1.65；k为渗透率；k0为初始渗透率。

由式(4)的渗透率与孔隙率之间的三次方关系，联立公式(7)，得到损伤变量与孔隙率之间的关系方程：

(8)

即：

(9)

式中：φ=φ0eaP-bT-cσe。

则考虑孔隙压力和热应力的增量形式的弹塑性本构关系为：

(10)

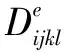
1.2.2几何方程

根据小变形假设，几何方程为：

(11)

1.2.3平衡方程

(12)

式中：σij为应力张量的分量；bi为体积分力。

则由式(6)-(8)，平衡微分方程为：

(13)

在描述煤岩材料的塑性行为时，选用 Drucker-Prager 屈服准则，则塑性屈服函数方程为：

(14)

式中：α和κ为材料参数。

1.3　渗流场方程

基于质量守恒定律，超临界CO2在煤层中的质量守恒方程为：

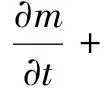
(15)

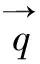
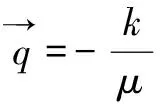
(16)

式中：k为渗透率；μ为超临界CO2的黏度。

煤层中超临界CO2含量为吸附CO2量和游离CO2量之和，即：

(17)

式中：φ表示孔隙率;ρc表示煤体介质的密度，kg/m3;ρ为CO2的密度，kg/m3，ρ=βp，β为压缩系数；VL和pL分别为Langmuir体积常数和压力常数。

则有：

(18)

把式(18)和式(16)代入式(15)得：

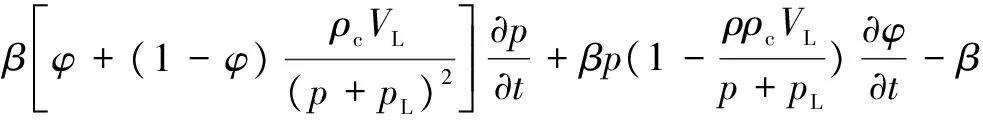
(19)

其中孔隙率的变化为：

(20)

将式(20)代入式(19)中得渗流场方程为：

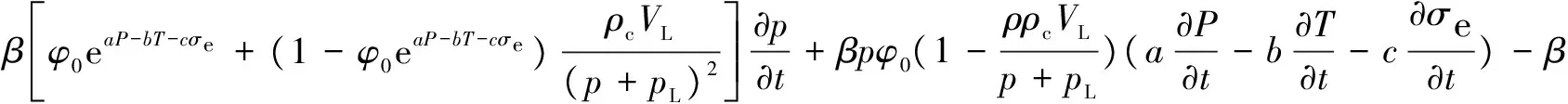
(21)

1.4　温度场控制方程

由传热学知，温度场控制方程为：

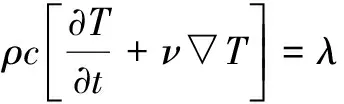
(22)

式中：ρ为密度；c为比热；λ为热传导系数；Q0为热源汇项。

1.5　定解条件

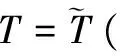
2　数值模拟

2.1　计算模型重构

组成煤岩的各种矿物颗粒热膨胀和弹塑性性质的不同及其分布的随机性，使得煤岩颗粒间的变形不协调，影响流体在煤岩微观孔隙中的流动。本文借助于增透后煤样微观图像，并采用体绘制的方法[15]，将图像处理技术与有限单元法相结合，建立能够反映煤体内部真实细观结构的有限元数值计算模型，构建出三维实体模型如图2所示。

图2　三维数值模型Fig.2　3 d numerical model

将不同的单元分别赋予不同的材料属性，以真实再现煤层内部的孔裂隙系统。相关计算参数如表1所示。

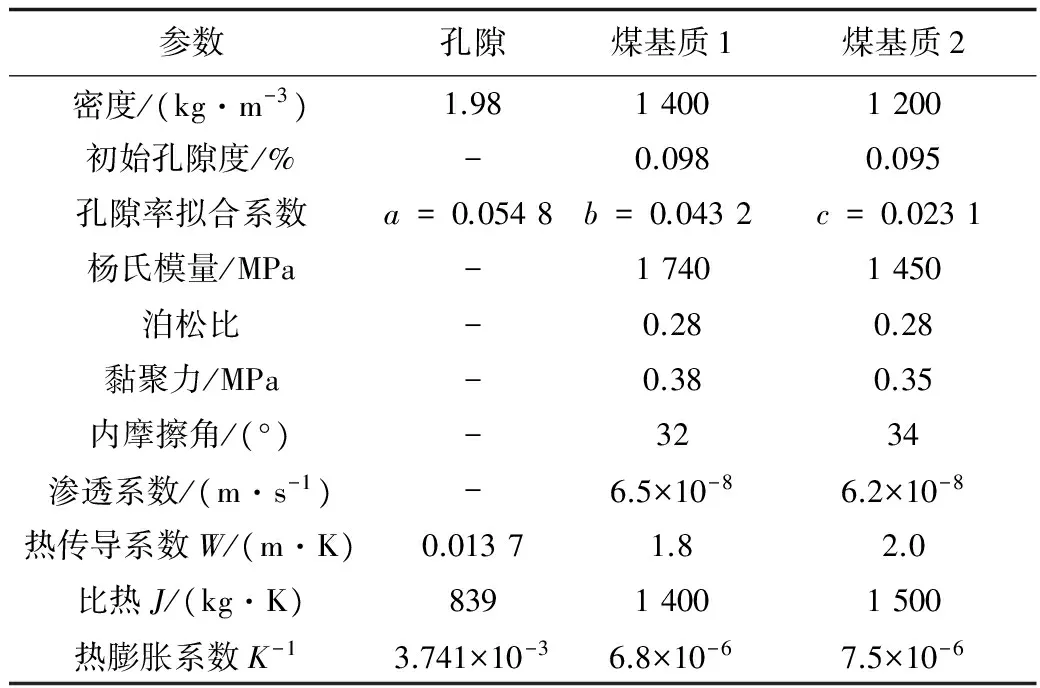
表1　计算参数

假设模型处于静水压力作用下，给定围压σy=11 MPa，轴压σx=2.88 MPa，底面和右面给定位移边界为零。模型左边界给定注气压力P=8 MPa，初始瓦斯压力为2.0 MPa，在其它边界上均设置为不产生流量交换的Neumann边界。考虑模型与外界存在热对流效应，设定模型左侧边界注气温度70 ℃，初始温度20 ℃。

2.2　数值模拟结果及分析

2.2.1有效应力变化

图3给出了不同注入超临界CO2时间，煤体有效应力的分布云图，从图中可以看出，随着煤层注入CO2时间的延长，煤体内的CO2增多，煤层注气端周围煤体骨架有效体积应力的动态变化呈现出不均匀性，这主要是由于煤体各处的弹性模量、泊松比及抗拉强度等性能参数不同所致，说明煤体内CO2流体的流引起煤体有效应力的变化，进而引起煤体骨架变形，从而又影响到煤体内流体的渗透，可见应力场和渗流场是互为影响，互为制约的。

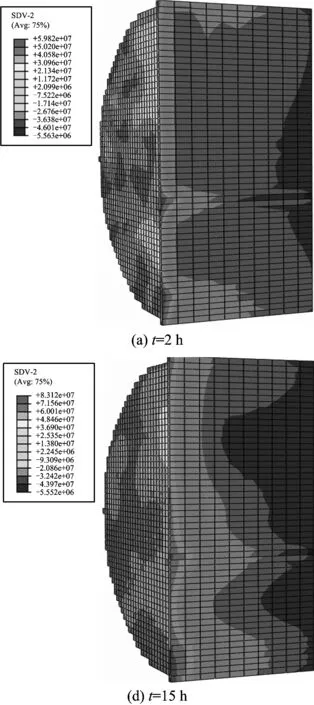
图3　有效应力随时间的变化Fig.3　The change cloud image of effective stress with time

图4　孔隙压力随时间的变化Fig.4　The change cloud image of pore pressure with time

2.2.2孔隙压力变化

图4为超临界CO2注入到低渗透煤层中，孔隙压力随时间的变化云图。可以看出，由于渗流场和应力场的液-固耦合作用, 随着煤体注入超临界CO2时间的延长，孔隙压力呈现波浪形向出气端周围呈非线性的传递蔓延，注气初期孔隙压力变化较快, 煤层注气端周围的孔隙压力不断增大，注气到一定时间后, 孔隙压力增幅变缓, 注入CO2对煤层内孔隙压力的影响范围越来越广，当注气时间达到10 h时，CO2的渗流量增多，其孔隙压力升高，孔隙压力传递波的波峰几乎波及到了出气端，表现出明显的非均匀性和随机性。

2.2.3温度场变化

随着时间的推移，温度传播过程如图5所示，CO2在一定的压力下注入到低渗透煤层中，拥有一定的流速，同时温度较高，因此CO2将与周围的煤体发生热对流，使煤体的温度逐渐升高，并向周围的煤体逐渐扩展。随时间的增加，温度传播的范围逐渐扩大。由于煤的非均质性使得煤体各处的热传导性表现出各向异性，因此温度从高温区域向低温区域的传递也是不均匀的，从图中可见温度的传递出现明显的波峰和波谷。

图5　温度随时间的变化Fig.5　The change cloud image of temperature with time

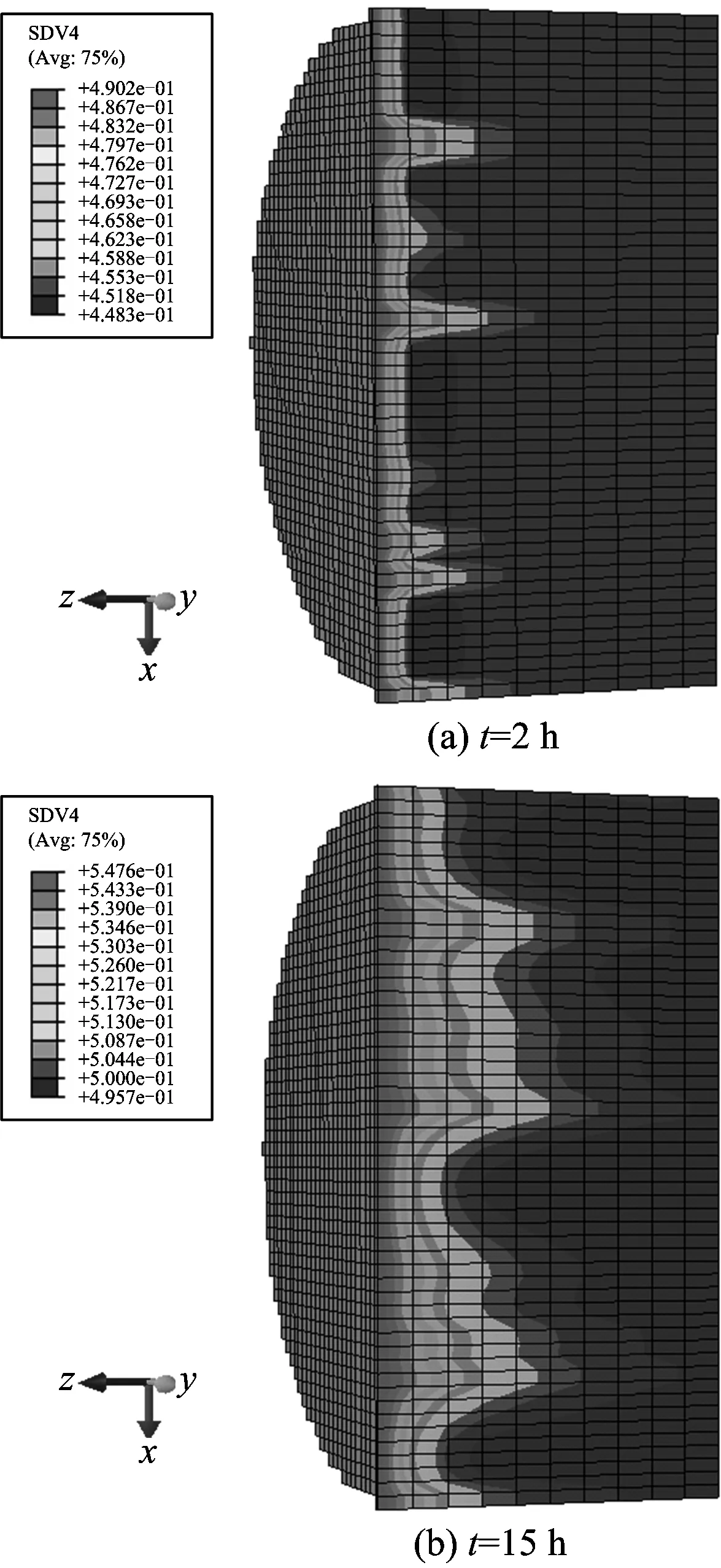
图6　损伤量随时间的变化Fig.6　The damage change with the time

2.2.4损伤变化

图6为注入超临界CO2注入过程中损伤分布云图，从图中可以看出，随着煤层注入超临界CO2时间的增加，煤体注气端向出气端，煤体损伤量不断增加，且损伤在煤体中的传递趋势快慢不一，即随时间持续，损伤向出气端周围蔓延的趋势呈现出明显的非均匀性。这是由于煤是一种非均质的多孔介质材料，内部含有大量的原始微裂隙、微孔隙等缺陷，并成随机分布状态，在一定压力和温度的超临界二氧化碳注入过程，煤体内部各处孔隙、裂隙的变形、开裂以及扩展等存在不均一性，因此，煤体各处的损伤量也不一样。

对比不同注气时间发现，随注入时间的增加，损伤波及的范围也随之增加，从而影响煤体的渗透性。

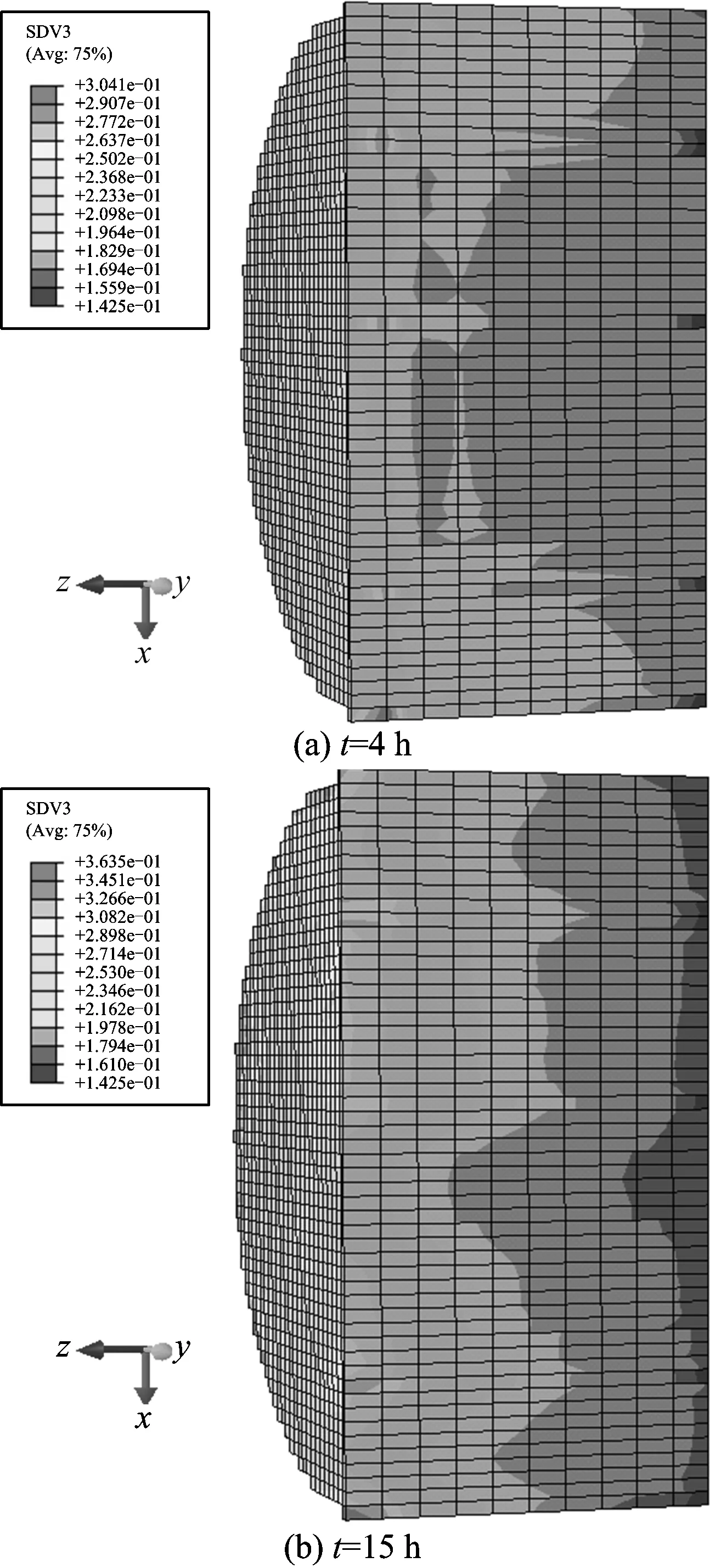
图7　孔隙率随时间的变化Fig.7　　The change cloud image of porosity with time

2.2.5孔隙率变化

图7给出了孔隙率随时间的变化云图，随着往煤样内注入CO2时间的延长，煤层内部孔隙率随时间的变化表现出明显的非均匀性和随机性，这是由于煤体各处的孔隙、裂隙是随机分布的，使得孔隙率的分布具有明显的随机性。由孔隙率的传播趋势看，随着注气时间的延长，由注气端到出气端孔隙率增加的趋势逐渐降低，注气端的孔隙率增加明显，这是由于注气端超临界CO2流量较高，对煤体的增透作用较强使得煤体孔隙、裂隙得到进一步的扩展、贯通，孔隙率明显增加，有效提高了煤微观孔裂隙结构的渗透能力，出气端孔隙压力梯度下降，超临界CO2对煤体的作用减弱，孔隙率趋于恒定。

2.2.6渗透系数变化

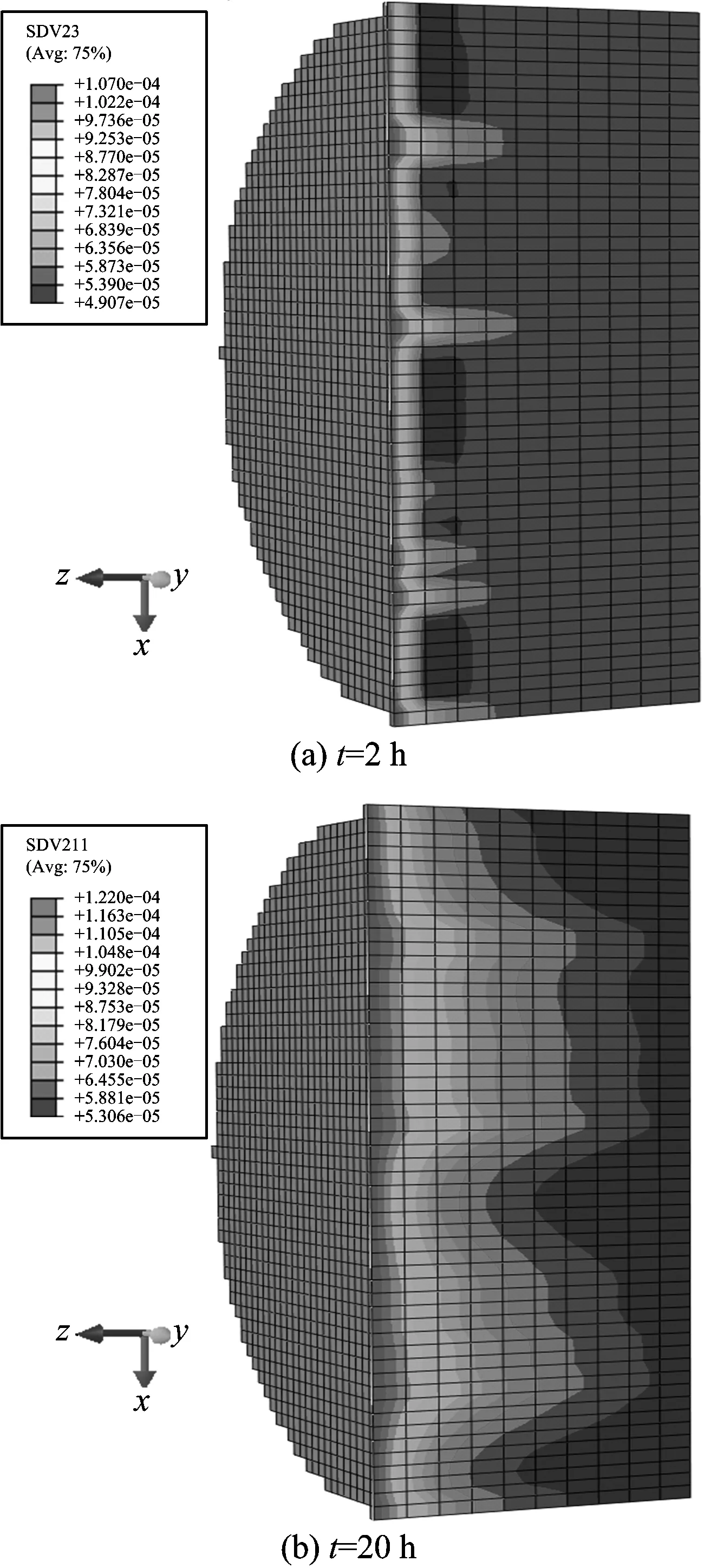
图8　渗透系数随时间的变化Fig.8　The change cloud image of permeability coefficient with time

煤体无量纲渗透系数随注气时间的变化规律，如图8所示，从图中可见，在一定压力和温度超临界CO2注入过程中，煤体的渗透系数随注气时间的增加具有统一的变化规律：渗透系数随注气时间的增大而增大，初始阶段渗透系数变化较大，这是由于注气端的孔隙压力大，超临界CO2流量多，煤体损伤程度较大，微观孔隙、裂隙发育程度增加明显，孔隙流体的渗流通道增多，因此，煤体的渗透系数增加明显。经过一定注气时间之后，煤体渗透系数增减缓慢，直至趋于稳定，这是由于随着沿程孔隙压力的降低，超临界CO2流量减少，煤体损伤增加趋势逐渐减缓，渗透系数增加的趋势变小，逐渐趋近于稳定。渗透系数的变化规律与煤体损伤及孔隙率的变化规律是一致的，说明由于超临界CO2对煤体的作用，引起煤体损伤，促进了煤体微观孔隙结构的变化，提高煤体的渗透系数。可见，在恒定孔隙压力和温度条件下，煤体注入超临界CO2时间越长，注气影响范围越大。因此，为了提高增透效果，需要保证一定的注入CO2时间。

3　结论

1)将图像处理技术与有限单元法相结合，对增透后煤样微观图像进行处理，采用体绘制的方法，开发三维重构程序，建立了能够反映煤体内部真实细观结构的三维实体模型。

2)依据增透后煤微观图像，利用孔隙率随孔隙压力、温度及有效应力变化的函数关系式，导出煤的损伤演化方程，建立了超临界CO2增透煤热流力耦合力学模型。

3)利用建立的实体模型进行应力场、渗流场和温度场的数值分析，结果表明，由于组成煤岩的各处煤基质和矿物的密度、弹性模量和热膨胀系数等物理参数的不同及其分布的随机性，导致超临界CO2注入过程中应力场、温度场、渗流场的非均匀性。

4)随着超临界CO2注入时间的延长，由注气端至出气端，由于超临界CO2的增透作用，损伤向出气端周围蔓延的趋势呈现出明显的非均匀性，煤体孔隙、裂隙得到进一步扩展、贯通，孔隙率和渗透系数增加。在其他注入参数一定的条件下，增加CO2的注入时间，有利于提高煤体渗透性。

[1]杨宏民，许东亮，陈立伟. 注CO2置换/驱替煤中甲烷定量化研究[J].中国安全生产科学技术，2016，12(5)：38-42.

YANG Hongmin，XU Dongliang，CHEN Liwei. Quantitative study on displacement-replacement of methane in coal through CO2injection[J].Journal of Safety Science and Technology，2016，12(5)：38-42

[2]梁卫国, 吴迪, 赵阳升. CO2驱替煤层CH4试验研究[J].岩石力学与工程学报,2010, 29(4): 665-673.

LIANG Weiguo, WU Di, ZHAO Yangsheng. Experimental study of coalbeds methane by carbon dioxide[J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(4): 665-673.

[3]徐春光，王延斌，王向浩，等. 深部煤层CO2置换CH4过程中煤岩特性变化研究[J].河南理工大学学报(自然科学版), 2013, 32(3):265-269.

XU Chunguang, WANG Yanbin, WANG Xianghao, et al. Research progress of coal rock properties change in the progress of CO2replacement CH4in deep coal seam[J]. Journal of Henan Polytechnic University (Natural Science), 2013, 32(3):265-269

[4]王晋，王延斌，王向浩，等. CO2置换CH4试验中煤体应变及渗透率的变化[J].煤炭学报, 2015, 40(S2):386-391

WANG Jin, WANG Yanbin, WANG Xianghao, et al. Variation characteristics of coal strain and permeability on coal-bed methanedisplacement by carbon dioxide injection[J]. Journal of China Coal Society, 2015, 40(S2):386-391

[5]杨涛，杨栋，康志勤，等.注入超临界 CO2对提高煤层渗透性的影响[J].煤炭科学技术,2010，38(4)：108-110.

YANG Tao, YANG Dong, KANG Zhiqin, et al. Influence on improving permeable performance in coal seam through injection supercritical CO2[J].Coal Science and Technology，2010，38(4)：108-110.

[6]孙可明,任硕,张树翠,等.超临界CO2在低渗透煤层中渗流规律的实验研究[J].实验力学, 2013, 28(1): 117-120.

SUN Keming, REN Shuo, ZHANG Shucui, et al . Experimental study of supercritical carbon dioxide seepage flow in low permeability coal seam[J]. Journal of Experimental Mechanics, 2013, 28(1): 117-120.

[7]岳立新,詹广强,孙可明,等. 超临界CO2提高煤层渗透性的实验[J].辽宁工程技术大学学报, 2014, 7(1):907-911.

YUE Lixin，ZHAN Guangqiang，SUN Keming，et al . Experiment study on the increasement of coal seam permeability by supercritical CO2[J]. Journal of Liao ning Technical University, 2013, 28(1): 117-120.

[8]岳立新，孙可明，郝志勇. 超临界CO2提高煤层渗透性的增透规律研究[J].中国矿业大学学报, 2014, 42(2): 319-323.

YUE Lixin，SUN Keming，HAO Zhiyong. Study on increased permeability law of coal seam by supercritical CO2[J]. Journal of China University of Mining & Technology, 2014, 42(2): 319-323

[9]白冰，李小春，刘延锋, 等.CO2吸附对煤岩热弹性模型影响的理论解释[J].岩土力学, 2006, 27(11): 1974-1976.

BAI Bing, LI Xiaochun, LIU Yanfeng, et al. A theoretical explanation for influence of CO2adsorption on thermoelastic model of coal-rock [J]. Rock and Soil Mechanics, 2006, 27(11): 1974-1976.

[10]唐书恒,马彩霞,叶建平,等. 注CO2提高煤层甲烷采收率的实验模拟[J].中国矿业大学学报,2006,35(5): 607-611.

TANG Shuheng, MA Caixia, YE Jianping， et al . A modeling experiment of enhancing coalbed methane recovery by carbon dioxide injection [J]. Journal of China University of Mining & Technology, 2013, 28(1): 117-120.

[11]杨新乐，任常在，张永利，等.低渗透煤层气注热开采热-流-固耦合数学模型及数值模拟[J]煤炭学报,2013，38(6):1044-1049.

YANG Xinle，REN Changzai, ZHANG Yongli, et al . Numerical simulation of the coupled thermal-fluid-solid mathematical models during extracting methane in low-permeability coal bed by heat injection[J]. Journal of China Coal Society,2013，38(6):1044-1049.

[12]李培超，孔祥言，卢德唐. 饱和多孔介质流固耦合渗流的数学模型[J].水动力学研究与进展，2003，18(4)：419-426.

LI Peichao, KONG Xiangyan, LU Detang. Mathematical modeling of flow in saturated porous media on account of fluid-structure coupling effect[J]. Journal of Hydrodynamics，2003，18(4)：419-426.

[13]张丽萍.低渗透煤层气开采的热-流-固耦合作用机理及应用研究[D].北京：中国矿业大学，2011.

[14]翁其能, 吴秉其, 秦伟. 地下结构混凝土渗透损伤研究综述[J].材料导报，2014, 28(16):130-133.

WENG Qineng, WU Bingqi, QIN Wei . The process of the damage in concrete penetration study [J]. Materials Review，2014, 28(16):130-133..

[15]万成.基于X-rayCT和有限元方法的沥青混合料三维重构与数值试验研究[D].广州：华南理工大学，2010.