带偏置点的绳系拖拽离轨系统动力学研究*

刘贺龙，何英姿，谈树萍

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100194)

带偏置点的绳系拖拽离轨系统动力学研究*

刘贺龙1，2，何英姿1，2，谈树萍1，2

(1.北京控制工程研究所，北京100190;2.空间智能控制技术重点实验室，北京100194)

考虑空间拖船利用飞网/飞爪对空间残骸捕获结束后绳系拖拽系统的动力学特性，开展了基于简化的带偏置点构型的建模及仿真研究.首先，捕获后的组合体包括空间拖船、系绳和空间残骸，系绳在空间残骸一端的牵挂点看作偏置点，给出相应的的绳系拖拽系统构型;其次，以降轨离轨过程为例，建立系统能量方程，并根据欧拉-拉格朗日方程给出系统的动力学表达式并估算系绳张紧情况下的平衡点;最后，设定离轨推力，在不同的初始角速度、系绳张紧或松弛以及不同松弛程度条件下，分析绳系拖拽离轨系统的动力学行为.研究表明，空间残骸小的初始角速度和张紧或略微松弛的系绳能够保证安全离轨.

绳系拖拽;偏置点;安全离轨;

0 引言

人类进行太空探索活动已将近60年，导致地球轨道上废弃卫星和残骸的急剧增加空间环境恶化.由于轨道上物体高速运动，某些轨道上发生碰撞的危险太高使其不再适于卫星运行，两个星体的相撞将会导致数以千计的小的高速碎片，空间环境将进一步恶化［1-2］.以GEO轨道为例，GEO轨道资源是极其宝贵且有限的［3］，理论上最多能容纳1 800颗卫星［4］，但随着在轨运行卫星和废弃卫星的增多，该轨道也势必变得更加拥挤，研究轨道清理的离轨技术具有重大的理论和实际意义.目前，研究人员已经提出了几种技术来实现对废弃卫星或残骸的移除.

绳系技术是目前离轨技术中的一个分支，以往的研究多侧重于绳系卫星技术，包括子卫星的释放、回收和在轨保持等.绳系离轨技术的关键点在于利用不同的绳末端部件，如飞网［5］、在绳端的空间机器人［6］或单独附着于空间残骸上的系绳［3，7］等，满足不同的任务和需求.例如，绳系拖拽的离轨技术可以清理轨道上的废弃卫星和部件;绳系卫星变轨技术可以节约通讯卫星的燃料;完成空间补给任务等.

目前，关于绳系卫星在轨保持、释放和回收的研究较多，关于绳系拖拽变轨/离轨的研究较少.Cho和McClamroch［8］提出了一种最优变轨技术，作用于空间拖船上的连续推力用来实现在两个圆轨道间的轨道转移.针对小的连续常值推力的化学推进绳系卫星系统，Sun等［9］基于欧拉-拉格朗日方法，采用哑铃构型建立了绳系拖拽系统的模型，将推进作用归一化为绳系卫星系统的推进系数，详尽分析推进系数对绳系卫星系统平衡点的影响，并利用分层滑模的设计方法设计了系绳张力控制律，实现了变轨过程中对面内摆角的抑制.Liu等［10］研究了GEO轨道上绳系拖拽离轨问题，将空间残骸和空间拖船看作质点，考虑系绳断裂、空间拖船与空间残骸碰撞和系绳缠绕等风险，着重研究了包含加速、平衡、旋转和返回的四阶段变轨策略.考虑空间残骸转动惯量、系绳长度和初始角速度的影响，Aslanov［11］研究了通过系绳连接的空间残骸与空间拖船组合体的动力学问题，研究表明，若空间拖船推力的方向与系绳方向一致，且系绳保持张紧，那么离轨过程就是安全的.一般来说大气阻力的影响在轨道高度300 km以上可以忽略不计，若空间残骸相比空间拖船有较大的横截面积，那么在空间拖船拖拽残骸再入过程中，由于气动力作用空间残骸将快速减速，两者间可能会发生碰撞，在文献［12］中，Aslanov设计了一种推力控制策略以避免碰撞.针对空间拖船和废弃星的绳系组合体，考虑废弃星上的弹性部件，如帆板的影响，文献［13］研究了系绳振动和帆板弹性模型的相互作用，给出了上述描述问题的数学模型，对其简化模型的分析给出了针对特定废弃星参数的系绳刚度特性的要求.

本文结合一个仿真算例，在水平拖拽过程中，对绳系拖拽系统进行建模和动力学分析，深入分析不同的任务星初始状态及系绳的初始状态对系统动力学演化的影响，分析目标星相对系绳的姿态角，从定性的角度给出较文献［11］更为宽泛的能够保证拖拽任务安全的工作条件，并给出一些建设性的建议.文章安排如下:首先以绳网为例，对捕获后的拖拽离轨系统进行问题描述，其次，以轨道系为参考坐标系建立系统的动力学方程;然后分析不同的初始条件下空间残骸相对系绳的摆角变化及系绳绳长的变化，给出能够保证拖拽离轨过程安全的一些条件，给出捕获系统的一些设计参考和建议.

1 空间拖拽问题描述

以ROGER项目［14］中飞网捕获为例，空间残骸被捕获后构型如图1所示.

图1 飞网捕获空间残骸Fig.1 Space debris captured by a net

收口完成后，飞网将包裹住空间残骸，将飞网与空间残骸看作一个整体，此时系绳与空间残骸的连接点将等效成一个牵挂点，显然，该点不在空间残骸质心，称之为偏置点.一般来说，该偏置点到空间残骸质心的距离在几米的数量级，而空间拖船和空间残骸间的系绳长度为几十米的数量级，相较于传统绳系卫星研究中两星之间千米数量级的距离，在本研究中需要考虑偏置点对拖拽过程的影响.绳网拖拽离轨过程可理解为升轨离轨和降轨离轨操作，以降轨离轨过程为例进行研究，不考虑绳网拖拽系统的轨道运动，仅研究在拖拽过程中，空间残骸相对系绳的姿态运动及空间拖船与空间残骸间的相对距离.

2 拖拽系统动力学模型

2.1 坐标系定义

空间拖船-系绳-空间残骸的构型如图2所示，图3表示的是空间残骸本体坐标系到系绳坐标系的姿态旋转.

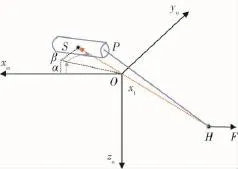
图2 绳系拖拽系统示意图Fig.2 Configuration of tether tugging deorbiting system

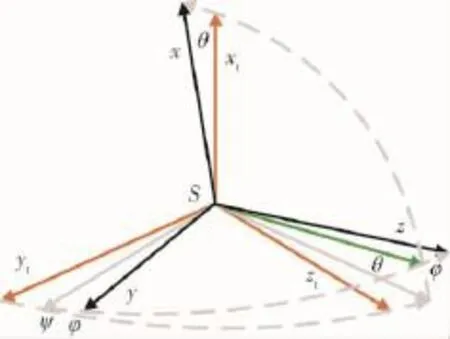
图3 姿态角定义Fig.3 Definition of Attitude

本研究中，H为空间拖船质心，S为空间残骸质心，O为二者质心.参考坐标系Oxoyozo以O为原点，Oyo沿轨道面负法向，Ozo指向地心，Oxo沿组合体前进方向，广义坐标定义为q1，2=x，y;绳系坐标系Sxtytzt原点位于空间残骸质心，该坐标系由Oxoyozo作旋转α(2)→β(3)得来，括号内代表旋转轴顺序，α，β分别描述绳系系统的面内和面外摆角，空间拖船与空间残骸质心的距离SH=s.定义广义坐标q3=s，q4=α，q5=β，如图2所示;空间残骸本体坐标系Sxyz按转序ψ(1)→θ(2)→φ(1)得来，括号内代表旋转轴顺序，定义广义坐标q6=ψ，q7=θ，q8=φ，详见图3.Oxoyozo到Sxtytzt的旋转矩阵Cto= C3(β)C2(α);Sxtytzt到 Sxyz的旋转矩阵 CBt= C1(φ)C2(θ)C1(ψ).空间残骸本体相对Sxtytzt的角速度为

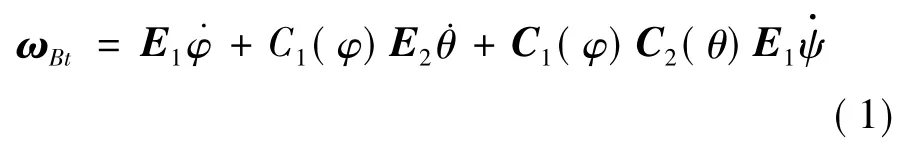
Sxtytzt相对Oxoyozo的角速度为

其中，E1=［1 0 0］Τ，E2=［0 1 0］Τ，E3=［0 0 1］Τ，那么，空间残骸相对参考系Oxoyozo的角速度为:

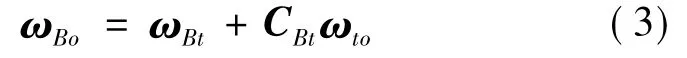
系统质心在参考系 Oxoyozo内的坐标表示为ρO=［x，y，0］Τ;

空间拖船质心在参考系Oxoyozo内的坐标表示为，速度表示为

空间残骸质心在参考系Oxoyozo内的坐标表示为，速度表示为

其中，ηS=mS/(mS+mH)，ηH=mH/(mS+mH)，mS为空间残骸质量，mH为空间拖船质量，定义空间残骸的转动惯量J=diag{Ix，Iy，Iz};定义绳网系统在空间残骸上的附着点P为rPB=［a，b，c］Τ，在坐标系 Oxoyozo内，该点的坐标描述为:rPO=rSO+系绳在 Oxoyozo内表示为 l=rHP=rPO- rHO，系绳单位向量表示为

系绳绷紧时，作用于系绳上的张力大小表示为

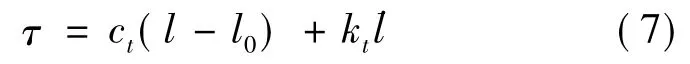
其中，ct为弹性系数，kt为阻尼系数，l0为绳系初始长度，rHO为l的绳长.

2.2 动力学方程

根据上节各表达式，组合体系统的总动能:

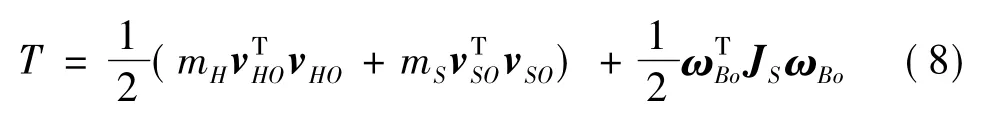
本例中，系绳单位向量的方向始终与空间残骸所施加力的方向相反.在参考系Oxoyozo中，由系绳产生的作用于空间拖船的力表示为FH=τul，系绳产生的作用于空间残骸的力表示为FS=-FH=-τul;由变轨推力产生的作用于空间拖船的力F=［Fx，Fy，0］Τ.由此，可计算出各广义坐标对应的广义力为

由欧拉-拉格朗日方程

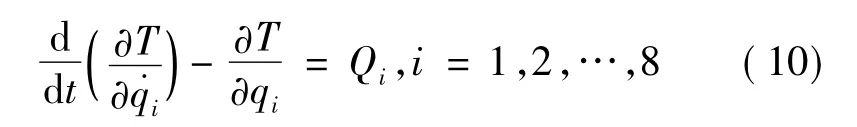
即可得到绳网系统捕获后，拖拽离轨过程中系统的动力学方程.

本文重点考虑拖拽离轨过程中空间残骸相对系绳的姿态运动，讨论不同初始工况下，系绳与空间残骸是否会发生缠绕.由式(8)～(10)可以看出，给出系统的动力学表达式将带来非常繁重的数学推导工作，虽能给出一般的表达结论，但非常不利于研究分析.因此进行简化处理，假设空间残骸是绕x轴的轴对称体，即Ix≠Iy=Iz，网收紧后，偏置点在负x轴端，即b=c=0，初始时刻，系统处于水平拖拽状态，无面外拖拽力，Fx=F，Fy=0，此时系统动能表示为

广义力表达式分别表示为Qx=F，Qy=0，Qα=0，Qβ=0，Qs=-ηSF+(s+acosθ)τ/l，Qφ=0，Qψ=0，Qθ=(saτsinθ)/l，此时绳长的表 达 式 l=降轨离轨过程中，绳网系统在空间残骸上的附着点a＜0，此时θ的平衡点为0，面内摆角α的平衡点也是0;若是升轨过程，绳网系统在空间残骸上的附着点为a＞0，此时θ的平衡点为-π，面内摆角的平衡点也是-π.

由以上广义力的表达式可以看出，仅需考虑广义坐标s和θ的运动.这里可以理解为:在简化的拖拽模型中，我们仅关心任务星与空间残骸的质心距离和空间残骸的俯仰角运动.研究质心间距的目的是探讨拖拽过程中，任务星与空间残骸是否会发生碰撞;根据空间残骸姿态角的定义，研究其俯仰角的目的是探讨空间残骸是否会与系绳发生缠绕和切割行为，并进一步分析拖拽过程是否安全.由欧拉-拉格朗日方程，给出如下形式的首次积分:

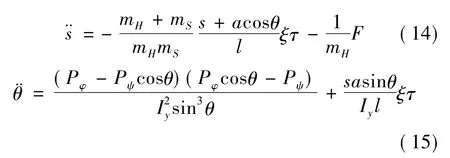
当θ=0时，拖拽系统的动力学方程表示为:

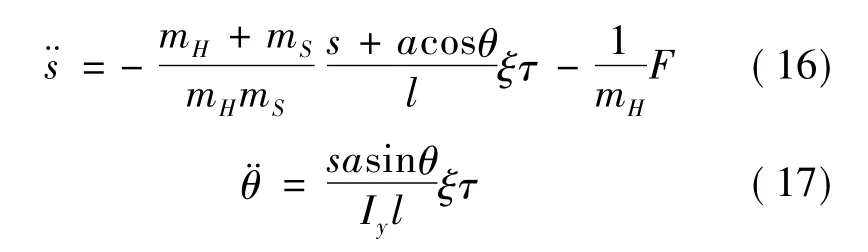
其中，ξ的表达式为:

以系绳张紧为例，在一般情况下，对式(14)～(15)的平衡点进行分析.理想平衡状态下，系绳长度看作定值，假设 ˙φ=0，l≈s+acosθ，令可得或 sinθeq=0.令Γ=cosθeq，系统平衡点为

3 仿真分析

考虑系绳的弹性效应和阻尼效应，给定参数为: Ix=3 000 kg·m2，Iy=Iz=10 000 kg·m2，a=-2 m，b=c=0，mH=1 000 kg，mS=3 000 kg，弹性系数为ct=589 N/m，阻尼系数kt=104 N·s·m-1， F=-20 N.给定初始条件，空间拖船质心到牵挂点初始距离l*0=50 m，若系绳张紧，那么在拖拽过程中，该距离表示为l，初始绳长l0=50 m，定义绳长偏差仿真结果如图4所示.

图4 初值为零条件下绳长偏差Fig.4 Tether length variation in zero initial condition

该仿真结果表明拖拽过程中，在初值为零条件下，弹性效应导致系绳变长，阻尼效应使得该形变的振幅随时间越来越小，最终系绳阻尼效应引起的系绳张力为零，系绳形变引起的张力大小为15 N，与|F|ηS的值一致;由拖拽系统动力学方程易知，空间残骸的俯仰角相对系绳坐标系将始终为0，表明在零初值条件下，拖拽降轨离轨过程是一个安全的过程.

下面讨论不同非零初始条件下系统的动力学行为.不同的初始条件意味着空间拖船不同的初始角速度、系绳张紧/松弛和不同松弛程度等.

Case A:系绳张紧，不同初始角速度

在系绳张紧的前提下，考虑到空间残骸相对系绳坐标系角速度的表达形式(1)，令，选取不同的值(仿真图中示作ψ')，分别选取为= 0.05 rad/s，=0.071 6 rad/s，=0.09 rad/s，= 0.12 rad/s.此时，系统平衡点依次为θeq=0，θeq= 0.525 9 rad，θeq=0.999 7 rad，θeq=1.264 8 rad.仿真结果以线型对上述4种情况进行区分，依次对应实线、点划线、虚线和点线.仿真结果如图5～7所示.

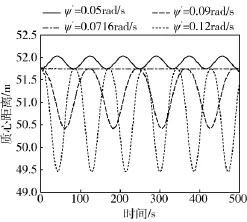
图5 质心距离曲线—Case AFig.5 position of mass of center in Case A

图6 绳长偏差曲线—Case AFig.6 Tether length variation in case A

图7 俯仰角曲线—Case AFig.7 Pitch angle curve in Case A

Case B.系绳固定松弛长度，不同初始角速度

在系绳松弛的条件下，采用与A中一样的初始条，绳长偏差初值=-2 m，仿真结果如图8～10所示:

从图8～10仿真结果可以看出，在系绳松弛条件下拖拽过程将表现的更加复杂，根本原因在于空间残骸一直在自由漂浮与受迫运动间切换，但仍有一定的规律:从图8～9可以看出，由于初始时刻系绳松弛，拖拽过程中，系绳松弛的长度在逐渐缩短;图10表明，随着初始时刻角速度的增大，拖拽过程中俯仰角的幅值也在增大，小的角速度初值对拖拽过程影响不大，若角速度初值达到一定范围后，也会发生系绳与空间残骸缠绕的危险，不利于拖拽过程.

图8 质心距离曲线—Case BFig.8 Position of mass of center in Case B

图9 绳长偏差曲线—Case BFig.9 Tether length variation in Case B

图10 俯仰角曲线—Case BFig.10 Pitch angle curve in Case B

Case C.固定初始角速度，不同松弛长度

图11 绳长偏差曲线—Case CFig.11 Tether length variation in Case C

图12 俯仰角曲线—Case CFig.12 Pitch angle curve in Case C

Case C的仿真结果表明，在给定的初始条件下，当系绳松弛长度逐渐增加时，在拖拽离轨过程中，绳长偏差仍可逐渐变小，俯仰角仍在一定范围内波动，但随着初始松弛长度的增加，摆角幅值急剧增大，篇外的试验表明，若再增加初始松弛长度，系绳将与空间残骸发生缠绕，拖拽过程不再稳定.

4 结论

本文开展了绳系拖拽系统的动力学建模问题及仿真研究，这一类问题由飞网/飞爪捕获系统简化而来.捕获后的组合体包括空间拖船、空间残骸和系绳，在偏置点存在的条件下，分别给出各坐标系的定义，给出组合体系统的动能方程;针对一种简化的拖拽情况，通过欧拉-拉格朗日方法建立了这种工况下姿态角和两星质心距离的运动方程;在空间拖船不同的初始角速度、初始系绳张紧/松弛和不同初始松弛程度条件下，研究了绳系拖拽系统的动力学行为.研究表明，在系绳张紧或较小的松弛程度前提下，小的初始角速度能够保证拖拽离轨过程是安全的.

根据简化模型分析绳网拖拽离轨过程的研究结论，给出如下几点建议:

首先，对空间残骸采用绳或绳-网组捕获前，应大致确定空间残骸角速度信息，以确认该目标能否直接捕获，否则反向提出对空间拖船的任务需求;

其次，确认空间残骸的自旋轴，沿轴捕获，并配合合适的部件，如万向结，将极大程度上克服空间残骸自旋导致的系绳扭转问题，保证任务成功;

最后，确保绳或绳网释放并捕获后，系绳处于绷紧或略有松弛状态，保证空间拖船与系绳在拖拽过程中不发生接触或缠绕，例如在空间拖船一端增加卷扬机构用以控制绳长，同时也可以增加张力检测装置，通过控制系绳上的张力来稳定空间残骸与系绳的相对姿态;考虑用网对空间残骸进行捕获的情况，收口装置应将空间残骸包裹的越紧越好，这样将极大程度上避免系绳松弛.

［1］BRADLEY A M，WEIN L M.Space debris:Assessing risk and responsilibity［J］.Advances in Space Research，2009，43:1372-1390.

［2］CASTRONUOVO M M.Active space debris removal—A preliminary mission analysis and design［J］.Acta Astronautica，2011，69:848-859.

［3］CHOBOTOV V，MELAMED N，AILOR W H，et al.Ground assisted rendezvous with geosynchronous satellites for the disposal of space debris by means of earth-oriented tethers［J］.Acta Astronautica，2009，64:946-951.

［4］李恒年，高益军，余培军，等.地球静止轨道共位控制策略研究［J］.宇航学报，2009，30(3):967-973.LI H N，GAO Y J，YU P J，et al.The strategies and algorithms study for multi-geo satellites collocation［J］.Journal of Astronautics，2009，30(3):967-973.

［5］LIU H T，ZHANG Q B，YANG L P，et al.Dynamics of tether-tugging reorbiting with net capture［J］.Science China Technological Sciences，2014，57(12):2407-2417.

［6］HUANG P F，WANG D K，Meng Z J，et al.Post-capture attitude control for a tethered space robot-target combination system［J］.Robotica，2014:1-22.

［7］ASLANOV V S，YUDINTSEV V.Dynamics of large space debris removal using tethered space tug［J］.Acta Astronautica，2013，91:149-156.

［8］CHO S，MCCLAMROCH N H.Optimal orbit transfer of a spacecraft with fixed length tether［J］.Journal of the Astronautical Sciences，2003，51(2):195-204.

［9］SUN L，ZHAO G W，HUANG H.Stability and control of tethered satellite with chemical propulsion in orbital plane［J］.Nonlinear Dynamics，2013，74:1113-1131.

［10］LIU H T，YANG L P，ZHANG Q B，et al.An investigation on tether-tugging de-orbit of defunct geostationary satellites［J］.SCIENCE CHINA Technological Sciences，2012，55(7):2019-2027.

［11］ASLANOV V S，YUDINTSEV V.Dynamics of Large Debris Connected to Space Tug by a Tether［J］.Journal of Guidance Control and Dynamics，2013，36(6):1654-1661.

［12］ASLANOV V S，LEDKOV A S.Dynamics of towed large space debris taking into account atmospheric disturbance［J］.Acta Mech，2014，225:2685-2697.

［13］ASLANOV V S，YUDINTSEV V.Dynamics，analytical solutions and choice of parameters for towed space debris with flexible appendages［J］.Advances in Space Research，2015，55:660-667.

［14］BISCHOF B，KERSTEIN L，STARKE J，et al.Roger-Robotic geostationary orbit restorer［C］//54thInternational Astronautical Congress of the International Astronautical Federation(IAF).Bremen，Germany，2003.

［15］ASLANOV V S，YUDINTSEV V V.The motion of tethered tug-debris system with fuel residuals［J］.Advances in Space Research，2015，56:1493-1501.

Dynamics of Tether Tugging Deorbiting System in the Presence of Offset

LIU Helong1，2，HE Yingzi1，2，TAN Shuping1，2
(1.Beijing Institute of Control Engineering，Beijing 100190，China; 2.Science and Technology on Space Intelligent Control Laboratory，Beijing 100194，China)

The dynamical characteristics of tether tugging deorbiting system after the capture by net or gripper are focused on.The modeling and simulation about a simplified configuration in the presence of offset are studied.The combination after capture consists of space tug，tether and space debris.A simplified configuration is proposed，whose attachment point of tether on space debris is viewed as a fixed offset.Then，taking the descending process as an example，the energy equation is given and the dynamic equations of the system are formulated based on Euler-Lagrange method.The equilibrium point is obtained under proper assumption that the tether is tight.At last，the dynamical characteristics of the system are analyzed with different initial angular velocities when tether is tight or slack.The results demonstrate that a safe deorbiting can be guaranteed when the initial angular velocity of the object satellite is small，and when the initial tether is either tight or slightly slack.

tether tugging;offset;safe deorbiting

V471+.6

A

1674-1579(2017)01-0042-07

10.3969/j.issn.1674-1579.2017.01.007

刘贺龙(1988—)，男，博士生，研究方向为空间操作;何英姿(1970—)，女，研究员，研究方向为控制理论与控制工程;谈树萍(1978—)，女，高级工程师，研究方向为控制理论与控制工程.

*国家自然科学基金资助项目(61304037).

2016-00-00