日地平动点编队飞行自抗扰轨道维持控制

姜春生，王 永，李恒年，楼张鹏

(1.宇航动力学国家重点实验室，西安710043;2.中国科学技术大学自动化系，合肥230027)

日地平动点编队飞行自抗扰轨道维持控制

姜春生1，2，王 永2，李恒年1，楼张鹏2

(1.宇航动力学国家重点实验室，西安710043;2.中国科学技术大学自动化系，合肥230027)

对日地平动点附近的航天器编队控制问题进行研究，为解决基于局部线性化模型设计轨道保持控制器时存在的控制精度不高、模型精确性过度依赖等问题，提出基于圆型限制性三体问题的日-地/月系统L2点附近主从式航天器编队飞行的相对位置控制问题的解决方法.将主航天器设定在Halo轨道上，从航天器利用自抗扰控制方法控制在主航天器周围，编队系统内的未知动力学和外部扰动由扩张状态观测器获得，并利用非线性误差反馈对其进行补偿.数值仿真结果显示采用0.1 μN到10 mN的控制力即可使航天器相对位置误差控制在位置精度要求范围内，同时在存在未知干扰的情况下该方法依然具有很好的鲁棒性，从而验证优越性.

航天器编队飞行;主从编队;圆型限制性三体问题;平动点轨道;自抗扰控制

0 引言

近年来随着人类探索太空的步伐逐渐加快，平动点轨道已经成为空间科学的研究热点，其魅力在于平动点附近存在复杂的空间环境、轨道的不变流形、同/异宿连接等特殊现象，以及它们在轨道设计和分析中的重要应用价值.特别地，在日地系统L2点附近没有大气、空间碎片、地球红外辐射、重力梯度和地球磁场等干扰，是宇宙观察和天文研究的理想场所［1］.

航天器编队是指一组航天器以某种构形保持在空间轨道以协同完成航天飞行任务［2］.与单一航天器不同，航天器编队具备更高的任务灵活度，且受单个航天器故障影响更小.目前国外在研的航天器编队飞行任务有Micro Arcsecond X-Ray Imaging Mission［3］、PRISMA［4］、the QB50 mission［5］及Proba-3［6］等.

编队控制作为关乎航天器编队飞行成功与否的关键问题之一，成为很多航天学者的研究重点.其中应用最为广泛的即处理编队系统动力学问题的Clohessy-Wiltshire(C-W)方程.许多学者基于C-W模型提出了不同的线性控制技术，如Kapila［2］，Joshi和Padhi［7］，Mu等［8］以及Wang等［9］利用LQR方法研究了编队飞行的控制问题.除此之外，Luquette等［10］利用反馈线性化设计了控制算法以实现对六自由度航天器编队中飞行器的位置和姿态控制.文献［11］中对现有的线性编队控制策略进行了深入调研.

由于线性控制方法只有在特定条件下才能获得良好的控制效果，且近年来深空编队飞行任务的精度要求逐步提高，相对位置精度要求达到了亚毫米级，因此大量的研究开始关注非线性控制策略.Gurfil等［12］提出了一种用于深空任务的自适应神经网络控制器.Wang等［13］提出一种日-地/月L2点附近编队飞行的自适应控制器.Infeld等［14］把编队飞行控制当作一种非线性有约束最优控制问题来处理.Peng等［15］提出了一种用于航天器轨道保持和编队飞行的最优周期控制器.Wang等［16］设计了基于多项式特征结构的日-地/月L2点附近的非线性编队保持控制器.此外，Bae和Kim［17］将滑模控制技术应用于航天器编队控制.Darvish等［18］利用非线性积分滑模控制和最优闭环LQR方法研究了Halo轨道控制以及航天器精确编队重构等问题.

上述非线性方法都获得了较好的控制效果.然而，这些方法都严重依赖于复杂的动力学模型，而当系统存在不确定性和扰动时会降低系统的鲁棒性.为了解决这类问题，本文提出了一种基于自抗扰控制(active disturbance rejection control，ADRC)的非线性编队飞行控制策略.ADRC由Han［19-20］最先提出，其基本思想是利用扩张状态观测器来估计系统的动力学特性和外部扰动以及不确定性，并利用状态误差反馈控制对其进行补偿.与现有基于精确模型的方法不同，ADRC对系统动力学的信息依赖很少，其算法简单，参数易于调节，且对于系统扰动具有鲁棒性.由于其良好的鲁棒性和抗干扰能力，该方法非常适合于解决航天器编队飞行的控制问题.

本文考虑一种带有三个从航天器的主从式编队飞行方案:假设主航天器运行于日-地/月L2点附近的Halo轨道上，控制从航天器与主航天器保持1 km的距离且等距分布在主航天器周围构成一个圆.文中考虑了太阳光压和地球轨道偏心率影响产生的外部扰动等以检验所设计控制器的鲁棒性.最后，将本文结果与文献［15］中的结果对比，验证了本文所提方法的有效性和优越性.

1 系统模型

1.1 圆型限制性三体问题

本文主要考虑在日-地/月系统L2点附近的Halo轨道上航天器的主从式编队控制问题，基于圆型限制性三体问题(circular restricted three-body problem，CRTBP)模型，定义质心旋转坐标系O-XYZ，其中，两个大天体质心为坐标原点O，X轴从太阳指向地月的质心，Z轴垂直于黄道面，Y轴与X轴，Z轴构成右手坐标系，如图1所示.用m1代表太阳质量，m2代表地球和月球质量之和，m代表航天器质量，m≤m1，m≤m2.两个大天体绕它们的质心在黄道面内以角速度Ω做圆周运动.为分析问题和计算上方便，定义两个大天体之间距离为单位长度AU，1/Ω为单位时间TU，两大天体质量之和为单位质量.记R=［X Y Z］T为航天器在旋转坐标系下的位置矢量，则CRTBP动力学方程为

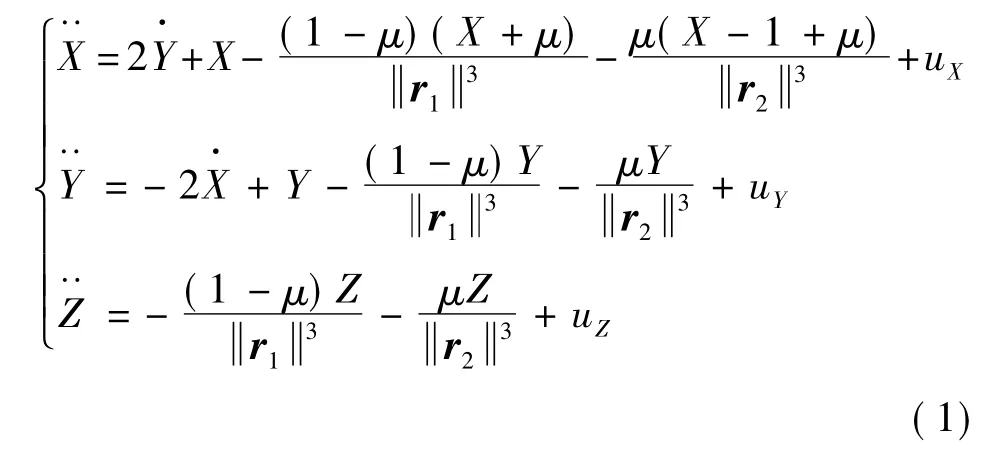
式中:u=［uXuYuZ］T为控制矢量，μ=r1=［X+μ Y Z］T;r2=［X-1+μ Y Z］T.

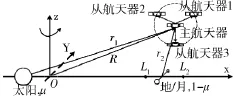
图1 CRTBP几何构型及航天器编队Fig.1 Geometry of CRTBP and spacecraft formation

1.2 编队系统相对运动方程

在CRTBP中，主、从航天器的动力学方程都可用式(1)表示.假设在旋转坐标系下主，从航天器的位置矢量分别为rl=［xlylzl］T，rf=［xfyfzf］T，则从航天器相对主航天器的位置矢量为

记r=［x y z］T，利用式(1)～(2)可得，从航天器相对主航天器的运动方程为

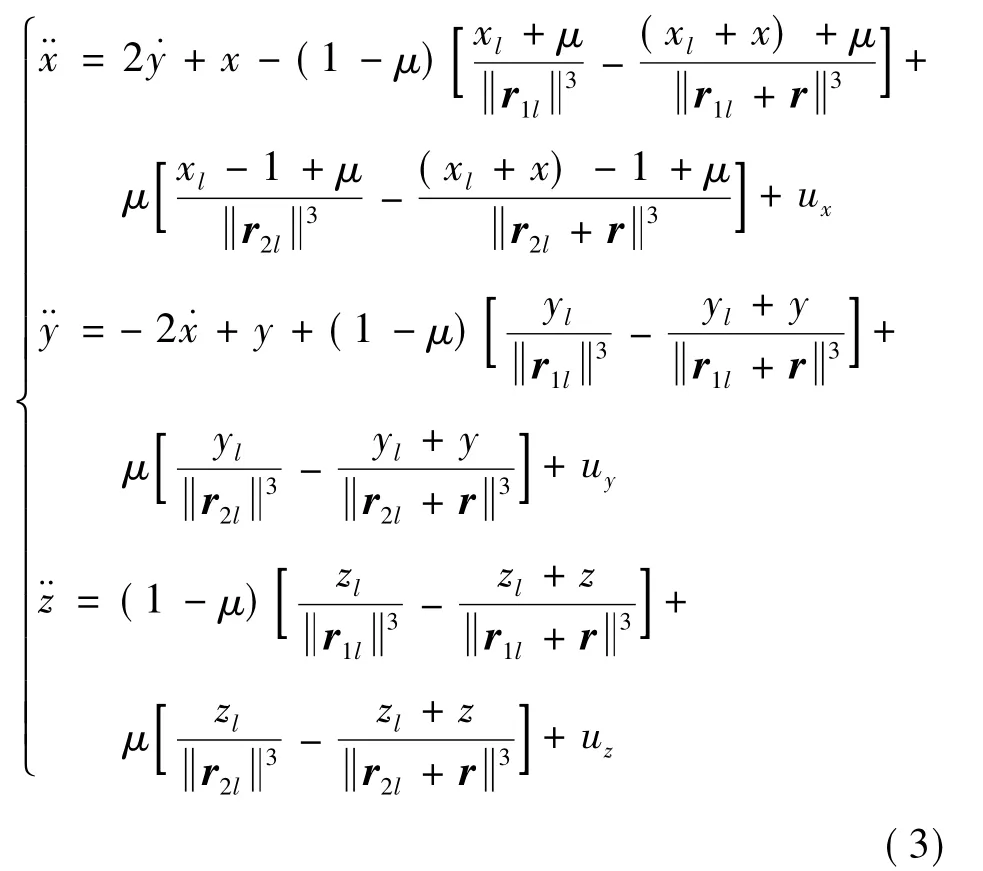
式中:ux=ufx-ulx;uy=ufy-uly;uz=ufz-ulz为控制输入.

1.3 扰动

在深空环境中存在着很多外力干扰，例如地球轨道偏心率，太阳光压力和其他天体的引力等，其中地球轨道偏心率和太阳光压力的影响尤为显著.本文考虑地球轨道偏心率和太阳光压力的影响产生的扰动来验证所设计控制器的抗干扰能力.

(1)地球轨道偏心率

航天器单位质量所受地球轨道偏心率影响产生的扰动可近似表示为［21］

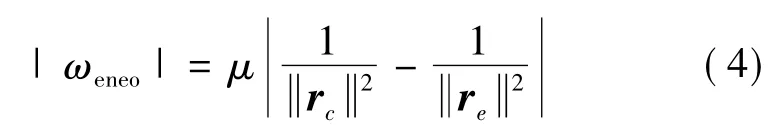
式中:re是由平动点指向地球椭圆轨道的近中心点的位置矢量;rc是平动点指向圆轨道圆心的位置矢量.

(2)太阳光压力

根据文献［12，22］中给出的模型，由太阳光压力产生的干扰加速度为

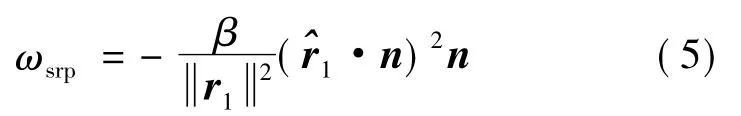
2 自抗扰控制

ADRC是一种基于系统输入输出而不依赖系统模型的控制方法，能够有效解决线性化方法设计控制器时带来的近似范围约束、模型依赖性强等问题.本文设计的ADRC结构如图2所示.图中:xref为给定参考信号;xt为根据参考信号安排的过渡过程;vx是xt的微分;ux0是误差状态反馈控制量;ux为经过扰动补偿后的最终控制量.ADRC主要由跟踪微分器、扩张状态观测器和非线性状态误差反馈3部分组成.

图2 ADRC结构图(X轴方向)Fig.2 Structure of the ADRC(in X direction)

首先利用非线性跟踪微分器(tracking differentiator，TD)为系统安排过渡过程从而解决系统超调与响应速度间的矛盾，同时提供微分信息.然后利用扩张状态观测器(extended state observer，ESO)跟踪系统动态特性和未知扰动，并且进行实时补偿.最后通过非线性状态误差反馈(nonlinear state error feedback，NSEF)获得系统控制输入.为叙述简洁起见，本文只介绍X轴方向的控制律设计，Y，Z轴方向与X轴形式相同.

2.1 跟踪微分器

TD用来跟踪给定的编队结构，给定参考信号xref，根据参考信号安排过渡过程xt，并提取其微分信号vx.离散形式的TD设计如下:

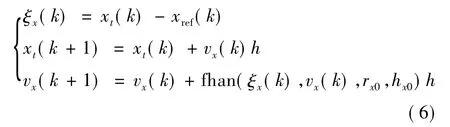
式中h为步长.式(6)有两个可调参数rx0，hx0.rx0决定跟踪速度，称作“速度因子”;hx0对噪声起滤波作用，称作“滤波因子”.fhan(ξ，v，r0，h0)的具体表达如下［23］:

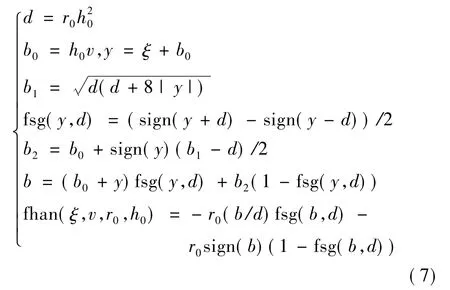
2.2 扩张状态观测器

将X轴方向相对运动方程表示如下:

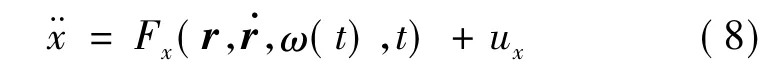
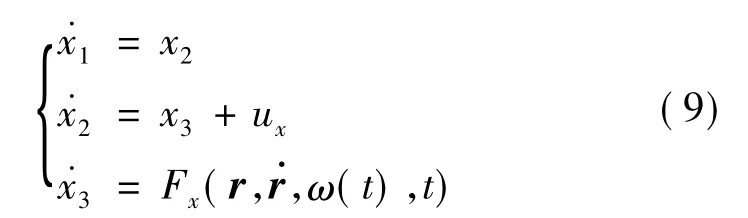
根据参考文献［23］，ESO设计如下:

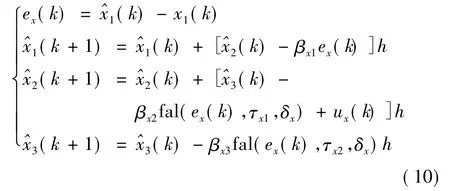
式中:βx1，βx2，βx3，τx1，τx2，δx均为ESO的可调参数，非线性函数fal(·)形式为

2.3 NSEF控制律

由于ESO已经估计出系统状态，将系统状态误差进行反馈即可设计控制律.函数fhan具有快速跟踪对象状态和消除抖振的特殊能力，因此本文用它来进行自抗扰控制器中的误差的非线性组合.设计误差反馈控制律为［23］

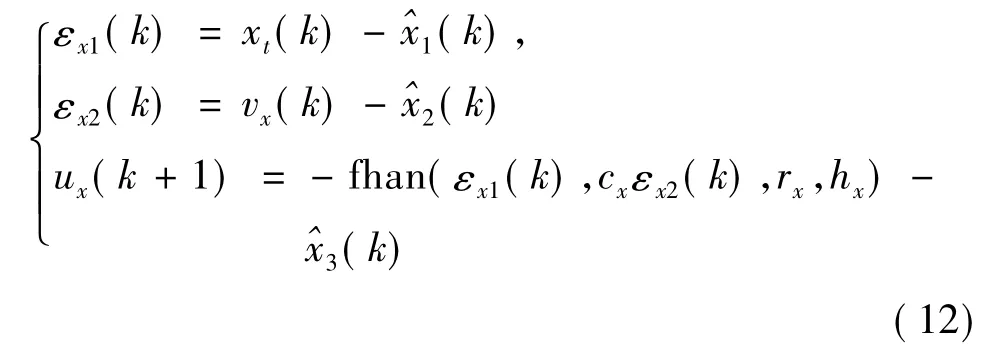
式中cx为阻尼因子.

3 数值仿真

为了验证所提出的ADRC方法，本节对第1节给出的运动方程和第2节提出的控制策略进行了数值仿真.仿真时间设定为3年，取采样步长 h= 0.000 1 TU.ADRC方法的相应参数在表1中给出.

表1 ADRC方法参数Tab.1 Parameters of the ADRC method

假设主航天器运行在日-地/月L2点的Halo轨道附近，Halo轨道幅值为1.2×105km，如图1所示.假设从航天器相对于主航天器的初始位置和速度为0.从航天器的期望相对位置在表2中给出.

表2 从航天器期望相对位置Tab.2 Desired relative positions of three followers

图3～5显示了对3个从航天器的编队控制结果.如图3(a)所示，从航天器1的X，Y，Z轴方向的误差在两天的时间内很快下降到0，然后在0附近周期变化，并且其稳态误差保持在微米级.图3(b)显示了X轴方向和Y轴方向推进器最初需提供10 mN的力以维持稳定，但在一天的时间内该推进力很快下降到小于0.1 μN.图4和图5则展示了从航天器2和3的编队控制结果，如图所示，所有的相对位置误差都保持在微米级，同时推力被控制在小于0.1 μN范围内.

此外，本文将ADRC控制器与Peng等［15］设计的最优周期控制器(optimal periodic controller，OPC)控制效果进行比较，结果如表3所示.根据表3可以看出，用ADRC和OPC方法控制的位置误差绝对值两种方法分别为4.378 μm和4 736.9 μm.从航天器2，3的结果类似，这也表明了ADRC控制器的控制效果优于OPC控制器.

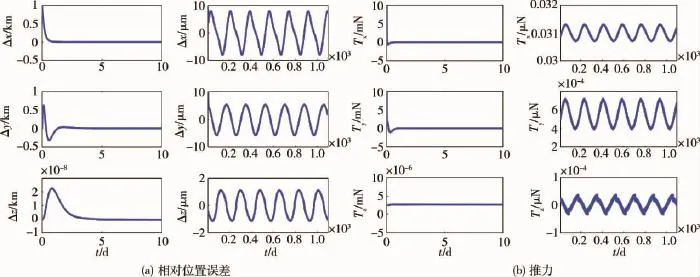
图3 从航天器1编队控制结果Fig.3 Formation control results of follower 1

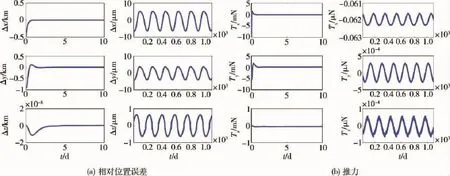
图4 从航天器2编队控制结果Fig.4 Formation control results of follower 2

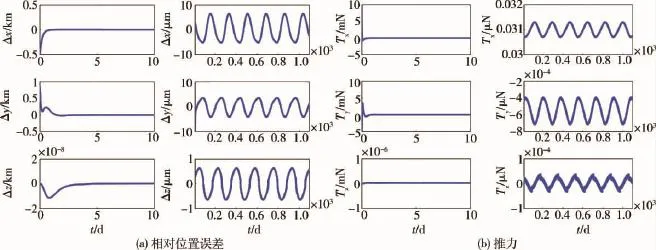
图5 从航天器3编队控制结果Fig.5 Formation control results of follower 3

表3 OPC和ADRC控制器的相对位置误差绝对值Tab.3 The mean absolute values of relative errors of ADRC and OPC

4 结论

本文针对存在系统不确定性、初始误差和外界扰动的多航天器编队飞行的相对位置控制问题提出了自抗扰控制方法.该方法仅需要知道每个航天器的位置信号，定义编队系统的不确定性和地球偏心率和太阳光压力为总扰动，利用扩张状态观测器进行实时估计，利用非线性状态误差反馈控制律实时地动态补偿这些扰动.通过将数值仿真的结果与现有控制方法进行比较，表明了利用ADRC控制方法可以满足精度要求下更好地抵御未知干扰.总而言之，所提出方法具有有效性并且有望推广于其他的平动点和轨道.

［1］XU M，LIANG Y，REN K.Survey on advances in orbital dynamics and control for libration point orbits［J］.Progress in Aerospace Sciences，2016，82:24-35.

［2］KAPILA V，SPARKS A G，BUFFINGTON J M，et al.Spacecraft formation flying:dynamics and control［J］.Journal of Guidance，Control，and Dynamics，1999，6 (3):4137-4141.

［3］GENDREAU K C，CASH W C，SHIPLEY A F，et al.MAXIM pathfinder X-ray interferometry mission［C］//Astronomical Telescopes and Instrumentation.International Society for Optics and Photonics.Washington D.C.:SPIE，2003.

［4］D’AMICO S，ARDAENS J S，LARSSON R.Spaceborne autonomous formation-flying experiment on the PRISMA mission［J］.Journal of Guidance，Control，and Dynamics，2012，35(3):834-850.

［5］GILL E，SUNDARAMOORTHY P，BOUWMEESTER J，et al.Formation flying within a constellation of nanosatellites:The QB50 mission［J］.Acta Astronautica，2013，82(1):110-117.

［6］ARDAENS J S，D’AMICO S，CROPP A.GPS-based relative navigation for the Proba-3 formation flying mission［J］.Acta Astronautica，2013，91:341-355.

［7］JOSHI G，PADHI R.Robust satellite formation flying through online trajectory optimization using LQR and neural networks［J］.IFAC Proceedings Volumes，2014，47(1):135-141.

［8］MU J，GONG S，LI J.Coupled control of reflectivity modulated solar sail for GeoSail formation flying［J］.Journal of Guidance，Control，and Dynamics，2014，38 (4):740-751.

［9］WANG F，NABIL A，TSOURDOS A.Centralized/decentralized control for spacecraft formation flying near Sun-Earth L2point［C］//The 4thIEEE Conference on Industrial Electronics and Applications.New York: IEEE，2009:1159-1166.

［10］LUQUETTE R J，SANNER R M.A nonlinear，six-degree of freedom，precision formation control algorithm，based on restricted three body dynamics［J］.Advances in the Astronautical Sciences，2003，113:105-114.

［11］KRISTIANSEN R，NICKLASSON P J.Spacecraft formation flying:a review and new results on state feedback control［J］.Acta Astronautica，2009，65(11-12):1537-1552.

［12］GURFIL P，IDAN M，KASDIN N J.Adaptive neural control of deep-space formation flying［J］.Journal of Guidance Control and Dynamics，2003，26(3):491-501.

［13］WANG F，LIU M，JIN R，et al.Adaptive backstepping controller and sliding mode controller design for formation flight in Sun-Earth L2point［J］.Aerospace Science and Technology，2016.

［14］INFELD S I，JOSSELYN S B，MURRAY W，et al.Design and control of libration point spacecraft formations［J］.Journal of Guidance Control and Dynamics，2007，30(4):899-909.

［15］PENG H J，ZHAO J，WU Z，et al.Optimal periodic controller for formation flying on libration point orbits［J］.Acta Astronautica，2011，69(7):537-550.

［16］WANG F，CHEN X Q，TSOURDOS A，et al.Sun-Earth L2point formation control using polynomial eigenstructure assignment［J］.Acta Astronautica，2012，76 (4):26-36.

［17］BAE J，KIM Y.Adaptive controller design for spacecraft formation flying using sliding mode controller and neural networks［J］.Journal of the Franklin Institute，2012，349(2):578-603.

［18］DARVISH K，POURTAKDOUST S H，ASSADIAN N.Linear and nonlinear control strategies for formation and station keeping of spacecrafts within the context of the three body problem［J］.Aerospace Science and Technology，2015，42(7):12-24.

［19］HAN J Q.Control theory，is it a model analysis approach or a direct control approach［J］.Journal of System Science and Mathematical Sciences，1989，9(4): 328-335.

［20］HAN J Q.From PID to active disturbance rejection control［J］.IEEE Transactions on Industrial Electronics，2009，56(3):900-906.

［21］KULKARNI J E，CAMPBELL M E，DULLERUD G E.Stabilization of spacecraft flight in halo orbits:an h∞approach［J］.IEEE Transactions on Control Systems Technology，2006，14(3):572-578.

［22］MCINNES C R，MCDONALD A J C，SIMMONS J F L，et al.Solar sail parking in restricted three-body systems［J］.Journal of Guidance Control and Dynamics，1994，17(2):399-406.

［23］韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2008.

ADRC-Based Orbit Maintaining Control of Spacecraft Formation Flying Around Halo Orbits About the Sun-Earth Libration Points

JIANG Chunsheng1，2，WANG Yong1，LI Hengnian2，LOU Zhangpeng1
(1.State Key Laboratory of Astronautic Dynamics，Xi’an 710043，China; 2.Department of Automation，University of Science and Technology of China，Hefei 230027，China)

The problem of relative position control is addressed for spacecraft formation flying around the Sun-Earth/Moon L2libration point.In order to avoid the problem of low precision and dependence on accurate model which occurs when controllers are designed according to linearized models，a relative position control technique is proposed that utilizes the framework of the circular restricted three-body problem.Assuming that the leader spacecraft is in a fixed halo orbit，the position of each follower relative to the leader is controlled to approach to a constant via using the active disturbance rejection control method.In this method，the unknown dynamics and external disturbances of the formation flying system are estimated by an extended state observer，which are compensated by a nonlinear state error feedback control law in real time.The numerical simulations show that the relative position errors obtained by the proposed method are all within the demanding range using the thrust from 0.1 μN to 10 mN.Meanwhile，the proposed method has good robustness against unknown disturbances and shows the superiority in control technique.

spacecraft formation flying;leader/follower formation;circular restricted three-body problem;libration point orbits;active disturbance rejection control

V412.4

A

1674-1579(2017)01-0049-06

10.3969/j.issn.1674-1579.2017.01.008

姜春生(1990—)，男，硕士研究生，研究方向为航天器轨道学与控制的研究;王 永(1962—)，男，教授，研究方向为运动体控制，振动主动控制，飞行器制导与控制，机器人控制，信息融合等研究;李恒年(1967—)，男，研究员，研究方向为航天器轨道姿态动力学与控制，航天器地面测控等研究;楼张鹏(1990—)，男，博士研究生，研究方向为航天器轨道学与控制的研究.

2016-12-01