基于自适应算法的Stewart平台微振动低频激励控制研究

许翔鹏，黄 海，黄 舟

(1.北京航空航天大学，北京100191;2.中国工程物理研究院总体工程研究所，绵阳621999)

基于自适应算法的Stewart平台微振动低频激励控制研究

许翔鹏1，黄 海1，黄 舟2

(1.北京航空航天大学，北京100191;2.中国工程物理研究院总体工程研究所，绵阳621999)

针对空间微振动环境模拟的需求，以Stewart平台为对象，研究低频微振动激励控制.传统定增益控制器需要反复调节参数来获取满意的系统输出，同时由于摩擦等因素引起的非线性现象，导致难以在低频段建立精确的系统模型，以上问题均给控制器的设计带来困难.为此，设计一种自适应控制器加传统PID控制器的控制方案，并针对自适应控制器对于非参数不确定性等因素敏感的问题，采用dead-zone技术对自适应律进行修正，以提高控制器的鲁棒性.将此算法应用于Stewart微激励控制系统中，实验结果表明系统平台可以很好的输出单自由度与多自由度低频正弦激励，验证控制器在实际工程中的有效性.

自适应控制器;鲁棒性;Stewart平台;低频激励

0 引言

随着相机、望远镜、传感器等精密星载设备精度要求的不断提高，太空环境中的微振动干扰对于星载精密设备的影响越来越受到工程界的重视.研究表明［1］在太空微重力的环境存在大量低频的微振动现象，振动频率主要分布在0.1～10 Hz之间，特别在1 Hz附近的振动量级可以到达10 mg左右，因此在星载设备发射到太空之前，对设备进行微激励低频实验十分必要.振动实验多采用单轴激励方式，但是在实际工作中，星载设备受到的振动是多自由度的，单轴振动实验并不能有效模拟太空振动环境.多轴振动实验对于星载精密仪器是更为有效的评价手段，但中国由于缺少实验设备、试验方法以及相应的试验规范，多轴振动实验尚未纳入航天器设计和验证流程［2］.因此，研制多自由度微激励系统平台以及相应的振动控制算法具有重要意义.

Stewart平台是一种六自由度并联机构，具有定位精度高、刚度大、承载能力强、动态性能好等特点，被广泛应用于工程中的各个领域［3］.美国空军实验室的高频振动台［4］及MTS公司的 Model 353振动台均采用了Stewart构型.这类平台具有多轴运动的能力，能够同时产生六自由度的振动信号，可以更好地模拟精密设备的振动环境.对于Stewart多自由度微激励系统，如何有效控制其产生期望的振动信号是研究的重点.国内外学者在激振平台的控制方面进行了大量研究，三参量控制(three variable control，TVC)是控制激振台的一种方法，其中“三参量”代表振动台的位移、速度和加速度，三参量控制可以分为前馈部分和反馈部分，两部分的增益可以独立调节［5］.1984年，日本三菱公司成功研制出6m×6m的三向六自由度大型地震台，首次采用三参量控制方法实现了液压振动试验系统的加速度控制，之后该方法便得到了广泛的应用，但这种算法需要对其中的六个参数反复手动调节，使用时比较不便.幅值相位控制是一种自适应控制方法，可实现对正弦信号幅值和相位的跟踪，这种方法以一个正弦信号和它的一个90°相角延时信号的加权和作为输入信号，将误差反馈到一个最小均方(LMS)控制器中以调节权系数，最终使这个误差趋于零，但是此种方法只有一个权系数可调，系统的收敛过程较慢［6］.

基于以上控制问题，本文提出了一种多个参数可调的自适应控制器，该控制器不需要任何关于模型的先验知识同时又不需要反复手动调节增益参数，通过在线的实时适应使系统输出信号与参考信号一致.最后在多自由度微激励控制系统中进行实验验证，实验表明该控制器对于多自由度微激励控制系统有着良好的控制效果，验证了该控制器在实际工程中的有效性.

1 控制器的设计

微激励振动台低频控制中存在着摩擦等非线性因素的干扰，增加了控制器设计的难度.实际工程中系统的动力学特性通常是随时间变化的，在控制过程中系统可能会出现参数的变化，传统定增益控制无法处理好此类问题.除此之外，很多控制器的设计过程需要建立精确的系统模型，工程实际难以实现.为了解决上述问题，本文设计自适应控制器加传统PID控制器的控制方案，该方案不需要任何关于系统的先验知识，并且在实验过程中不需要调节任何控制参数.

本文设计的控制器由自适应控制器和传统PID控制器两部分构成.其中，自适应控制器的控制律为

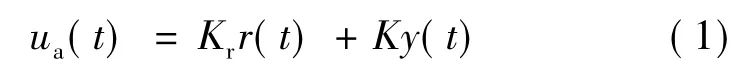
式中ua(t)为自适应控制器的控制信号，Kr，K为自适应增益系数，r(t)为输入信号，y(t)为输出信号，参考模型可为一阶系统或二阶系统，本文进行了进一步简化将模型取为单位1，自适应控制器结构如图1所示.

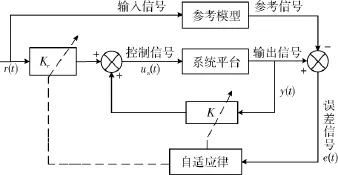
图1 自适应控制器结构图Fig.1 The structure of the adaptive controller

定理1.如果两个信号e与φ建立如下动力学关系:

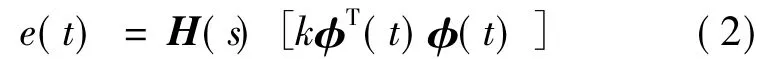
式中，e(t)为标量输出信号，H(s)是一个严格正定的传递函数，k是一个知道正负的常数，φ(t)是m×1关于时间的向量函数，v(t)是m×1的观测向量，如果向量φ如式(3)变化

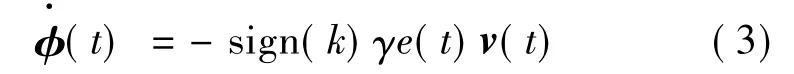
如果γ为正的常数，那么e(t)和φ(t)全局有界.如果v(t)也是有界的，那么当t→∞时，e(t)→0.

证明.用状态空间来表示动力学关系式(2)

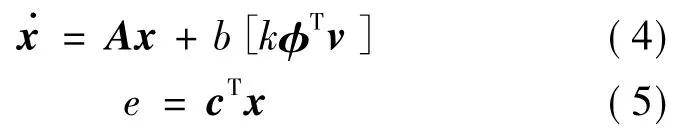
根据Kalman-Yakubovich引理可知，由于H(s)是严格正定传递函数，给定一个对称正定的矩阵Q，存在另一个对称正定矩阵P满足以下关系:

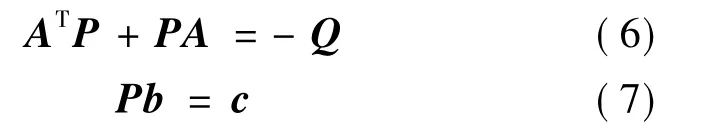
构造李雅谱诺夫函数

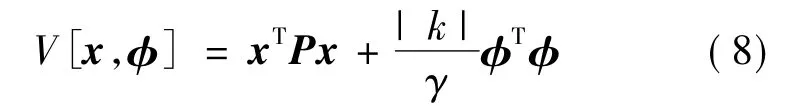
对式(8)求导可得

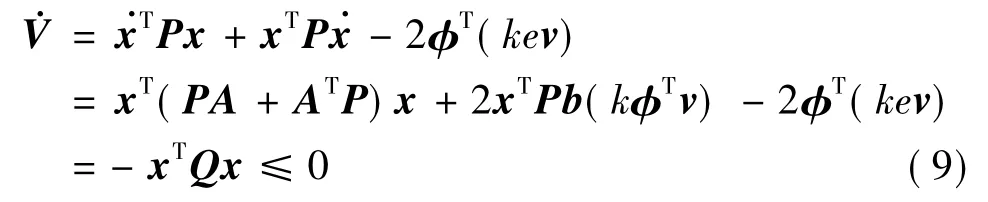
因此由式(1)～(2)定义的系统是全局稳定的，式(8)～(9)表明e和φ是全局有界的.

根据定理1本文的自适应律如式(11)

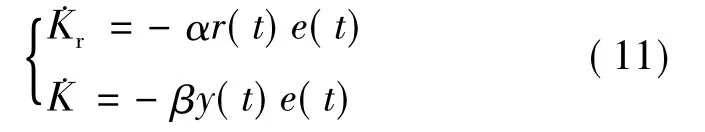
式中，Kr为输入信号的自适应增益系数，K为系统输出的自适应增益系数，α，β分别为自适应律中的增益系数.自适应律是针对连续系统设计的，但是在实际过程中需要将连续的自适应律转化成离散的自适应律，当系统采样频率很高时，可以将连续的自适应律直接应用到离散系统中.在实现的过程中可以通过数值积分的形式得到离散自适应律表达式，本文通过采用梯形积分公式得出自适应律的递推表达式如式(12)所示:

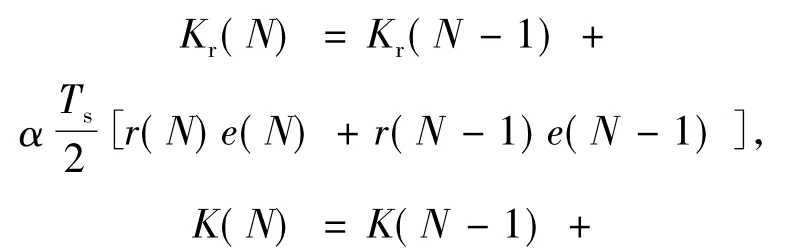
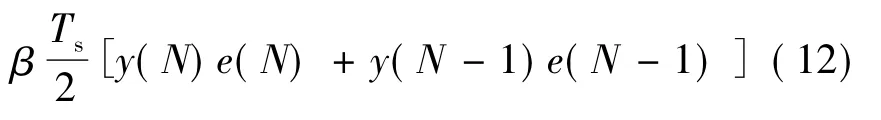
式中，N代表采样间隔，Ts为采样周期.除此之外，该控制算法的计算量较小，所以控制器的采样频率很高，可直接将离散的自适应律应用到实际控制器中.

自适应控制算法考虑的仅仅是参数不确定性，但是实际系统有着很多非参数不确定性因素，例如低频运动过程中的摩擦、传感器的观测噪声、计算的截断误差等.这些非参数不确定性因素会导致自适应控制器出现参数漂移的问题最终导致系统的突然发散.因此提高自适应控制器的鲁棒性是必须解决的问题，其中死区和σ-modification是提高控制器鲁棒性的两种措施［8-9］.本文采用了dead-zone技术对自适应律进行了修正，可以有效解决自适应控制器中参数漂移的问题，即给误差一个阈值，当误差绝对值小于Δ，自适应律不再更新，反之需要继续适应，修正后的自适应律如下.

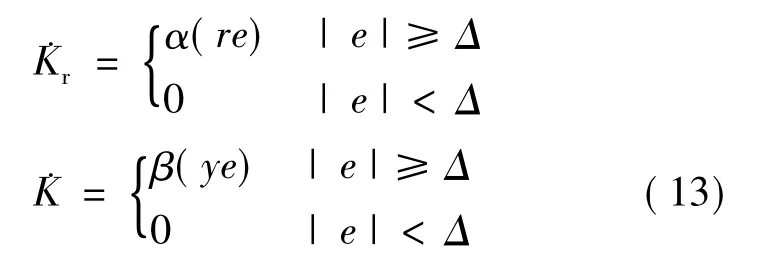
综上，本文设计自适应控制器的控制律如式(1)，自适应律如式(13)所示.除此之外本文又采取了自适应控制器与传统PID控制器结合的方式对系统进行控制如图2所示.

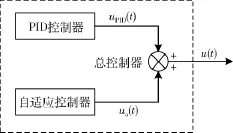
图2 控制器结构示意图Fig.2 The structure of the controller

因此总的控制律如(14)式所示

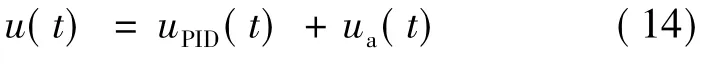
基于以上设计的控制器，本文进行了基于MATLAB/Simulink模型仿真，由于作动器系统采用位移传感器(linear variable differential transformer，LVDT)，故本作动器系统可以等效成一个二阶系统，仿真过程中的模型为二阶系统，其传递函数为

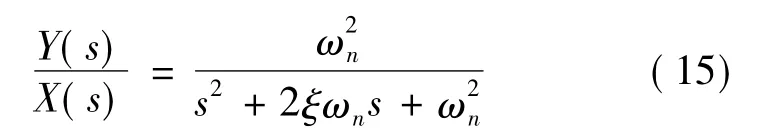
为了更好地表明本文控制器在解决模型参数不确定性上的优势，本文设计仿真系统的参数如下:其中ωn=40×π×(1±50%)，ξ=0.1×(1±50%)，参考信号为0.1～1 Hz以幅值1mm进行扫频，1～4 Hz幅值以频率平方衰减的形式进行扫频，同时在系统输出中加入少量白噪声信号用来模拟传感器中的观测噪声.在不改变控制器中任何参数的情况下，针对不同的仿真模型，均可以达到良好的控制效果，仿真结果表明控制器可以有效解决模型参数不确定性问题.仿真结果如图3，系统输出完全跟随上参考信号，误差的量级在0.01 mm之内，接近观测噪声的量级，表明该控制器对于二阶系统有着良好的控制效果.

图3 控制器仿真结果Fig.3 The simulation result of the control system

2 Stewart微激励平台的低频控制策略

Stewart平台最初由Gough引入，并作为轮胎测试实验的一部分，随后被Stewart进行了改进被用作了飞行模拟器平台［9］.Stewart平台具有多自由度、高精度、高刚度等优点，被应用于各个工程领域，主要用于飞行模拟器，并联机床，医疗机械，隔振台等领域.本文将Stewart平台作为微激励台进行控制，Stewart作为并联机构可以同时产生不同方向的振动激励.Stewart平台是一个多输入多输出系统(MIMO)，研究表明对于并联机器人运动学反解比运动学正解容易的多，通过运动学反解将上平台的运动转换到各个作动腿的运动，这样就把一个多输入多输出系统(MIMO)转换为单输入单输出系统(SISO).上平台的位移与各个作动腿作动位移之间的关系通过Jacobian矩阵的逆建立起来，具体如下:

其中，θ为各个作动腿的位移，σ为上平台的位移，J-1为Jacobian逆矩阵.Stewart平台的结构如图4所示，Jacobian逆矩阵的如下［10］:

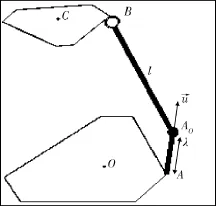
图4 Stewart结构图Fig.4 The structure of the Stewart platform

综上对于Stewart微激励系统的低频控制策略如图5所示，首先通过运动学反解将上平台的位移转换到各个作动腿上的位移，即将Stewart平台MIMO系统转换为SISO系统进行控制.

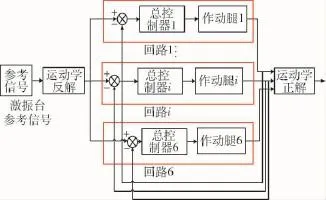
图5 Stewart平台低频控制策略Fig.5 The low-frequency control scheme of the Stewart platform

然后控制器通过安装在作动器上的LVDT位移传感器进行闭环控制，使传感器的输出跟随上作动腿的参考信号，如果位移传感器的输出能跟上其作动腿的参考信号，通过运动学正解(即将各个腿的作动位移转换到上平台的位移)，那么实际上平台的位移输出将跟随上激振台的参考信号.基于以上控制策略，通过Stewart微激励控制系统进行了实验，来验证控制策略的有效性.

3 实验结果

3.1 试验装置

Stewart微激励控制系统包括4部分:机械系统、气撑系统、控制硬件系统和控制软件系统.Stewart平台分为上下平台，中间通过6个作动器连接，整个机械系统如图6所示.

图6 Stewart机械系统Fig.6 The Mechanical system of the Stewart

气撑系统有3个辅助支撑和4个空气弹簧柔性支撑构成，主要是起平衡上平台及负载重量的作用.除此之外，音圈电机由于结构简单，响应快，频带高被应用于各个工程领域，本激励平台就采用音圈电机作为作动器.控制软件系统是基于Linux-Rati系统，通过此系统对平台进行实时控制.

由于本文研究的是低频激励控制，传感器为LVDT位移传感器，加速度传感器为高频控制提供测量信号，本文并不涉及.实验系统包括:Stewart机械平台，基于Linux-Rati系统工控机，音圈电机作动器，LVDT位移传感器，A/D、D/A转换卡等如图7所示.

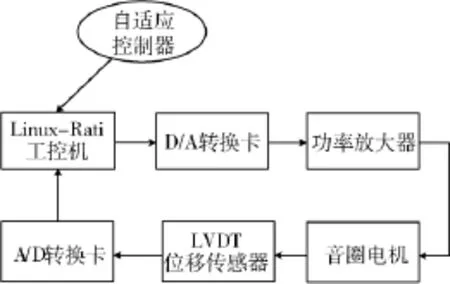
图7 实验控制系统结构图Fig.7 The structure of the experimental control system

3.2 试验结果分析

本文进行了如下工况实验:定频的单自由度正弦激励实验，定频的多自由度正弦激励实验，幅值随频率衰减的多自由度低频扫频实验.

工况1.振动方向为Z方向平动，参考信号是幅值为1 mm频率为1 Hz的正弦信号，实验结果如图8.图8(a)中的黑线代表Z方向平动的参考信号，粉线代表系统Z方向平动的输出信号，红线和蓝线分别代表 X方向平动和 Y方向平动上的输出信号，图8(b)3条线代表平台转动的输出信号.从图中可以看出系统Z方向平动输出信号能够很好的跟上参考信号，X和Y方向平动输出在0.01 mm左右，3个转动方向输出在0.05 mrad左右，非振动方向的误差几乎都达到了观测噪声的量级，实验结果表明控制器对于单自由度控制具有良好的效果.

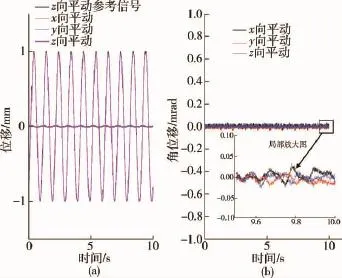
图8 Z向平动频率1 Hz的正弦激励结果Fig.8 The translational results of Z axes with 1 Hz sine signal

工况2.振动方向为多自由度分别是X方向平动、Z方向平动以及绕Z轴转动，X方向平动与Z方向平动的参考信号是幅值为0.375 mm频率为2 Hz正弦信号，绕Z方向转动的参考信号是幅值为1.5 mrad频率为2 Hz正弦激励.实验结果如图9所示，3个方向均可以有效的跟随参考信号，而其他非振动方向上的输出接近噪声量级，系统可以稳定的产生多自由度的正弦激励.

工况3.振动方向为Z方向平动和绕Z轴的转动，Z方向平动参考信号为0.1～1 Hz幅值为1 mm的扫频信号，在1～4 Hz为幅值随频率平方衰减的扫频信号.Z方向转动参考信号为0.1～1 Hz幅值为2 mrad的扫频信号，在1～4 Hz为幅值随频率平方衰减的扫频信号.实验结果如图10所示，图10(a)黑线为系统Z方向平动的参考信号，粉线为系统Z方向平动输出信号，可以看出系统可以很好的跟随参考信号.绕Z轴方向转动的实验结果如图10(b)所示，由此可知对于绕Z轴方向转动也有着良好的控制效果，实验结果表明控制器对于多自由度扫频激励也有着良好的控制效果.

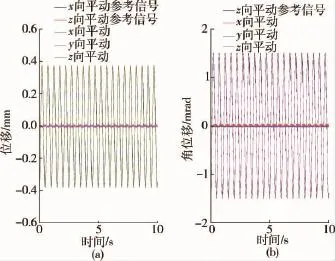
图9 X向平动、Z向平动及Z向转动2 Hz正弦激励结果Fig.9 The translational results of X axes and the translational and rotational results of Z axes with 2 Hz sine signal

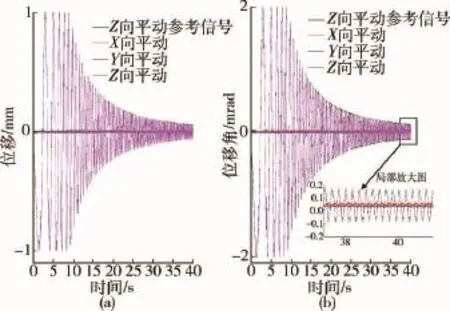
图10 Z向平动与Z向转动扫频结果Fig.10 The translational and rotational results of Z axes with sweep signal

根据以上实验结果可知，该方法对于Stewart微激励系统的低频控制有良好的控制效果，Stewart平台可以稳定地输出单自由度以及多自由度正弦激励信号，可以更好地模拟空间低频振动环境，具有重要的工程意义.

4 结论

本文为了更好地模拟精密设备在太空中的低频振动环境，对多自由度微激励平台进行了低频控制算法的研究.针对传统定增益控制器参数调节困难以及精确系统模型难以建立等问题，提出了一种在线实时调节参数的自适应控制器.文章中给出控制器的控制律以及自适应律，并采用死区技术对自适应律进行修正，有效解决了参数漂移问题，提高了控制器的鲁棒性.最后在Stewart平台上进行实验验证，实验表明该控制器能够使系统准确输出单自由度以及多自由度的低频正弦位移激励信号，证明了该控制器在实际工程应用中的有效性.

［1］GRODSINSKY C M，WHORTON M S.Survey of active vibration isolation systems for microgravity applications［J］.Journal of Spacecraft＆Rockets，1998，105(s 1-2): 146-152.

［2］次永伟，邱大芦，付乐平，等.航天器振动试验控制技术进展［J］.动力学与控制学报，2014(3):193-200.CI Y W，QIU D L，FU PL，et al.Progress in spacecraft vibration testing control technology［J］.Journal of Dynamics and Control，2014(3):193-200.

［3］STEWART D.A platform with six degrees of freedom［J］.Archive Proceedings of the Institution of Mechanical Engineers，2013，180(1965):371-386.

［4］EWING C.The advanced guided weapon testbed(AGWT)at the air force research laboratory munitions directorate［C］//AIAA Modeling and Simulation Technologies Conference，Washington D.C.:AIAA，2013.

［5］TAGAWA Y.Controller development for the E-Defense shaking table［J］.Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and control Engineering，2007，221(2):171-181.

［6］THOEN B K.Sinusoidal signal amplitude and phase control for an adaptive feedback control system［P］.US，US5124626，1992.

［7］SLOTINE J，JEAN-JACQUES E，LI W.Applied nonlinear control［M］.Englewood Cliffs，NJ:Prentice-Hall，1991.

［8］SERAJI H.Decentralized adaptive control of manipulators:theory，simulation，and experimentation［J］.IEEE Transactions on Robotics＆Automation，1989，5 (2):183-201.

［9］DASGUPTA B，MRUTHYUNJAYA T S.The Stewart platform manipulator:a review［J］.Mechanism＆Machine Theory，2000，35(1):15-40.

［10］MERLET J P.Parallel Robots［J］.Solid Mechanics＆Its Applications，2006，128:2091-2127.

Low-Frequency Control of Micro-Vibration Generation Using Stewart Platform Based on Adaptive Algorithm

XU Xiangpeng1，HUANG Hai1，HUANG Zhou2
(1.Beihang University，Beijing 100191，China; 2.Institute of Systems Engineering，China Academy of Engineering Physics，Mianyang 621999，China)

The Stewart platform is used to simulate the micro-vibration environment in space.The low-frequency control of micro-vibration generation is conducted based on the platform.The parameters are tuned repeatedly to get a satisfied performance of the system in the traditional fixed-gain controllers.Meanwhile，the nonlinear phenomenon caused by the friction makes it difficult to build an accurate system model.With the problems described above，it is difficult to design the controller for the system.To solve the problems，an adaptive controller is presented.Due to the sensitivity of non-parameter uncertainties，the dead-zone technique is used to modify the adaptive laws to improve the robustness.The algorithm is applied to the multi-degree micro-vibration excitation control system.The experimental results show that the platform can generate low-frequency sinusoidal signal excitations in both one-degree and multi-degree direction.The experimental results verify that the method is applicable for practical engineering problems.

adaptive controller;robustness;Stewart platform;low-frequency excitation

V448

A

1674-1579(2017)01-0036-06

10.3969/j.issn.1674-1579.2017.01.006

许翔鹏(1991—)，男，硕士研究生，研究方向为基于多自由度微激励系统的控制研究;黄 海(1963—)，男，教授，研究方向为飞行器结构优化，空间智能结构及其控制等;黄 舟(1991—)，男，助理工程师，研究方向为航天器振动试验设备结构设计.

2016-09-16