隐含条件“藏身”何处?

山东省枣庄市峄城区底阁中学(277300) 张运虎 ●

隐含条件“藏身”何处?

山东省枣庄市峄城区底阁中学(277300) 张运虎 ●

隐含条件是题设信息一种重要且常见的形式，能否发现并利用好题目中的隐含条件，常常成为能否顺利解题的关键因素．那么隐含条件到底身藏何处呢?

一、藏在基本概念、定义之中

例1 (2015年四川凉山州中考)已知实数m，n满足3m2+6m－5=0，3n2+6n－5=0，且m≠n，则

分析 由m≠n时，得到m，n是方程x2－2x－1=0的两个不等的根，根据根与系数的关系进行求解．

解 ∵实数m，n满足3m2+6m－5=0，3n2+6n－5 =0，且m≠n，则m，n是方程3x2+6x－5=0的两个不相等的根

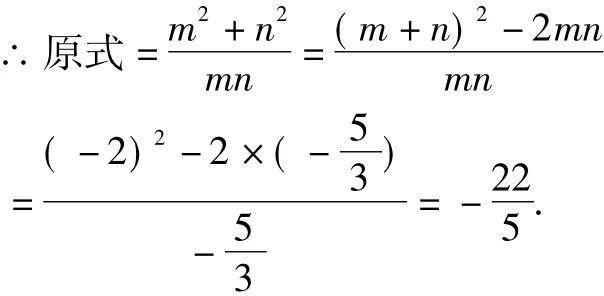
点评 本题根据m，n满足的条件，得知m，n是方程3x2+6x－5=0的两个不等的根是解题的关键．

二、藏在题设条件的特征之中

例2 已知当x=－2时，代数式 ax3+bx+1的值为6，那么当x=2时，代数式的值是___．

分析 ax3+bx+1是一个关于x的缺x2项的三次三项式，当x分别等于－2和2时，其中含a、b的两项必分别互为相反数，可采用整体消元法求值或整体代入法求值．

解 设x=2时，ax3+bx+1=M，

即8a+2b+1=M ①．

由已知，得－8a－2b+1=6 ②．

①+②，得2=M+6，∴M=－4，即ax3+bx+1=－4．

点评 数、式的特征中常常就包含着隐含条件，暗示着解题的思路和方向，这也是隐含条件最为普遍的藏身地．

三、藏在问题的简单或初始状态之中

例3 一位老师想辨别出他的三个聪明的学生A，B，C中哪一个更聪明．他采用的方法是:拿出5顶帽子，其中3顶是红的，2顶是黑的，让三个学生看了这5顶帽子以后，请他们闭上眼睛，然后分别给他们戴上1顶红帽子，并且把2顶黑帽子藏起来，最后请他们同时睁开眼睛，说出自己头上戴的帽子的颜色，但不能把帽子取下来看．过了一会儿，其中一个学生B，断定了自己头上戴的是红帽子，受到了老师的赞扬．请同学们想一想，他是怎样推断出来的?

分析 初见此题颇感为难，同学们有的抓头扰耳，有的争论不休，有的则不知所措，可见此题颇有挑战性．可是，如果我们能回到初始的状态，则会让人茅塞顿开，使问题迅速获解．可以从3顶帽子、两个人这个简单情况出发研究．3顶帽子，2红1黑，若给两个人分别戴上1红1黑，则戴上红的那个人一看到仅有的1顶黑帽子戴在对方头上，立即就能断定自己戴的是红帽子，但若给两人都戴上红帽子，每人眼里只看到对方戴的1顶红帽子，就难以断定自己头上戴的是哪种颜色的帽子，但两人中聪明的一个一定会想到，自己头上若是戴的黑帽子，那么对方立即就能说出头上戴的是红帽子，而现在对方在踌躇，所以自己头上戴的必定是红帽子．

现在来研究5顶帽子、3个人的情况．

B想如果自己头上戴的是黑帽子，那么剩下的人就成为4顶帽子(3红1黑)、两个人的问题，他们两个聪明人一定能通过上述考虑立即判断出自己头上所戴帽子的颜色而不会犹豫．现在他们在犹豫，那就说明我头上戴的是红帽子．

四、藏在一定的逻辑关系中

分析 结论没有用数学式子表示，很难直接证明，思维受阻．若能转换语言表达形式，即换一种说法，首先将结论用数学式子表示，转化成我们熟悉的形式．a，b，c中至少有一个等于1，也就是说a－1，b－1，c－1中至少有一个等于零，这样，问题就容易解决了．

于是(a－1)(b－1)(c－1)=abc－(ab+ac+bc)－1 +(a+b+c)=0，∴a－1，b－1，c－1中至少有一个等于0，即a，b，c中至少有一个等于1．

点评 数学就是一种逻辑的演绎，隐含条件常隐藏在一定的逻辑关系之中．因此，我们要注意掌握的运用逻辑分析和逻辑推理这个有力武器，让隐含条件暴露于光天化日之下．

五、藏在图形之中

例5 (2015年威海中考)如图1，已知 AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为( )

A．68° B．88°

C．90° D．112°

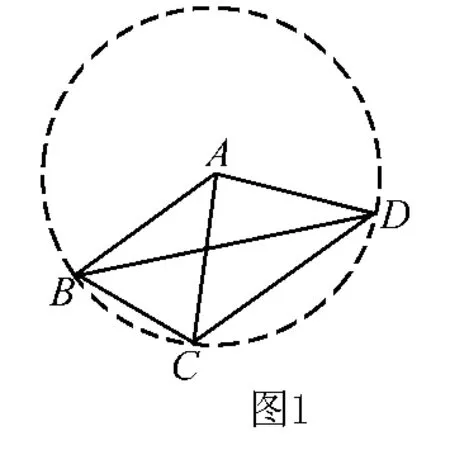
分析 如图，作辅助圆．首先运用圆周角定理证明∠CAD=2∠CBD，∠BAC=2∠BDC，结合已知条件∠CBD=2∠BDC，得到∠CAD=2∠BAC，即可解决问题．

解 如图，∵AB=AC=AD，∴点B、C、D在以点A为圆心，以AB的长为半径的圆上．∵∠CBD=2∠BDC，∠CAD=2∠CBD，∠BAC=2∠BDC，∴∠CAD=2∠BAC．而∠BAC=44°，∴∠CAD=88°，故选B．

点评 本题通过补出隐含在图形中的辅助圆，借助圆的性质使问题简捷、巧妙、迅速地获解．

G632

B

1008－0333(2016)32－0020－01