构造一元二次方程 巧求代数式的最值

山东省昌邑市柳疃初中(261302) 姜强柱 ●

构造一元二次方程 巧求代数式的最值

山东省昌邑市柳疃初中(261302) 姜强柱 ●

在数学竞赛中，我们经常会遇到求代数式的最值(最大值或最小值)问题，但被求最值的代数式又不是一般代数式，因而同学们都感到困难，觉的无从下手．对于这类问题，如果我们通过设元构造一元二次方程，或者根据题设条件利用根与系数的关系构造一元二次方程，利用一元二次方程的判别式便能巧妙的获解．下面举例说明．

(1993年全国初中数学联赛试题)

整理，得y2－10y+24=0，即(y－4)(y－6)≤0．

由题设知y≠6，所以解得4≤y＜6．

∵x为实数，∴Δ=(－y)2－4ay=y2－4ay≥0．

由于y＞0，所以y≥4a．

∴所求分式的最小值为4a．

例3 设a、b为实数，那么a2+ab+b2－a－2b的最小值是___．(1998年全国初中数学竞赛试题)

解 设a2+ab+b2－a－2b=y，将其整理成关于a的二次方程，得

a2+(b－1)a+(b2－2b－y)=0．

∵a为实数．

∴ Δ=(b－1)2－4(b2－2b－y)≥0．

∴4y≥3b2－6b－1=3(b－1)2－4≥－4，∴y≥－1．

故所求代数式的最小值是－1．

例4 已知x、y、z为实数，且x+y+z=5，xy+yz+zx =3．试求z的最大值与最小值．(2004年全国希望杯初中数学邀请赛竞赛试题)

解 由x+y+z=5，得y=5－x－z，代入xy+yz+zx =3，得x(5－x－z)+(5－x－z)z+zx=3．

将上式整理成关于x的二次方程，得x2+(z－5)x+ z2－5z+3=0．∵x为实数，

∴Δ=(z－5)2－4(z2－5z+3)≥0，即3z2－10z－13≤0．

例5 已知a、b均为实数，且满足a2+ab+b2=1①，则代数式的最大值与最小值的和___．

解 设a2－ab+b2=y②．

①+②，得2a2+2b2=1+y，即

由③、④可知a2、b2是二次方程(1－y)2=0的两个实数根．

整理，得3y2－10y+3≤0，即(3y－1)(y－3)≤0．

∴代数式a2－ab+b2的最大值是3，最小值是

故代数式a2－ab+b2的最大值与最小值的和是1

例6 已知p3+q3=2，其中p、q是实数，则p+q的最大值为___．(1987年江苏省初中数学竞赛题)

解 由p3+q3=2，得(p+q)(p2+q2－pq)=2．

(p+q)［(p+q)2－3pq］=2．

(p+q)3－3pq(p+q)=2．

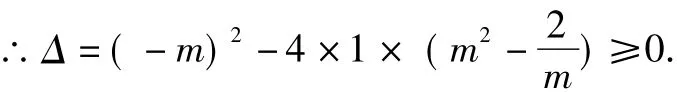
化简整理，得m3≤8，故m≤2，即p+q的最大值为2．

G632

B

1008－0333(2017)02－0015－01