基于IOWGA算子的江苏人均GDP的组合预测模型

涂洋，杨桂元

（安徽财经大学数量经济研究所，安徽 蚌埠 233000）

基于IOWGA算子的江苏人均GDP的组合预测模型

涂洋，杨桂元

（安徽财经大学数量经济研究所，安徽 蚌埠 233000）

选取1990—2009年江苏省人均GDP为样本数据，2010—2014年江苏省人均GDP作为验证数据，分别建立了ARIMA模型、指数平滑模型和多元回归模型对未来3年的江苏省人均GDP进行预测，然后在前3种单向预测方法基础上建立基于诱导有序加权几何平均（IOWGA）算子组合预测模型，再对此模型进行相应的效率评价.最后用组合预测模型对未来3年江苏省人均GDP进行预测.结果表明：相比于上述3种单项预测方法，基于IOWGA算子的组合预测模型的预测精度更高.预测结果表明2015—2017这3年，江苏人均GDP会继续增长，人民生活水平将继续提高.

IOWGA算子；组合预测模型；人均GDP

1 引言

人均GDP是体现一个国家或地区经济发展和生活水平的重要指标，不仅考虑到整体经济水平，还考虑到人口因素对经济的影响.相关统计数据显示，1990年江苏省人均GDP仅为2109元，而截止到2014年末江苏人均GDP已经增长到81874元，反映了二十多年来江苏省经济一直呈稳定上升趋势.那么未来几年江苏人均GDP是否像前二十多年一样仍呈一种快速增长的状态，需要建立模型进行预测.通过对未来的人均GDP的预测分析可以为政府制定地区经济目标提供参考，同时对政府解决因人民生活水平提高所引起的一系列社会问题提供一定帮助，这对于一个地区的经济发展和社会和谐都有重要意义.

目前，国内有许多有关江苏人均GDP的研究.例如陈海波［1］、陈洁［2］都通过ARIMA模型的建立预测了未来江苏人居GDP变化情况，结果表明未来江苏省人均GDP都将处于高速增长状态，江苏省经济仍然将保持一个快速发展的趋势.周慕鸿［3］基于SHTO理论，建立了SHTO（即江苏省住宅投资占GDP的百分比）与江苏人居GDP的多元回归模型，结果表明SHTO与江苏省人均GDP存在一种倒U型关系，并且预测出江苏人均GDP也将快速增长.上述研究成果对江苏人均GDP的预测都是建立单项预测模型.然而这些单项预测方法利用的数据信息较少，丢失的信息较多，因此预测的结果误差较大.比起单向预测方法，建立组合预测模型可以吸取各单向预测方法的优点，规避单向预测方法的缺点，提高预测精度.本文引入了诱导有序加权对几何平均（IOWGA）算子，建立组合预测模型对江苏人均GDP进行预测.

基于IOWGA算子的组合预测模型，国内许多学者已将其应用到各个领域.例如：王秋萍［4］在灰色预测模型和3次指数平滑模型两种单向预测方法的基础上建立了IOWGA组合预测模型对陕西省城镇居民人均可支配收入进行了预测.另外颜筱红［5］对我国能源消费的预测也建立了基于IOWGA算子的组合预测模型，其中选取的3种单项方法分别是趋势外推模型、GM（1，1）模型，3次指数平滑模型，结果表明组合预测模型是有效、可靠的.国内在对GDP的研究中也有选取该模型进行分析的.例如：莫颂娟［6］等人分别建立了回归与时间序列组合模型、ARIMA模型和GM（1，1）先对中国GDP总量进行预测，接着引入IOWGA算子，将3种单向预测方法组合起来对中国GDP总量进行预测，结果表明基于IOWGA算子组合预测模型明显比其他3种单向预测方法预测精度更高.

结合并参考上述相关基于IOWGA算子组合模型应用的参看文献，我们在预测江苏人均GDP时，首先分别选用了ARIMA模型、指数平滑法、多元回归模型3种单项预测模型，接着再引入诱导有序加权几何平均（IOWGA）算子，建立诱导有序加权几何平均组合预测模型对江苏人均GDP进行预测并对模型进行评价.最后用建立的组合预测模型对未来3年江苏省人均GDP进行预测.

2 江苏省人均GDP的单项预测

本文选取了1990—2009年江苏省人均GDP作为样本区间建立预测模型，将2010—2014江苏省人均GDP作为验证数据的区间，选择的变量有江苏省人均GDP、江苏省第三产业就业人数、江苏省预算财政支出，数据来自《江苏省统计年鉴》.

图1 1990—2009年江苏省人均GDP趋势图

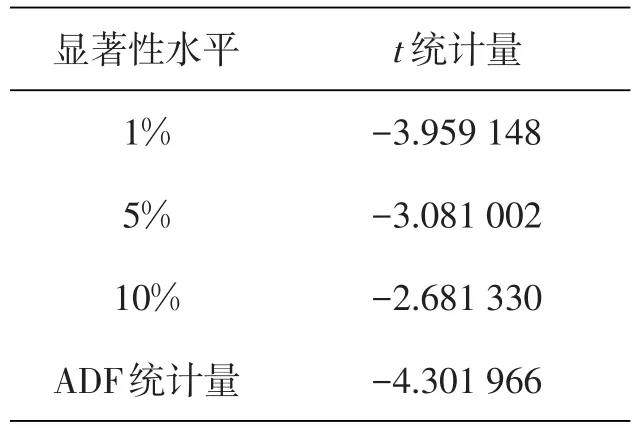
表1 dInRGDP的平稳性检验

2.1 ARIMA预测模型

2.1.1 人均GDP平稳性检验

为了消除异方差性，将人均GDP进行对数化处理，记为InRGDP.根据图1InRGDP趋势图，可以看出InRGDP具有明显的上升趋势，说明此序列为非平稳序列，我们要对该序列进行一阶差分使其平稳，从而得到dInRGDP.对dInRGDP做单位根检验，如表1所示，dInRGDP序列的ADF检验的t值小于1%显著性水平的临界值，因此我们可以认为序列dInRGDP平稳.

2.1.2 模型的建立与检验

图2为dInRGDP的自相关和偏相关图，通过自相关和偏相关图可以看出滞后阶数为1、2和4时自相关系数及偏自相关系数均显著不为零，因此可取p=1,p=2,p=4及q=1,q=2,q=4，为进一步确定模型中的参数p,q，经过多次尝试建立多个模型通过AIC、HQ和SC准则定理进行判断，及通过变量个数较少的原则，综合考虑模型的整体效果，我们将模型确定为ARIMA（1，1，1），具体的表达形式为：

在检验模型是否合理时，我们还需判断残差是否为白噪声序列，如果残差不是白噪声序列，说明模型信息没有利用完全，可以对模型进行改进.当残差为白噪声序列时，认为该模型通过检验.根据图3给出的残差的自相关和偏相关图，根据文献［7］知道最右侧的Prob列的数字表示相应自由度条件下χ2统计量取值大于相应Q值的概率.从图3可知最右侧的Prob列概率值都大于0.05，这说明所有Q值都小于检验水平为0.05的χ2分布临界值（位于临界值左侧），说明残差为白噪声序列，模型通过检验.

利用ARIMA（1，1，1）模型对2010—2014年江苏人均GDP的预测结果如表2所示.

2.2 指数平滑模型预测模型

指数平滑法作为一种时间序列的预测方法，具有预测准确，方法简单等优点，尤其对于那些不存在明显变化趋势的序列预测效果良好.对于变化趋势明显的序列，我们采用二次指数平滑法对其预测，效果会更好.所谓的二次指数平滑法就是在一次指数平滑再进行一次平滑.

图2 dInRGDP的自相关和偏相关图

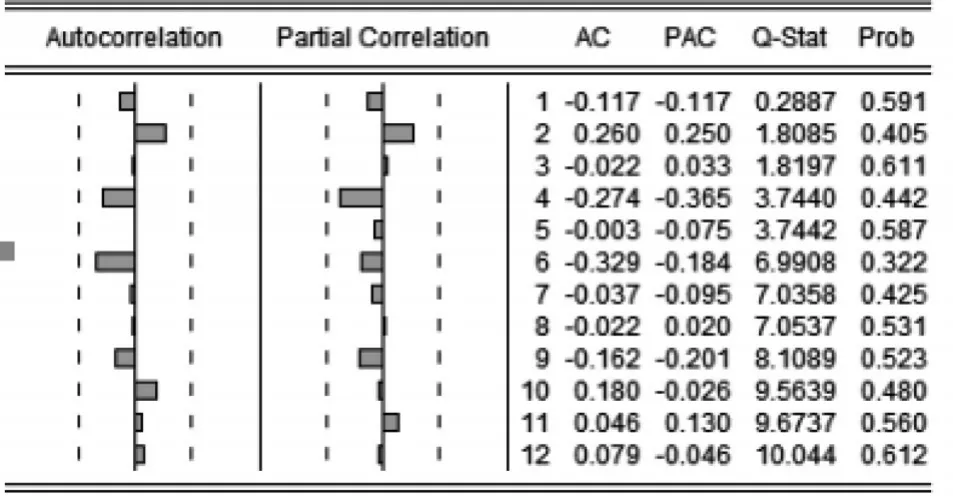
图3 残差序列自相关、偏自相关图

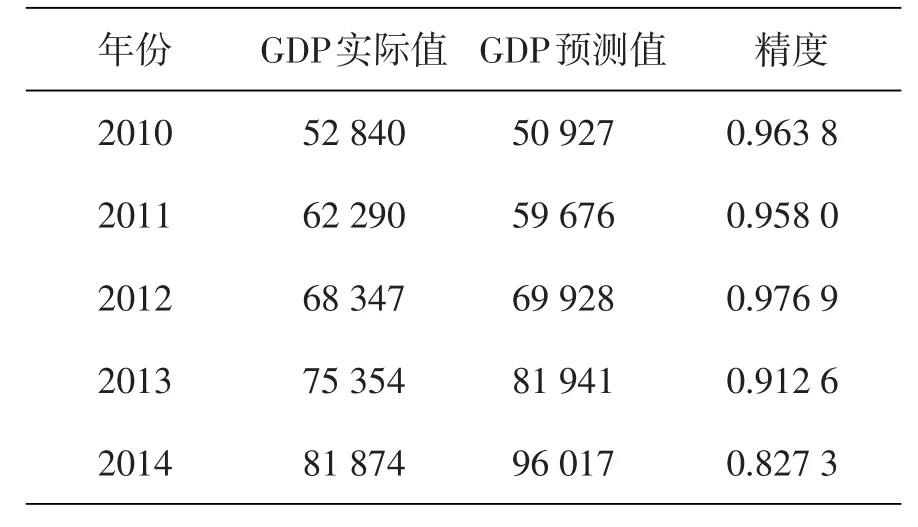
表2 ARIMA（1，1，1）预测结果

根据图1我们可以看出江苏省人均GDP增长趋势明显，我们采用二次指数平滑法预测江苏省人均GDP.

一次指数平滑预测方程形式：

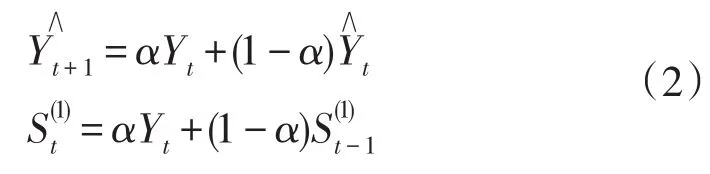
二次指数平滑预测方程的形式为：

表3 指数平滑法预测结果

2.3 多元线性回归预测模型

多元回归模型是用多个解释变量来预测某一变量的预测方法.我们知道财政支出可以刺激GDP的增长，随着财政支出的逐年增加，国内生产总值呈现不断增长的态势，其原因是财政支出拉动了内需，带动了GDP的增长，根据文献［8］，可知财政支出与人均GDP有较为明显的线性关系，因此财政支出可以作为影响人均GDP的解释变量.另外我们知道第三产业在国民经济中始终占有举足轻重的地位，它不仅影响人民的生活还带动了其他产业的发展，进而影响GDP和人均GDP.根据文献［9］，可知人均GDP与第三产业就业人数有一定的联动关系，因而可以把第三产业就业人数作为影响人均GDP的又一解释变量.为了进一步确定第三产业就业人数（x1）、财政支出（x2）作为人均GDP的解释变量，我们进行以下协整检验.

首先对第三产业（x1）和人均GDP做协整检验.

第一步，用OLS法估计协整回归方程得到方程：

第二步，检查残差序列的单整性，看看残差ε序列是否为平稳序列.我们对残差进行单位根检验，其结

果如表4所示.

表4 ε的ADF单位根检验

由表4可知，回归方程的残差是平稳序列，所以我们认为第三产业与人均GDP存在协整关系.

其次，对财政支出（x2）和人均GDP做协整检验.

第一步，用OLS法估计协整回归方程得到方程：

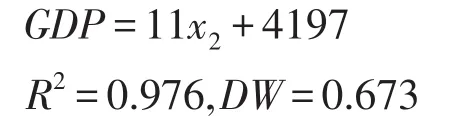
表5 ε的ADF单位根检验

第二步，检查残差序列的单整性，看看残差ε序列是否为平稳序列.我们对残差进行单位根检验，其结果如表5所示.

由表5可知，回归方程的残差是平稳序列，所以我们认为财政支出与人均GDP存在协整关系.

根据上述的协整检验，以江苏省人均GDP（RGDP）为被解释变量，选取江苏省第三产业就业人数（x1）和财政支出（x2）为解释变量建立回归模型，模型结果如下：

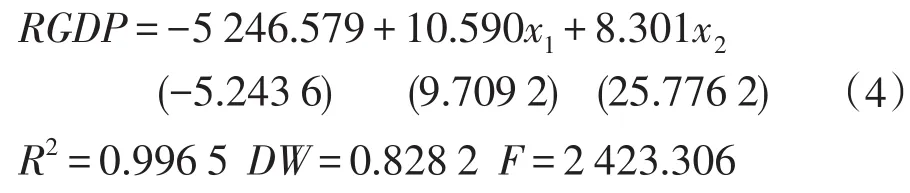
从模型回归结果看出各项系数均通过显著性检验，R2值很大说明模型拟合效果好，用该模型预测江苏人均GDP的结果如表6所示.

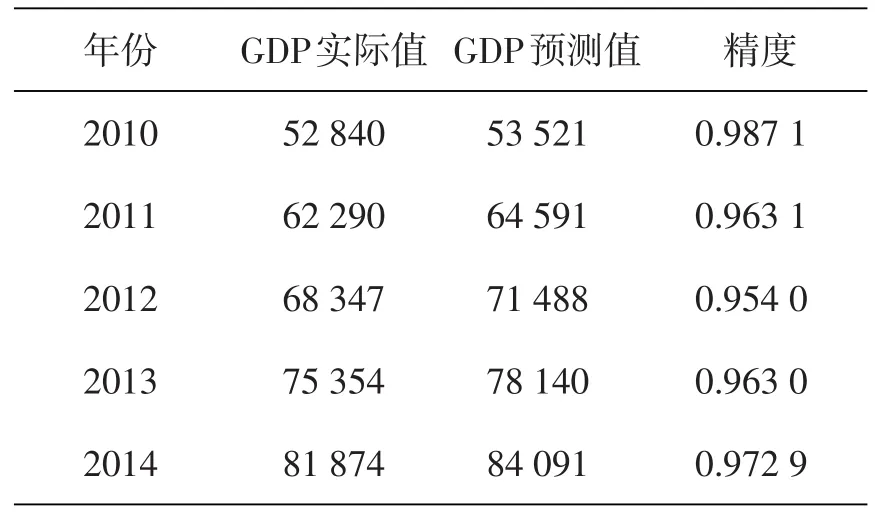
表6 多元线性回归模型预测结果

3 基于IOWGA算子的江苏省人均GDP组合预测模型

3.1 IOWGA算子概念

定义1［10-11］：设为n元函数，设是与OW相关的加权向量，满足：令，公式中的bi表示x1,x2,…,xn按大小顺序排列的第i大的数，我们称fW为n维有序加权几何平均算子，记为OWGA算子.

通过定义1，我们可以知道OWGA算子是先对n个数按从小到大顺序排列之后进行的有序加权几何平均，权系数wi与xi无关，它是与x1,x2,…,xn按大小排列的第i大的数bi有关.

定义2［10-11］：设m个二维数向量

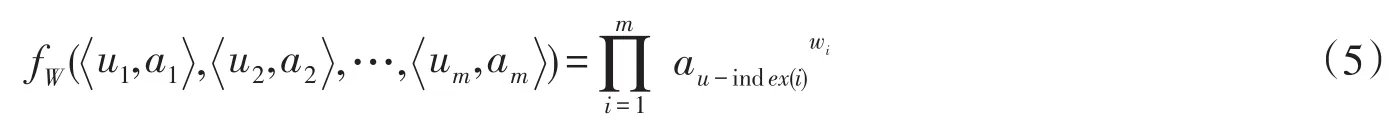
fW称为由u1,u2,…,um所产生的m维诱导有序加权几何平均算子，记为IOWGA算子.其中，ui称为ai的诱导值中按从大到小顺序排列的第i个大的数的下标.是OWGA加权向量，满足

从定义2，我们可以知道IOWGA算子是对诱导值u1,u2,…,um按从大到小顺序排列所对应的a1,a2,…,an中的数进行有序加权几何平均，wi与ai的大小位置无关，而是与诱导值所在的位置有关.

3.2组合预测模型的建立

设某一指标观察值序列为xt,t=1,2,…,N，假设有m个单项预测方法对该序列进行预测；第i种单项预测方法第t时刻的预测值记为xit,t=1,2,…,N,i=1,2,…m；w1,w2,…,wm为m种单项预测方法在组合预测中的加权系数

本文我们把预测精度uit∈[0,1]作为预测值的诱导值，预测精度我们用如下公式表示［12-14］：

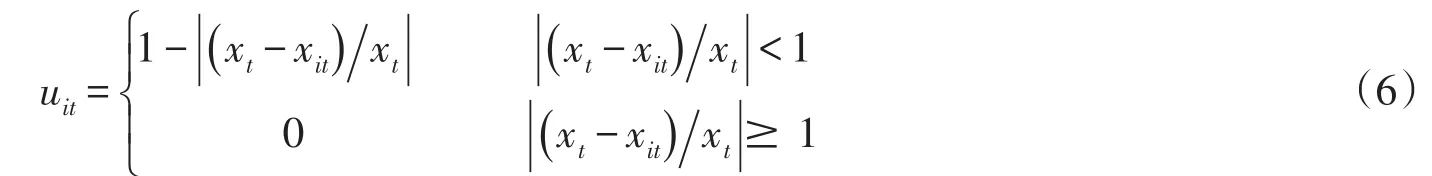
其中uit表示第i种方法在t时刻的预测精度，即为xit的诱导值.这m种单项预测方法在t时刻的预测精度与其对应的预测值就组成m个二维向量为各种单项预测方法在组合预测中的OWGA的加权向量，我们按照从大到小的顺序对m种单项预测方法在t时刻的预测精度序列u1t,u2t,…,umt进行排列，u-index(it)表示第i大的预测精度的下标.我们令：

（6）式为u1t,u2t,…,umt在t时刻所产生的IOWGA组合预测值.该算子考虑到单项预测方法在各时刻差异，组合预测的权重与各个单项预测方法在各个时刻的预测精度大小有关.

为了求解方便，我们将对数误差平方作为优化准则.令eu-index(it)=Inxt-Inxu-index(it)，则前N期的对数预测误差平方和S可以表示为：

在对数误差平方和最小准则下，基于IOGWA算子组合预测模型形式如下：

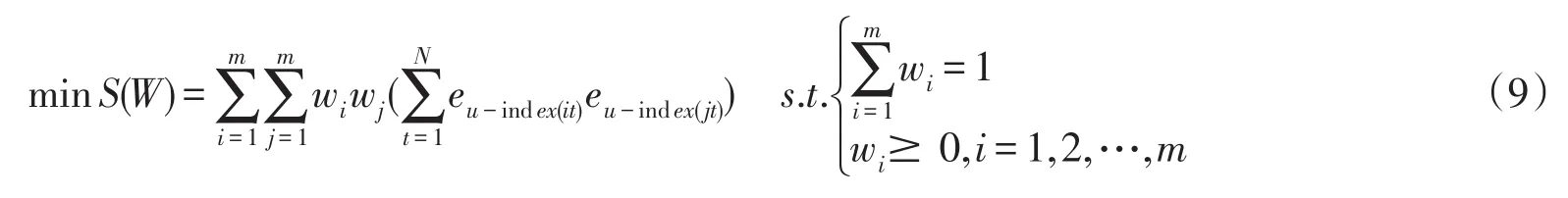
基于（8）式的组合预测模型，将上文的3种单项预测方法ARIMA、指数平滑、多元线性回归用IOWGA算子建立组合预测模型.利用lingo11解（9）得到最优权向量为W=（0.8727，0.1273，0）.因此用组合预测方法对t时刻江苏省人均GDP的预测值可以表示为

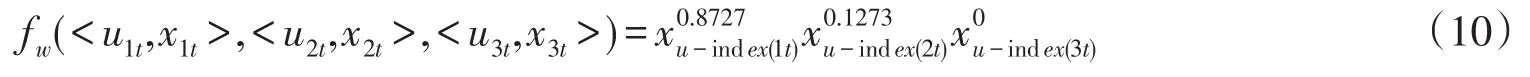
根据模型我们对2010—2014年江苏省人均GDP的预测结果和精度如表7所示.

对比表2、表3、表4、表5的预测结果和精度，我们发现组合预测模型预测结果明显优于其他3种单项预测结果.

3.3 模型的评价

为了体现组合模型比单项预测方法更加有效、精确，在建立组合预测模型时我们还要选取一定指标对模型进行评价.对组合预测评价我们选取如下指标：

表7 组合预测模型模型预测结果

表6给出了单项预测方法和组合预测方法这5个误差评价指标的对比，由表8结果可以看出比起3种单项预测方法的结果，基于IOWGA算子组合预测的结果更加贴近于真实值.

3.4 江苏省人均GDP的预测

利用1990—2014年江苏人均GDP、江苏省第三产业人数、江苏省财政支出等数据，运用上述建立的IOWGA算子的组合预测模型，对2015—2017年江苏省人均GDP进行预测.因为2015—2017年江苏省人均GDP的真实值未知，我们无法知道单项预测方法的预测精度，也就没法利用精度诱导值计算出最优权系数.要想利用上述组合预测模型预计未来的预测值，需要对单项预测方法在未来年份的预测精度做近似估计.根据文献［15］，对于未来第l年的预测精度可以用第i种方法在最近l年的拟合平均精度表示，拟合平均精度公式为

其中，ui(l)表示第i种方法在第N+l的预测精度，uit表示第i种方法在t时刻的预测精度，N表示未来预测的起点（样本数据总量），明显可知，本文N=25.由公式（9）可以计算出2015年ARIMA，指数平滑，多元回归的预算精度分别为0.827 3，0.840 8，0.972 7，因此按照它们预算精度从大到小排名顺序，确定它们在组合预测中的权系数分别为0，0.127 3，0.872 7.同理可以确定2016年ARIMA，指数平滑，多元回归单项预测方法在组合预测中的权系数分别为0.127 3，0，0.872 7；2017年ARIMA，指数平滑，多元回归单项预测方法在组合预测中的权系数分别为0.127 3，0，0.872 7.

对于未来江苏省人均GDP的预测，先利用1990—2014年江苏省人均GDP数据根据ARIMA模型及指数平滑模型给出2015—2017年单项预测，对于多元线性回归模型，先对各因素进行预测然后根据式（3）计算2015—2017年的江苏人均GDP.最后根据前面分析确定的2015—2017年3种单项方法的权系数，利用基于IOWGA算子的组合预测模型求出2015—2017年江苏省人均GDP的预测值.其预测结果如表9所示.

表9 2015—2017江苏省人均GDP预测值

根据表7组合的预测结果，可以计算出2015年较前一年的人均GDP增长率为13.8%，2016，2017年的增长率分别为24.1%、17.9%.由此可以看出未来几年内江苏人均GDP依然处于快速增长的状态，这对于江苏省的经济发展，江苏人民生活水平的提高有一定的参考价值.

4 结束语

在有序加权几何平均（IOWGA）算子的组合预测模型的理论基础上，首先分别用ARIMA模型、指数平滑模型和多元回归模型3种单项预测方法对1990—2009江苏人均GDP进行预测，随后用这3种单向预测方法的误差为诱导值建立IOWGA算子的组合预测模型，并建立预测有效评价指标.从结果可以看出，有序加权几何平均（IOWGA）算子的组合预测模型的预测精度明显高于其他3种单向预测方法.说明组合模型克服了单项预测和传统组合预测的缺点，大大提高了预测精度.在此基础上，采用有序加权几何平均（IOWGA）算子的组合预测模型对2015—2017 3年的人均GDP进行预测.从预测结果可以看出未来几年江苏省经济仍将快速发展，人民生活将进一步提高.

［1］陈海波，刘洁.江苏省人均GDP时间序列模型的建立［J］.统计与决策，2002（11）：17.

［2］陈洁，曹克章，刘哲.基于时间序列的江苏人均GDP预测研究［J］.南京工程学院学报（社会科学版）：2015，15（4）：74-78.

［3］周慕鸿.江苏省房地产业与人均GDP的相关性研究：基于SHTO理论的实证分析［J］.现代经济信息，2013（22）：470-471.

［4］王秋萍，刘素兵，张军.基于IOWGA的组合模型在城镇居民收入中的研究［J］.西安工业大学学报，2007，27（5）：495-499.

［5］颜筱红.基于IOWGA算子的能源消费组合预测模型［J］.西南民族大学学报（自然科学版），2011，37（4）：543-547.

［6］莫颂娟，杨桂元，罗阳.基于IOWGA算子的中国GDP总量的组合预测［J］.统计与决策，2015（16）：4-7.

［7］张晓峒.计量经济学软件Eviews使用指南［M］.天津：南开大学出版社，2004.

［8］熊凤平.人均GDP对财政支出的影响模型及分析［J］.北方经济（学术版），2007（1）：88-89.

［9］刘江.中国GDP与第三产业就业的动态关联分析：基于VAR模型［J］.中国集体经济，2008（4）：4-6.

［10］陈华友，盛昭瀚.一类基于IOWGA算子的组合预测新方法［J］.管理工程学报，2005，19（4）：36-39.

［11］莫颂娟，杨桂元，罗阳.基于IOWGA算子的中国GDP总量的组合预测［J］.统计与决策，2015（16）：4-7.

［12］吴青青，杨桂元.基于IOWGA算子的我国第三产业GDP的组合预测［J］.统计与决策，2015（19）：68-71.

［13］王彬.基于IOWGA算子的组合预测方法及其应用［J］.西安工程大学学报，2012，26（1）：108-111.

［14］陈启明，陈华友.基于IOWGA算子的最优组合预测模型及应用［J］.统计与决策，2012（3）：88-91.

［15］吴凤平，曹艳国.基于IOWA算子的港口吞吐量组合预测方法［J］.经济，2013，9（5）：11-14.

Combination Forecasting Model of GDP Per Capital of Jiangsu Province Based on IOWGA Operator

TU Yang,YANG Guiyuan
(Institute of Quantitative Economics,Anhui University of Finance and Economics,Bengbu 233000,China)

By using the sample data of GDP per capital from 1990 to 2009 and the verification data of GDP per capital from 2010 to 2014 in Jiangsu province respectively,the authors of this paper established three single forecasting models with ARIMA model,multiple regression and exponential smoothing to predict GDP per capital in the next three years in Jiangsu province.Then the paper purposed the concept of induced ordered weighted geometric averaging(IOWGA)operators,established the new combination forecasting model,and made the appropriate evaluation on the basis of three kinds of the single forecasting model.Finally,GDP per capital in Jiangsu province in the next three years was predicted in the paper by the above combination forecasting model.The results show that the combination forecasting model is more accurate and effective.The forecasting results of combination forecasting model show that per capital GDP will be grown rapidly,and that people's living standards will be further improved in the next three years.

IOWGA operator;combination forecasting;GDP per capital

F224.0

A

1008-2794（2017）02-0078-07

2016-03-24

国家社科基金项目“组合预测模型与方法创新及其优化理论研究”（12BTJ008）

涂洋，硕士研究生，研究方向：微分动力系统、经济系统动态分析，E-mail：18895689136@163.com.