超高性能混凝土单轴受压本构关系
2017-04-11郭晓宇亢景付朱劲松
郭晓宇 亢景付,2 朱劲松,2
(1天津大学建筑工程学院, 天津 300072)(2天津大学滨海土木工程结构与安全教育部重点实验室, 天津 300072)
超高性能混凝土单轴受压本构关系
郭晓宇1亢景付1,2朱劲松1,2
(1天津大学建筑工程学院, 天津 300072)(2天津大学滨海土木工程结构与安全教育部重点实验室, 天津 300072)
为研究超高性能混凝土的单轴受压本构关系,分析比较了不同文献提出的超高性能混凝土单轴受压本构方程的异同,建议了统一的超高性能混凝土单轴受压本构方程形式.基于超高性能混凝土单轴受压试验数据,拟合得到计算峰值压应变和弹性模量的经验公式,并提出了超高性能混凝土单轴受压应力-应变曲线上升段参数的计算公式.结果表明:采用《混凝土结构设计规范》(GB 50010—2010)中提供的本构方程形式计算超高性能混凝土的单轴受压应力-应变关系是可行的;轴心抗压强度在80~150 MPa范围内,当轴心抗压强度相同时,圆柱体试件对应的峰值压应变较棱柱体高5.0×10-4~7.5×10-4,且轴心抗压强度越高两者差异越大;所提的峰值压应变、弹性模量计算公式和应力-应变曲线上升段参数计算公式具有较高的准确性和可靠性,可用于超高性能混凝土结构的工程设计.
超高性能混凝土;单轴受压;本构方程;峰值应变;弹性模量;应力-应变曲线上升段参数
超高性能混凝土(ultrahigh performance concrete,UHPC)是一种集超高强度、超高韧性、高耐久性、抗高温、抗冲击等多重优势于一体的新型水泥基复合材料,正逐步应用于高层建筑、大跨桥梁等工程建设领域.活性粉末混凝土(reactive powder concrete,RPC)是国内外应用最广的一种超高性能混凝土,制约其在结构工程中应用的主要因素之一是本构关系不确定.目前,国内外对活性粉末混凝土本构模型的研究还很不成熟,试验研究获得的数据有限、离散性较大,尚未获得公认的单轴本构关系模型.因此,有必要对活性粉末混凝土的本构模型进行深入分析,以期形成有共识的单轴应力-应变关系.
本文首先对国内外文献中提出的超高性能混凝土单轴受压应力-应变全曲线方程进行总结,对比分析不同本构方程的特点和适用性,在此基础上建议了合理统一的超高性能混凝土单轴受压本构方程.然后,基于搜集到的国内外试验数据,分别对超高性能混凝土立方体抗压强度、峰值压应变和弹性模量与轴心抗压强度的关系进行拟合,提出了相应的经验计算公式.最后,提出了单轴受压应力-应变曲线上升段参数的计算公式.
1 应力-应变全曲线方程
对于普通混凝土,研究人员为准确拟合其单轴受压应力-应变曲线,提出了多种数学函数形式的曲线方程,如多项式、指数式、三角函数和有理分式等.对于曲线的上升段和下降段,可采用统一方程,也可采用分段公式[1].对于超高性能混凝土,法国土木工程学会通过大量研究,于2002年制订了超高性能纤维增强混凝土临时指南[2];日本土木工程协会也于2004年制订了相应的设计施工指南[3].两国指南均采用直线来定义超高性能混凝土单轴受压应力-应变曲线的上升段,即应力随应变增加而线性增加.同时,国内外学者在对超高性能混凝土进行轴压试验的基础上,建立了多种形式的超高性能混凝土单轴受压本构方程[4-17].本节按应力-应变曲线上升段方程的函数形式分类,并进行归纳总结.文中提到的超高性能混凝土均指活性粉末混凝土.
1.1 多项式
文献[4-6]通过数学推导和理论分析,结合试验数据,拟合出超高性能混凝土单轴受压应力-应变全曲线方程,即
(1)
式中,x=εc/εco,其中,εc为混凝土应变,εco为峰值应变;y=σc/fc,其中,σc为混凝土应力,fc为棱柱体轴心抗压强度;A=Ecεco/fc为上升段参数,即初始弹性模量与峰值割线模量的比值,其中,Ec为弹性模量;B为下降段参数.需要指出的是,文献[4-5]中掺加纤维为钢纤维,文献[6]中掺加纤维为玄武岩纤维.
文献[7-9]通过力学试验和数学分析,给出了超高性能混凝土的单轴受压本构方程,即
(2)
其中,文献[7]中上升段参数的最佳取值范围为1.1≤A≤1.4,下降段参数的最佳取值范围为6.0≤B≤10.0.
文献[10]通过对比不同水胶比和钢纤维体积掺量下活性粉末混凝土的轴压应力-应变全曲线,提出了不同配合比情况下活性粉末混凝土单轴受压应力-应变全曲线的数学表达式,即
(3)
式中
a1=-6.25λ2+4.12λ+0.42
a2=0.148λ2+0.102λ+0.048
α=2.42λ2+2.26λ+2.60
β=-3.37λ2-3.36λ-3.73
式中,λ为水胶比.式(3)的适用范围为:水胶比λ∈[0.20,0.24],钢纤维体积掺量Vs∈[1%,3%].
文献[11]通过拟合试验曲线,得到活性粉末混凝土单轴受压应力-应变全曲线方程为
(4)
式中
1.2 有理分式
文献[12-14]建立的超高性能混凝土单轴受压本构方程为
(5)
其中,文献[12-13]中掺加纤维为钢纤维,文献[14]中掺加纤维为玄武岩纤维.
文献[15]基于试验结果,对不同配合比的活性粉末混凝土单轴受压应力-应变全曲线进行回归分析,将曲线上升段和下降段统一用一个非线性方程式表示,即
(6)

1.3 指数函数
文献[16]提出了不同养护条件下超高性能混凝土单轴受压应力-应变曲线上升段的曲线方程为
(7)
式中,p为线性折减系数,即真实应力与理想线弹性曲线上对应应力的差值.在蒸压养护条件下,a=0.001,b=0.24.
文献[17]通过拟合试验实测的超高性能混凝土单轴受压应力-应变曲线,得到上升段曲线方程为
0≤εc≤εco
(8)
在对超高性能混凝土受压应力-应变试验曲线进行拟合时,文献[4-14]采用的典型无量纲化受压应力-应变全曲线的全部几何特征[1]与普通混凝土相同,并且最后建立的本构方程形式也与普通混凝土对应的方程形式类似;文献[15,17]基于最小二乘原理分别采用有理分式和指数式的形式拟合出超高性能混凝土受压应力-应变试验曲线;文献[16]将试验曲线上升段与理想线弹性曲线进行对比,在分析试验曲线上升段线性程度的基础上,按照折减系数的方法得到了受压应力-应变曲线上升段的曲线方程.然而,相比于普通混凝土,对于超高性能混凝土单轴受压本构模型的研究还存在一些不足:① 试验方法不统一,不同学者由试验获得的曲线下降段相差较大.不同研究者为获得稳定的曲线下降段采用的试验方法不尽相同,主要包括采用刚性辅助架增加普通试验机刚度、直接采用电液伺服试验机加载以及在电液伺服试验机上附加刚性元件等方法.② 试验研究获得的数据量较少,离散性较大.③ 不同文献提出的本构方程以及曲线上升段和下降段参数只适用于各自的试验结果,不具有普遍适用性.因此,有必要在确定标准试验方法的基础上进行大量的试验研究,以获得具有普遍适用意义的本构模型.
2 上升段曲线方程
建立超高性能混凝土单轴受压本构模型的关键在于确定合理的曲线方程形式以及上升段和下降段参数.由于单轴受压应力-应变曲线的上升段受试验条件的影响较小,首先对上升段不同形式的曲线方程进行对比分析,以期获得统一形式的上升段曲线方程.将式(6)~(8)进行无量纲化处理后可得
(9)
(10)
(11)
式(10)和(11)的上升段参数A具有相同的物理含义,表示初始弹性模量与峰值割线模量的比值,但取值范围存在差异.
《混凝土结构设计规范》(GB 50010—2010)[18]给出了C20~C80混凝土单轴受压本构方程,将其进行无量纲化处理后可得
(12)
将文献[4-5,7-17,19]中基于试验数据得到的上升段参数代入式(12),并与文献中提出的曲线方程进行比较,绘出各自的单轴受压应力-应变曲线上升段,结果见图1.由于文献[15]中本构方程式的参数不具有明确的物理含义,故图1(f)中对应的A值采用文献试验数据按公式A=Ecεco/fc计算求得,并取平均值.
由图1可知,式(12)计算得到的曲线与式(1)、(3)、(9)、(10)、(11)求得的曲线基本重合,与式(2)和(5)求得的曲线偏差不大,与式(4)在Vs=5%情况下求得的曲线存在一定差异,而与其他较低钢纤维体积掺量时获得的曲线仍基本吻合.已有研究表明,钢纤维体积掺量并不是越多越好,当钢纤维体积掺量超过3%后,超高性能混凝土的抗压强度和弹性模量均会降低,并且在搅拌过程中纤维易发生结团现象,影响施工性能,一般建议2%为钢纤维的最佳体积掺量[20].由此可见,在实际工程应用范围内《混凝土结构设计规范》(GB 50010—2010)[18]中提出的上升段本构方程可用于拟合超高性能混凝土的单轴受压应力-应变曲线上升段,在保证较高准确性和可靠性的情况下,具有较好的普遍适用性.A值越大,无量纲化应力-应变曲线上升段越陡,初始直线段长度越短.

(a) 式(1)和(12)
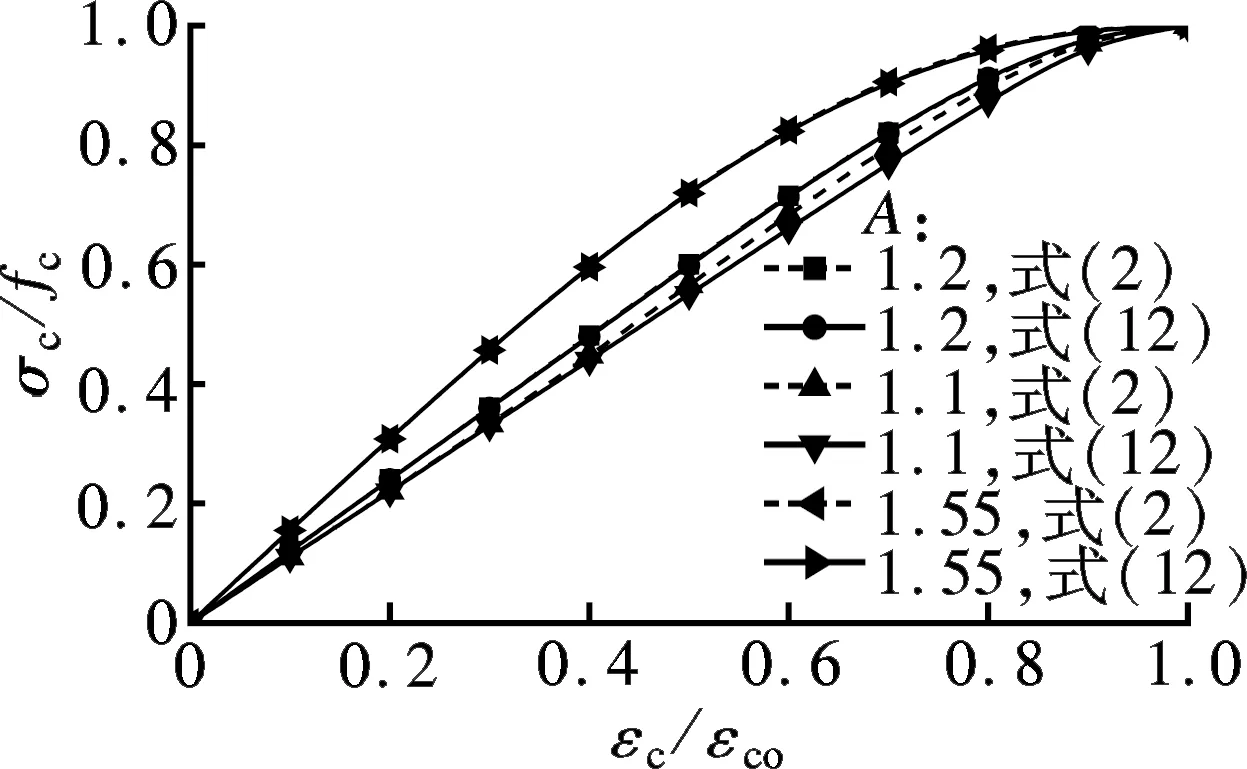
(b) 式(2)和(12)

(c) 式(3)和(12)(A=1.047)
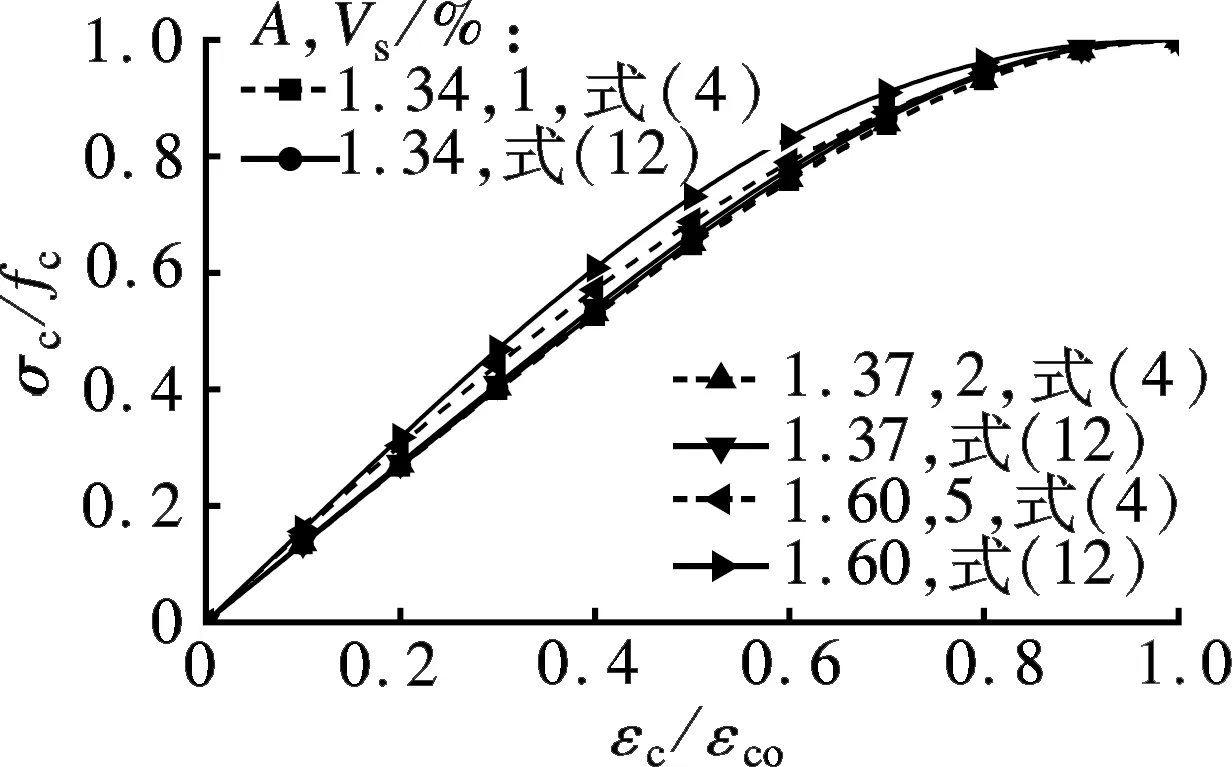
(d) 式(4)和(12)

(e) 式(5)和(12)
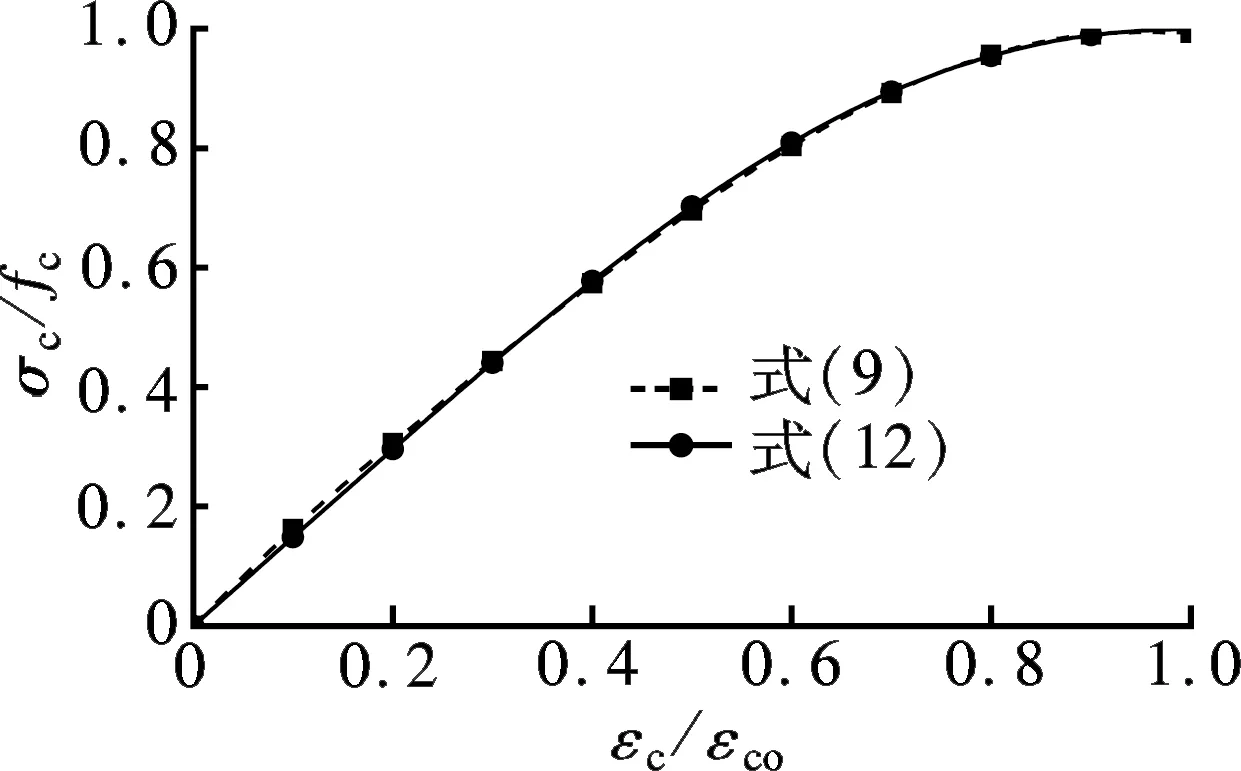
(f) 式(9)和(12)(A=1.486)
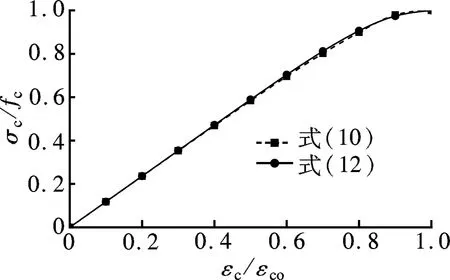
(g) 式(10)和(12)(A=1.18)
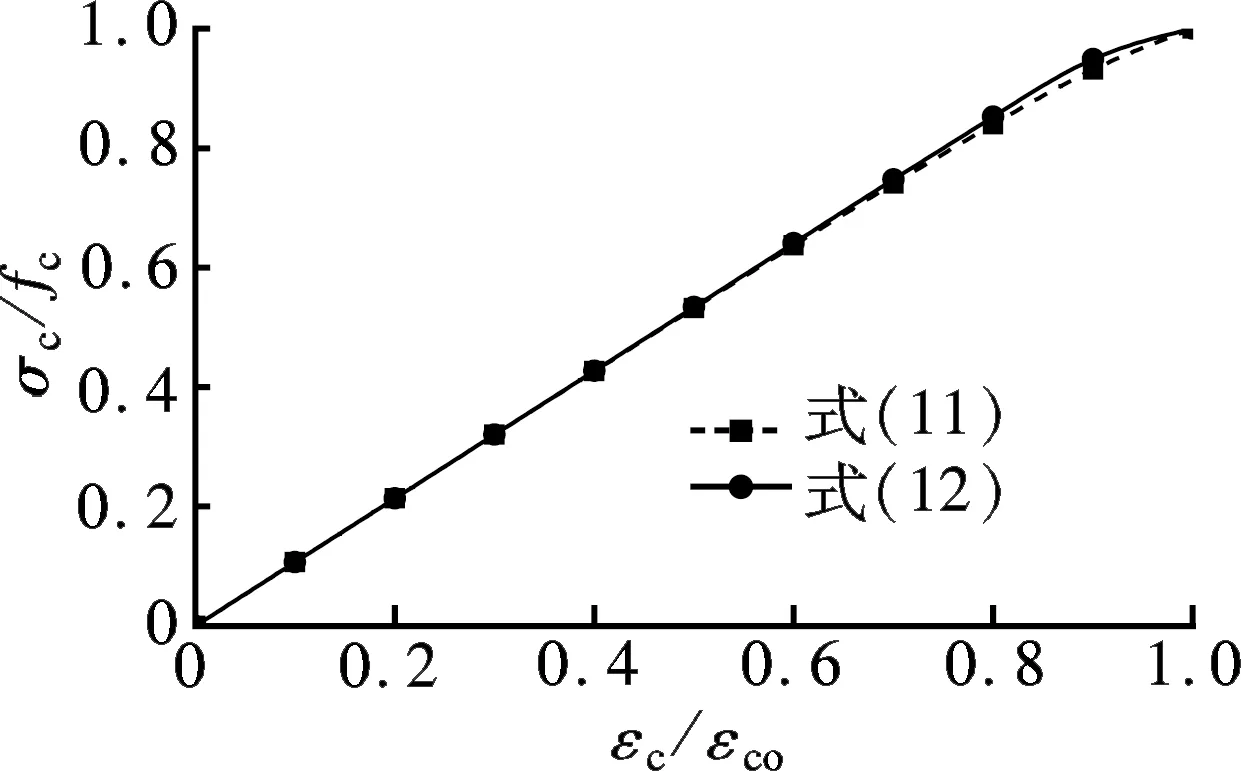
(h) 式(11)和(12)(A=1.068)
3 轴压力学性能指标
3.1 立方体抗压强度与轴心抗压强度
为获得超高性能混凝土立方体抗压强度,国内外学者大多采用边长为100 mm的立方体试件进行试验;为得到轴心抗压强度,试验中采用的试件尺寸存在差异,国内一般采用棱柱体试件,尺寸为100 mm×100 mm×300 mm,而国外一般采用圆柱体试件,其直径为100 mm,高度为200 mm.混凝土的轴心抗压强度一般随立方体抗压强度单调增长,根据文献[6-8,13-15,19,21-22]中的试验数据,图2给出了超高性能混凝土棱柱体轴心抗压强

图2 轴心抗压强度与立方体抗压强度关系

3.2 峰值应变
与普通混凝土类似,超高性能混凝土棱柱体或圆柱体试件达到极限强度时对应的峰值应变虽有较大的离散性,但其随强度单调增长的规律较明显.图3给出了文献[4-10,12-13,17,19,22-25]中59组棱柱体试件试验数据与文献[15-16,26-29]中45组圆柱体试件试验数据的分布情况.基于图3中的试验数据,可得峰值应变εco与棱柱体轴心抗压强度fc之间的关系式为
εco=(6.726 4fc+2 460.9)×10-6
80 MPa≤fc≤150 MPa
(13)

(14)
对于棱柱体试件,由式(13)求得的峰值应变

(a) 棱柱体试件

(b) 圆柱体试件
与实测峰值应变比值的平均值为1.03,均方差为0.015;对于圆柱体试件,由式(14)求得的峰值应变与实测峰值应变比值的平均值为1.00,均方差为0.010.由此可见,式(13)和(14)能够较准确地预测出超高性能混凝土峰值压应变随轴心抗压强度的变化趋势.
由图3可知,相比于棱柱体试件,圆柱体试件对应的峰值应变更大,在80~150 MPa轴心抗压强度范围内,轴心抗压强度相同时圆柱体试件对应的峰值压应变较棱柱体试件高5.0×10-4~7.5×10-4,并且随强度的提高,两者的差异逐渐增大.从搜集到的试验数据来看,目前国外配制的超高性能混凝土强度范围为80~220 MPa,而国内配制的超高性能混凝土强度普遍较低,多为80~150 MPa,应加强150 MPa以上超高性能混凝土的试验研究.
3.3 弹性模量
弹性模量是材料变形性能的主要指标,已有大量试验给出了普通混凝土的弹性模量随强度而单调增长的规律,并且建议了多种弹性模量经验计算公式[1].鉴于测试试件形状和尺寸的差异,图4给出了文献[4-10,12-13,19,21-24]中89组超高性能混凝土棱柱体试件和文献[15-16,26-29]中45组超高性能混凝土圆柱体试件的弹性模量随轴心抗压强度变化的分布情况.若文献中未明确给出试件的弹性模量时,弹性模量取应力为0.5倍轴心抗压强度时对应的割线模量值.参考普通混凝土弹性模量计算公式形式,分别对超高性能混凝土棱柱体和圆柱体试件的试验数据进行拟合.棱柱体的拟合公式为
60 MPa≤fc≤150 MPa
(15)
圆柱体的拟合公式为
(16)
拟合曲线见图4.由图可见,棱柱体和圆柱体试件的弹性模量随轴心抗压强度变化趋势相同,2条拟合曲线基本平行.当轴心抗压强度为80~150 MPa时,由式(15)求得的棱柱体试件的弹性模量要比由式(16)求得的圆柱体试件的弹性模量高2~3 GPa.总体来说,两者差别不大,且当轴心抗压强度为80~150 MPa时圆柱体试件的试验数据点均位于棱柱体试件试验数据点分布范围内.为使试验数据在较广泛的强度范围内保持连续性,不考虑试件形状和尺寸差异对试验结果造成的微小差异,将所有试验数据归于一体进行拟合,拟合曲线见图4,拟合公式为
60 MPa≤fc≤220 MPa
(17)
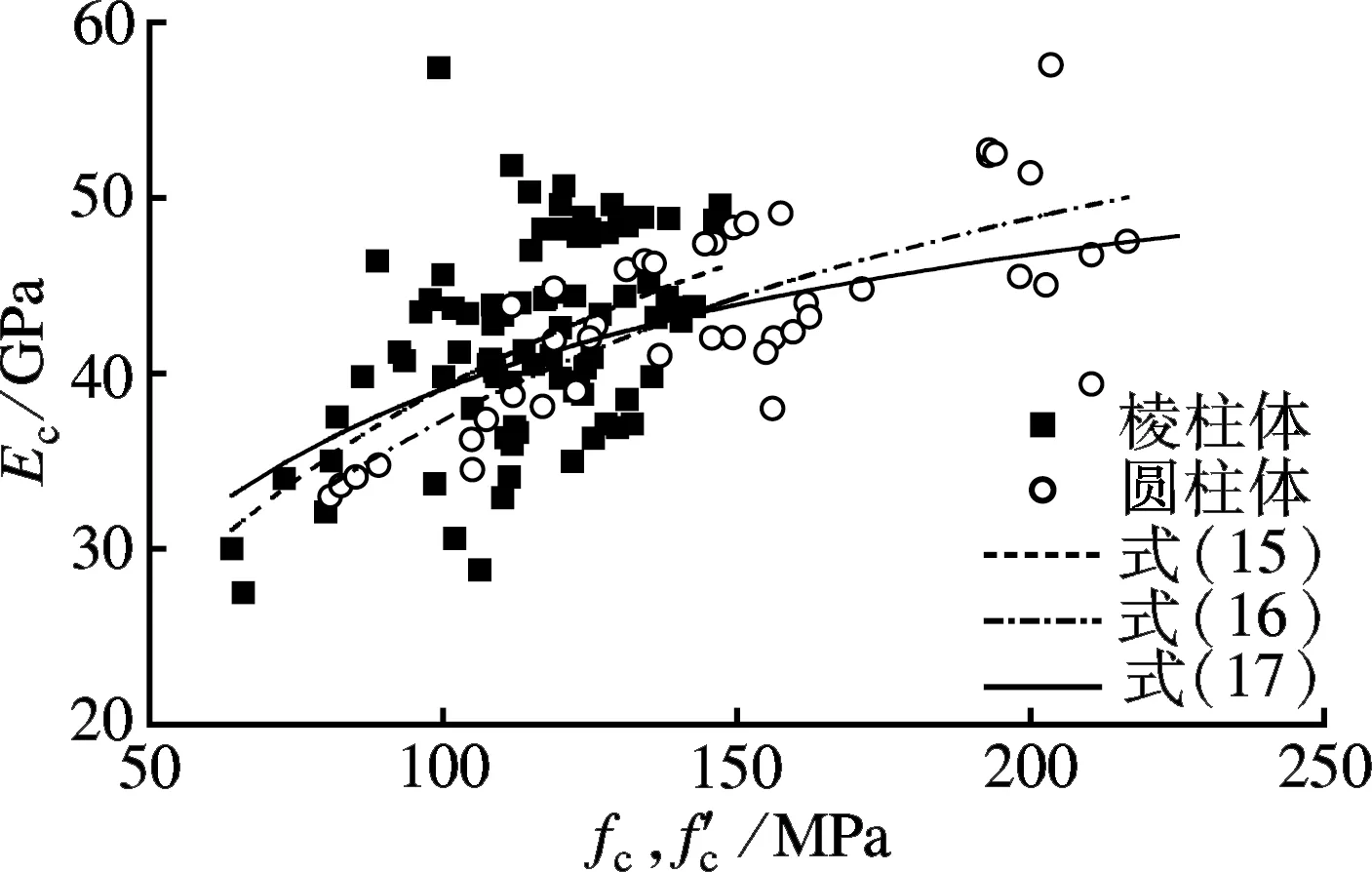
图4 弹性模量与轴心抗压强度的关系
由式(17)计算得到的超高性能混凝土弹性模量与试验实测值比值的平均值为1.00,均方差为0.014.由此可知,当轴心抗压强度为60~220 MPa时,式(17)适用于计算超高性能混凝土的弹性模量,且具有较高的准确性.
4 上升段参数取值
将式(13)、(14)和(17)分别代入式A=Ecεco/fc中,可得超高性能混凝土棱柱体试件单轴受压应力-应变曲线上升段参数A的经验计算公式为
80 MPa≤fc≤150 MPa
(18)
圆柱体试件单轴受压应力-应变曲线上升段参数A的经验计算公式为
(19)
由式(18)求得的棱柱体试件上升段参数与试验实测值比值的平均值为1.01,均方差为0.012;由式(19)求得的圆柱体试件上升段参数与试验实测值比值的平均值为1.00,均方差为0.012.由此可见,将式(18)和(19)用于计算超高性能混凝土圆柱体和棱柱体试件单轴受压应力-应变曲线上升段参数值是可行的,且具有较高可靠性.
图5为超高性能混凝土单轴受压应力-应变曲线上升段参数随轴心抗压强度变化的相关曲线.由图可知,2条曲线走势相同,A值随轴心抗压强度的增大而递减,并逐渐趋近于1,表明超高性能混凝土轴心抗压强度越大,其单轴受压应力-应变曲线弹性段越长.当轴心抗压强度相同时,圆柱体试件的A值更大,说明由圆柱体试件测出的曲线弹性段稍短于棱柱体试件.为了便于对比分析,在图5中同时绘出了由《混凝土结构设计规范》(GB 50010—2010)中公式计算得到的C20~C80(13.4 MPa≤fc≤50.2 MPa)混凝土轴压应力-应变曲线上升段参数随轴心抗压强度的变化曲线.依曲线变化趋势看,超高性能混凝土与C20~C80混凝土基本相同;超高性能混凝土棱柱体试件对应的A值小于C20~C80混凝土,即在峰值应力之前超高性能混凝土单轴受压应力-应变曲线具有更长的弹性段,这与文献[30]中的试验结果一致.
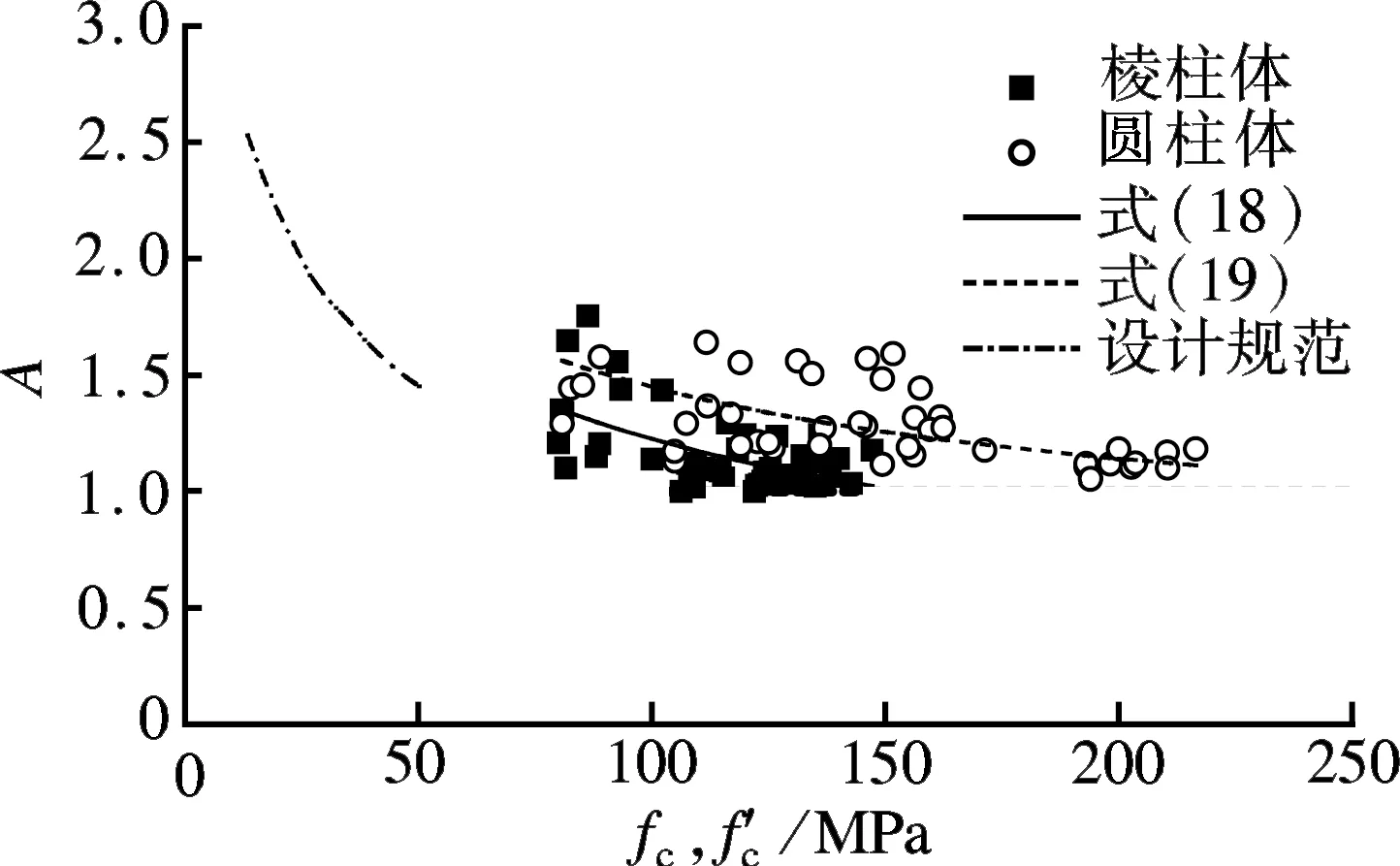
图5 上升段参数与轴心抗压强度的关系
5 下降段曲线方程
由第1节可知,国内外学者对超高性能混凝土单轴受压应力-应变曲线的下降段主要采用有理分式的形式进行拟合,除式(9)外,其他下降段曲线方程式本质上是相同的,且与《混凝土结构设计规范》(GB 50010—2010)中提供的本构方程一致.由式(9)得到的无量纲化轴压应力-应变曲线下降段与设计规范提供的应力-应变曲线下降段(下降段参数B=2.41)的对比情况见图6.由图可知,当1.0≤εc/εco≤1.5时,2条曲线基本重合;当εc/εco>1.5时,2条曲线分离.而文献[15]中由试验获得的应力-应变曲线下降段仅测得了1.0≤εc/εco≤1.5部分,表明设计规范建议的本构方程也可用于拟合文献[15]中的试验曲线.

图6 下降段曲线计算结果与设计规范的比较
综合以上分析,建议采用《混凝土结构设计规范》(GB 50010—2010)中提供的本构方程来拟合超高性能混凝土的单轴受压应力-应变曲线.将文献[4,6-8,12-13,31]中的应力-应变曲线下降段及规范中建议的C80混凝土应力-应变曲线下降段进行无量纲化处理,结果见图7.由图可知,超高性能混凝土单轴受压应力-应变曲线下降段差别较大,对应的下降段参数离散性也较大,暂无明显规律可循,这主要是由于水胶比、纤维种类和体积掺量不同[32]以及试验测试方法的差异造成的,且后者的影响更大.因此,为获得可靠的轴压应力-应变曲线下降段,还需在确定标准试验方法的基础上进行大量的试验研究.

图7 不同文献中下降段曲线对比情况
6 结论
1) 超高性能混凝土单轴受压本构方程大多是基于普通混凝土本构模型的形式建立的,上升段曲线方程多采用多项式、有理分式和指数函数的形式,下降段曲线方程主要采用有理分式的形式.
2) 采用《混凝土结构设计规范》(GB 50010—2010)中提供的本构方程来计算超高性能混凝土单轴受压应力-应变关系是可行的.
3) 建议了超高性能混凝土峰值压应变和弹性模量的经验计算公式,计算值与实测值误差较小,能够较准确地预测出超高性能混凝土峰值压应变和弹性模量随轴心抗压强度单调增加的变化规律.分别提出了超高性能混凝土棱柱体和圆柱体试件单轴受压应力-应变曲线上升段参数的计算公式,计算值与实测值吻合较好,说明公式具有较高准确性和可靠性.
4) 目前国内配制的超高性能混凝土强度普遍较低,主要集中在80~150 MPa,应加强150 MPa以上超高性能混凝土的试验研究.配合比不同以及试验测试方法的差异导致超高性能混凝土单轴受压应力-应变曲线下降段差别较大,对应的下降段参数值离散性也较大,为获得可靠的轴压应力-应变曲线下降段,还需在确定标准试验方法的基础上进行大量的试验研究.
References)
[1]过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003:21-24.
[2]Association Francaise de Genie Civil. Ultra high performance fiber-reinforced concretes-interim recommendations [S]. Paris: Association Francaise de Genie Civil, 2002.
[3]Japan Society of Civil Engineers. Recommendations for design and construction of ultra-high performance fiber-reinforced concrete structures (draft) [S]. Tokyo:Japan Society of Civil Engineers, 2006.
[4]单波.活性粉末混凝土基本力学性能的试验与研究[D].长沙:湖南大学土木工程学院,2002.
[5]吴有明.活性粉末混凝土(RPC)受压应力-应变全曲线研究[D].广州:广州大学土木工程学院,2012.
[6]沈涛.活性粉末混凝土单轴受压本构关系及结构设计参数研究[D].哈尔滨:哈尔滨工业大学土木工程学院,2014.
[7]马亚峰.活性粉末混凝土(RPC200)单轴受压本构关系研究[D].北京:北京交通大学土木建筑工程学院,2006.
[8]安明喆,宋子辉,李宇,等.不同钢纤维含量RPC材料受压力学性能研究[J].中国铁道科学,2009,30(5):34-38. DOI:10.3321/j.issn:1001-4632.2009.05.006. An Mingzhe, Song Zihui, Li Yu, et al. Study on mechanical performance of reactive powder concrete with different steel fiber contents under uniaxial compression [J].ChinaRailwayScience, 2009, 30(5): 34-38. DOI:10.3321/j.issn:1001-4632.2009.05.006. (in Chinese)
[9]Li Li, Zheng Wenzhong, Lu Shanshan. Experimental study on mechanical properties of reactive powder concrete [J].JournalofHarbinInstituteofTechnology(NewSeries), 2010, 17(6): 795-800.
[10]黄政宇,谭彬.活性粉末钢纤维混凝土受压应力-应变全曲线的研究[J].三峡大学学报(自然科学版),2007,29(5):415-420. DOI:10.3969/j.issn.1672-948X.2007.05.008. Huang Zhengyu, Tan Bin. Research on stress-strain curves of reactive powder concrete with steel-fiber under uniaxial compression[J].JournalofChinaThreeGorgesUniversity(NaturalSciences), 2007, 29(5): 415-420. DOI:10.3969/j.issn.1672-948X.2007.05.008.(in Chinese)
[11]鞠彦忠,王德弘,李秋晨,等.钢纤维掺量对活性粉末混凝土力学性能的影响[J].实验力学,2011,26(3):254-260. Ju Yanzhong, Wang Dehong, Li Qiuchen, et al. On the influence of steel fiber volume fraction on mechanical properties of reactive powder concrete[J].JournalofExperimentalMechanics, 2011, 26(3): 254-260.(in Chinese)
[12]闫光杰.200MPa级活性粉末混凝土(RPC200)的破坏准则与本构关系研究[D].北京:北京交通大学土木建筑工程学院,2005.
[13]杨剑,方志.CFRP预应力筋超高性能混凝土T梁的受弯性能[J].铁道学报,2009,31(2):94-103. DOI:10.3969/j.issn.1001-8360.2009.02.018. Yang Jian, Fang Zhi. Flexural behaviors of ultra high performance concrete T beams prestressed with CFRP tendons[J].JournaloftheChinaRailwaySociety, 2009, 31(2): 94-103. DOI:10.3969/j.issn.1001-8360.2009.02.018.(in Chinese)
[14]郑遵畅.玄武岩纤维活性粉末混凝土基本性能试验研究[D].北京:北京交通大学土木建筑工程学院,2012.
[15]Al-Hassani H M, Khalil W I, Danha L S. Proposed model for uniaxial compression behavior of reactive powder concrete [J].JournalofBabylonUniversity(EngineeringSciences), 2015, 23(3): 591-606.
[16]Graybeal B A. Compressive behavior of ultra-high-performance fiber-reinforced concrete [J].ACIMaterialsJournal, 2007, 104(2): 146-152.
[17]徐海宾,邓宗才.新型UHPC应力-应变关系研究[J].混凝土,2015(6):66-68,79. DOI:10.3969/j.issn.1002-3550.2015.06.016. Xu Haibin, Deng Zongcai. Stress-strain constitutive law of a new kind of UHPC [J].Concrete, 2015(6): 66-68,79. DOI:10.3969/j.issn.1002-3550.2015.06.016.(in Chinese)
[18]中华人民共和国住房和城乡建设部.GB 50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
[19]Zhang Z, Shao X D, Li J. Composite bridge deck system with orthotropic steel deck and compact reinforced reactive powder concrete layer [C]//Proceedingof3rdInternationalOrthotropicBridgeConference. Sacramento,CA, USA, 2013: 234-240.
[19]Cao J, Shao X, Zhang Z, et al. Retrofit of an orthotropic steel deck with compact reinforced reactive powder concrete[J].StructureandInfrastructureEngineering, 2015, 58(15): 1-19.
[20]Yoo D Y, Lee J H, Yoon Y S. Effect of fiber content on mechanical and fracture properties of ultra high performance fiber reinforced cementitious composites[J].CompositeStructures, 2013, 106: 742-753. DOI:10.1016/j.compstruct.2013.07.033.
[21]徐海滨.HRB500钢筋预应力超高性能混凝土梁受力性能研究[D].北京:北京工业大学建筑工程学院,2015.
[22]陈红波.配筋超高性能混凝土短梁受剪性能研究[D].长沙:湖南大学土木工程学院,2014.
[23]邓宗才,刘少新,王海忠,等.四种FRP管约束UHPC轴压特性的试验研究[J].北京工业大学学报,2015,41(5):728-734. DOI:10.11936/bjutxb2014090005. Deng Zongcai, Liu Shaoxin, Wang Haizhong, et al. Compressive behavior of four types FRP tube confined ultra-high-performance concrete [J].JournalofBeijingUniversityofTechnology, 2015, 41(5): 728-734. DOI:10.11936/bjutxb2014090005. (in Chinese)
[24]吴香国,郭庆勇,王滨生.超高性能混凝土后张预应力梁抗弯承载力分析[C]//两岸四地高性能与超高性能混凝土学术交流会论文集.北京:中国建材工业出版社,2010:303-310. Wu Xiangguo, Guo Qingyong, Wang Binsheng. Flexure loading capacity analysis of ultra high performance concrete post tension pre-stressing girder [C]//ProceedingsoftheConferenceonHighPerformanceConcreteandUltra-HighPerformanceConcreteinChineseMainland,HongKong,Taiwan,Macao. Beijing: China Building Materials Press, 2010: 303-310. (in Chinese)
[25]吴炎海,何雁斌,杨幼华.活性粉末混凝土(RPC200)的力学性能[J].福州大学学报(自然科学版),2003,31(5):598-602. DOI:10.3969/j.issn.1000-2243.2003.05.021. Wu Yanhai, He Yanbin, Yang Youhua. Investigation on RPC200 mechanical performance [J].JournalofFuzhouUniversity(Natural Science), 2003, 31(5): 598-602. DOI:10.3969/j.issn.1000-2243.2003.05.021. (in Chinese)
[26]Prabha S L, Dattatreya J K, Neelamegam M, et al. Study on stress-strain properties of reactive powder concrete under uniaxial compression [J].InternationalJournalofEngineeringScienceandTechnology, 2010, 2(11): 6408-6416.
[27]Choi H K, Bae B I, Choi C S. Mechanical characteristics of ultra high strength concrete with steel fiber under uniaxial compressive stress [J].JournaloftheKoreaConcreteInstitute, 2015, 27(5): 521-530. DOI:10.4334/jkci.2015.27.5.521.
[28]Graybeal B A. Flexural behavior of an ultrahigh-performance concrete I-girder [J].JournalofBridgeEngineering, 2008, 13(6): 602-610.DOI:10.1061/(asce)1084-0702(2008)13:6(602).
[29]阎培渝.超高性能混凝土(UHPC)的发展与现状[J].混凝土世界,2010(9):36-41. DOI:10.3969/j.issn.1674-7011.2010.09.009. Yan Peiyu. Research and development in UHPC[J].BuildingDecorationMaterialsWorld, 2010(9): 36-41. DOI:10.3969/j.issn.1674-7011.2010.09.009.(in Chinese)
[30]郑文忠,吕雪源.活性粉末混凝土研究进展[J].建筑结构学报,2015,36(10):44-58. DOI:10.14006/j.jzjgxb.2015.10.006. Zheng Wenzhong, Lü Xueyuan. Literature review of reactive powder concrete[J].JournalofBuildingStructures, 2015, 36(10): 44-58. DOI:10.14006/j.jzjgxb.2015.10.006.(in Chinese)
[31]胡楚红.超高性能混凝土叠合梁弯曲性能研究[D].北京:北京交通大学土木建筑工程学院,2013.
[32]张秀芝,孙伟,张倩倩,等.混杂钢纤维增强超高性能水泥基材料力学性能分析[J].东南大学学报(自然科学版),2008,38(1):156-161. DOI:10.3321/j.issn:1001-0505.2008.01.030. Zhang Xiuzhi, Sun Wei, Zhang Qianqian, et al. Mechanical behaviors of hybrid steel fiber reinforced ultra-high performance cementitious composites[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2008, 38(1): 156-161. DOI:10.3321/j.issn:1001-0505.2008.01.030.(in Chinese)
Constitutive relationship of ultrahigh performance concrete under uni-axial compression
Guo Xiaoyu1Kang Jingfu1,2Zhu Jinsong1,2
(1School of Civil Engineering, Tianjin University, Tianjin 300072, China)(2Key Laboratory of Coast Civil Structure Safety of Ministry of Education, Tianjin University, Tianjin 300072, China)
To investigate the constitutive relationship of ultrahigh performance concrete (UHPC) under uni-axial compression, the similarity and the difference of different constitutive equations of UHPC proposed by available literatures are analyzed and compared. The unified constitutive equation of UHPC under uni-axial compression is suggested. The empirical formulas for calculating the peak compressive strain and the elasticity modulus are obtained by fitting the experimental data of UHPC under uni-axial compression. Finally, the calculation formula for the parameters of the stress-strain curve in the ascending phase of UHPC under uni-axial compression is proposed. The research results show that the constitutive equation provided by the Code for Design of Concrete Structures (GB 50010—2010) can be used to calculate the stress-strain relationship of UHPC. When the axial compressive strength is 80 to 150 MPa, the peak compressive strains of the cylinder specimens are 5.0×10-4to 7.5×10-4larger than those of the prism specimens with the same axial compressive strengths. The higher the axial compressive strength is, the larger the difference of the peak compressive strains between the cylinder and the prism specimens. The proposed empirical formulas for the peak compressive strain, the elasticity modulus and the parameter of stress-strain curve in the ascending phase of UHPC have high accuracy and reliability, and can be used for engineering design of UHPC structures.
ultrahigh performance concrete (UHPC); uni-axial compression; constitutive equation; peak strain; elasticity modulus; parameter of stress-strain curve in ascending phase
10.3969/j.issn.1001-0505.2017.02.028
2016-09-02. 作者简介: 郭晓宇(1990—),男,博士生;朱劲松(联系人),男,博士,教授,博士生导师, jszhu@tju.edu.cn.
国家自然科学基金资助项目(51578370)、天津市科技支撑计划重点资助项目(16YFZCSF00460).
郭晓宇,亢景付,朱劲松.超高性能混凝土单轴受压本构关系[J].东南大学学报(自然科学版),2017,47(2):369-376.
10.3969/j.issn.1001-0505.2017.02.028.
TU528
A
1001-0505(2017)02-0369-08
