磁流变阻尼器非参数化模型泛化能力的提高

陈昭晖， 倪一清

(1.福州大学 土木工程学院，福州 350116； 2.香港理工大学 土木及环境工程学系，香港)

磁流变阻尼器非参数化模型泛化能力的提高

陈昭晖1， 倪一清2

(1.福州大学 土木工程学院，福州 350116； 2.香港理工大学 土木及环境工程学系，香港)

建立磁流变阻尼器的动态模型以描述其强非线性动力学行为是智能磁流变控制系统设计及应用的关键环节之一。泛化能力是衡量基于人工神经网络技术的磁流变阻尼器非参数化模型性能的重要指标，也是保证控制系统稳定性和可靠性的重要因素。基于磁流变阻尼器的动力学试验数据，提出贝叶斯推理分析框架下的非线性自回归(non-linear autoregressive with exogenous inputs，NARX)神经网络技术建立磁流变阻尼器的动态模型，通过网络结构优化和正则化学习算法的结合以有效地提高模型的预测精度和泛化能力。研究结果表明，基于贝叶斯推理的NARX网络模型能够准确地预测磁流变阻尼器在周期和随机激励下的非线性动态行为，同时验证了该模型相比于非正则化模型在泛化性能方面的优越性，因此，有利于实现磁流变控制系统的实时、鲁棒智能化控制。

磁流变阻尼器；非参数化模型；NARX神经网络；贝叶斯正则化；泛化能力

智能材料的发展为结构振动控制开辟了新天地，推动着结构控制往智能化方向发展。磁流变液是智能材料研究较为活跃的一个分支，它在磁场作用下可从自由或粘性流动的液体在毫秒级时间范围内转变为具有一定屈服强度的类固体[1]。以磁流变液为工作介质制成的磁流变阻尼器属于半主动控制装置，可通过调节阻尼器内电磁线圈中的电流强度控制磁场强度，从而改变磁流变液的工作状态，实现阻尼力的智能控制。

采用磁流变阻尼器进行结构半主动控制时，为实现高效的控制效果需要在控制系统设计中充分考虑磁流变阻尼器的动力学特性，因此，建立准确、适于实时控制的磁流变阻尼器动力学模型是关键环节之一。但是，磁流变阻尼器的动力学行为由于磁流变液的复杂流变特性而呈现强非线性，增加了阻尼器建模的困难。目前，对于此问题的研究主要采用参数化建模和非参数化建模的方法。参数化模型利用物理元件(如质量、线性/非线性弹簧、线性/非线性阻尼等)和滞回模块(Bingham、Bouc-Wen、Dahl、LuGre等)的串并联组合来模拟阻尼器的力学行为[2-6]。参数化模型通常表达为强非线性方程，虽然在一定范围内能够准确描述磁流变阻尼器的力学行为，但其多参数的优化识别不可避免地受制于初始值、约束条件、收敛性等因素而产生难度。实际控制应用时，对强非线性方程的数值处理可能造成控制滞后，影响控制效果。

非参数化模型主要采用人工神经网络、模糊逻辑、神经模糊推理等技术基于足够丰富的试验数据建立磁流变阻尼器输入、输出的非线性映射关系以表征其动力学行为[7-10]。其中，神经网络具有很强的自学习能力能够获得精确的预测模型。实际应用中，神经网络模型的泛化能力，即网络识别训练数据以外样本的能力，被认为是衡量神经网络性能的重要指标。但以往的研究却很少对磁流变阻尼器的神经网络模型进行泛化能力方面的深入探讨。用于神经网络训练的试验数据不可避免地包含噪声，如果网络结构冗余，这些噪声会影响到整个网络训练后期的收敛，导致训练偏离全局最优点，并造成网络过拟合(overfitting)而记忆了噪声细节，降低泛化能力。过拟合的神经网络模型将无法保障磁流变阻尼器控制系统的稳定性和可靠性。

本文基于磁流变阻尼器的动态性能试验数据，从网络结构和学习算法相结合的角度来研究磁流变阻尼器神经网络模型泛化能力的提高。提出采用NARX模型与神经网络技术相结合的NARX网络建模方法表征磁流变阻尼器的非线性动力学行为，并利用基于贝叶斯推理的学习算法来有效地提高磁流变阻尼器模型在不同输入激励条件下的泛化能力。

1 磁流变阻尼器的动力学试验

以美国LORD公司的RD-8040磁流变阻尼器为试验对象，采用MTS材料试验机进行磁流变阻尼器的动态力学性能测试。试验时，控制MTS作动器输出不同频率和幅值的谐波位移激励信号施加于磁流变阻尼器，同时对阻尼器输入不同的直流电流。图1显示了其中在幅值为5 mm、频率为2.5 Hz的正弦激励以及不同直流输入下的实测位移-阻尼力和速度-阻尼力滞回曲线。由图可见，在无输入电流(0 A)的情况下，磁流变阻尼器的出力由磁流变液的黏性行为及活塞与密封圈间的摩擦主导。随着电流的增大，磁流变阻尼力及耗能能力增大，其增幅随着磁流变液趋于磁饱和状态而减小。当活塞速度较小时，阻尼器呈现出滞回现象，阻尼力随着速度的增加而增大，当速度增大到一定幅值后，阻尼力的增加减缓，阻尼器表现出屈服现象。因此，磁流变阻尼器具有很强的非线性动力特性。

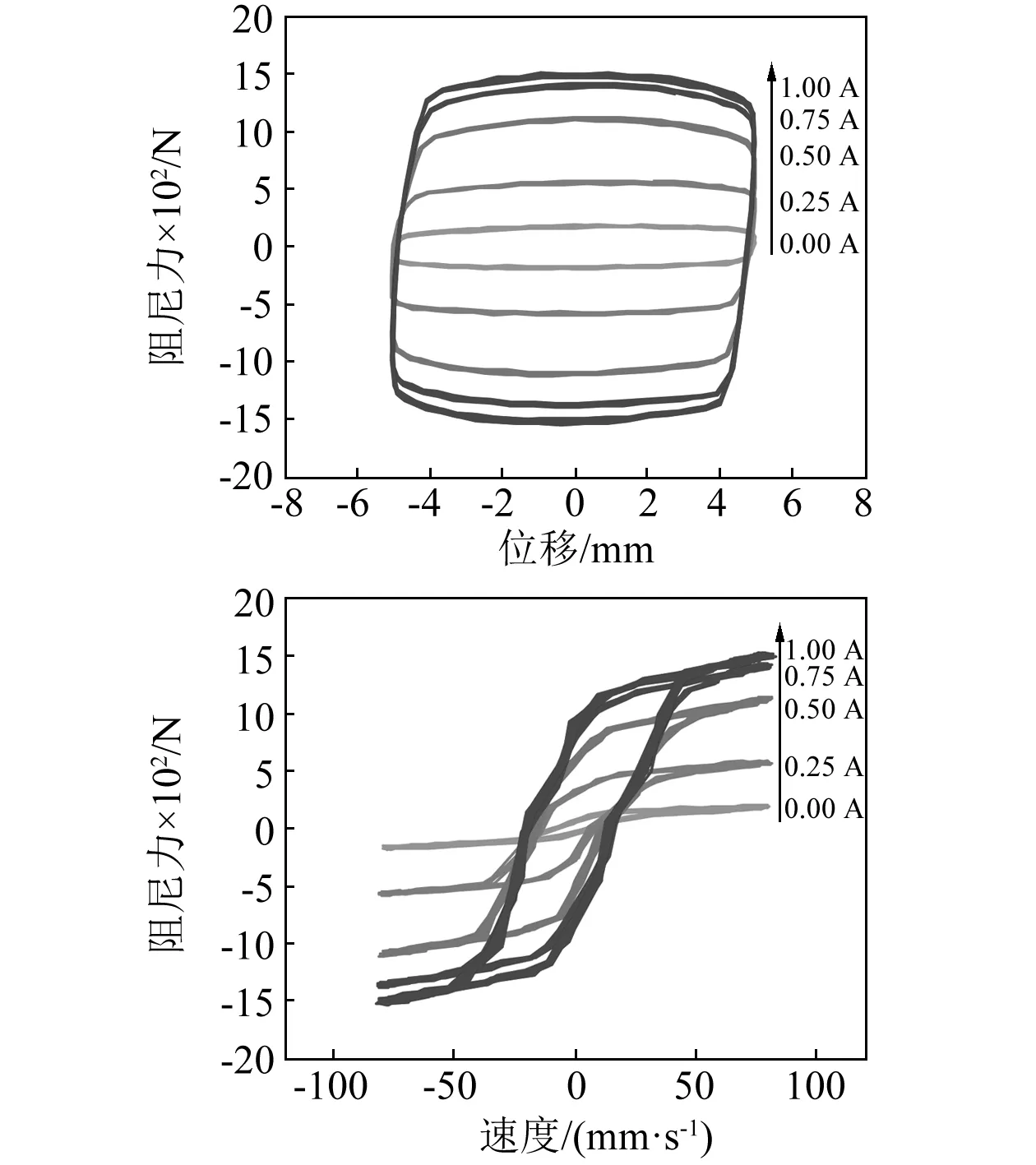
图1 不同电流下的滞回特性曲线(5 mm, 2.5 Hz)Fig.1 Measured hysteresis loops under differentcurrent levels (5 mm, 2.5 Hz)

2 NARX网络建模方法

2.1 NARX网络

NARX模型具有很好的表征非线性动态行为的能力，理论上可以描述任意有限自由度的非线性动态系统[11]。NARX模型用离散时间的输入-输出方程表达为

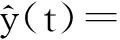
(1)

多层感知器(multilayer perceptron，MLP)是一种前馈神经网络模型，能够反映输入与输出之间的映射关系。它包含多层神经元，各层神经元之间通过连接权以前馈方式传递信息。含有单隐层的MLP已经理论上被证明具有全局逼近能力，即只要其隐层神经元数目足够，通过优化其连接权就能以任意精度逼近非线性连续函数[12]。因此，可以采用MLP网络辨识式(1)的NARX模型f(·;θ)，其参数向量θ则由神经网络参数(连接权和阈值)组成，由此构成的方法为NARX网络，它具有强大的表征复杂非线性行为(如迟滞、饱和、混沌等)的能力[13]。

多输入单输出的NARX网络可表达为

(2)

2.2 贝叶斯学习算法

MLP网络模型的学习训练通常采用最大似然法(如反向传播算法)进行模型参数估计。基于ND个训练数据样本D，通过最小化模型预测值与真实值间的误差平方和指标式(3)确定网络参数

(3)

然而，采用最大似然法训练的MLP网络结构容易过于冗余，导致对训练样本的过拟合现象，即网络模型仅记忆样本数据，而没有学习到数据间的真实映射关系，从而导致网络泛化能力降低，无法对未经训练的输入给出正确的输出预测。

正则化方法是改善网络泛化能力的有效方法之一，其将反应网络结构复杂性的正则惩罚项引入式(3)中改进误差函数形式为

S(θ)=βED+αEθ

2.2.1 网络训练的贝叶斯推理

贝叶斯方法着眼于网络参数在整个权空间中的概率分布，将网络参数视为随机变量。在网络结构确定的情况下，没有样本数据时网络参数的先验分布为P(θ|α)。有了样本数据D后，根据贝叶斯理论，可得网络参数的后验条件概率为

(5)

式中，P(D|θ,β)为似然函数，P(D|α,β)为归一化因子。

假设训练数据D含有零均值高斯噪声，且网络参数θ服从高斯先验分布，则有

P(D|θ,β)=exp(-βED)/ZD(β)

(6)

P(θ|α)=exp(-αEθ)/Zθ(α)

(7)

式中：ZD(β)=(π/β)ND /2，ZD(β)=(π/β)Nθ/2。把式(6)和式(7)代入式(5)可得参数的后验概率分布为

P(θ|D,α,β)=exp(-S(θ))/ZS(α,β)

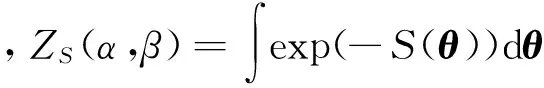
2.2.2 正则化参数的贝叶斯优化

贝叶斯推理学习算法的另一个优势是网络训练过程中可以同步优化正则化参数α和β。根据贝叶斯理论，给定训练数据D后，正则化参数的后验概率为

(9)

假设先验分布P(α,β)满足一种很宽的分布函数，即对α和β不敏感，且归一化因子P(D)与α、β无关，因此，求取正则化参数的最大后验概率分布的问题转化为求解最大似然函数P(D|α,β)。由式(5)～(8)可得，

(10)

当样本数据量较多时，网络参数的后验分布趋于高斯分布，通过简化可求出ZS(α,β)，再将其代入式(10)并取对数后分别对α和β求偏导，可得到

(11a)

(11b)

式中：γeff=Nθ-2αMPtrace((S(θMP))-1)表示实际参与正则化学习的网络参数的数量。由于γeff与α有关，α和β值在网络训练过程中由式(11)进行循环估计。

NARX网络的训练采用具有快速和稳定收敛优势的Levenberg-Marquardt (LM)算法[15]优化网络参数θMP以最小化目标函数(4)。在进行正则化参数优化过程中，需要计算S(θ)在其最小点θMP处的Hessian阵S(θMP)，为减小计算量、提高计算速度，可以利用LM算法对其做近似计算，即

S(θ)MP≈2βMPJTJ+2αMPI

(12)

采用贝叶斯学习算法进行网络训练时，输入和输出数据都归一化为[-1, 1]之间。为避免网络陷入局部最优解，对网络参数随机初始化进行重复训练后取最优。

3 磁流变阻尼器的模型辨识

根据式(1)，磁流变阻尼器的动力学模型可表示为

(13)

(14a)

g2(a)=a

(14b)

式中：隐层激励函数g1(·)赋予NARX网络表征非线性行为的运算能力，这样的网络形式已被证明具有全局逼近能力。式(13)包含了磁流变阻尼器输入输出的多阶时延信息，因此可以反映其动态行为。

基于磁流变阻尼器的性能试验数据，建立其NARX网络模型分为两阶段：①利用训练样本进行网络的贝叶斯学习训练，同时利用验证样本进行网络结构设计；②利用未经训练的测试样本检验优化训练后的网络模型的泛化性能。获取训练、验证和测试数据的实验工况如表1所示，输入激励为各种频率和幅值的谐波位移信号以及不同水平的直流电流。磁流变阻尼器活塞的速度采用有限差分法对位移求导得到。模型的预测性能采用实测阻尼力和模型预测输出之间的均方根(RMS)误差进行评价，即

(15)

表1 NARX网络训练、验证及测试的实测数据样本Tab.1 Measurement data sets for NARX network training, validation and testing

图2 不同输入变量组合下的模型误差分析Fig.2 RMSE analysis for different input combinations(nx=n=nI=0,nF=1,nh=15)

图3 不同输入变量时延阶数下的模型误差分析Fig.3 RMSE analysis for different numbers of input lags

模型输入层结构确定之后，需要进行隐层神经元数目nh的优化选择。图4显示了单隐层NARX网络模型分别设计有5～25个隐层神经元时的训练和验证统计误差。随着nh值的增大，网络参数数量也随之增加，因此，网络具有更强的学习能力，减小了训练误差。但是，过于冗余的网络模型将可能导致过拟合现象。通过贝叶斯正则化对于模型参数大小和数量增长的控制，则可有效地降低验证误差的过度增长。通过权衡图4中训练和验证误差结果，隐层神经元个数选为18。

综上，通过对模型结构和预测精度的比较和权衡，优化后的磁流变阻尼器NARX网络模型具有8个输入神经元、18个隐层神经元和1个输出神经元的结构。

图4 不同隐层神经元数目下的模型误差分析(L=2)Fig. 4 RMSE analysis for different numbers of hidden neurons

4 模型验证

4.1 周期激励下的泛化能力

采用表1的3组周期激励下的测试数据对优化设计的贝叶斯正则化NARX网络模型进行泛化性能检验。表2给出了该模型在测试数据下的预测结果，同时与采用非正则化的普通LM算法得到的NARX网络模型误差进行比较。模型预测误差由式(15)计算得到。由表2可见，贝叶斯NARX网络模型的均方根误差值基本上低于相应的实测阻尼力均方根值(表1)的5%；同时，相比LM算法，采用贝叶斯学习算法可提高模型的预测精度至30%～75%，验证了贝叶斯正则化的NARX网络模型具有很好的泛化能力。由图5可知，贝叶斯NARX网络模型预测的位移-阻尼力和速度-阻尼力滞回曲线与实测结果吻合很好，表明了NARX网络模型对非训练样本的准确预测能力。

4.2 随机激励下的泛化能力

为保证磁流变阻尼器模型在控制应用中的准确预测能力，需获得覆盖磁流变阻尼器工作范围的丰富动态响应信息进行建模。为此，将磁流变阻尼器安装到置于振动台上的钢框架结构上，由振动台产生有限带宽的白噪声基础振动加速度信号，使磁流变阻尼器在随机振动状态下工作，同时对其施加带限白噪声的随机电流，以获取其动态响应。图6显示了在幅值为0.2 g、频率范围为0.8～10 Hz的基础加速度激励以及输入电流幅值为0～2 A、频率范围为0～10 Hz的情况下，磁流变阻尼器的活塞位移、速度、电流和阻尼力时程。利用该组数据分别对上述贝叶斯正则化模型和非正则化模型进行重新学习训练，并采用表3的3组不同输入工况下的测试数据进行泛化性能比较和检验。

表2 周期激励下NARX网络模型泛化能力Tab.2 Generalization performance of NARX networkmodels in harmonic excitation scenarios

图5 周期测试样本3下预测和实测滞回特性曲线的比较Fig.5 Comparison between predicted and measuredhysteresis loops for harmonic testing data set 3

表4比较了随机激励下贝叶斯正则化模型和非正则化模型对测试数据的预测误差。可见，贝叶斯正则化模型对各组测试数据的阻尼力的均方根预测误差均小于相应的实测阻尼力均方根值(表3)的5%。图7显示了贝叶斯正则化NARX网络模型对测试样本3的磁流变阻尼力的预测结果及误差时程，图8比较了相应的预测和实测位移-阻尼力、速度-阻尼力滞回特性曲线，可见模型预测值与测量值吻合很好。此外，与非正则化模型相比，贝叶斯正则化模型的预测误差减小了60%以上，大大提高了磁流变阻尼器模型的泛化能力。

图6 磁流变阻尼器在随机激励下的动态响应Fig.6 Random responses of MR damper

序号输入激励幅值/g频率/Hz输入电流类型幅值/A频率/Hz阻尼力RMS/N10.200.5-10直流1.25-939.420.120.5-10Chirp0-20.1-5671.030.150.5-10随机0-20-10741.3

表4 随机激励下NARX网络模型泛化能力Tab. 4 Generalization performance of NARX network models in random excitation scenarios

图7 随机测试样本3下磁流变阻尼力预测和实测时程的比较Fig.7 Comparison between predicted and measureddamper forces for random testing data set 3

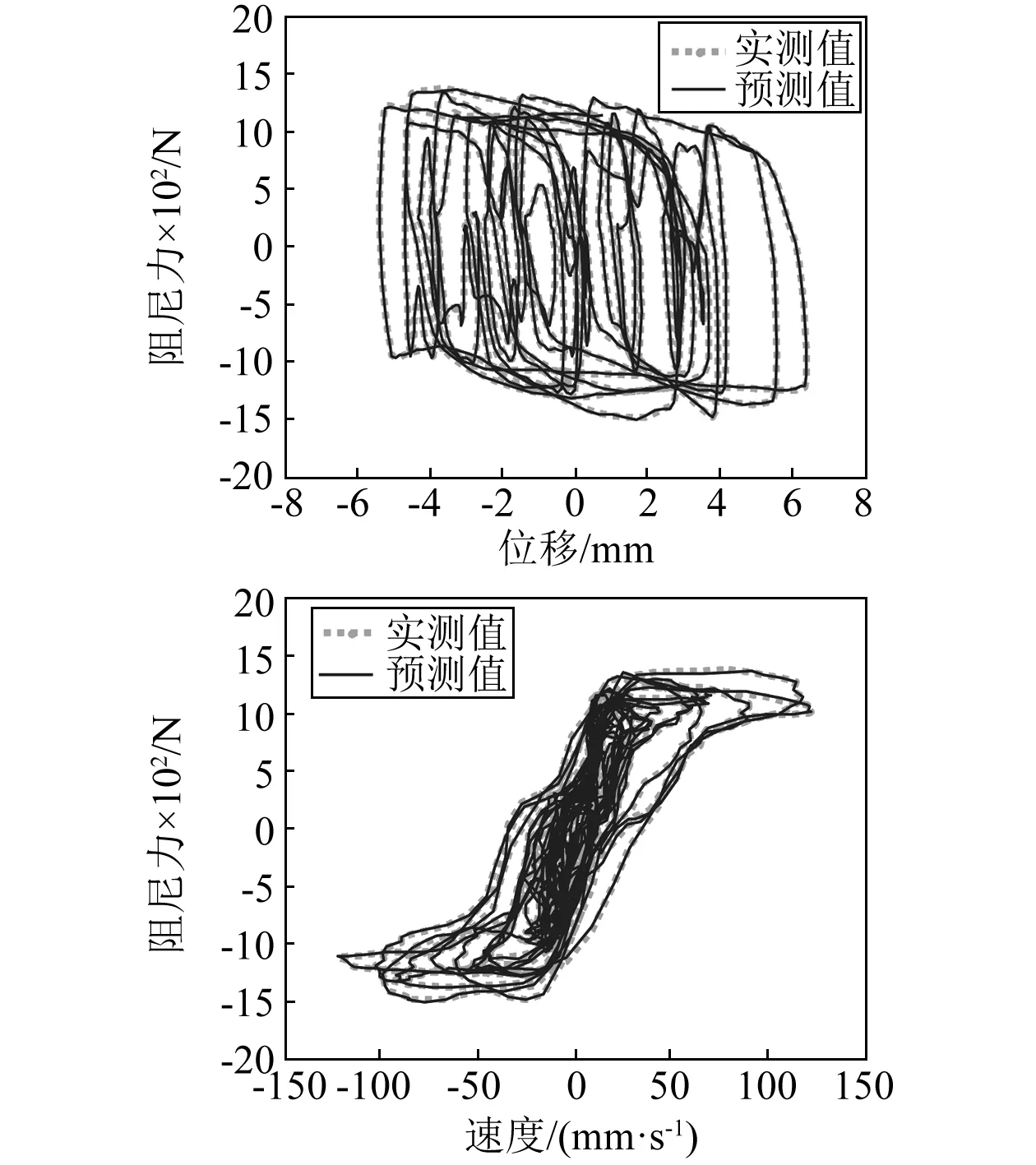
图8 随机测试样本3下预测和实测滞回特性曲线的比较Fig.8 Comparison between predicted and measuredhysteresis loops for random testing data set 3

5 结论

本文利用磁流变阻尼器的动态测试数据，建立基于贝叶斯推理的NARX网络技术的磁流变阻尼器非参数化模型。为保证磁流变阻尼器模型在控制应用中的有效性和可靠性，从网络结构优化和学习算法相结合的角度来提高NARX网络的泛化性能。研究结果表明：

(1)NARX网络结构的合理设计及选取有利于获得结构简单、泛化性能高、计算速度快的动态模型；

(2)基于贝叶斯推理的NARX网络模型能够准确描述磁流变阻尼器在周期激励下的非线性动力学行为，以及准确预测其在随机激励下的阻尼力输出；

(3)由于贝叶斯正则化能有效控制网络的复杂度、减少过拟合，由此得到的NARX网络模型相比非正则化模型具有很好的泛化能力，有利于保持和改善智能磁流变控制系统的有效性、稳定性和鲁棒性。

[ 1 ] CATERINO N, SPIZZUOCO M, OCCHIUZZI A. Promptness and dissipative capacity of MR dampers: experimental investigations [J]. Structural Control and Health Monitoring, 2013, 20(12): 1424-1440.

[ 2 ] SPENCER B F, DYKE S J, SAIN M K, et al. Phenomenological model for magnetorheological dampers [J]. Journal of Engineering Mechanics, 1997, 123(3): 230-238.

[ 4 ] AGUIRRE N, IKHOUANE F, RODELLAR J, et al. Parametric identification of the Dahl model for large scale MR dampers [J]. Structural Control and Health Monitoring, 2011, 19(3): 332-347.

[ 5 ] YANG F, SEDAGHATI R, ESMAILZADEH E. Development of LuGre friction model for large-scale magneto-rheological fluid damper [J]. Journal of Intelligent Material Systems and Structures, 2009, 20(8): 923-937.

[ 6 ] WANG D H, LIAO W H. Magnetorheological fluid dampers: a review of parametric modelling [J]. Smart Materials and Structures, 2011, 20(2): 023001.

[ 7 ] 王修勇, 宋璨, 陈政清, 等. 磁流变阻尼器的性能试验与神经网络建模[J]. 振动与冲击, 2009, 28(4): 42-46. WANG Xiuyong, SONG Can, Chen Zhengqing, et al. Test of a MR damper and its modeling using neural network [J]. Journal of Vibration and Shock, 2009, 28(4): 42-46.

[ 8 ] 王戡, 郑玲, 刘非. 基于广义回归神经网络的磁流变减振器模型辨识[J]. 汽车工程, 2013, 35(7): 619-623. WANG Kan, ZHENG Ling, LIU Fei. Model identification of MR damper based on generalized regression neural network [J]. Automotive Engineering, 2013, 35(7): 619-623.

[ 9 ] ASKARI M, LI J, SAMALI B, et al. Experimental forward and inverse modelling of magnetorheological dampers using an optimal Takagi-Sugeno-Kang fuzzy scheme [J]. Journal of Intelligent Material Systems and Structures, 2016, 27(7): 904-914.

[10] 潘公宇, 杨海, 徐腾跃, 等. 磁流变阻尼器试验与建模研究[J]. 振动与冲击, 2015, 34(6): 36-40. PAN Gongyu, YANG Hai, XU Tengyue, et al. Tests and modeling for magneto-rheological (MR) dampers[J]. Journal of Vibration and Shock, 2015, 34(6): 36-40.

[11] CHEN S, BILLINGS S A, GRANT P M. Non-linear system identification using neural networks [J]. International Journal of Control, 1990, 51(6): 1191-1214.

[12] HORNIK K. Approximation capabilities of multilayer feedforward networks [J]. Neural Networks, 1991, 4(2): 251-257.

[13] SUYKENS J A K, VANDEWALLE J P L, DE MOOR B L R. Artificial neural networks for modeling and control of non-linear systems [M]. Boston: Kluwer Academic, 1996.

[14] MACKAY D J C. A practical Bayesian framework for backprop networks [J]. Neural Computation, 1992, 4(3): 448-472.

[15] HAGAN M T, MENHAJ M B. Training feedforward networks with the Marquardt algorithm [J]. IEEE Transactions on Neural Networks, 1994, 6(5): 989-993.

Enhanced generalization of nonparametric model for magnetorheological dampers

CHEN Zhaohui1, NI Yiqing2

(1. College of Civil Engineering, Fuzhou University, Fuzhou 350116, China；2. Department of Civil and Environmental Engineering, The Hong Kong Polytechnic University, Hong Kong, China)

The dynamic modeling for magnetorheological (MR) dampers to describe their highly nonlinear dynamic characteristics is essential for the design and implementation of a smart MR control system. One critical concern in constructing a nonparametric MR damper model by employing the artificial neural network technique is its generalization capability, which is also significant to guarantee the stability and reliability of the MR control system. The paper presents the modeling of MR dampers with the employment of the NARX (nonlinear autoregressive with exogenous inputs) network technique within a Bayesian inference framework, and addresses the enhancement of model prediction accuracy and generalization capability in terms of the network architecture optimization and regularized network learning algorithm. The Bayesian regularized NARX network model for the MR damper is demonstrated to outperform the non-regularized network model with the superior prediction and generalization performance in the scenarios of harmonic and random excitations. Therefore, the proposed model with enhanced generalization is beneficial to realize the real-time and robust smart control of MR systems.

magnetorheological damper; nonparametric model; NARX network; Bayesian regularization; generalization

国家自然科学基金(51608128)；福州大学科研启动基金(510110)；福建省教育厅科技项目(JA15098)；福建省自然科学基金资助项目(2016J05123)

2016-01-05 修改稿收到日期： 2016-07-04

陈昭晖 男，博士，助理研究员，1982年10月生

TU352；TB535

A

10.13465/j.cnki.jvs.2017.06.022