2N和N+1支撑三跨转子在三种联轴器下的振动特性实验研究

胡航领，何立东，王晨阳

(北京化工大学 化工安全教育部工程研究中心，北京 100029)

2N和N+1支撑三跨转子在三种联轴器下的振动特性实验研究

胡航领，何立东，王晨阳

(北京化工大学 化工安全教育部工程研究中心，北京 100029)

针对2N和N+1支撑转子轴系通过临界转速时振动过大的问题，搭建了2N(三跨六支撑)和N+1支撑(三跨四支撑)轴系实验台，模拟开机启动过程，试验研究两实验台轴系分别使用刚性、膜片和弹性联轴器时的振动特性。结果表明，N+1支撑方式可降低原2N支撑轴系对应的临界转速，且N+1支撑轴系各转轴的耦合更为强烈，容易激起相邻转轴的振动。使用刚性较小的联轴器时，2N 和N+1支撑轴系振动均趋于平稳，说明轴系的耦合减弱，如2N支撑轴系测点1使用弹性联轴器时相比于使用刚性联轴器时在临界转速附近振动幅值降幅达50%。

2N支撑轴系； N+1支撑轴系； 临界转速； 共振峰值

通过联轴器串联的多跨运行方式普遍应用于电力、石化等领域的许多大型旋转机械中，如低压和高压离心压缩机串联机组。随着旋转机械对节能降耗和生产效率要求的不断提高，近年来国内外出现了运行效率高的新型N+1支撑轴系。N+1 支撑轴系在旋转机械快速启动、高效运行、节能环保、经济可靠等方面较传统的2N支撑轴系结构优势明显。

N+1支撑轴系采取的是N个转子只有N+1个支撑的特殊多转子轴系结构，与常用的2N支撑轴系结构相比，其结构优点主要有[1-4]：轴承数量少，轴系结构紧凑；投资成本低，经济效益好；便于对中调试安装，基础变形影响较少；轴承承载负荷重，摩擦功耗损失少，是一种高效低能耗的轴系结构。由于N+1支撑轴系结构紧凑、转子多、轴承少、承载重等轴系布置和结构特点，同时轴系转子间动力学耦合性强、相互关联大、振动复杂，很显然其动力学特性不同于传统2N支撑轴系结构，给这类轴系动力学特性分析带来新的挑战。近年来，国内外出现了对N+1支撑轴系的动力特性研究。张优云等[5]进行了双跨三支承转子系统耦合实验，分析轴系不同位置的振动信号，研究双侧转子对中间轴颈振动的影响。罗跃钢等[6-7]建立带有支承松动故障的双跨三支承弹性转子-轴承系统非线性动力学模型，分析松动质量对系统非线性特性的影响和故障特征。SPRINGER[8]研究了双跨三支承转子中间轴承的标高变化对各轴承负荷分配和不平衡响应的影响。

旋转机械在运行过程中，特别是对于N+1支撑轴系，其工作转速通常高于一阶临界转速，在开、停车阶段必须经过临界转速，经严格动平衡后串联的各跨转子在运转时仍可能发生强烈振动。消除轴系不平衡振动的常用措施是进行现场动平衡，但是需要反复启、停机组，造成严重的经济损失[9-12]。因此研究2N与N+1支撑轴系的振动特性具有十分重要的意义。

本文设计了使用多种联轴器连接的轴系结构和实验方案，搭建了2N(三跨六支撑)及N+1(三跨四支撑)轴系实验台，开展了在刚性联轴器、膜片联轴器和弹性联轴器连接时，2N和N+1支撑轴系的振动规律实验研究。

1 联轴器耦合的转子系统动力学特性分析

将联轴器耦合的转子系统离散为多自由度系统，转子系统在不平衡力作用下的动力学方程可表示为

(1)

联轴器的耦合作用对于转子系统来说是内力，但对于某一单个转子来说是外力，则对于第n个转子在不平衡力作用下的动力学方程可表示为[13]

(2)

将各个转子的振动方程合并，可得多转子系统耦合的振动方程为

(3)

由式(1)和式(3)可得C=C′+Cc，K=K′+Kc，Fc可表示为

(4)

式中：Kc和Cc为联轴器耦合的多转子系统的总体耦合刚度矩阵和总体耦合阻尼矩阵。

由以上分析可得，联轴器的耦合作用与其刚度有关，刚度越大，轴系的耦合作用则越为强烈。

2 2N和N+1支撑转子振动特性实验研究

2.1 联轴器参数

轴系中连接各转子的联轴器采用三种结构类型，分别为套筒式刚性联轴器、单节夹紧螺丝固定式膜片联轴器和夹紧螺丝固定平行式弹性联轴器，联轴器刚度依次递减。刚性联轴器承受负载时无任何回转间隙，膜片联轴器和弹性联轴器可补偿径向、角向和轴向偏差。联轴器具体参数,如表1所示。

表1 联轴器基本参数Tab.1 Parameters of coupling

2.2 实验台参数

本文搭建了2N和N+1支撑三跨转子实验台如图1所示，分别采用刚性联轴器、膜片联轴器和弹性联轴器进行了2N和N+1支撑轴系的振动规律实验研究。各转轴长600 mm，轴直径15 mm，支撑跨距480 mm；各跨均为双盘转子，转盘质量6.89 kg，转盘直径200 mm。实验台的转子支撑结构可以上下移动，能用于调节各转子对中。本实验进行N+1支撑实验时，只需用到四个支撑，此时在2N支撑的基础上通过降低支撑3与支撑5使轴与支撑脱开，可得到三跨四支撑轴系。其中测点1为轴1所在支撑(支撑2)；测点2为轴2所在支撑(支撑4)；测点3为轴3所在支撑(支撑6)。

实验用测试系统为LC-8000 系列多通道振动监测故障诊断系统，包含8个输入通道和专用振动信号处理采集板。本实验选择的是测量支撑摆架水平振动加速度，加速度传感器的采样频率为1 kHz。实验时数据经由加速度传感器和光电传感器采集信号，调用LC8000采集的时域波形中的有效值进行记录，约0.8 s记录一个数据。

2.3 2N和N+1支撑轴系振动特性实验

2.3.1 刚性联轴器连接的2N和N+1支撑三跨轴系振动实验研究

轴系转速由0升到2 000 r/min，分别采集了两种支撑方式的测点1、测点2和测点3的振动数据，如图2所示。

从图2的振动数据可得刚性联轴器连接的三跨转子轴系的振动特性为：2N支撑轴系的一阶临界转速约为1 890 r/min，轴系在一阶临界转速时，三个测点振动较大，产生了明显的峰值。N+1支撑轴系的一阶临界转速约为1 150 r/min，此时为轴3的振动引起的，测点3的振动较大，同时激起了轴1和轴2的振动，三个测点的振动都有明显的峰值；二阶临界转速约为1 560 r/min，此时为轴2的振动引起的，由于轴3的耦合较严重，测点3的振动峰值较大；三阶临界转速约为1 850 r/min，此时为轴1的振动引起的，由于三轴之间的振动耦合，三个测点振动都较大，出现了明显的峰值。

(a) 三跨六支撑轴系示意图

(b) 三跨四支撑轴系示意图

(c) 实物图

(a) 测点1

(b) 测点2

(c) 测点3

通过测点1、测点2、测点3振动数据的比较可知，N+1支撑方式可降低原2N支撑轴系对应的临界转速，这是由于N+1支撑约束刚度小于2N支撑。N+1支撑轴系各转轴的耦合较为强烈，容易激起相邻转轴的振动。使用刚性联轴器时N+1支撑轴系在临界转速附近振动峰值大于2N支撑轴系。

2.3.2 膜片联轴器连接的2N和N+1支撑三跨轴系振动实验研究

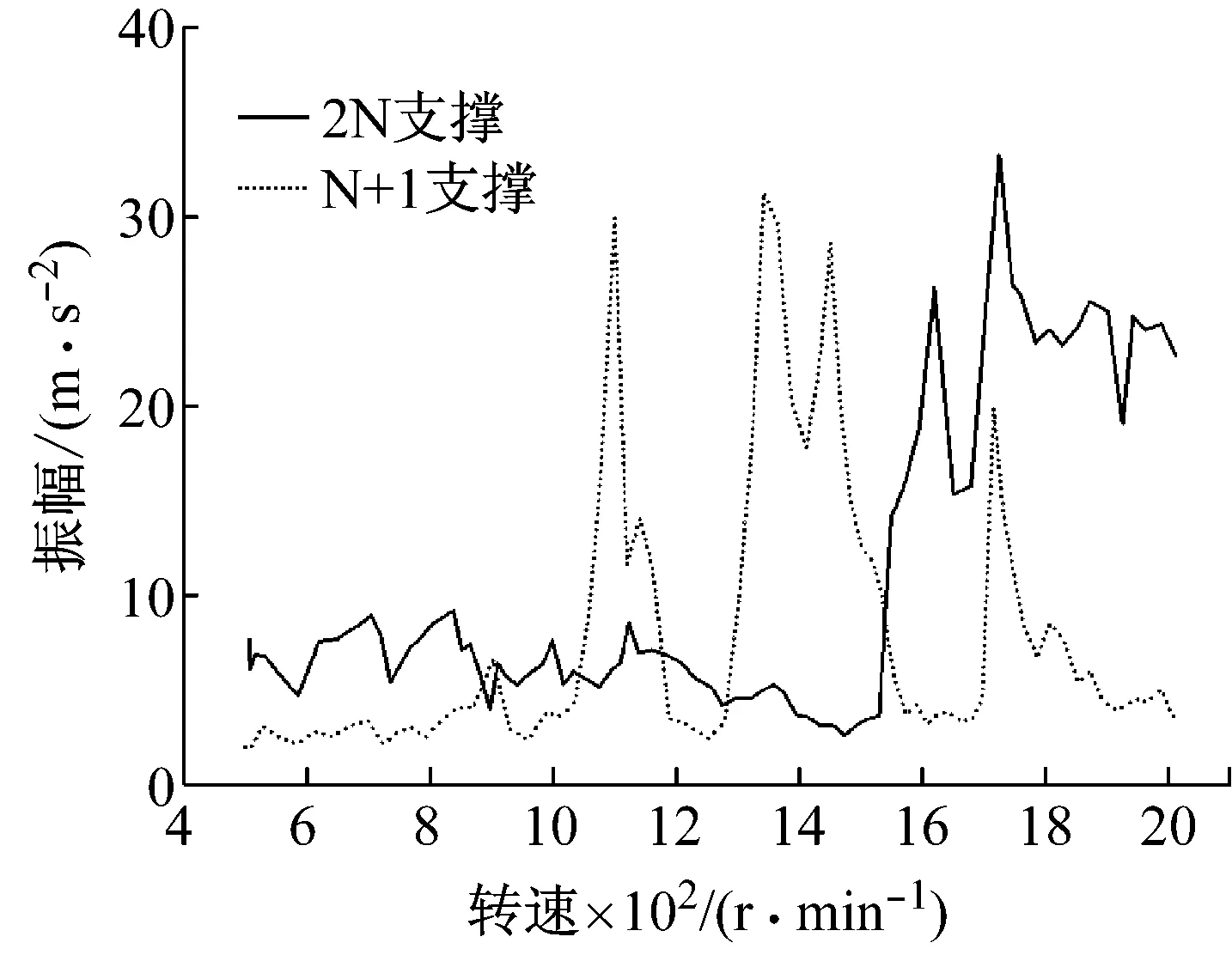
由于刚性联轴器连接的N+1支撑轴系耦合较为强烈，可选用刚性较小的联轴器，如膜片联轴器。转速由0升到2 000 r/min，分别采集了两种支撑方式的测点1、测点2和测点3的振动数据，如图3所示。

(a) 测点1

(b) 测点2

(c) 测点3

从图3的振动数据可得膜片联轴器连接的三跨转子轴系振动特性为：2N支撑轴系的一阶临界转速约为1 750 r/min，轴系在一阶临界转速时，三个测点均有明显的振动峰值。N+1支撑轴系的一阶临界转速约为1 100 r/min，此时为轴3的振动引起的，同时激起了轴1和轴2的振动，三个测点的振动都有明显的峰值；二阶临界转速约为1 350 r/min，此时为轴2的振动引起的，由于轴2和轴3的耦合较严重，测点2和测点3的振动峰值明显大于测点1；三阶临界转速约为1 700 r/min，此时为轴1的振动引起的，由于三轴之间的振动耦合，三个测点振动都较大，出现了明显的峰值。

通过测点1、测点2、测点3振动数据的比较可知，N+1支撑方式对应的临界转速小于2N支撑轴系，与使用刚性联轴器时相同，均是由于N+1支撑约束刚度小于2N支撑造成的。N+1支撑轴系各转轴的耦合较为强烈，容易激起相邻转轴的振动。使用膜片联轴器时，N+1支撑轴系在临界转速附近振动峰值略小于2N支撑轴系。

2.3.3 弹性联轴器连接的2N和N+1支撑三跨轴系振动实验研究

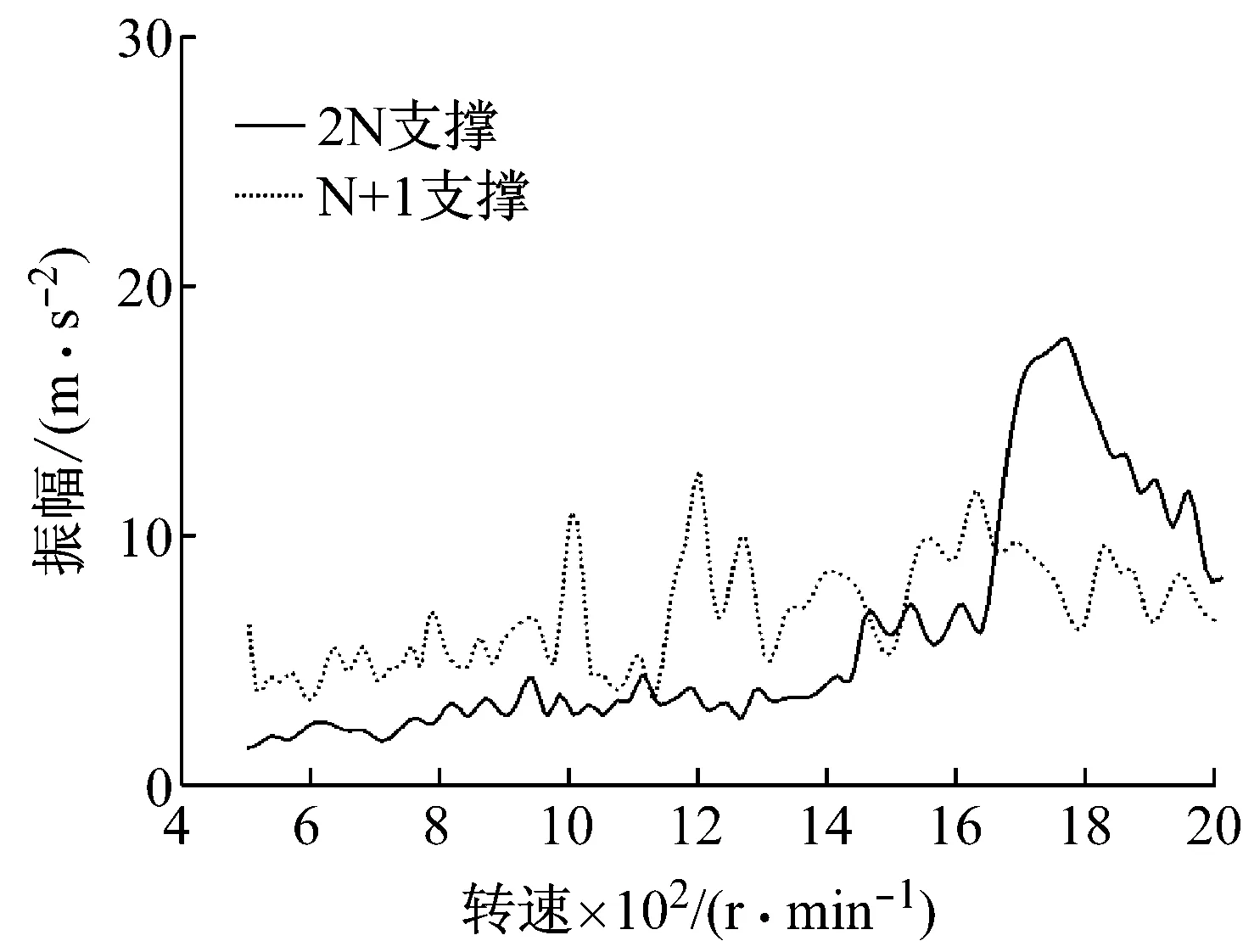
进一步选用刚性更小的联轴器进行实验，如弹性联轴器。轴系转速由0升到2 000 r/min，分别采集了两种支撑方式的测点1、测点2和测点3的振动数据如图4所示。

(a) 测点1

(b) 测点2

(c) 测点3

从图4的振动数据可得弹性联轴器连接的三跨转子轴系振动特性为：2N支撑轴系的一阶临界转速约为1 700 r/min，轴系在一阶临界转速时，三个测点出现了振动峰值。N+1支撑轴系的一阶临界转速约为1 020 r/min，此时为轴3的振动引起的，由于轴2与轴3之间的耦合较严重，测点2出现了明显的振动峰值；二阶临界转速约为1 200 r/min，此时为轴2的振动引起的；三阶临界转速约为1 650 r/min，此时为轴1的振动引起的，由于三轴之间的振动耦合，三个测点都出现了振动峰值，其中测点2的振动峰值较测点1与测点3大。

通过测点1、测点2、测点3振动数据的比较可知，使用弹性联轴器时，N+1支撑约束刚度小于2N支撑，N+1支撑方式对应的临界转速仍小于原2N支撑。采用弹性联轴器时，N+1支撑轴系在临界转速附近振动峰值明显小于2N支撑轴系。

3 不同联轴器对轴系振动特性影响研究

综合上述三组实验，研究三种联轴器对轴系振动特性的影响。以测点1为例，分别比较2N和N+1支撑轴系使用三种联轴器时在临界共振区的振动，具体数据如表2和表3所示。表2为2N支撑轴系一阶临界共振区的振动峰值，表3为N+1支撑轴系三阶临界共振区的振动峰值。

表2 2N支撑轴系测点1的振动数据Tab.2 Vibration data of 2N support rotors at Point 1

表3 N+1支撑轴系测点1的振动数据Tab.3 Vibration data of N+1 support rotors at Point 1

由表2和表3可知，使用刚性较小的联轴器时，2N和N+1支撑轴系振动均趋于平稳，说明轴系的耦合减弱，轴系在临界共振区的振动大小按刚性联轴器、膜片联轴器、弹性联轴器的顺序依次减小。由于三跨转子轴系各转子施加的不平衡量相同，刚性联轴器在临界共振区的振动最大，说明刚性联轴器连接的三跨轴系三轴之间的耦合最为强烈。

4 结 论

(1) N+1支撑方式可降低原2N支撑轴系对应的临界转速，且N+1支撑轴系各转轴的耦合更为强烈，容易激起相邻转轴的振动。

(2) 使用刚性较小的联轴器时，2N 和N+1支撑轴系振动均趋于平稳，轴系在临界共振区的振动大小按刚性联轴器、膜片联轴器、弹性联轴器的顺序依次减小。

[1] 高庆水，邓小文，张楚，等.单支撑1 000 MW超超临界汽轮机轴系不平衡响应分析[J].振动与冲击，2014，33(14)：201-205.

GAO Qingshui, DENG Xiaowen, ZHANG Chu, et al.Unbalance response of 1 000 MW ultra supercritical turbine with single bearing support[J].Journal of Vibration and Shock, 2014, 33(14): 201-205.

[2] 吴文健，童小忠，应光耀，等.单支撑超超临界1 000 MW汽轮发电机组振动诊断与处理[J].浙江电力，2011，10：32-36.

WU Wenjian, TONG Xiaozhong, YING Guangyao, et al.Diagnosis and treatment for vibration of ultra-supercritical 1 000 MW steam turbine units supported by single bearing[J].Zhejiang Electric Power, 2011, 10:32-36.

[3] 张学延，张卫军，葛祥，等.西门子技术1 000 MW 超超临界机组轴系振动问题[J].中国电力，2012，45(5)：68-72.

ZHANG Xueyan, ZHANG Weijun, GE Xiang, et al.Vibration of turbine shafting in 1 000 MW ultra supercritical unit with Siemens technology[J].China Electric Power, 2012,45(5):68-72.

[4] 武秀峰.我国超超临界机组参数与结构选型的研究[J].电力科学与工程，2008，24(9)：45-50.

WU Xiufeng.Research on parameter and construction selection of ultra-supercritical unit in China[J].Electric Power Science and Engineering, 2008,24(9): 45-50.

[5] 赵荣珍，张优云，孟凡明.双跨转子轴承系统耦合实验研究[J].润滑与密封，2003，3：7-8.

ZHAO Rongzhen, ZHANG Youyun, MENG Fanming.Experimental study of coupling effects between two spans in rotor-bearing system[J].Lubrication and Sealing, 2003, 3:7-8.

[6] 罗跃纲，杜元虎，刘晓东，等.双跨转子系统支承松动的动态特性及故障特征研究[J].机械强度，2006，28(3)：327-331.

LUO Yuegang, DU Yuanhu, LIU Xiaodong, et al.Study on dynamics and fault characteristics of two-span rotor-bearing system with pedestal looseness[J].Journal of Mechanical Strength, 2006, 28(3):327-331.

[7] 罗跃纲，闻邦椿.双跨松动转子-轴承系统周期运动稳定性[J].振动与冲击, 2007，26(8)：9-12.

LUO Yuegang, WEN Bangchun.Stability of two-span rotor-bearing system with pedestal looseness fault[J].Journal of Vibration and Shock, 2007, 26(8):9-12.

[8] SPRINGER H, ECKER H, GUNTER E J.Nonlinear unbalance response and stability thresholds of a warped multi-mass rotor inmisaligned bearings[J].IMeche,1984,C295/84.

[9] 高金吉，缪红燕，徐鸿，等.多转子轴系优化耦联及其不平衡响应有限元分析[J].振动与冲击，2005，24(2)：1-4.

GAO Jinji, MIAO Hongyan, XU Hong, et al.Multi-rotors system coupling optimization and unbalance response analysis with finite element method[J].Journal of Vibration and Shock, 2002, 24(2): 1-4.

[10] 缪红燕，高金吉，徐鸿，等.基于有限元法的柔性转子虚拟动平衡研究[J].振动、测试与诊断，2004，24(3)：14-18.

MIAO Hongyan, GAO Jinji, XU Hong, et al.A study of virtual balancing of flexible rotor based on finite element method[J].Journal of Vibration, Measurement & Diagnosis, 2004, 24(3): 14-18.

[11] BISHOP R E D, GLADWELL G M L.The vibration and balancing of an unbalance flexible rotor[J].Journal of Mechanical Engineering for Science, 1959 (1): 66-77.

[12] LUND J W, TONNESEN J.Analyses and experiments on multiplane balancing of a flexible rotor[J].American Society of Mechanical Engineers Journal of Engineering for Industry, 1972,94: 233-242.

[13] 范叶森，王三民，杨振，等.挠性联轴器耦合多转子系统振动分析的总体耦合矩阵法[J].机械科学与技术，2010，29(5)：584-588.

FAN Yesen, WANG Sanmin, YANG Zhen, et al.A whole coupled matrixmethod for vibration analysis of multi-rotor system with flexible couplings[J].Mechanical Science and Techmology for Aerospace Engineering, 2010, 29(5): 584-588.

Tests for vibration characteristics of a N-span & 2N-support rotor system and a N-span & (N+1)-support one connected with three kinds of coupling

HU Hangling, HE Lidong, WANG Chenyang

(Engineering Research Center of Chemical Technology and Safety, Ministry of Education Beijing University of Chemical Technology, Beijing 100029, China)

In order to solve the problem that 2 N-span & 2N-support rotor system and a N-span & (N+1)-support one have too large vibrations when passing through their critical speeds, their test benches were established to simulate their operation process.The vibration characteristics of two rotor systems connected with three kinds of coupling were studied.The results showed that if the 2N-support mode is replaced by the (N+1)-support one, the critical speeds of the rotor system can be reduced; the coupling among rotating shafts of the rotor system with (N+1)-support mode is stronger to easily excite vibrations of adjacent shafts; the vibrations of the 2N-support rotor system and the (N+1)-support one tend to be steady when connected with smaller stiffness couplings, so the coupling among rotating shafts tends to be weaker; for an example, the vibration amplitude of the measurement point 1 on the rotor system with 2N-support when connected with flexible couplings is reduced by 50% near the critical speeds of the system, compared with that when connected with rigid couplings.

2N-support rotor; (N+1)-support rotor; critical speed; resonance peak

国家重点基础研究发展计划(“973”计划)(2012CB026000)；教育部博士点基金(20110010110009)

2015-08-17 修改稿收到日期：2016-09-07

胡航领 男，硕士生，1991年生

何立东 男，教授，博士生导师，1963年生

TK14； TB535+.1

A

10.13465/j.cnki.jvs.2017.05.026