基于QGA优化广义S变换的滚动轴承故障特征提取
2017-04-10刘树林张宏利
王 波, 刘树林, 张宏利
(1.滁州学院 机械与汽车工程学院, 安徽 滁州 239000; 2.上海大学 机电工程与自动化学院, 上海 200072)
基于QGA优化广义S变换的滚动轴承故障特征提取
王 波1, 刘树林2, 张宏利2
(1.滁州学院 机械与汽车工程学院, 安徽 滁州 239000; 2.上海大学 机电工程与自动化学院, 上海 200072)
考虑到实际工程环境中噪声对故障特征提取的影响,提出了基于量子遗传算法(QGA)优化广义S变换的滚动轴承故障特征提取方法。该方法以时频分布集中程度为评价标准,首先采用量子遗传算法自适应地选取广义S变换中最优窗口控制参数,然后提取信号变换后复时频矩阵的模向量作为滚动轴承故障特征向量。利用该方法提取的滚动轴承故障特征与其它故障特征进行故障识别对比研究,实验结果表明该方法能够更准确地提取出故障特征,验证了方法的优越性。此外,对不同噪声强度背景下的滚动轴承振动信号进行故障特征提取,诊断结果进一步显示所提方法具有良好的抗噪性和健壮性。
广义S变换; 量子遗传算法; 滚动轴承; 故障诊断; 特征提取
滚动轴承作为旋转机械中的一个重要的零部件,其故障的产生直接导致机械性能的下降甚至发生事故,因此,滚动轴承的故障诊断研究一直是研究的热点。信号处理技术是故障特征提取的基础,不同的信号处理技术可以提取出信号不同的故障特征信息。特征提取的优劣直接影响到最终智能故障诊断结果的准确性。
滚动轴承振动信号是一种非平稳、非线性信号。采用小波变换或小波包变换提取信号中的能量作为故障特征,在滚动轴承故障诊断中得到了应用[1-3]。然而小波变换及小波包变换不能自适应地分解信号,并且小波基和小波包基的选择以及分解层数的确定仍然是个难题。自适应信号处理方法EMD和EEMD的提出克服了小波变换及小波包变换的这些缺点,也被应用到了滚动轴承故障诊断中。然而EMD存在模态混叠效应,EEMD虽然克服了模态混叠效应的产生,但EEMD中的白噪声幅值和迭代次数也需要经验性的设定,同样也影响故障特征的提取。S变换(ST)是由STOCKWELL等[6]提出的一种信号时频分析方法,结合了连续小波变换(CWT)及短时傅里叶变换(STFT)的优点,具有良好的时频分析能力,特别适用于处理非平稳信号,且对噪声不敏感。
考虑到实际工程环境下噪声对故障特征提取的影响,提出一种基于广义S变换(GST)的滚动轴承故障提取方法。该方法以时频分布集中程度为评价标准,采用量子遗传算法(QGA)自适应选取广义S变换中最优窗口控制参数,以达到最优故障特征提取。分别采用S变换和QGA优化后的广义S变换对滚动轴承振动信号进行处理,从能量的集聚性定量分析所提方法的优越性。同时,将提取的滚动轴承故障特征向量与EEMD能量及小波包能量进行了实验对比研究,分别输入到支持向量机(SVM)及相关向量机(RVM)中进行故障识别。实验结果表明了所提方法的可行性、有效性及优越性。
1 理论分析
S变换可以看作成一个可变窗口函数的短时傅里叶变换,也可以看作是连续小波变换的扩展。S变换同时结合了两种方法的优点,既保留了短时傅里叶变换中信号的相位信息,同时也提供了可变的信号分解尺度,特别适合于处理非平稳信号[7-11]。
滚动轴承的振动信号是一种典型的非线性、非平稳信号,设滚动轴承的振动信号为x(t)。
定义 1 对于滚动轴承的振动信号x(t),对x(t)进行STFT变换,如式(1)所示[11-12]:
(1)
式中:τ为频谱位置对应的时间;f为信号频率;g(t)为窗口函数。
定义 2 经S变换后的信号可定义如式(2)所示:
(2)
式中,w(t-τ)为高斯窗口,表示为
(3)
(4)
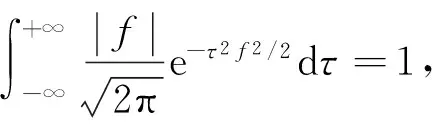
(5)
由此可见,S变换的本质是用高斯窗口函数替代窗口函数g(t),可视为STFT采用高斯窗口函数的一个特例。S变换相对于STFT的关键优点即为标准差σ是频率f的函数,即式(4)所示。高斯窗口的高度和宽度随频率而变化,克服了STFT窗口高度和宽度固定的缺点。高斯窗口函数具有良好的调节性,在信号的低频段具有更高的分辨率,而在高频段具有更好的时间分辨率。
虽然S变换在一些领域得到了应用,但S变换的缺点是在处理信号中,对于所有的频段都设置不变的标准差,其值随频率变化的趋势不变,影响了S变换在信号分析中的适应性。同时,在一些领域的实际应用中发现,采用S变换对信号进行时频分析存在着时频能量不聚集等缺陷[13]。针对S变换在实际应用中存在的不足和缺陷,提出的广义 S变换改进了S变换的不足,对式(5)进行了改进:
(6)
即给定一个控制参数p,通过控制标准差的大小控制窗口函数的宽度,具有更优的时频能量聚集性。
因此,本文尝试采用广义S变换对滚动轴承振动信号处理,以便于提取更优的故障特征。此时经过广义S变换后的滚动轴承振动信号为
(7)
当p=1时,即为标准S变换。
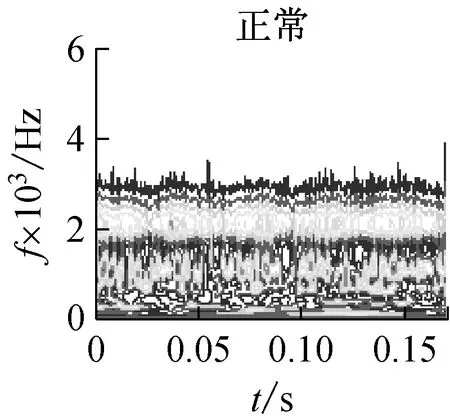
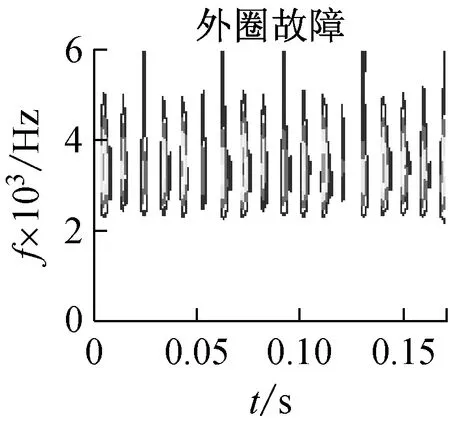
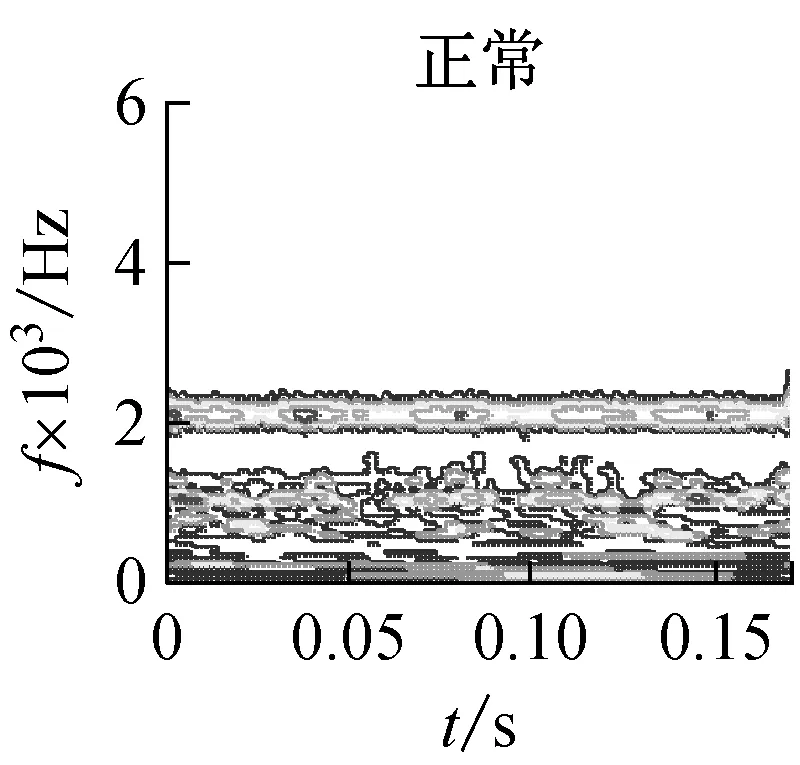
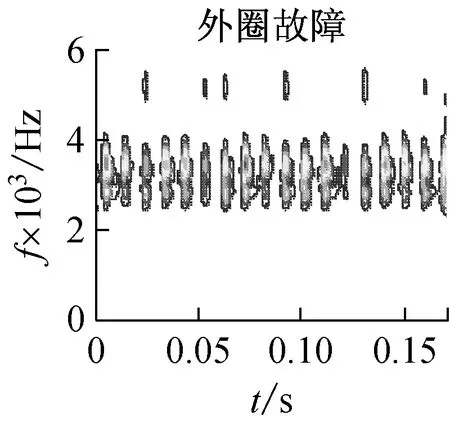
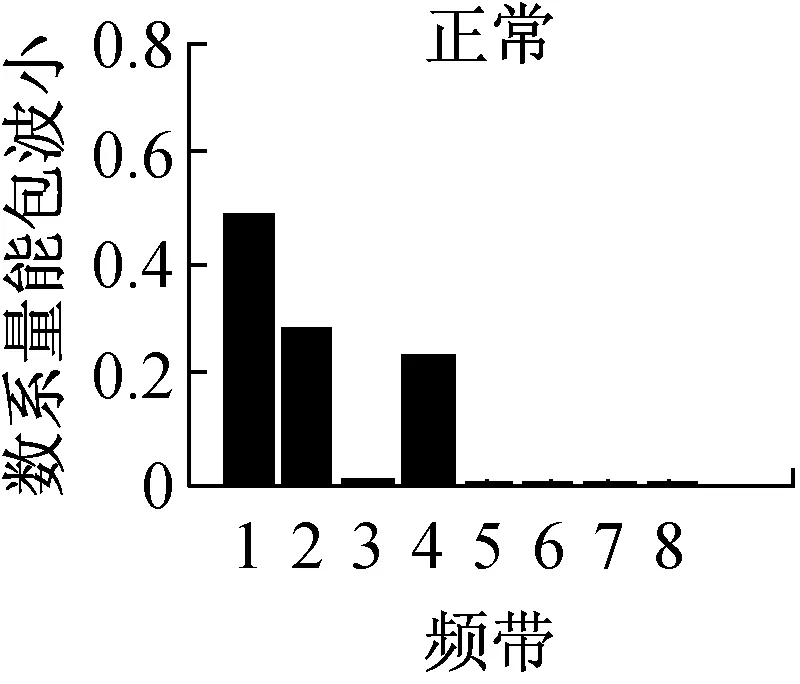
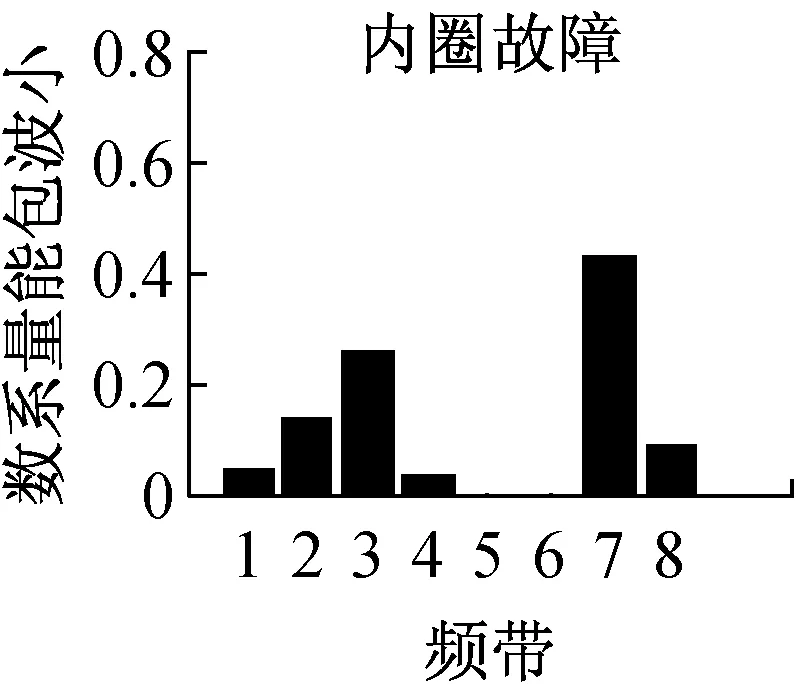
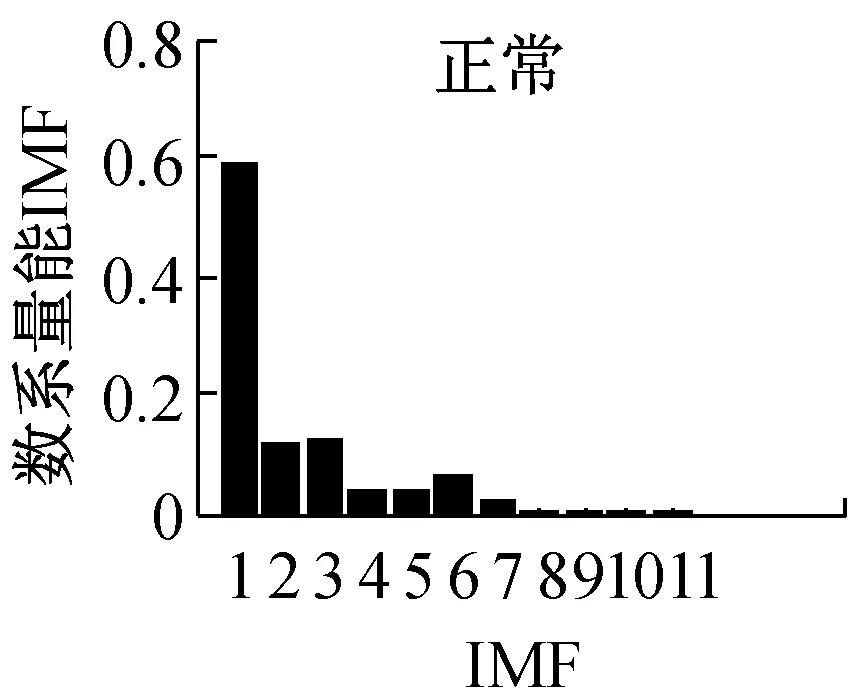
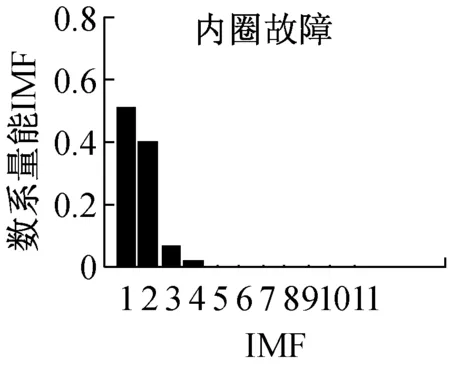
从上述分析可见,广义S变换中窗口控制参数p的选择至关重要。根据文献[14]的分析,通常情况下,0 为了提取基于广义S变换的滚动轴承最优故障特征向量,提出了一种量子遗传算法(QGA)自适应选取参数p的故障特征提取方法,以时频分布集中程度Mx(p)定量的评价p的选择[15] (8) 振动信号经过广义S变换后的结果为复时频矩阵,可用时频图像来表示。因此,须提取复时频矩阵中的信息量作为故障特征向量,以便输入到故障识别器中进行最终的识别。 2.1 量子遗传算法 量子遗传算法(QGA)是较新颖的群智能算法[16],在传统的遗传算法(GA)中引入量子计算的概率和机制,其染色体用量子比特取代GA中的二进制串,特殊的量子比特表示形式提高了种群的多样性。染色体以概率幅的形式表示某种状态的信息。采用量子比特编码,使得一个染色体可以同时表达多个量子态的叠加,即仅通过一个小数量种群的量子个体来代替传统数量较大的个体。通过量子门操作驱动个体向最优解进化。此进化策略使得量子遗传算法拥有良好的全局寻优能力,同时利用量子计算具有天然的并行性,加快了算法的收敛速度,具有更好的多样性特征以及更佳的收敛性。因此,考虑到故障特征提取过程中计算的复杂性,为了提高优化的速度及准确性,本文以滚动轴承振动信号经过广义S变换后的时频分布集中程度Mx(p)为适应度,采用QGA自适应地选取最优控制参数p。 2.2 故障特征提取具体过程描述 滚动轴承故障特征提取具体过程如下: (1) 对控制参数p在(0,1]范围内进行量子比特编码,初始化p值,然后对振动信号x(t)进行广义S变换。 (2) 对变换后的信号求归一化能量[15]: (9) (3) 根据公式(8)计算此时的评价值Mx(p)。 (4) 根据量子遗传算法进行更新,重新计算不同p值下的Mx(p)。此时,选取Mx(p)作为控制参数p的适应度函数,即 f(p)=Mx(p) (10) 迭代计算出Mx(p)最小时的p值作为最优值popt。 (5) 提取popt下x(t)经广义S变换后的复时频矩阵,记为S[a,b]。其列对应时间,行对应频率。 (6) 对矩阵S[a,b]中的各个值求模,求得的结果为一个模矩阵,记为S[m,n]。其列向量表示信号某一时刻的幅值随频率变化的分布,其行向量表示信号某一频率处的幅值随时间变化的分布。 具体的基于量子遗传算法优化控制参数p的过程及参数设置见本文2.3、2.4节。 2.3 控制参数优化过程描述 图1给出了基于QGA自适应选取最优广义S变换控制参数p的流程图。具体的优化过程描述如下: (1) 将控制参数p作为一个染色体。随机产生N条以量子比特为编码的染色体对控制参数进行编码,构成初始种群 (4) 通过量子门进化操作更新获得新的种群P(1)。选择量子旋转门使算法朝着最优解的方向搜索,此时 (5) 判断是否满足设置的终止条件,若满足,则终止算法;否则,继续以下步骤。 (6) 令t=t+1,并返回(2)。以此不断迭代更新,最终自适应地获取广义S变换的最优控制参数值。 2.4 关键参数设置描述 在利用QGA优化广义S变换控制参数值之前,需对算法中的关键参数进行初始化,本文对参数进行了如下设置: (1) 初始化种群。P(0)中各个(α,β)均初始化为(1/sqrt(2),1/sqrt(2)),表示在初始进化时一个染色体所有状态均以相同的概率进行叠加。量子染色体的长度n=20,染色体条数N=20,即种群大小。最大迭代次数maxgen=50。 图1 基于QGA优化广义S变换参数p的流程图Fig.1 The flow chart of the parameter optimization of generalized S transform based on QGA 3.1 实验数据 滚动轴承故障试验的数据来自于美国Case Western Reserve University轴承数据中心。实验采用的轴承型号为6205-2RS JEM SKF深沟球轴承。实验中分别获取不同载荷 (0 ph,1 ph,3 ph)、不同故障程度下三种轴承故障的振动测试数据以及正常轴承数据。三种故障分别为外圈点蚀故障、内圈点蚀故障及滚动体点蚀故障,其中点蚀故障通过电火花加工生成。 本文选用载荷为3Hp下感应电机驱动端的滚动轴承振动数据为实验数据,振动信号采样频率为12 000 Hz,滚动轴承的旋转速度1 730 r/min,故障程度为0.177 8×0.279 4 mm。 美国Case Western Reserve University轴承数据中心环境较好,测试的振动数据中所含噪声也非常小。然而在工程实际中,所测得的振动数据会受到外部环境的影响,振动信号比较复杂。为了模拟工程实际,在原始的滚动轴承振动信号中添加了信噪比为40 dB的高斯白噪声。实验在CPU速度为3.30 GHz,内存为4 GB的计算机下进行。 3.2 效果分析 为了分析所提出的故障特征提取方法在噪声环境下的可行性和优越性,通过实验进行了对比分析。分别采QGA优化popt下的广义S变换和S变换(p=1),按所提方法对滚动轴承振动信号进行处理。 图2是滚动轴承四种状态下的S变换时频图,图3是滚动轴承四种状态最优控制参数下的广义S变换时频图。对比分析图2和图3,从时频平面上能量聚集性可见,采用标准S变换与采用QGA优化popt下的广义S变换对滚动轴承振动信号进行时频处理相比,后者在时频平面上聚集性更好。同时,以滚动体故障为振动信号为例,根据式(8)可得两种方法下的能量集中程度值M1= 0.963,M2= 0.561(即M2 为了进一步验证所提方法的有效性和优越性,同时提取滚动轴承小波包能量及EEMD能量故障特征,将三种故障特征分别输入到不同的故障识别器中进行故障识别对比实验。 选取‘db16’小波包作为小波包能量特征提取时的小波包。对滚动轴承振动信号进行小波包3层分解得到8个分解频带。图4显示了归一化后的滚动轴承4种状态下的小波包能量频谱图。 设置EEMD的迭代次数为100,白噪声的幅值为0.2。对滚动轴承振动信号进行EEMD分解,提取4种状态下的IMF能量作为滚动轴承的故障特征。图5显示了归一化后滚动轴承种状态下的IMF能量频谱图。 在此每个故障样本由2 048个连续采样数据构成,每种滚动轴承状态下有59个样本。每种状态下任意选取20个样本作为诊断模型的训练样本(共80个),剩余的样本(共156个)构成模型的测试样本,以标准RVM和SVM为故障识别器。 最终的实验结果见表1,实验结果为100次故障诊断实验下的平均值,其中Svs、Rvs分别表示故障识别器训练阶段所需的支持向量个数及相关向量个数。在此,RVM和SVM均采用RBF核函数。根据所提方法提取的滚动轴承故障特征向量S[m,n]维数较高,增加了故障诊断模型计算的复杂度。为了降低计算的复杂度,对三种不同故障特征均采用核主成分分析(KPCA)进行降维预处理。 表1 添加噪声后不同特征的故障识别结果Tab.1 The fault recognition results based on different feature 从表1可见,无论采用RVM或SVM作为最终的识别器,所提方法提取的故障特征均获得了最高的故障诊断率。分析其原因,主要有以下两个原因:首先,由于广义S变换本身对噪声不敏感,在背景噪声较强的情况下能够提取到更准确的故障特征。另外,采用了QGA自适应地选取了最优popt值,更加精确地提取出滚动轴承的故障特征。同时,从表1可见,采用所提方法提取的故障特征作为输入特征向量,RVM和SVM在模型的训练阶段均获得了最少的支持向量个数(Svs)及相关向量个数(Rvs),提高了对未知故障样本识别的效率。 为了进一步分析基于广义S变换的故障特征提取方法的健壮性,分别对原始故障数据添加不同信噪比的噪声,采用三种不同方法提取故障特征向量,并采用SVM及RVM对其进行故障识别,对比分析随着添加高斯白噪声信噪比的降低(噪声强度越来越大),故障诊断准确率的变化情况,实验结果如图6、图7所示。 图6 故障诊断率随噪声增强的变换趋势(RVM)Fig.6 Transformation trend of fault diagnosis accuracy with the noise enhancement(SVM) 图7 故障诊断率随噪声增强的变换趋势(RVM)Fig.7 Transformation trend of fault diagnosis accuracy with the noise enhancement(RVM) 从图6、图7可以看出,随着信噪比从100 dB以10 dB的间隔逐渐减少时,采用所提出的基于广义S变换的故障特征提取方法,无论采用RVM还是SVM作为最终的故障识别器,其故障诊断率变换趋势相对较小,说明了该方法提取出的故障特征对噪声不敏感,克服了噪声对故障特征提取准确性的影响,具有良好的抗噪性,且健壮性更好。 提出了一种基于QGA优化广义S变换的滚动轴承故障特征提取方法,利用了QGA具有全局搜索寻优能力强、收敛速度快及种群多样性等特点,自适应地选取最优窗口控制参数,克服了广义S变换窗口控制参数选择的不确定性。通过滚动轴承故障实例诊断实验分析,从能量聚集性角度可以看出,与采用S变换相比,采用QGA优化popt下的广义S变换具有更佳时频分布聚集性,即更加容易区分出滚动轴承的不同状态。提取振动信号变换后复时频矩阵中的信息量作为特征向量,同时提取小波包能量及EEMD能量作为滚动轴承故障特征,分别输入到RVM及SVM中进行故障识别,进行了对比研究。实验结果表明,采用所提方法提取的故障特征获得了最高的故障识别率,同时训练出的故障识别决策函数更为简单,提高了未知故障识别的效率。通过不同噪声强度下滚动轴承故障识别实验,表明本文所提出的故障特征提取方法具有良好的抗噪性和健壮性,更加适合于实际工程环境下的滚动轴承故障特征提取。 [1] EKICI S, YILDIRIM S, POYRAZ M.Energy and entropy-based feature extraction for locating fault on transmission lines by using neural network and wavelet packet decomposition[J].Expert Systems with Applications, 2008,34(4):2937-2944. [2] 李辉, 郑海起, 唐力伟.基于双树复小波包峭度图的轴承故障诊断研究[J].振动与冲击, 2012,31(10):13-18. LI Hui, ZHENG Haiqi, TANG Liwei.Bearing fault diagnosis based on kurtogram of dual-tree complex wavelet packet tansform[J].Journal of Vibration and Shock, 2012,31(10):13-18. [3] HE Q B.Vibration signal classification by wavelet packet energy flow manifold learning[J].Journal of Sound and Vibration, 2013,332(7):1881-1894. [4] 沈长青, 谢伟达, 朱忠奎, 等.基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J].振动与冲击, 2013,32(2):39-43. SHEN Changqing, Peter W.Tse, ZHU Zhongkui, et al.Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method[J].Journal of Vibration and Shock, 2013,32(2):39-43. [5] 王录雁, 王强, 张梅军, 等.基于 EMD 的滚动轴承故障灰色诊断方法[J].振动与冲击, 2014,33(3):197-202. WANG Luyan, WANG Qiang, ZHANG Meijun,et al.A grey fault diagnosis method for rolling bearings based on EMD[J].Journal of Vibration and Shock, 2014,33(3):197-202. [6] STOCKWELL R G, MANSINHA L, LOWE R P.Localization of the complex spectrum: The S transform[J].Ieee Transactions on Signal Frocessing, 1996,44(4):998-1001. [7] 占勇, 程浩忠, 丁屹峰, 等.基于S变换的电能质量扰动支持向量机分类识别[J].中国电机工程学报, 2005(4):53-58. ZHAN Yong, CHENG Haozhong, DING Yifeng, et al.S-transform-based classification of power quality disturbance signals by support vector machines[J].Proceedings of the CSEE, 2005(4):53-58. [8] DRABYCZ S, STOCKWELL R G, MITCHELL J R.Image texture characterization using the discrete orthonormal S-Transform[J].Journal of Digital Imaging, 2009,22(6):696-708. [9] MAHMOOD M T, CHOI T S.Focus measure based on the energy of high-frequency components in the S transform[J].Optics Letters, 2010,35(8):1272-1274. [10] 蒋模华, 陈文静, 郑志平.基于S变换的解相技术研究[J].光学学报, 2011(4):101-109. JIANG Mohua, CHEN Wenjing, ZHENG Zhiping.Research of phase demodulation technique based on S-transform[J].Optica Sinica, 2011(4):101-109. [11] ZHONG M, CHEN W J, WANG T, et al.Application of two-dimensional S-Transform in fringe pattern analysis[J].Optics and Lasers in Engineering, 2013,51(10):1138-1142. [12] SANCHEZ P, MONTOYA F G, MANZANO-AGUGLIARO F, et al.Genetic algorithm for S-transform optimisation in the analysis and classification of electrical signal perturbations[J].Expert Systems with Applications, 2013,40(17):6766-6777. [13] DASH P K, PANIGRAHI B K, PANDA G.Power quality analysis using S-Transform[J].IEEE Transactions on Power Delivery, 2003,18(2):406-411. [14] DJUROVIC I, SEJDIC E, JIANG J.Frequency-based window width optimization for S-transform[J].Aeu-international Journal of Electronics and Communications, 2008,62(4):245-250. [15] STANKOVIC L.A measure of some time-frequency distributions concentration[J].Signal Processing, 2001,81(3):621-631. [16] 王凌.量子进化算法研究进展[J].控制与决策, 2008,23(12):1321-1326. WANG Ling.Advances in quantum-inspired evolutionary algorithms[J].Control and Decision, 2008,23(12):1321-1326. [17] 杨俊安, 庄镇泉, 史亮.多宇宙并行量子遗传算法[J].电子学报, 2004(6):923-928. YANG Junan, ZHUANG Zhenquan, SHI Liang.Multi-universe parallel quantum genetic algorithm[J].Acta Electronica Sinica, 2004(6):923-928. Fault feature extraction for rolling bearings based on generalized S transformation optimized with Quantum genetic algorithm WANG Bo1, LIU Shulin2, ZHANG Hongli2 (1.School of Mechanical and Automotive Engineering, Chuzhou University, Chuzhou 239000, China;2.School of Mechatronics Engineering and Automation, Shanghai University, Shanghai 200072, China) Considering noise’s effects on fault feature extraction of rolling bearings in practical engineering environment, a novel method for rolling bearing fault feature extraction based on the generalized S transformation optimized with the quantum genetic algorithm (QGA) was proposed.Firstly, the optimal window control parameters of the generalized S transformation were selected adaptively with QGA taking the concentration the level of time-frequency distribution as the evaluation standard.Then the mode vectors of the complex time-frequency matrix formed after fault vibration signals of rolling bearings were transformed with the generalized S transformation were extracted as rolling bearing fault feature vectors.The method was applied to extract rolling bearing fault feature and compared with other methods using fault diagnosis tests.The results showed that the proposed method can extract fault features more accurately than other methods can.Moreover, the fault feature extraction tests of rolling bearing vibration signals under different levels of background noise indicated that the proposed method has a good anti-noise capability and a strong robustness. generalized S transform; quantum genetic algorithm; rolling bearing; fault diagnosis; feature extraction 安徽省高校自然科学研究重点项目(KJ2016A529);滁州学院规划研究项目(2014GH20);滁州学院2016年科研启动基金(2016QD08) 2016-04-01 修改稿收到日期:2016-07-04 王 波 男,讲师,博士,1982年生 TH212; TH213.3 A 10.13465/j.cnki.jvs.2017.05.017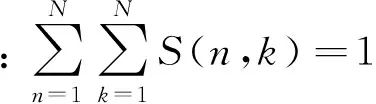
2 基于QGA优化GST的故障特征提取方法描述
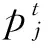
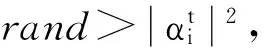
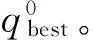
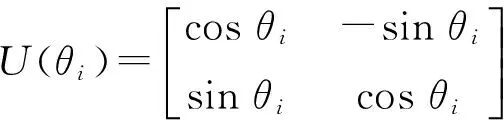
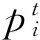
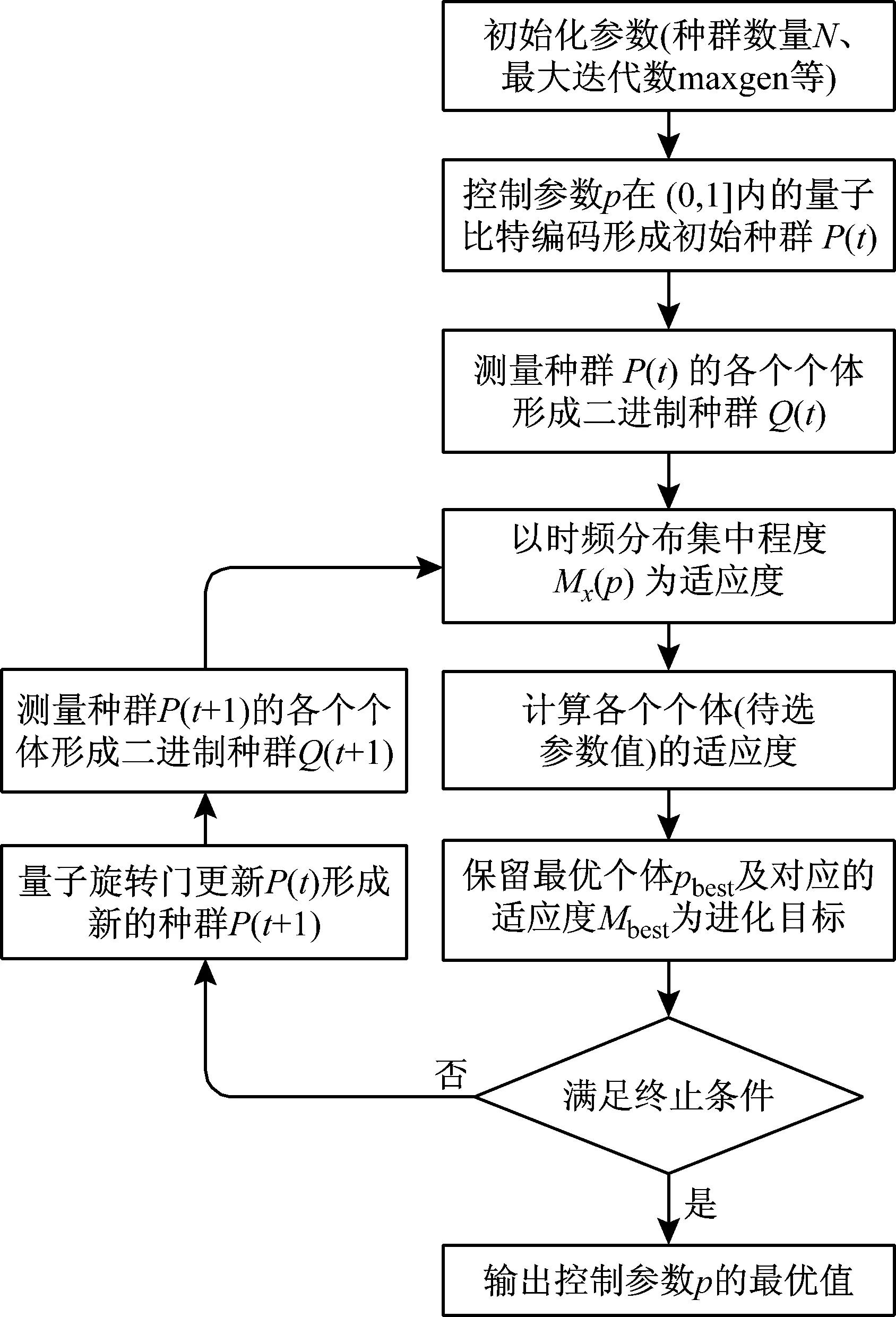
3 滚动轴承故障诊断实例分析
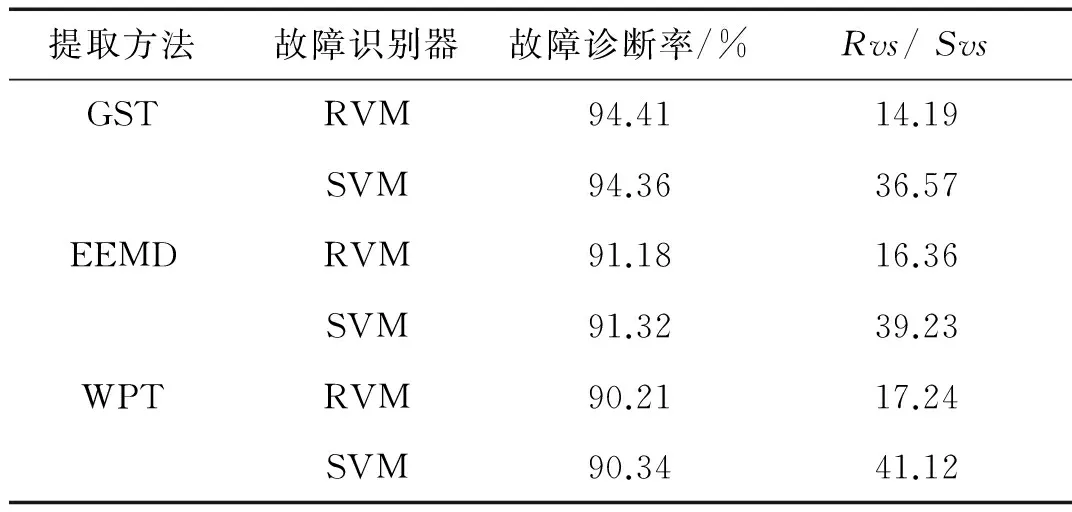
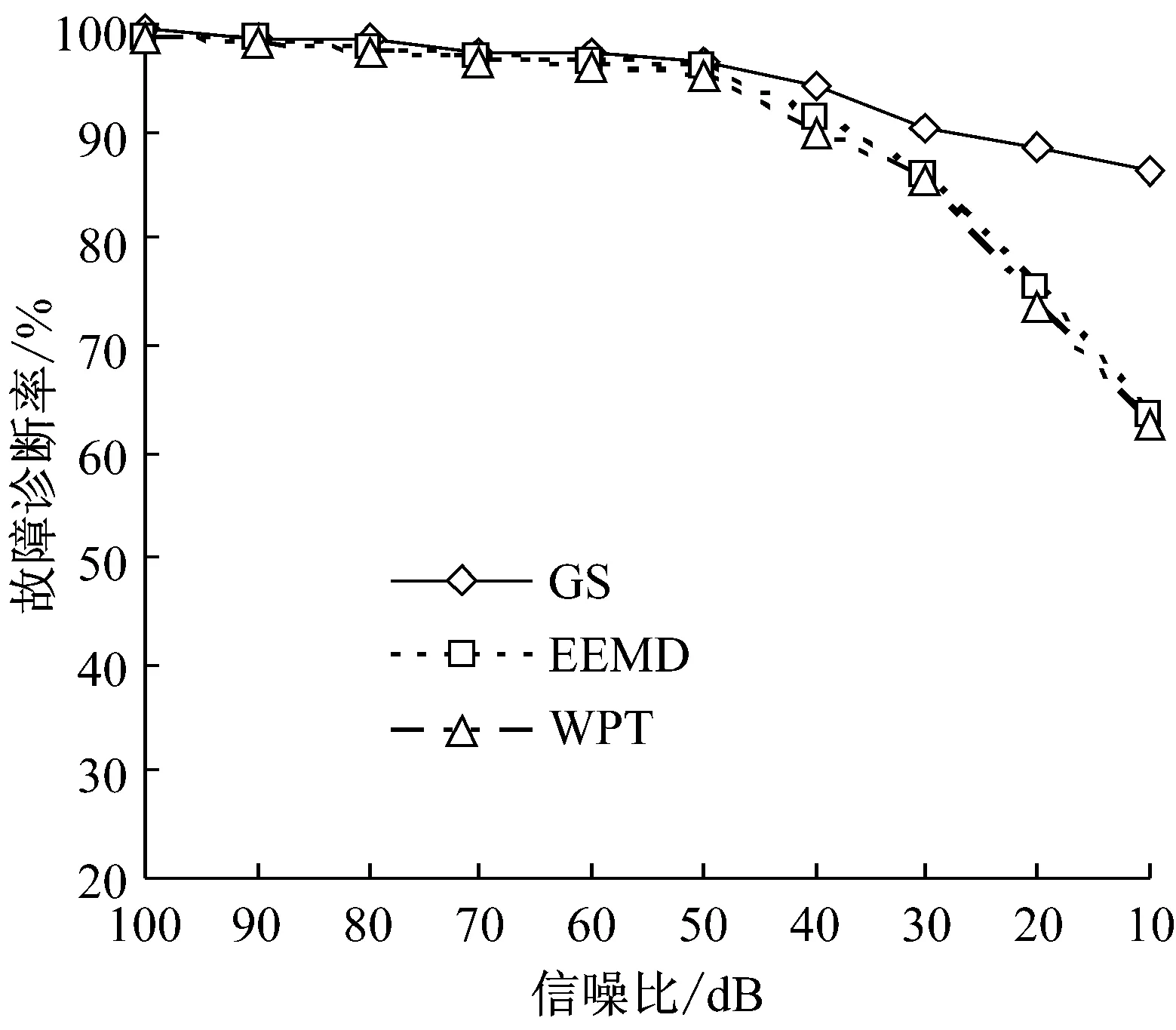
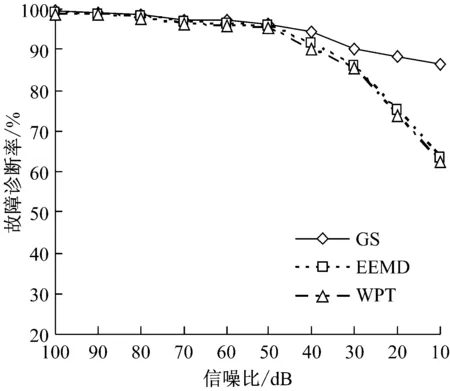
4 结 论
