基于双树复小波降噪和Katz分形维迹线融合的板类结构损伤检测

白润波，徐宗美，张建刚

(1.山东农业大学 水利土木工程学院，山东 泰安 271018； 2.河海大学 力学与材料学院，南京 210098)

基于双树复小波降噪和Katz分形维迹线融合的板类结构损伤检测

白润波1,2，徐宗美1，张建刚1

(1.山东农业大学 水利土木工程学院，山东 泰安 271018； 2.河海大学 力学与材料学院，南京 210098)

目前基于振动响应的板类结构损伤检测技术存在着噪声免疫力弱、对轻微损伤难以识别等困难。对此，提出一种对板振型进行双树复小波变换(DT-CWT)降噪和仿射变换预处理的Katz分形维迹线扫描融合的板结构损伤检测方法。该方法首先利用DT-CWT对原始实测板结构的振型信号进行降噪；然后将降噪后的振型沿板纵、横向离散分解为振型曲线；将分解后的振型曲线进行仿射变换，得到拉伸后的线型面图；对变换后的线型面图分别进行Katz分形维迹线扫描，得到沿板纵向和横向的分形维迹线曲面图，将二者取均值得到融合后的分形维迹线曲面图；此融合后的曲面图中的凸起预示了损伤的发生，凸起的位置、形状和尺寸反应了损伤所在的位置、形状和尺寸。通过两个模型试验证明了该方法对板结构损伤识别的有效性；对比分析说明了对振型进行DT-CWT降噪和仿射变换预处理的重要性。

损伤检测； 板； 双树复小波； 分形维； 仿射变换； 振型

结构健康监测对保障结构物的安全性和正常运行非常重要。目前基于振动理论的结构无损检测是该领域的一个研究热点。它的基本力学原理是：结构动力学参数(固有频率、振型、模态阻尼)是结构物理特性(质量、刚度、阻尼)的函数，损伤所致结构物理特性的改变必然引起结构动力学参数的变化[1]。因而，依据结构动力学参数的改变可以判断结构损伤的发生及状况。与其他振动响应参数相比，振型既是对结构整体力学特征的描述，又包含了结构局部的状态信息，具有实现结构损伤全面深入识别与预警的潜力。目前基于结构振型及其衍生量已产生了很多结构损伤检测方法，如振型曲率法[2]、应变能振型法[3]、振型小波变换系数法[4]、振型分形维迹线法[5]等。这些方法大多针对梁类结构，且普遍存在抗噪能力弱、对轻微损伤不敏感等不足[6-8]，有些方法还需要依赖无损结构模型作参照以映衬损伤[9-10]。实际工程应用中，量测振型信号不可避免含有噪声，且微小损伤引起的振型变化量很小，难以被直接观察到。如何有效去除噪声，并提取出结构损伤奇异信息仍然是亟待解决的一个问题。

本文以工程上广泛应用的板类构件为分析对象，研究建立噪声环境下板类结构损伤识别的有效方法。首先，基于软阈值法，利用双树复小波变换(Dual Tree Complex Wavelet Transform, DT-CWT)对量测振型信号进行降噪；然后将梁的分形维迹线扫描法[11-12]在板上作推广，提出了利用板纵、横向分形维迹线取均值来提取板结构损伤奇异信息的方法。特别的，针对目前分形维迹线扫描法应用于结构高阶振型时，在振型曲率转折处分形维迹线会凸起而淹没损伤导致的凸起的问题[13-14]，提出了基于仿射变换而能克服这一不足的损伤检测方法。模型试验分析表明，本文所提方法对应用高阶振型进行板损伤检测效果良好，能检测出不同的损伤类型、损伤位置及其尺寸大小。

1 DT-CWT阈值降噪

1.1 DT-CWT

实测板构件的振动信号中不可避免含有噪声，噪声的去除是损伤检测技术的一个重要环节。小波变换凭借其良好的时频特性、低熵性和多分辨分析的特点在图像的去噪方面获得了广泛应用。传统的离散小波变换存在着时移敏感性、方向性信息少和缺少相位信息等不足，造成了传统小波在实际应用中存在或多或少的缺陷。1998年，KINGSBURY[15]提出了双树复小波变换(DT-CWT)。DT-CWT采用两个离散小波变换来并行处理输入信号，可以分别得到小波系数的实部和虚部。复小波可以表示为:

(1)

式中：φh(t)、φg(t)分别表示复小波的实部和虚部，它们都是实函数，这样DT-CWT可以表示为两个独立平行的实小波变换。DT-CWT在信号的分解与重构过程中始终保持虚部树的采样位置位于实部树的中间，使之能有效利用实部树和虚部树的小波分解系数，实现实部树和虚部树的信息互补和近似平移不变性，减少了有用信息的丢失。而且，DT-CWT在各层分解过程中利用小波系数二分法减少了多余的计算，提高了计算的速度。

二维DT-CWT可以通过一维双树复小波的张量积得到：

φ(x,y)=φ(x)φ(y)

(2)

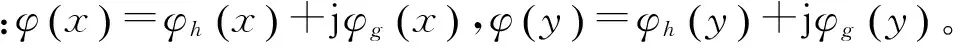
双树复小波变换分解二维信号与离散小波变换类似，利用可分离的滤波器先沿着列再沿着行实现分解。可以得到2个近似(低频)子带和6个细节(高频)子带，后者分别对应于图像中6个不同方向(±15°、±45°、±75°)的信息。

DT-CWT具有的近似平移不变性和良好的方向选择性，以及完全重构性、有限的数据冗余和计算效率高等优点，使其在图像降噪方面拥有巨大的应用潜力。

1.2 阈值降噪

DONOHO等[16]提出了基于小波阈值的去噪方法，该方法在最小均方差意义下可以达到近似最优，能在去除信号噪声的同时，有效保留信号边缘、特征尖峰等信息。阈值降噪的基本原理是：小波变换时把信号的能量集中在一些大的小波系数上，而噪声的能量分布于整个小波域内。所以在信号去噪时认为幅值较大的小波系数是信号的主要成分，而幅值较小的小波系数认为是噪声。于是，采用阈值的办法可以把信号系数保留，而使大部分噪声系数减少至零。

本文基于DT-CWT的阈值降噪操作过程为：对实测板结构振型信号进行DT-CWT分层分解，保留大尺度低频小波系数；对于各尺度高频小波系数，采用软阈值法，即设定一个阈值λ，把绝对值大于λ的小波系数减去λ，把绝对值小于λ的小波系数置为零。最后将处理后获得的小波系数利用逆双树复小波变换进行重构，从而去除实测振型信号中的噪声成分。其中λ可按下式计算[17]

(3)

式中：N为该层小波系数的个数，噪声标准差σ可以用经验公式估计[16]，即

(4)

式中：wj,k为第j层的小波系数。

2 板损伤的分形奇异特征提取

对于结构轻微损伤的情况，即使采用经过降噪后的振型信号，一般来说仍无法直接判定出损伤状况，需要进一步采取提取损伤奇异性的措施。近年来，基于分形理论的结构损伤特征提取方法获得了研究应用。其中基于Katz分形维的梁类结构损伤检测取得了较好的效果，能通过对梁结构的振型进行逐点分形维计算扫描，由分形维迹线上的凸起来判断损伤的发生及确定损伤的位置和尺寸大小[11-14]。本节即采用Katz分形维迹线扫描法，将针对一维梁结构损伤的Katz分形维特征提取方法向二维板结构作推广。

2.1 梁结构损伤的Katz分形维特征提取

考虑具有点序列(s1,s2, …,sN)形式的波形f(s)，N表示序列的点数。这个序列的点可以写成一个二元组：si(xi,yi)，i=1,2,…,N；xi是水平轴上的值，yi是对应xi的竖直轴上的值。对此Katz分形维数可定义为[18-19]：

(5)

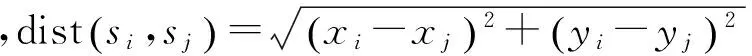
梁结构损伤的Katz分形维特征提取方法为：对梁的振型曲线，首先建立一个含有一定数目样本距离的滑动窗，使滑动窗沿振型曲线不断前移，新的采样点移入窗内，同时上个采样点移出窗外。每次移动滑动窗均按式(5)计算窗内所含曲线段的Katz分形维数，并作为该滑动窗中心样本点的分形维数值。随着滑动窗遍历整条振型曲线，便得到一条相应的振型分形维数迹线。通过此振型分形维数迹线来分析，曲线上凸起的位置即可能的损伤位置。为方便下文引用，将所述这一操作过程记为J。

2.2 板结构损伤的Katz分形维特征提取

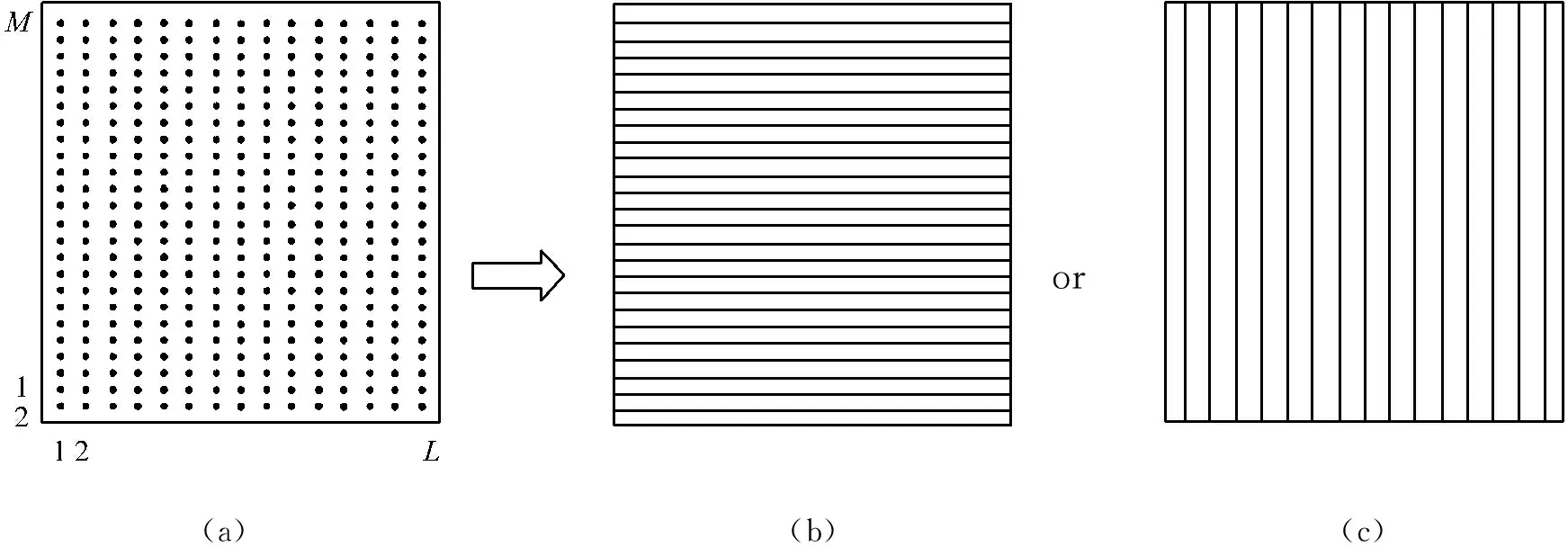
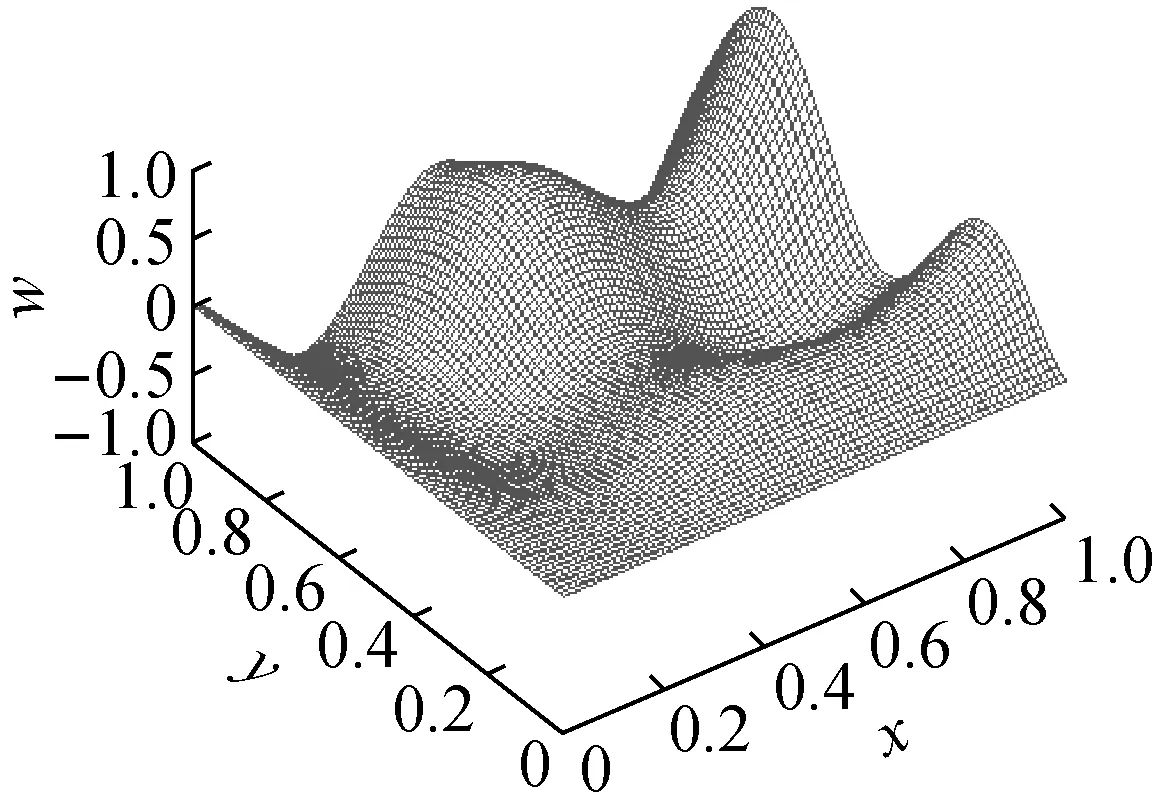
对一含有L×M个测点的板(图1(a))，其二维平面布置可近似看作是由水平向M条一维的线(图1(b))或竖直向L条一维的线((图1(c))构成的二维图。图1(b)与图1(c)的侧重方向不同，是从不同侧面对图1(a)的近似。图2(a)为板的某阶振型图，它可以近似看作是由图2(b)x向曲线构成的曲面图，或由图2(c)y向曲线构成的曲面图，它们与原始由网格点布置形成的曲面图2(a)相比会有一定的差别。若将图2(b)和图2(c)二者取均值融合可在一定程度上消除离散图的方向效应，是对原始图形的良好近似，并能将二维网格图降维为若干一维线型图。基于这一理念，将一维梁结构损伤的Katz分形维特征提取方法向二维板结构作推广。

(a)(b)or(c)

图1 板测点布置及其近似表示

Fig.1 Layout of the measured grid points of a rectangular plate and its approximate expression

(a)

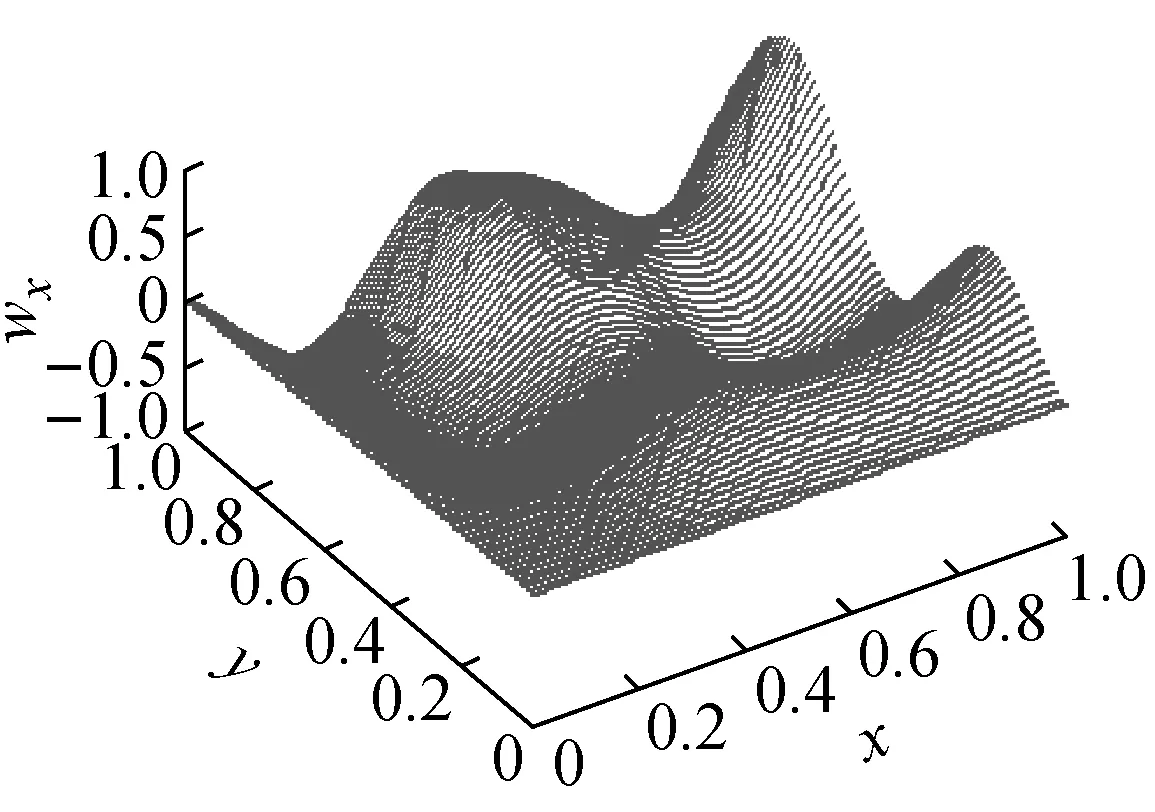
(b)

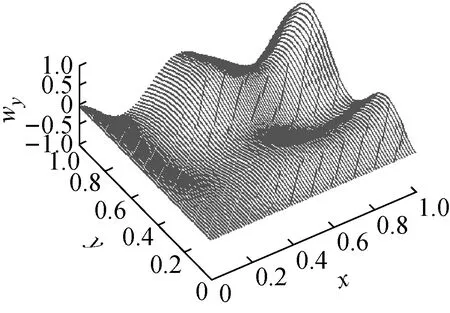
(c)

板结构损伤的Katz分形维特征提取方法采用以下策略：假设板的某阶振型W由L×M个采样点(如图1(a))实测绘成，将W分别离散为由水平向M条波形线和竖直向L条波形线构成的曲面图。进行结构损伤特征提取时，可对沿板水平向的M条波形线分别执行梁结构损伤的Katz分形维特征提取操作J，组成此种情况下的分形维迹线曲面图FDH；类似的，可对沿板竖直向的L条波形线分别执行梁结构损伤的Katz分形维特征提取操作J，组成此种情况下的分形维迹线曲面图FDV。最后，将FDH和FDV取均值融合得到用于板损伤特征提取的分形维迹线曲面图FD。FD图形中发生突变处即可能的损伤位置，凸起的的形状和尺寸反应了损伤的形状和尺寸。公式表示为：

V

FDH(j)=J{W(1：L，j)}，j=1，2，…，M

(6)

FDV(i)=T{W(i，1：M)}，i=1，2，…，L

(7)

FD=(FDH+FDV)/2

(8)

FDH适合检测板上的竖直向损伤，而FDV则适合检测板上的水平向损伤。采用式(8)FDH和FDV两者取均值的融合结果则综合了二者的扫描效应，对水平向、竖直向、斜向裂缝，以及腐蚀、分层及孔洞等损伤均有望有效提取其Katz分形维特征。

特殊的，对异形板，需区分出板的横向和纵向，将横向和纵向进行合理划分，使采样点沿两向都能连续、规整分布；扫描时沿板横向边和纵向边依次顺序进行，并应注意分形维数值与板坐标值之间的对应关系。

3 板损伤识别方法

3.1 高阶振型的仿射变换

很多文献研究表明高阶振型比低阶振型含有更丰富的局部位置信息，对于结构的损伤识别更加灵敏[19-21]。而且随着扫描式激光测振仪等现代量测设备的产生，对某些结构的高阶模态信息已可精确获得。然而，由于高阶振型所含波形数较多，将分形维迹线扫描法应用于高阶振型进行结构损伤检测时，分形维迹线在振型曲率转折处会跳起(伪奇异)，从而与损伤引起的分形维迹线凸起相混淆，导致损伤识别失败[12-14]。本节设计提出仿射变换式用于对板结构振型的预处理，使消除高阶振型上的曲率转折点，从而减弱分形维迹线扫描中的伪奇异现象，达到对板结构进行损伤识别的目的。

对板的模态振型或工作振型(x,y,w)，x,y为板上采样点的坐标值，w为对应采样点的振型幅值，通过式(9)，设计一合适的仿射变换式A，可使结构振型曲线或曲面变得平缓，没有曲率转折点，而原有图形的相对位置关系、线型形式不发生变化。这样有望大幅减弱振型曲率变化引起的分形维迹线的凸起，而只将由损伤引起的分形维迹线凸起显现出来，达到正确判定结构损伤的目的。

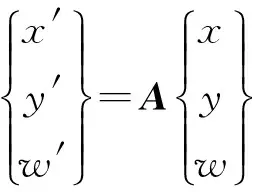
(9)

沿板x向离散分解时，A有如下形式：

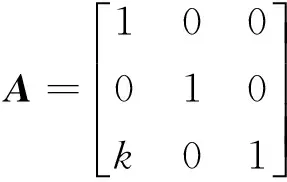
(10)

式中:仿射变换式A包含一拉伸系数k，通常在振型振幅归一化的情形下，k可取为：k≥100/l，l为设定单位下板离散方向的长度数值。k在一个很宽阔的范围内取值均能达到拉伸原始曲线而使其没有曲率转折点的目的。

沿板y向离散分解时，只需将式(10)矩阵第三行的前两列位置对调即可实现同样的目的。

图3(a)、(b)分别为图2(b)、(c)按式(9)取k=100时作仿射变换后的图。由图可见，经仿射变换后，板振型离散分解图上的曲率转折点得以消除，于是可以减小原始曲率转折点附近区域Katz分形维的计算值；相对应的可以凸显损伤引起的分形维值，由此可利用分形维迹线扫描法进行板结构损伤识别。

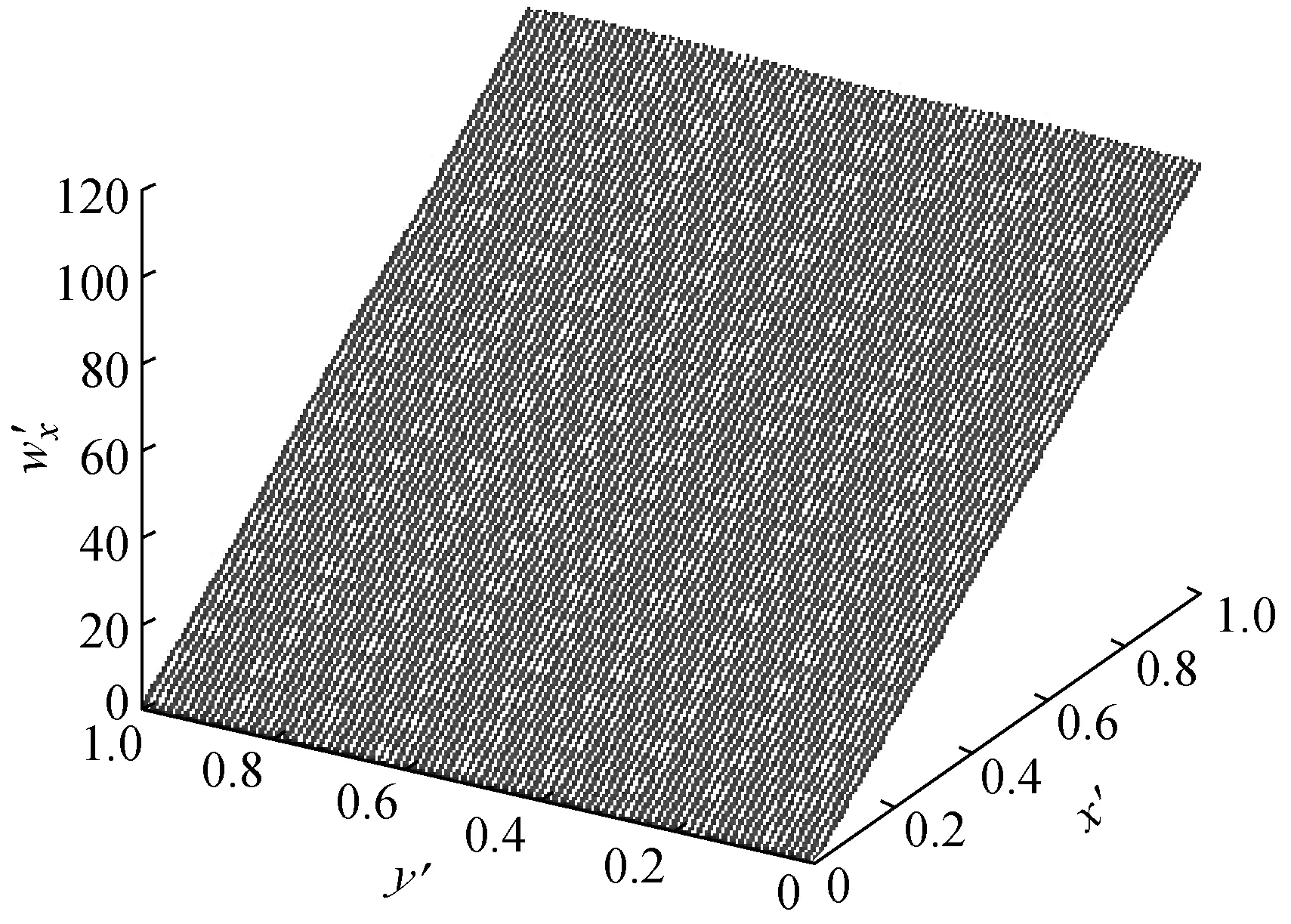
(a)

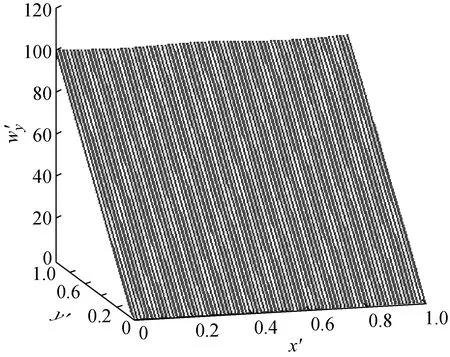
(b)

Fig.3 Vertical and transverse decomposition mode shape lines by the specific affine transformation withk=100

3.2 板损伤识别流程

板类结构损伤识别的流程如图4所示。首先利用DT-CWT将原始实测振型信号进行分层分解，按式(3)计算阈值，根据软阈值法将分解的小波系数处理后进行逆双树复小波变换重构，使实测振型信号得以降噪。然后将降噪后的振型图沿板纵、横向分别进行离散分解，形成如图2(b)、(c)所示形式的振型曲线。将分解后的振型曲线按式(9)进行仿射变换，得到如图3所示形式的没有曲率转折点的线型面图。对变换后的线型面图分别执行式(6)、(7)的Katz分形维迹线扫描操作，得到沿水平向和竖直向的分形维迹线曲面图FDH和FDV。按式(8)将FDH和FDV取均值得到融合后的分形维迹线曲面图FD。根据融合后的FD图，图形中的突变状况预示了结构中的损伤状况，凸起的位置、形状和尺寸表示了损伤所在的位置、形状和尺寸大小。

图4 板结构损伤识别流程图Fig.4 Flow chart of the damage identification for plate-like structures

4 模型试验分析

采用两个模型试验来验证所提方法对板类结构损伤识别的有效性。试验一用于对板上复杂裂缝的检测，试验二用于对复合材料板上局部块状损伤的检测。

4.1 板复杂裂缝检测

4.1.1 试验布置

模型试验一为一方形铝板，铝板上有一用小刀刻划的“X”型交叉缝，裂缝(刻痕)每边长40 mm，宽1 mm，深1 mm。铝板厚度为4 mm，其平面尺寸及裂缝布置如图5所示。采用直径为10 mm的圆形压电陶瓷换能器(Piezoceramic Transducer，PZT)产生谐激励，由扫描式激光测振仪(3D Polytec PSV-400)量测板的振动模态。量测范围为图5中920 mm × 920 mm的灰色区域，共包含451 × 449个均匀布置的采样点。以试验测得的829 Hz激励下的振型(图6)为例，采用本文方法进行结构损伤检测。

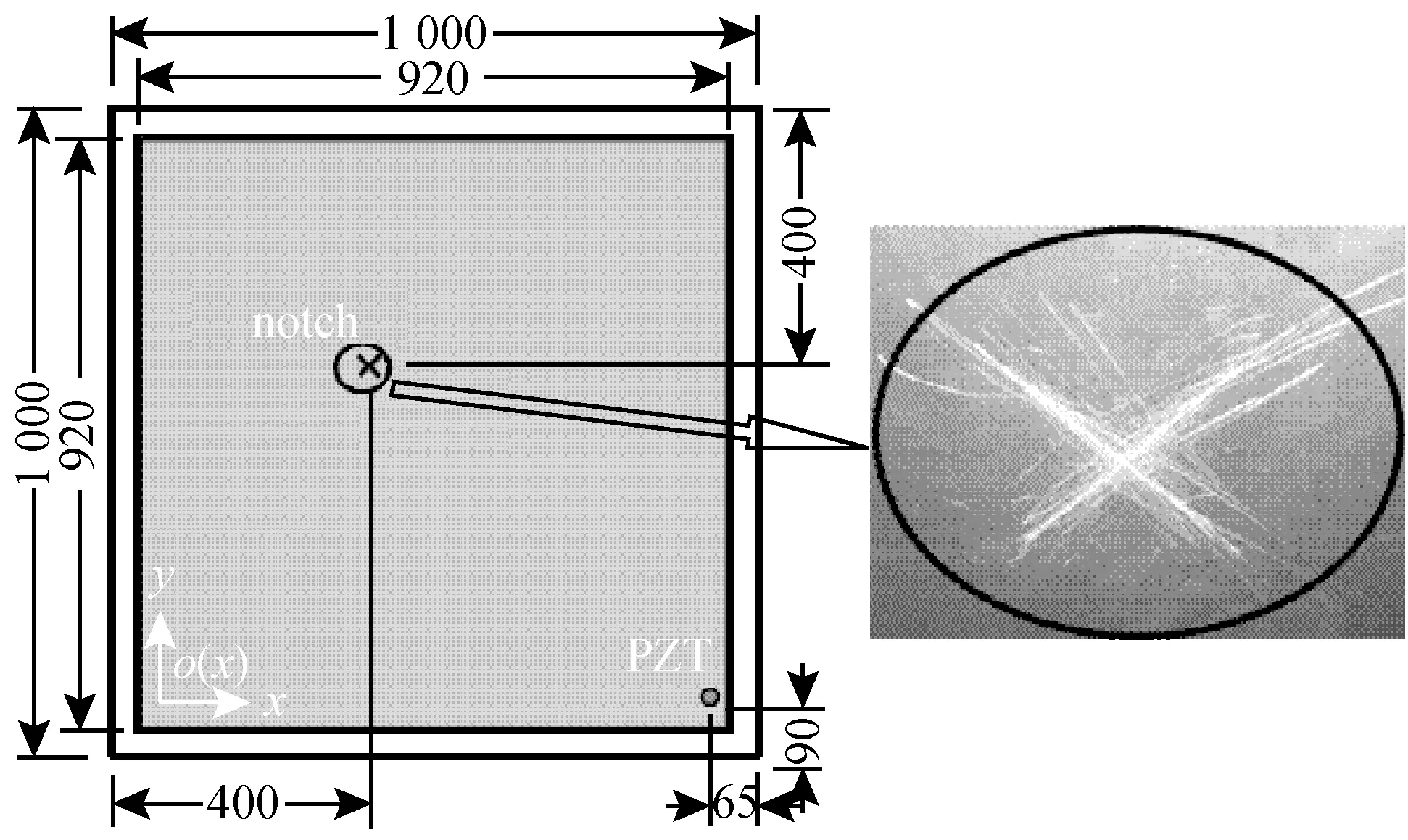
图5 铝板平面尺寸及裂缝布置图(mm)Fig.5 Geometry of the aluminum plate with a cross-like notch (mm)

4.1.2 裂缝损伤检测

首先利用DT-CWT对829 Hz激励下板的振型作降噪处理，这里分解为4层，降噪处理后的振型如图7所示。将降噪后的振型沿板纵、横向离散分解成振型曲线；板的尺寸单位取mm，将离散的振型曲线按式(9)进行仿射变换，板纵、横向仿射变换式中k均取为0.1(0.1=100/1 000)。对仿射变换后的线型面图分别执行Katz分形维迹线扫描操作，并将得到的FDH和FDV取均值得到融合后的分形维迹线曲面图FD。需要说明的是，为方便图形标注，这里将融合后图的纵坐标取对数表示，即所有纵坐标显示为log10(FD)，最后形成如图8所示的损伤检测图。图8(a)中分形维数值大处对应的凸起部分预示着该处可能存在损伤，凸起部分在图8(b)平面图上对应着色彩亮度高的区域，清晰地显示了损伤的位置和“X”的裂缝形式，这与试验一预设的损伤位置、形式和尺寸相吻合。

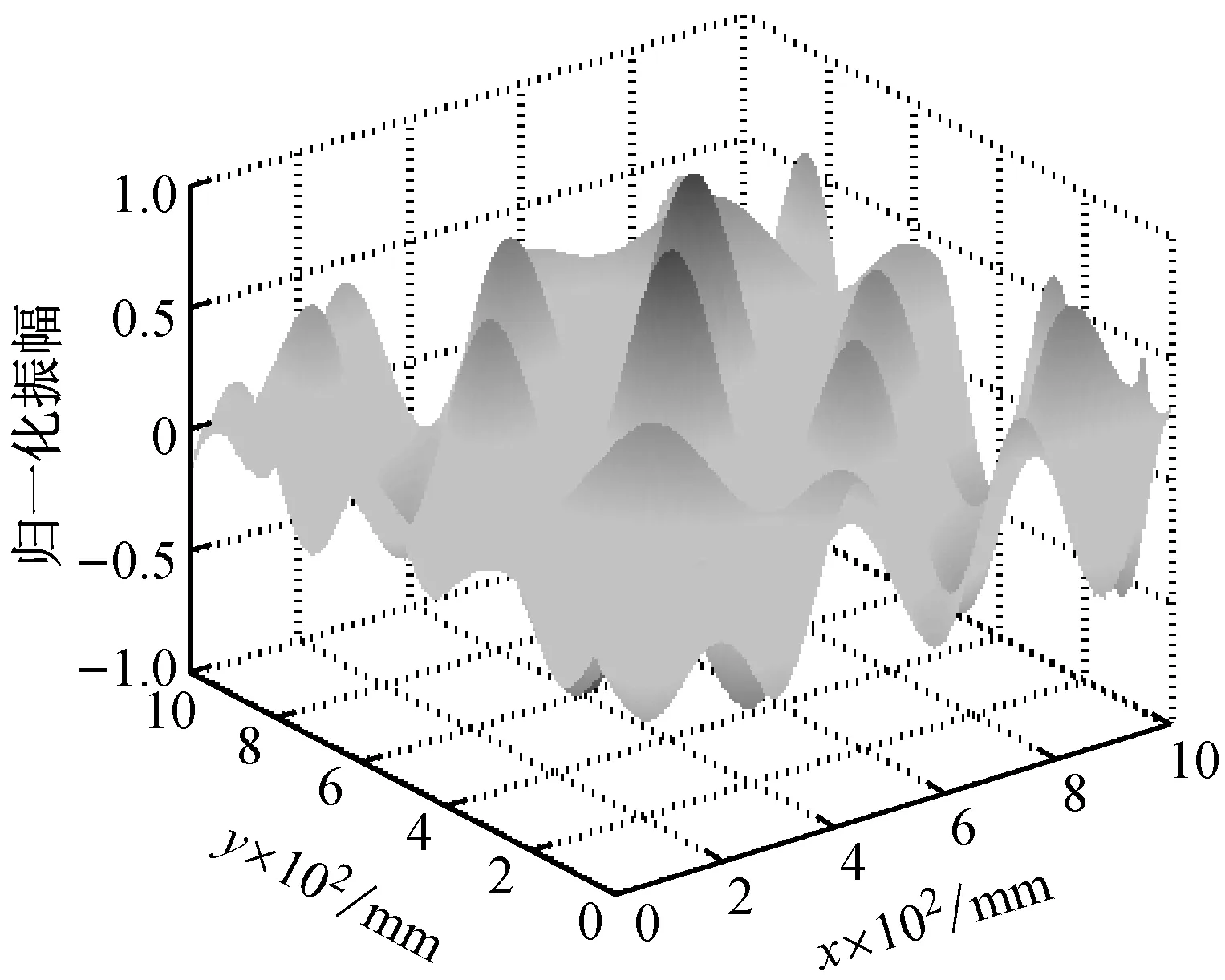
图6 试验一829 Hz激励下的板振型图Fig.6 Mode shape at excitation of 829 Hz for the cracked aluminum plate

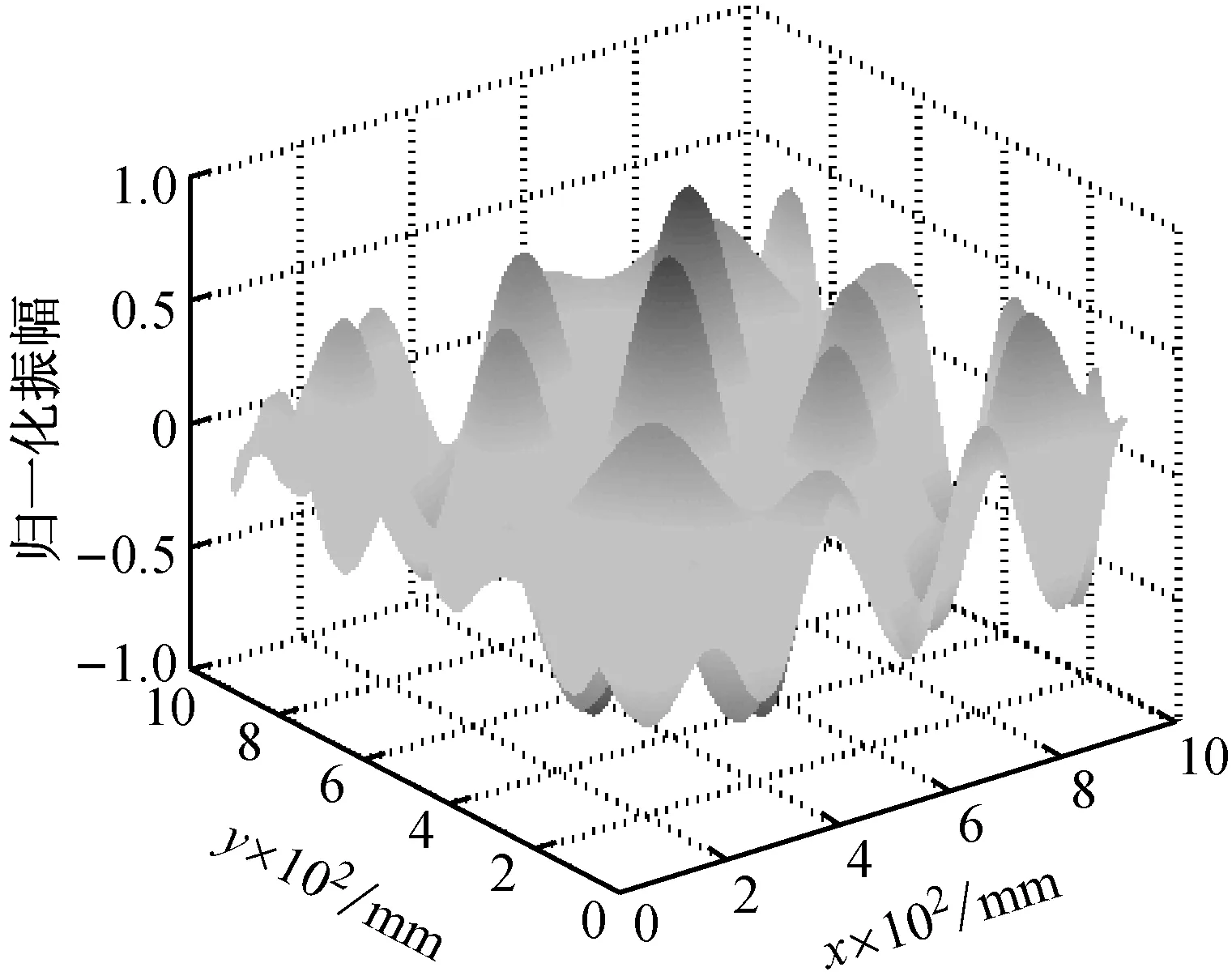
图7 试验一829 Hz激励下DT-CWT降噪后板振型图

Fig.7 Mode shape at excitation of 829 Hz after denoising by DT-CWT for the cracked aluminum plate

4.1.3 对比分析

为分别说明本文方法中对量测振型进行DT-CWT降噪和仿射变换预处理的作用，作了如下两个对比分析。

对未经DT-CWT降噪的原始量测振型(图6)执行上述振型离散、仿射变换、Katz分形维迹线扫描操作，并将得到的FDH和FDV取均值得到融合后的分形维迹线曲面图lg10(FD)，如图9所示。很明显，由于噪声的干扰，图9显示为很多无规则的凸起，损伤信息被噪声所掩盖，无法识别出板上的裂缝损伤。

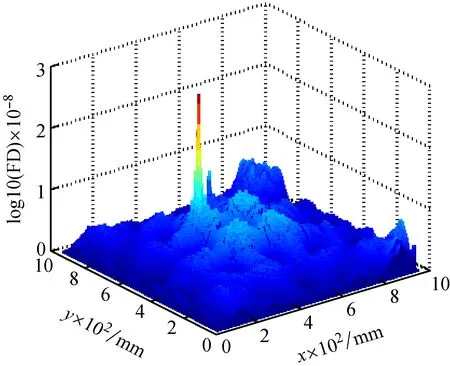
(a) log10(FD)立体图

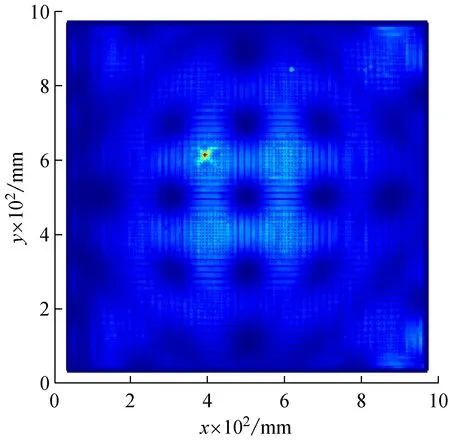
(b) log10(FD)平面图

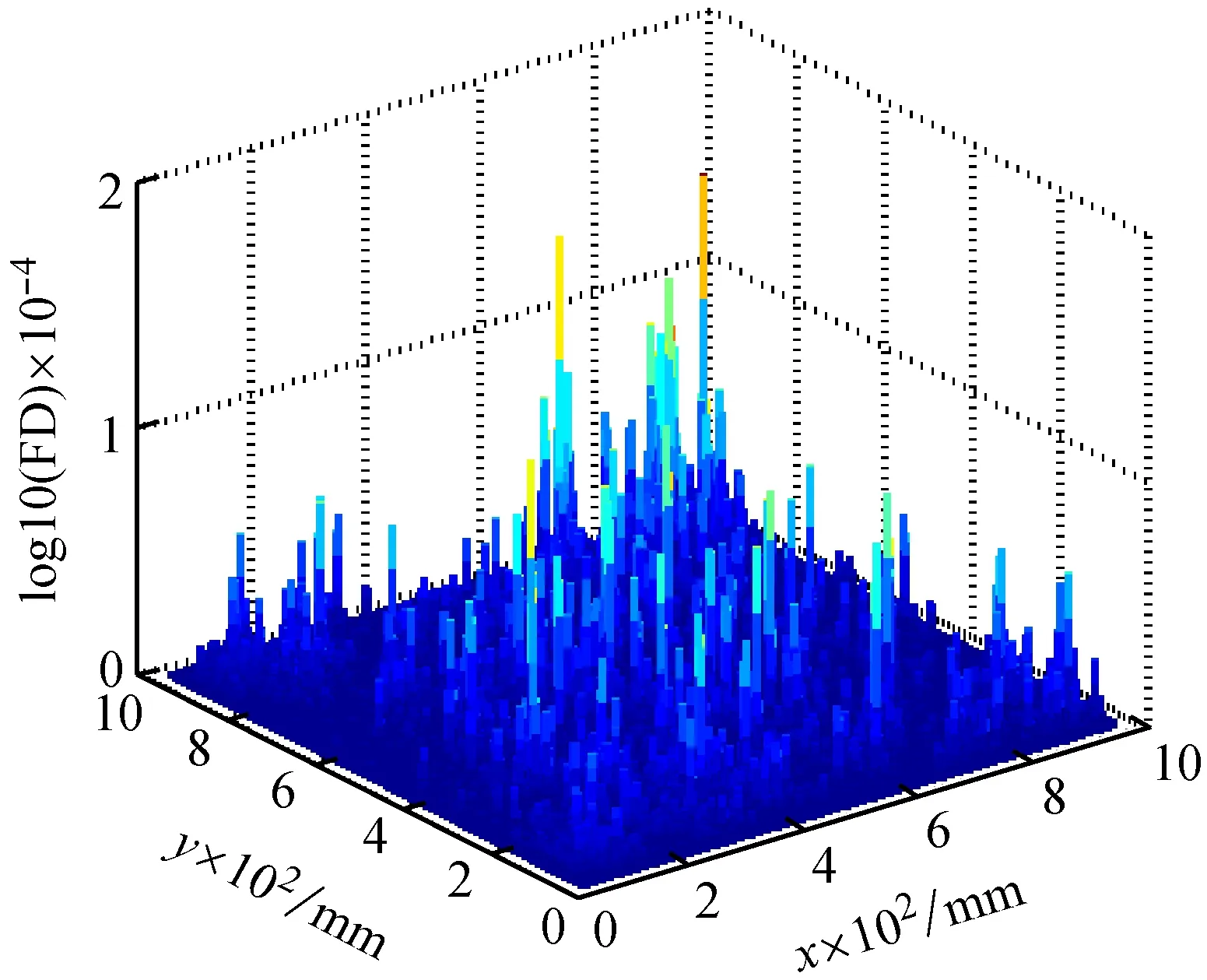
(a) log10(FD)立体图

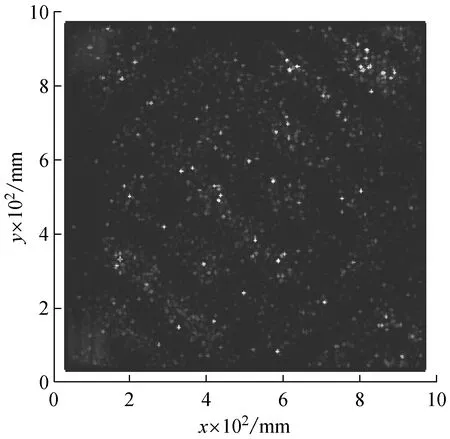
(b) log10(FD)平面图

对经DT-CWT降噪后的振型(图7)不进行仿射变换预处理，而直接离散分解后执行Katz分形维迹线扫描操作，将得到的FDH和FDV取均值得到融合后的分形维迹线曲面图log10(FD)，如图10所示。由图10可见，由于振型图波形数较多，在振型曲率转折处log10(FD)迹线图中相应有较多凸起，这些凸起与由损伤引起的凸起混叠在一起，致使无法准确识别出损伤。

4.2 复合材料板局部块状损伤检测

4.2.1 试验布置

试验二采用一方形玻璃纤维增强塑料(Glass Fiber Reinforced Polymer, GFRP)压层板，GFRP板厚度为2 mm，厚度方向上由四层等厚单向排列的玻璃纤维毡组成。在压层板局部挖除一层玻璃纤维毡，大小为长×宽×厚=20 mm×20 mm×0.5 mm，压层板平面尺寸及损伤布置如图11所示。在板中心位置布置一直径为10 mm的圆形压电陶瓷换能器(PZT)，使之产生谐激励，由扫描式激光测振仪(3D Polytec PSV-400)量测板的振动模态，共包含271×271个均匀布置的采样点。以试验测得的388 Hz激励下的振型(图12)为例，采用本文方法进行损伤检测。

4.2.2 局部块状损伤检测

基于388 Hz激励下板的振型，按照图4所示结构损伤识别流程得到如图13所示的分形维迹线曲面图log10(FD)。图13(a)中分形维数值大处对应的凸起部分预示着该处可能存在损伤，凸起部分在图13(b)平面图上对应着色彩亮度高的区域，清晰地显示了损伤的位置、形状和大小，这与试验二预设的损伤位置、形状和尺寸相吻合。

(a) log10(FD)立体图

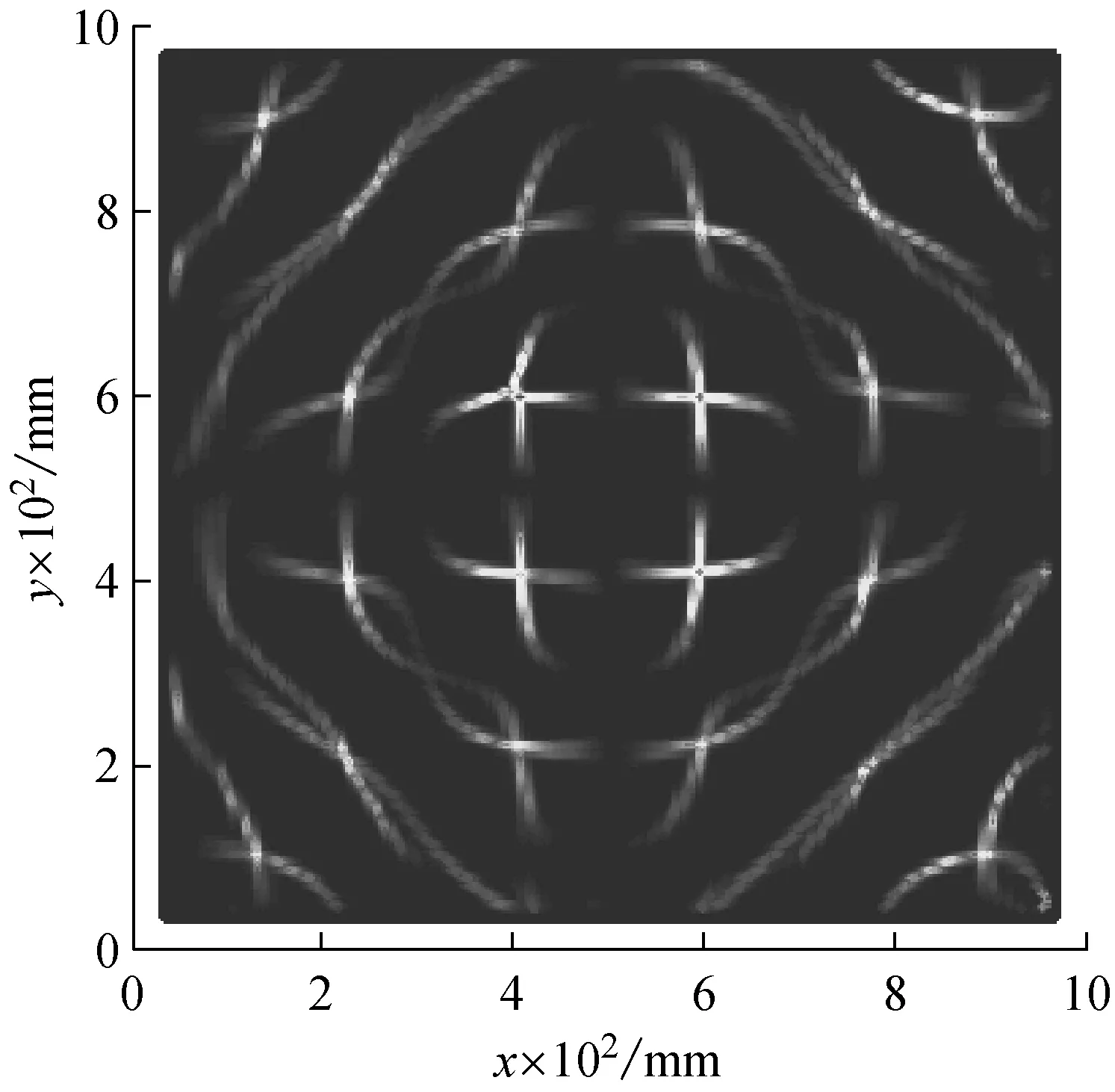
(b) log10(FD)平面图

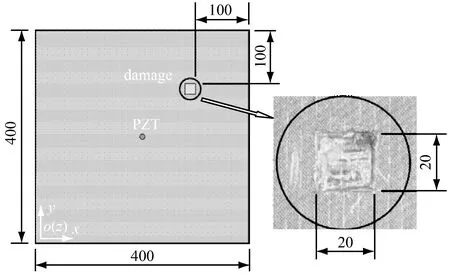
图11 GFRP板平面尺寸及损伤布置图(mm)Fig.11 Geometry of the GFRP plate with a local square damage.(mm)

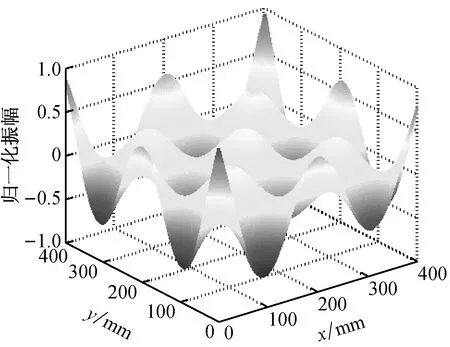
图12 试验二388 Hz激励下的板振型图Fig.12 Mode shape at excitation of 388 Hz for the GFRP plate

(a) log10(FD)立体图

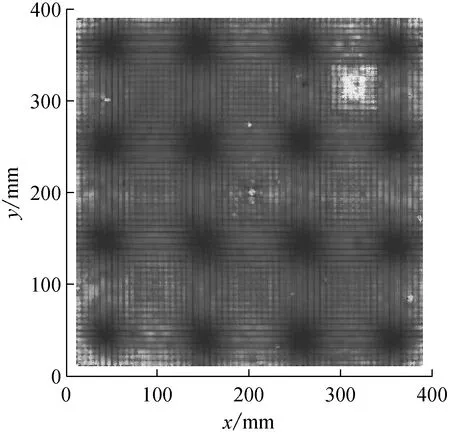
(b) log10(FD)平面图

4.2.3 对比分析

对试验二模型也作了两个对比分析。对未经DT-CWT降噪的原始量测振型执行振型离散、仿射变换、Katz分形维迹线扫描融合操作，得到图14所示的log10(FD)图。与试验一模型的分析结果类似，图14也显示为很多无规则的凸起，损伤信息被噪声所掩盖，无法识别出板上的损伤。

将经DT-CWT降噪后的振型不进行仿射变换预处理，而直接离散分解后执行Katz分形维迹线扫描操作，得到图15所示的融合后的分形维迹线曲面图log10(FD)。由图15可见，在振型的曲率转折处log10(FD)迹线图中相应有较多凸起，不利于损伤信息的正确识别。

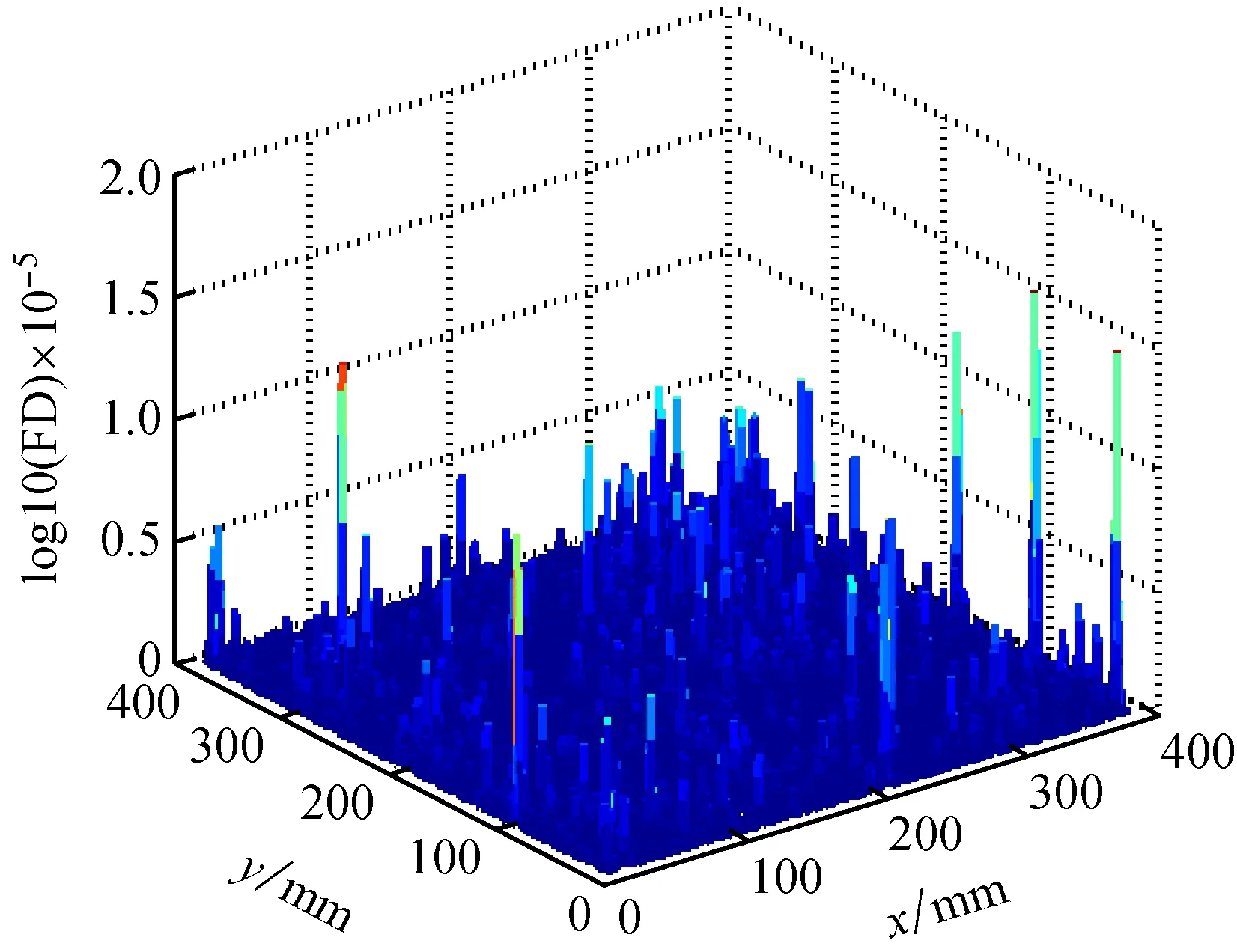
图14 试验二未经降噪处理的损伤检测图Fig.14 Identification of damage for the GFRP plate without denoising

这些对比分析，说明对量测振型进行DT-CWT降噪和仿射变换预处理在板结构Katz分形维迹线扫描法识别损伤中起着重要作用。

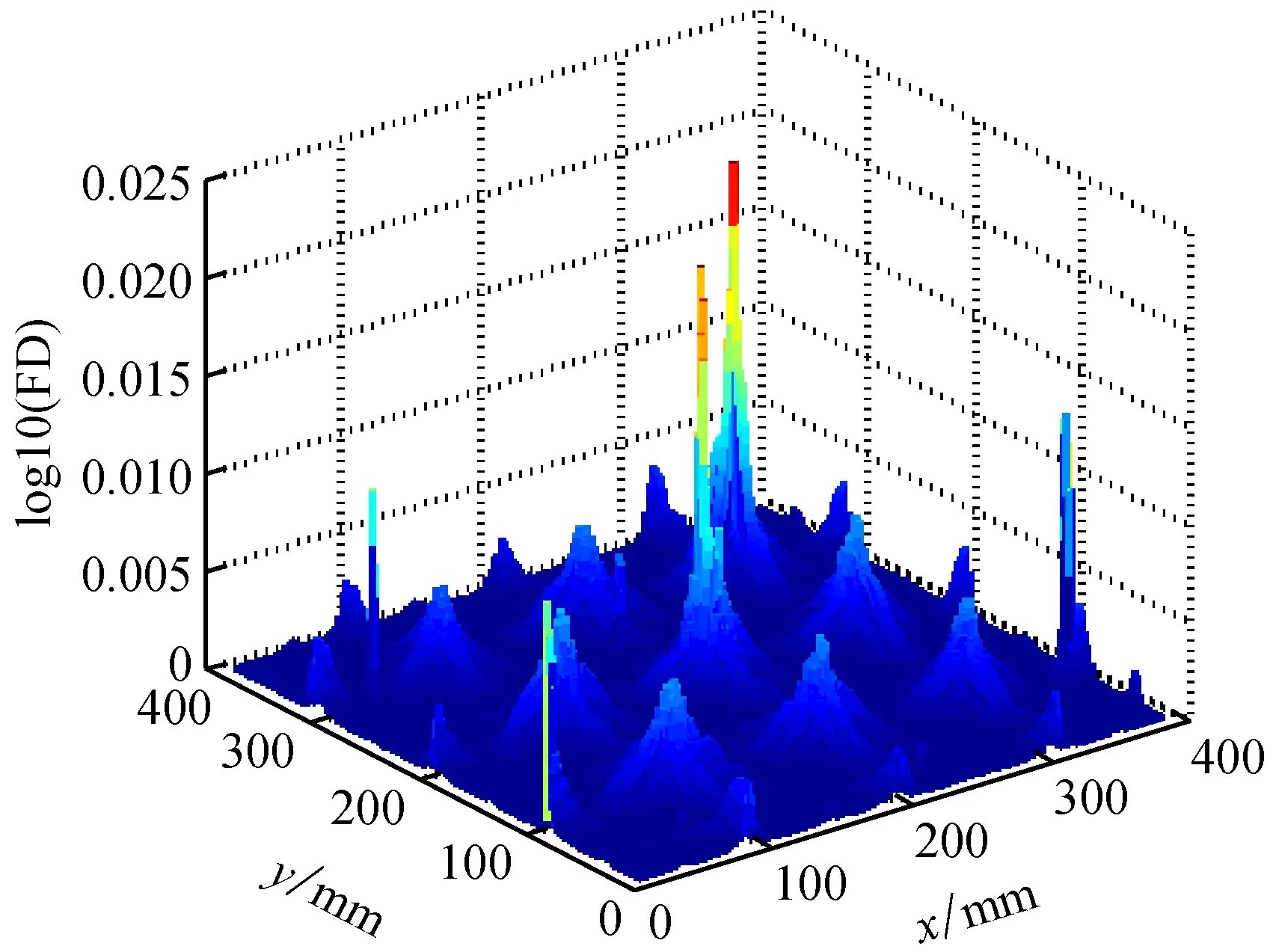
图15 试验二未经仿射变换处理的损伤检测图Fig.15 Identification of damage for the GFRP plate without affine transformation

5 结 语

在对板结构实测模态振型进行DT-CWT降噪的基础上，提出了对板振型进行离散分解并作仿射变换预处理的Katz分形维迹线扫描融合的板结构损伤识别方法。融合后的分形维迹线图中的突变预示着结构损伤的发生，凸起的位置、形状和尺寸对应着损伤发生的位置、形状和尺寸。通过对两个模型试验的分析表明，本文所提方法具有不依赖于无损基准结构模型、能有效利用结构的高阶振型、抗噪能力强、对局部轻微损伤敏感等优点；对板结构上的裂缝、分层等损伤均有良好的识别效果。对比分析说明了对振型进行DT-CWT降噪和仿射变换预处理在本文的损伤识别方法中起着重要的作用。

[1] 朱宏平，余璟，张俊兵.结构损伤动力检测与健康监测研究现状与展望[J].工程力学，2011，28(2)：1-11.

ZHU Hongping,YU Jing,ZHANG Junbing.A summary review and advantages on vibration-based damage identification methods in structural health monitoring[J].Engineering Mechanics,2011,28(2):1-11.

[2] DESSI D,CAMERLENGO G.Damage identification techniques via modal curvature analysis:Overview and comparison[J].Mechanical Systems and Signal Processing,2015,52:181-205.

[3] 姜绍飞，张永强，吴兆旗.基于一阶振型的海洋平台二阶段损伤定位方法[J].华中科技大学学报(城市科学版)，2008,25(3)：31-34.

JIANG Shaofei,ZHANG Yongqiang,WU Zhaoqi.A two-stage damage localization method based on the first mode shape of offshore platform structure[J].Journal of Huazhong University of Science and Technology (Urban Science Edition),2008,25(3)：31-34.

[4] HUDA F,KAJIWARA I,HOSOYA N.Damage detection in membrane structures using non-contact laser excitation and wavelet transformation[J].Journal of Sound and Vibration,2014,333(16):3609-3624.

[5] BAI R B,OSTACHOWICZ W,RADZIEN SKI M,et al.Vibrational damage detection using fractal surface singularities with noncontact laser measurement[J].Journal of Vibration and Control,2014,1077546314548088.

[6] 赵玲，李爱群.基于模态柔度矩阵变化指标的结构损伤预警方法[J].东南大学学报(自然科学版),2009,39(5):1049-1053.

ZHAO Ling,LI Aiqun.Method of structural damage prewarning based on modal flexibility change index[J].Journal of Southeast University (Natural Science Edition),2009,39(5):1049-1053.

[7] NANDA B,MAITY D,MAITI D K.Damage assessment from curvature mode shape using unified particle swarm optimization[J].Structural Engineering and Mechanics,2014,52(2):307-322.

[8] BAI R B,OSTACHOWICZ W,CAO M S,et al.Crack detection in beams in noisy conditions using scale fractal dimension analysis of mode shapes[J].Smart Materials and Structures,2014,23(6):065014.

[9] 黄双杰，徐守彬，刘馨燕.关联维数在梁式结构损伤检测中的应用[J].后勤工程学院学报，2011，27(2):26-29.

HUANG Shuangjie,XU Shoubin,LIU Xinyan.Application of correlation dimension in damage detection for beam structure[J].Journal of Logistical Engineering University,2011,27(2):26-29.

[10] SUNG S H,KOO K Y,JUNG H J.Modal flexibility-based damage detection of cantilever beam-type structures using baseline modification[J].Journal of Sound and Vibration,2014,333(18):4123-4138.

[11] HADJILEONTIADIS L J, DOUKA E, TROCHIDIS A.Fractal dimension analysis for crack identification in beam structures[J].Mechanical Systems and Signal Processing, 2005, 19: 659-674.

[13] BAI R B, CAO M S, SU Z, et al.Fractal dimension analysis of higher-order mode shapes for damage identification of beam structures[J].Mathematical Problems in Engineering, 2012, 2012, 454568.

[14] QIAO P, CAO M S.Waveform fractal dimension for mode shape-based damage identification of beam-type structures[J].International Journal of Solids and Structures, 2008, 45(22/23): 5946-5961.

[15] KINGSBURY N G.The dual-tree complex wavelet transform: a new technique for shift invariance and directional filters[J].IEEE Digital Signal Processing Workshop, 1998, 98(1): 2-5.

[16] DONHO D L, JOHNSTONE I M.Ideal spatial adaptation via wavelet shrinkage[J].Biometrika, 1994, 81(3)：425-455.

[17] DONOHO D L.De-noising by soft-thresholding[J].IEEE Transactions on Information Theory, 1995, 41 (3): 613-627.

[18] KATZ M J.Fractals and the analysis of waveforms[J].Computers in Biology and Medicine, 1988, 18(3): 145-156.

[20] RUCKA M.Damage detection in beams using wavelet transform on higher vibration modes[J].Journal of Theoretical and Applied Mechanics, 2011, 49(2): 399-417.

[21] CAO M S, XU H, BAI R B, et al.Damage characterization in plates using singularity of scale mode shapes[J].Applied Physics Letters, 2015, 106, 121906.

Damage detection for plate-like structures based on DT-CWT denoising and fusion of Katz’s fractal dimension trajectories

BAI Runbo1,2, XU Zongmei1, ZHANG Jiangang1

(1.Shandong Agricultural University, Taian 271018, China; 2.Hohai University, Nanjing 210098, China)

The existing vibration-based damage detection methods are commonly suffered from several limitations, such as, low immunity to noises and insensitivity to weak damages.To solve these problems, here a novel damage detection method was developed for plate-like structures using Katz’s fractal dimension sweep trace technique based on denoising with the dual-tree complex wavelet transformation (DT-CWT) and the affine transformation pretreatment.Firstly, the DT-CWT was used to denoise a original measured vibration signal, the denoised vibration signal was then decomposed into a set of modal shape curves in aplate’s vertical and horizontal directions.The decomposed modal shape corves were then transformed with affine transformation with affine transformation to make the lines no curvature turning point.Secondly, the fractal dimension scanning was applied to the transformed lines to form vertical and horizontal fractal dimension trace surfaces.Finally, the fused fractal dimension trace surface obtained by averaging vertical and horizontal ones was formed for the damage detection.The location and sizes of the damage were determined with the location and sizes of the sudden changes in the fused fractal dimension trace surface.The effectiveness of the proposed method and the importance of the DT-CWT denoising and the affine transformation pretreatment were demonstrated with two model tests.

damage detection; plate; DT-CWT; fractal dimension; affine transformation; modal shape

国家自然科学基金(51508156); 中国博士后科学基金(2014M560386); 山东省自然科学基金(ZR2014EL034)

2015-10-08 修改稿收到日期：2016-02-20

白润波 男，博士后,副教授，1982年4月生

TU311

A

10.13465/j.cnki.jvs.2017.05.014