基于反馈控制的桥梁节段模型干风洞实验仿真

邓 智，宋汉文

(同济大学 航空航天与力学学院，上海 200092)

基于反馈控制的桥梁节段模型干风洞实验仿真

邓 智，宋汉文

(同济大学 航空航天与力学学院，上海 200092)

在风场作用中，针对桥梁结构与风荷载耦合而表现出非自伴随动力系统的现象，提出了仅具有5个独立控制参数的桥梁节段主动控制模型来模拟含有8个颤振气动导数的节段风洞试验模型。该模型由刚体所受的分布力系可等效为集中力系原则出发，利用PID反馈控制技术所构造，其在数学力学模型方面与风洞试验模型完全一致。通过几何变换，干风洞实验测量的线位移信号可转换为角位移信号。同时，运用MIMO分析技术可简单而精确获取系统完备的频响函数矩阵，再采用基于复模态理论中左右特征向量的辨识算法识别控制参数。通过数值仿真，验证了主动控制模型的合理性，同时也显示了该模型在桥梁风振研究中的应用价值和推广意义。

桥梁风振； 主动控制； 模态分析； 参数辨识

风对桥梁的作用由于瞬时空气动力与桥梁风振响应之间存在相位差，使得桥梁有可能从风场中吸取能量而使振幅增大，从而发生颤振。颤振会导致灾难性破坏，1940年美国塔科马大桥因颤振而坍塌就是一个经典实例。因此，颤振分析是现代大跨度桥梁抗风研究的主要内容之一。针对作用在非流线型钝体上的小振幅条件下的非定常气动力，SCANLAN等[1]提出了由颤振气动导数描述的自激励颤振模型，后又提出了二维桥梁断面的颤振气动导数分状态自由振动辨识方法，从而奠定了桥梁气动弹性研究的理论基础。风洞模型试验是获取颤振气动导数的重要手段，主要的试验方法有强迫振动法和自由振动法——强迫振动法在较低、较高风速下都能获取稳定的颤振气动导数，但其试验装置较复杂，试验条件要求和费用较高；自由振动法不适合较高风速及运动响应幅值较大的情况下颤振气动导数的辨识，且试验量和试验难度都较大。

SARKAR[2]提出的基于时域振动模态参数辨识理论的MITD方法，将均匀流和紊流中的气动导数辨识纳入到统一的数学模型，整体辨识所有气动导数。此后，基于现代参数辨识理论的颤振气动导数的整体辨识技术成为桥梁抗风研究领域的一个重要课题。GU等[3-4]采用基于自由振动响应的总体最小二乘(ULS)方法，并通过增加模型惯性量成功实现了节段模型在较高风速作用下颤振气动导数的辨识。BROWNJOHN等[5]运用协方差块Hankel矩阵法来处理节段模型风洞试验的二自由度振动衰减响应，通过系统辨识来提取桥梁节段的颤振气动导数。CHEN等[6]以及CHOWDHURY等[7]分别运用广义最小二乘(GLS)理论以及最小二乘迭代(ILS)方法整体辨识了三自由度节段模型的颤振气动导数。关于桥梁颤振气动导数的辨识理论研究已趋成熟，取得了丰硕的成果[8-11]。受到航空领域地面颤振模拟实验[12]的启示，从振动控制理论出发，本文提出了一种基于主动控制的桥梁节段干风洞(Dry Wind Tunnel)实验模型。以此模型来模拟桥梁节段在风洞模型试验中的动力学特性；然后采用MIMO分析技术，将外激励施加于实际测点而非虚拟测点，进而得到完备的频响函数矩阵；最后采用了ZHANG等[13]提出的一种基于复模态理论中完备左、右特征向量的算法，整体辨识八个颤振气动导数修正量，再经矩阵运算求得系统的反馈控制参数。

1 桥梁节段风洞试验模型自激励模型

桥梁节段在风洞模型试验中简化为二自由度动力学方程：

(1)

(2)

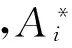
(3)

综合(2)和(3)可得：

(4)

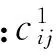
2 干风洞试验思路

2.1 干风洞概念

干风洞包含数据采集系统和反馈控制系统两部分(见图1)。数据采集系统：通过位移或速度传感器采集得到响应信号，记录并整理。反馈控制系统：以数据采集系统的结果作为输入，经过运算得到实时的反馈作用力，并通过激振器作用于桥梁节段。由上述过程建立的试验系统，称之为干风洞。

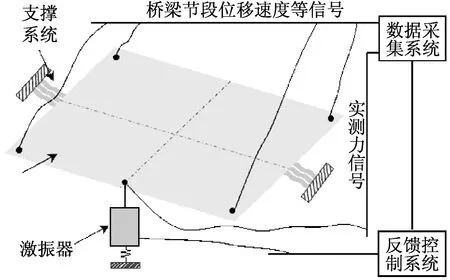
图1 干风洞示意图Fig.1 DWT diagram

2.2 桥梁节段主动控制模型自激励模型

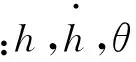
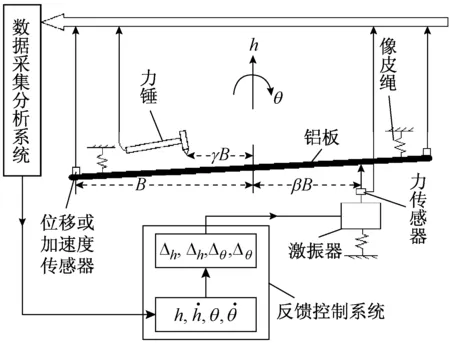
图2 主动控制模型的实验示意图Fig.2 Active control model experiment diagram

(5)

由此可看出，主动控制模型和风洞试验模型具有完全一致的数学模型和力学模型。

如同式(3)此处将自激力写为由反馈控制参数表达的矩阵方程：

(6)

综合和可得：

(7)

至此，原本桥梁节段风洞试验模型需要8个参数来表示，现在主动控制模型中只需5个控制参数。同时也说明，主动控制模型不仅能够完全模拟或替代风洞试验模型，而且还能缩减系统独立参数的个数。

用主动控制模型中的5个控制参数表示8个颤振气动导数：

(8)

由式(8)可以看出，颤振气动导数成对出现且由含有反馈气动中心的等式相互关联。因此，只需5个独立的控制参数即可定义桥梁与风场的耦合作用效果。

2.3 主动控制模型的动力学建模

进一步将桥梁节段模型的动力学方程简化为

(9)

简记为

(10)

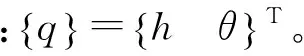
由于流体激振原理或反馈控制作用，桥梁系统的物理结构发生变化，式(10)所述的阻尼、刚度矩阵不再具有对称形式，不再遵守Maxwell互易律，形成非经典系统。尽管有非对称存在，但系统并未同时出现非线性，故叠加原理依然适用。

为方便方程解耦求解，引入几何变换，用沿主动控制模型宽度方向两端的法向线位移来表示系统的竖向位移h和扭转位移θ。假设沿主动控制模型宽度方向两端点的法向响应分别为x1和x2，偏心距都为B，则有如下几何变换：

(11)

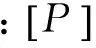
(12)

3 控制参数辨识

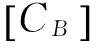
3.1 实验获取频响函数

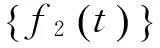
(13)

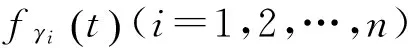
由式外激励产生的响应为

(14)

式(12)的频域形式经整理可得第i次试验中有下面关系：

(15)

式(13)和式(14)频域化处理后，将结果代入式(15)中，并将频域方程扩展得：

(16)

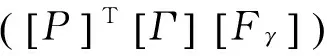
(17)

将各矩阵的具体形式代入式(17)并取数学期望得：

(18)

由上述过程可求得精确的频响函数矩阵。

3.2 左右特征向量辨识算法

又频响函数的具体形式：

(19)

式中：φik,ψjk为系统左右特征向量的元素。

相应地，将频响函数的留数写作向量形式：

(20)

做如下的分解，将得到以矩阵的第一行做归一化的状态空间特征向量矩阵。

(21)

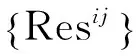
(22)

(23)

计算式(22)的非对角元素,可得:

(24)

则，

(25)

同理,计算式的非对角元素,可得:

(26)

则，

(27)

从式(25)和式(27)可以看出，阻尼阵和刚度阵是独立计算而得的，故数值奇异性不会相互叠加，这也保证了辨识结果的精度。

3.3 求取控制参数

(28)

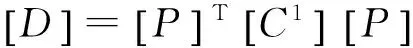
(29)

(30)

又有

(31)

以及

(32)

经过计算即可得到系统的控制参数如下：

(33)

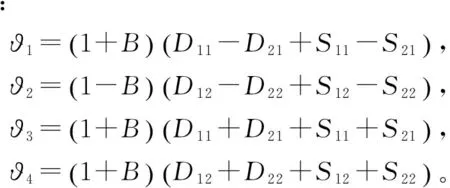
至此，桥梁节段主动控制模型的控制参数已全部通过辨识得到。

4 数值仿真

4.1 数据设定

参考[14]设定主动控制模型自身结构参数如下表：

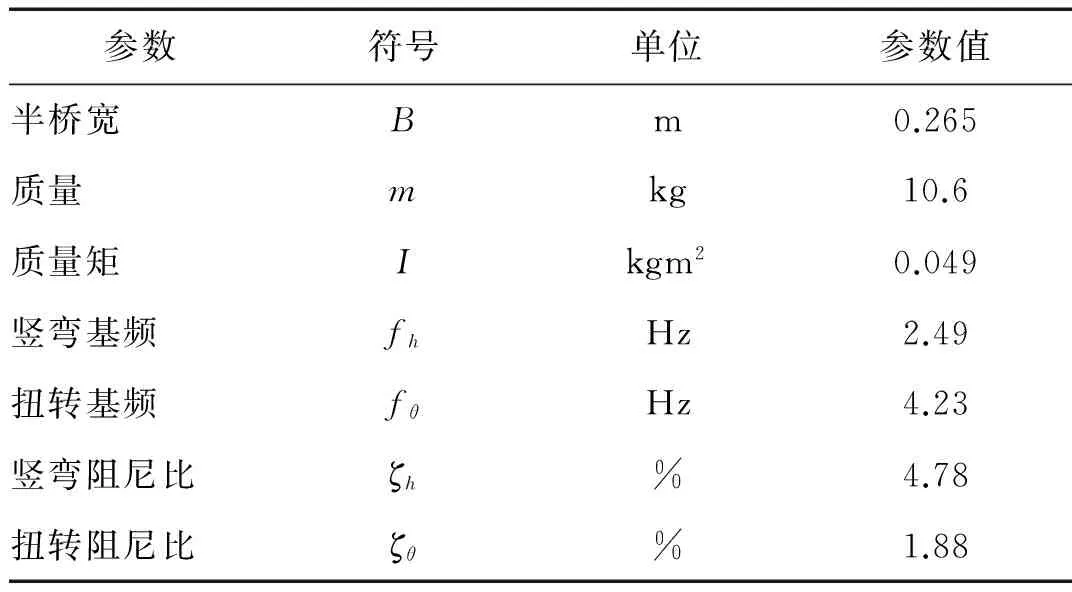
表1 系统参数Tab.1 System coefficients

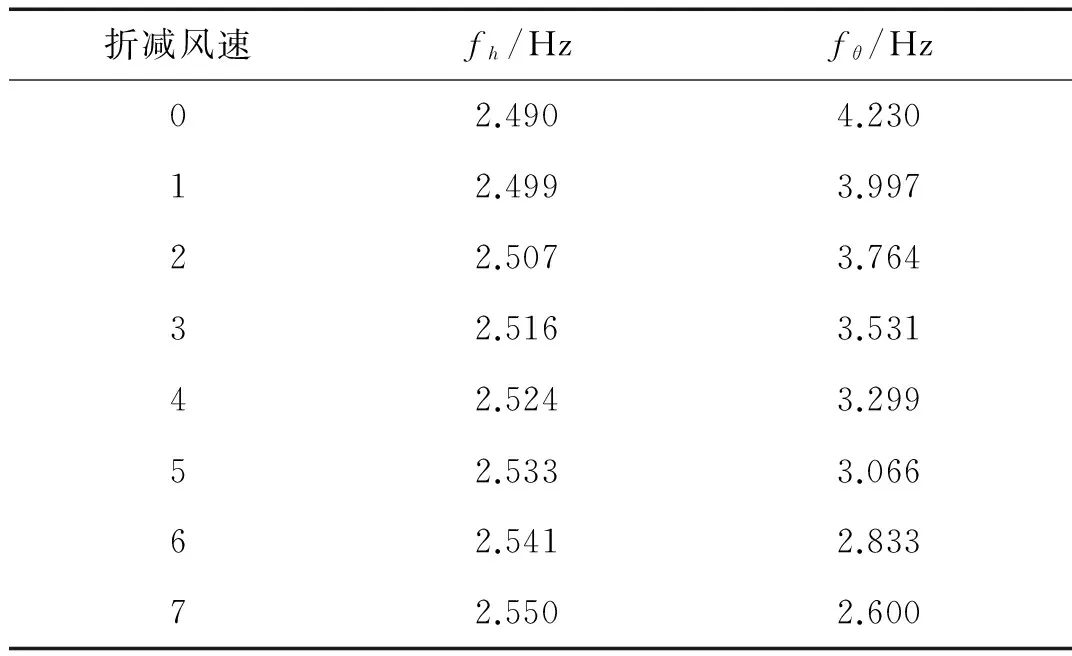
表2 频率预设值Tab.2 Frequency presets

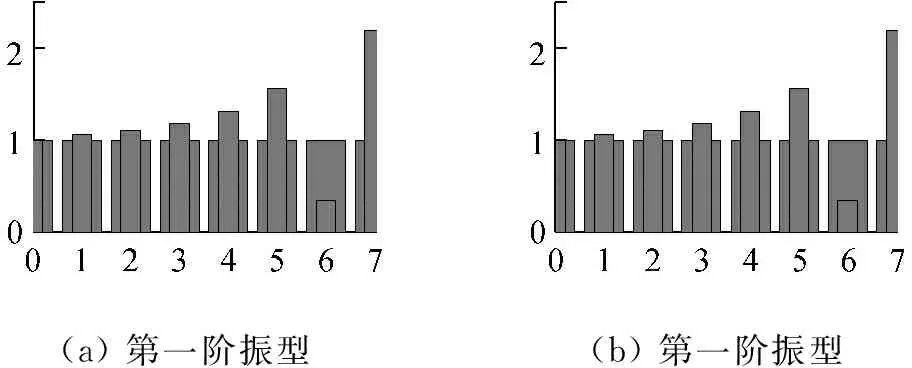
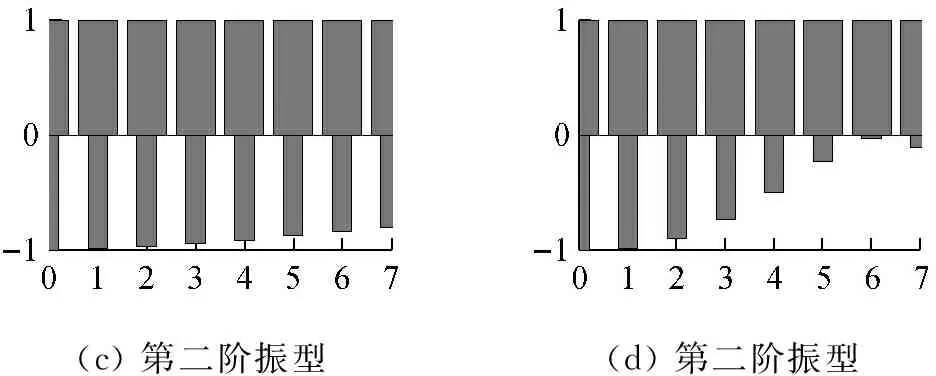
系统的固有频率能反应系统的某些特性，因此我们先做系统固有频率随折减风速变化的分析，结果如图3。从图中可以看出，系统的两阶固有频率随着折减风速的增大而逐步靠近，当这两阶频率最终趋于同一频率时，系统将失去稳定性，发生颤振现象。我们将此临界状态所对应的风速称作临界风速。由图4中看到，第一阶阻尼比在折减风速6的情况后，开始急速下降，也可分析得出系统趋于临界状态，当阻尼比由正变负时，系统发生颤振失稳。图5中的特征向量表现了随折减风速变化，系统振型的变化规律。

4.2 参数辨识

在上述推导中，对于主动控制模型所受激振力形式，没有做出特殊的假定。在主动控制模型的仿真实验中，我们采用了脉冲激励对系统施加外激励。仿真结果都是在采样频率128 Hz，采样时间400 s的采样条件下得到的。

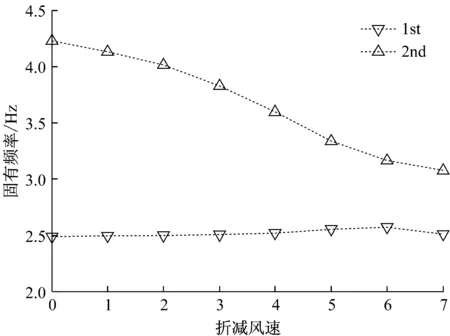
图3 固有频率的变化Fig.3 Eigen frequencies

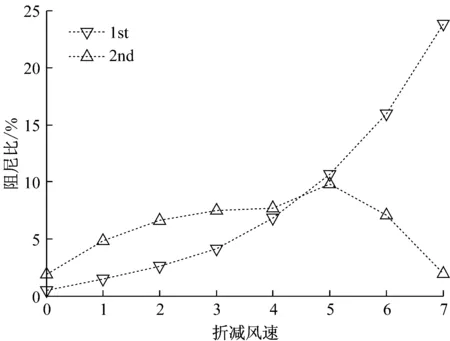
图4 阻尼比的变化Fig.4 Damping ratio

(a)第一阶振型(b)第一阶振型

(c)第二阶振型(d)第二阶振型

图5 振型的变化

Fig.5 Different modal

图6～图10是参数辨识结果，可以看出，利用本文的辨识方法所得到的控制参数与设定的参数几乎完全一致，这同时也验证了主动控制模型的合理性。从图6～图9可以看出，随着折减风速的增大，控制增益不断增大。图10表明反馈作用中心随折减风速增大而逐渐朝桥梁节段边缘移动。

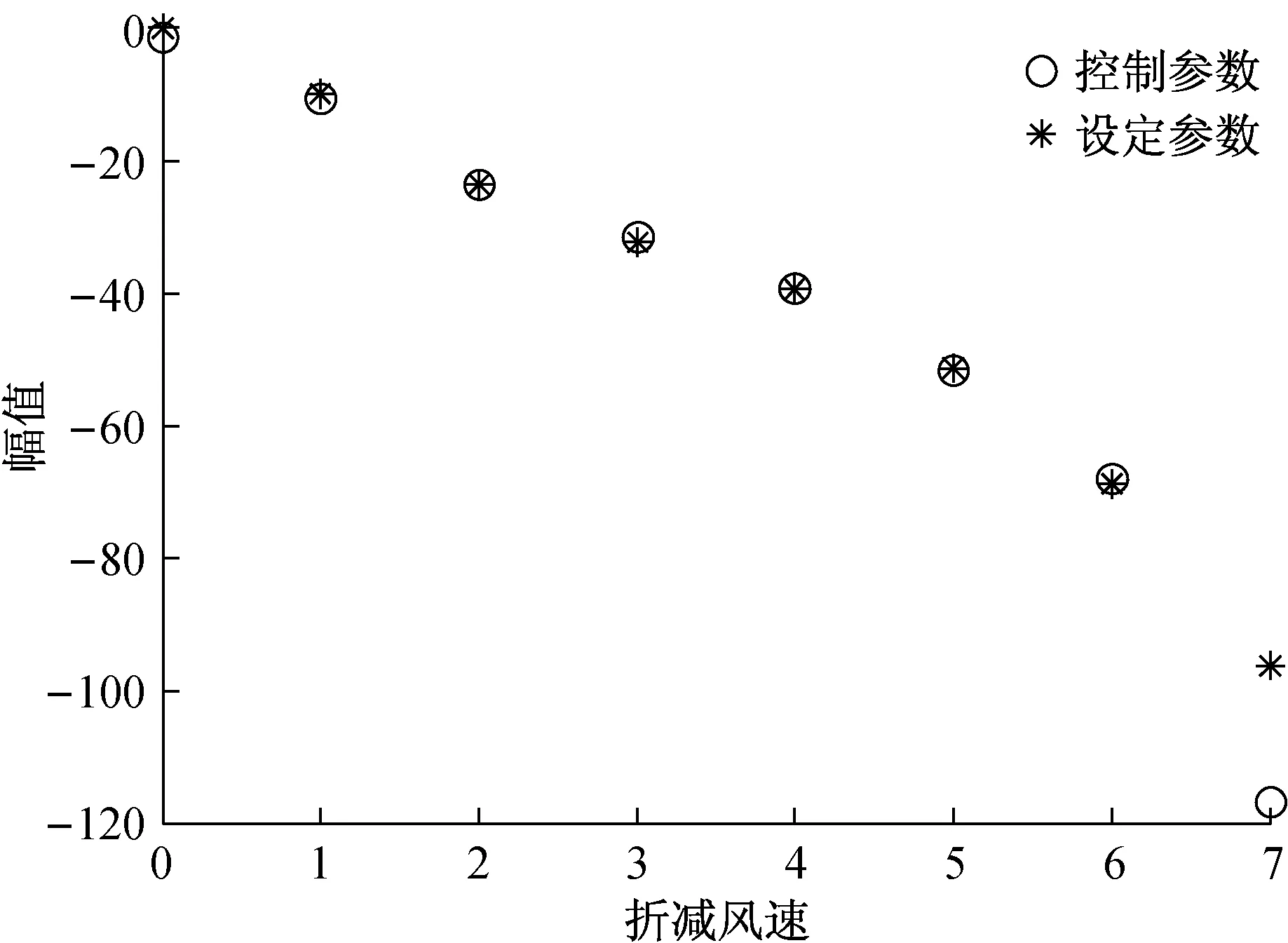
图6 Δh的变化Fig.6 Δh and wind speed

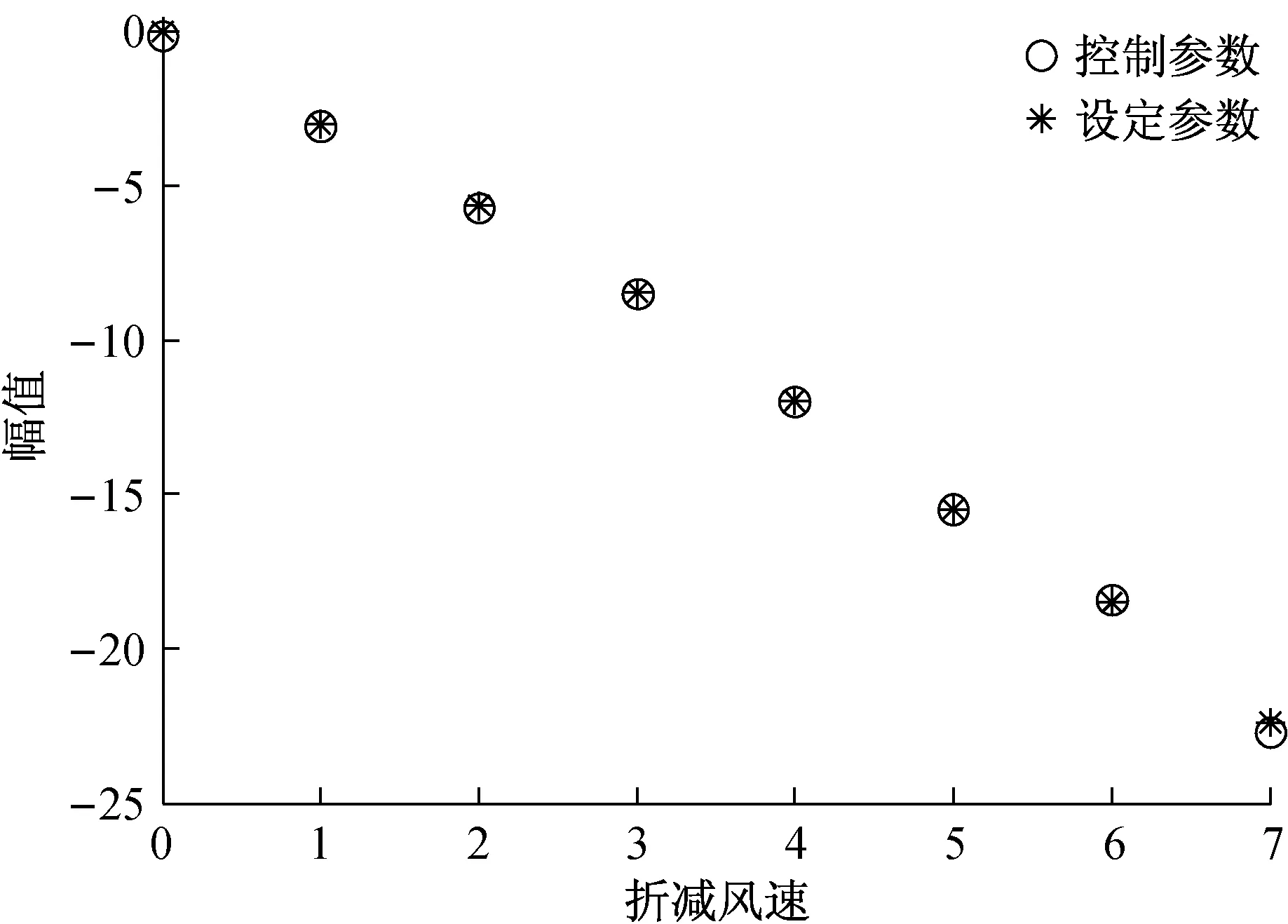
图的变化

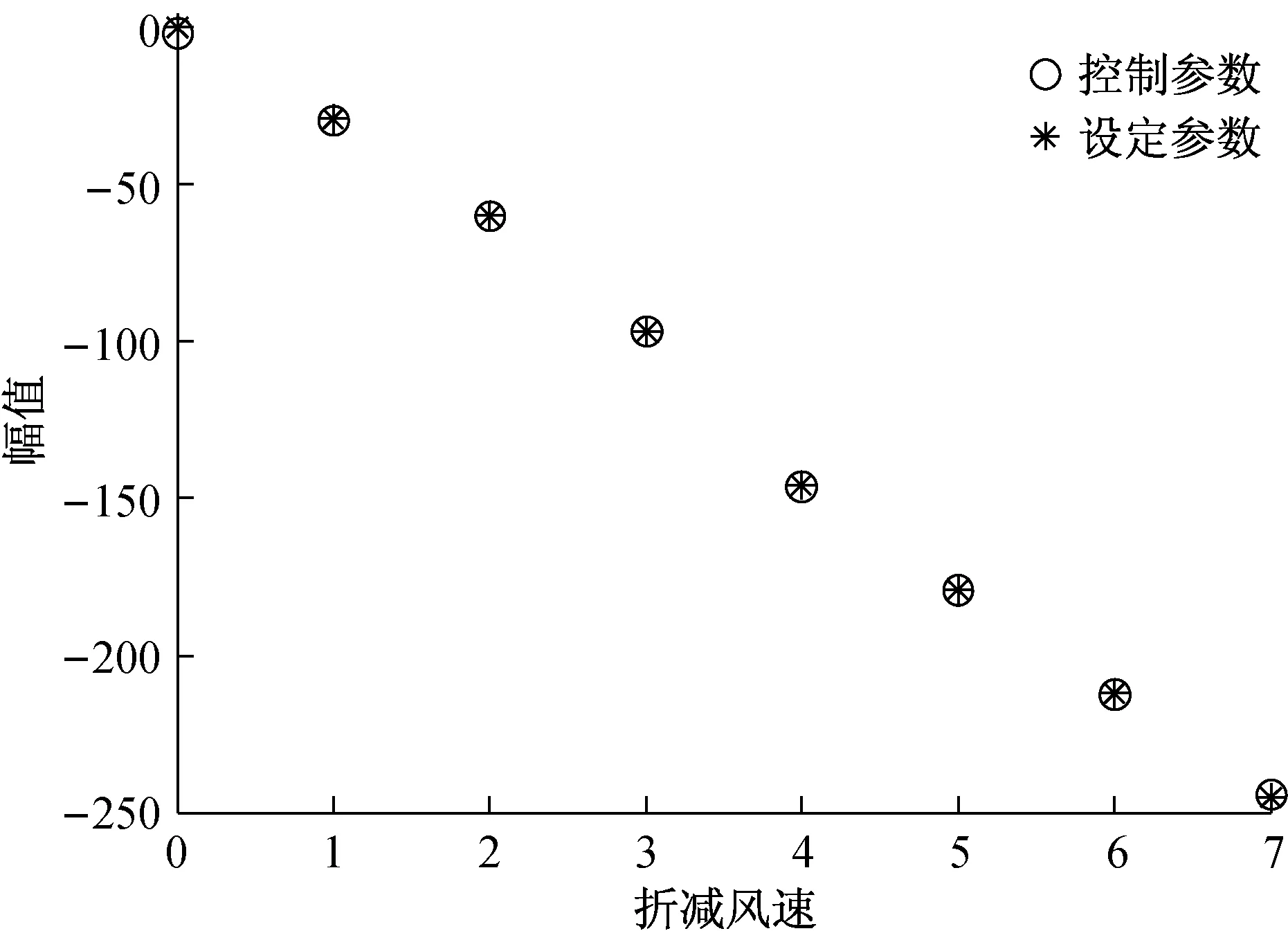
图8 Δθ振型的变化Fig.8 Δθ and wind speed

5 结 论

本文将干风洞的实验技术路线引入到桥梁节段模型的风洞实验模拟及参数辨识领域。在桥梁节段模型的刚体假设条件下，导出了通过PID反馈控制实现的与风洞条件下气动颤振行为保持一致的动力学模型，提出了具有5个独立控制参数的桥梁节段主动控制模型模拟含有8个颤振气动导数的节段风洞试验模型。

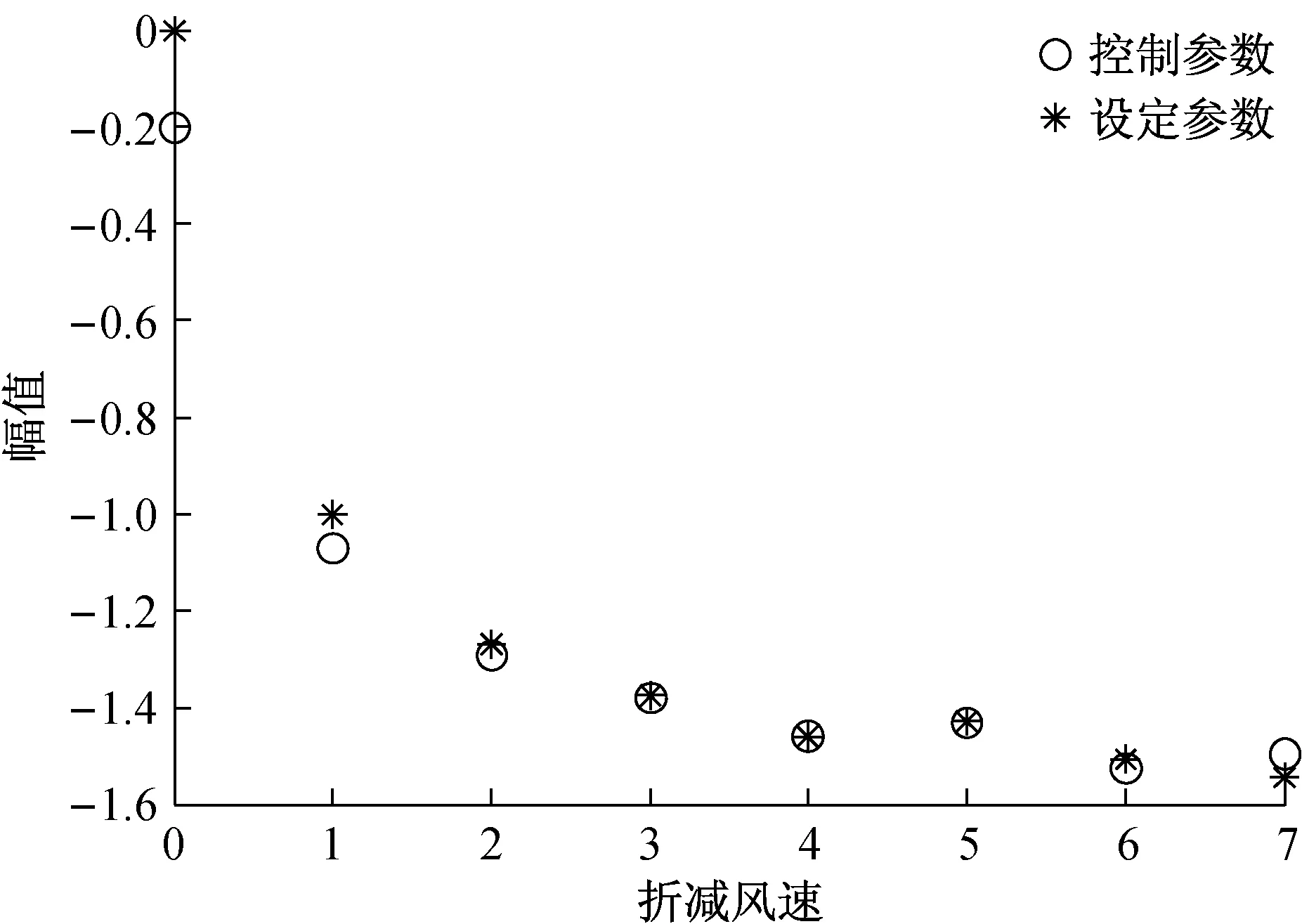
图的变化

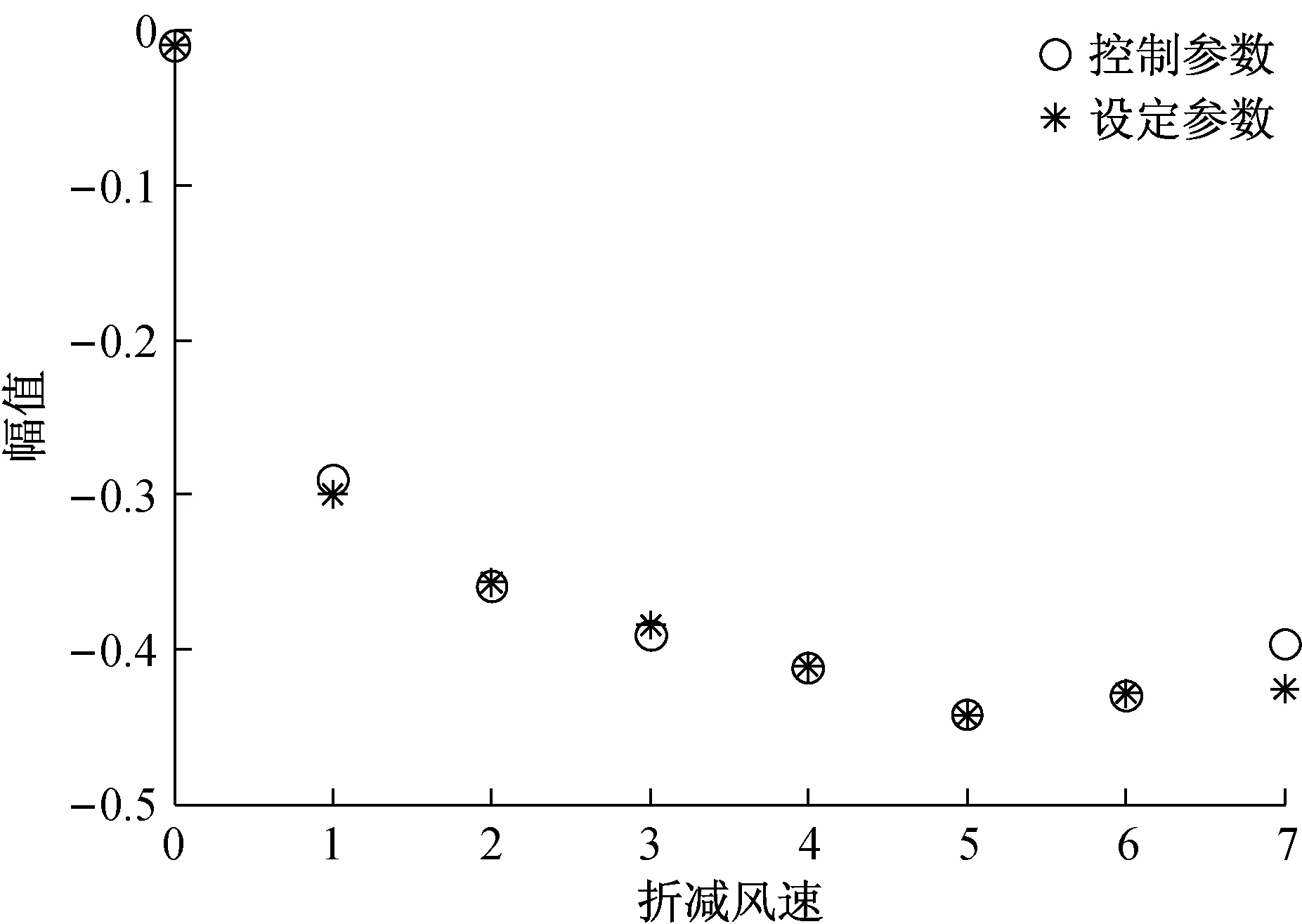
图10 反馈作用中心的变化Fig.10 β and wind speed

进一步设计了仿真实验技术路线，通过实验数据获取系统完备的频响函数矩阵，导出了基于复模态理论的左、右特征向量的辨识算法。基于文献[14]给出的风洞实验数据，重构了数值仿真模型，验证了本文提出的干风洞实验思路的可行性和合理性。

[1] SCANLAN R H, TOMO J J.Air foil and bridge deck flutter derivatives[J].Journal of Soil Mechanics & Foundations Div, 1971, 97(6): 1717-1733.

[2] SARKAR P P.New identification methods applied to the response of flexible bridges to wind[D].The Johns Hopkins University, Baltimore, Maryland, USA, 1992.

[3] GU M, ZHANG R, XIANG H.Identification of flutter derivatives of bridge decks[J].Journal of Wind Engineering and Industrial Aerodynamics, 2000, 84(2): 151-162.

[4] GU M, ZHANG R, XIANG H.Parametric study on flutter derivatives of bridge decks[J].Engineering Structures, 2001, 23(12): 1607-1613.

[5] BROWNJOHN J M W, JAKOBSENB J B.Strategies for aeroelastic parameter identification from bridge deck free vibration data[J].Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(13): 1113-1136.

[6] CHEN A R, HE X F, XIANG H F.Identification of 18 flutter derivatives of bridge decks[J].Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12): 2007-2022.

[7] CHOWDHURY A G, SARKAR P P.A new technique for identification of eighteen flutter derivatives using a three-degree-of-freedom section model[J].Engineering Structures, 2003, 25(14): 1763-1772.

[8] 许福友, 陈艾荣, 张哲, 等.确定桥梁模型颤振临界风速的实用方法[J].振动与冲击, 2008, 27(12): 97-100.

XU Fuyou CHEN Airong, ZHANG Zhe, et al.Practical technique for determining critical flutter wind speed of bridge model[J].Journal of Vibration and Shock, 2008, 27(12): 97-100.

[9] 黄方林, 陈政清.桥梁颤振气动导数识别的迭代法[J].振动与冲击, 2002, 21(2): 64-67.

HUANG Fanglin, CHEN Zhengqing.Iterative method for identification of flutter derivatives of a sectional bridge model[J].Journal of Vibration and Shock, 2002, 21(2): 64-67.

[10] 周锐，杨詠昕，葛耀君，等.平行双幅桥梁的颤振控制试验研究[J].振动与冲击, 2014,33(12): 126-132.

ZHOU Rui, YANG Yongxi, GE Yaojun, et al.Tests for flutter control of a twin-separate bridge[J].Journal of Vibration and Shock, 2014,33(12): 126-132.

[11] 丁泉顺，王景，朱乐东.桥梁断面颤振导数识别的耦合自由振动方法[J].振动与冲击, 2012, 31(24):5-8.

DING Quanshun, WANG Jing, ZHU Ledong.Coupled free vibration technique for identifying flutter derivatives of bridge decks[J].Journal of Vibration and Shock, 2012,31(24): 5-8.

[12] 许云涛, 吴志刚, 杨超.地面颤振模拟试验中的非定常气动力模拟[J].航空学报, 2012, 33(11): 1947-1957.

XU Yuntao, WU Zhigang, YANG Chao.Simulation of the unsteady aerodynamic forces for ground flutter simulation test[J].Acta Aeronautica of Astronautica Sinica, 2012, 33(11):1947-1957.

[13] ZHANG X X, CHEN L F, SONG H W.Self-contained eigenvector algorithm applied to the identification of aerodynamic derivatives of bridge model[J].Science China Technological Sciences, 2011, 54(5): 1134-1140.

[14] CAO B, SARKAR P P.Identification of rational functions using two-degree-of-freedom model by forced vibration method[J].Engineering Structures, 2012, 43: 21-30.

Simulation for a Bridge Section Model’s Wind Tunnel Test Based on Feedback Control

DENG Zhi, SONG Hanwen

(School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China)

When a bridge stays in a windy environment, the aerodynamic force makes it act as a non-classic system.For studying this, a five-parameter bridge segment model based on active control was proposed here to simalate a bridge section wind tunnel test model with eight flutter derivatives.According to the principle of equivalent force system, the proposed model constructed with the signal feedback technique coincided with the wind tunnel test model in the aspects of mathematics and mechanics.With a geometric transformation, the linear displacement signals measured in the wind tannel test could be transformed into the angular displacement signals.Meanwhile, the system’s FRF matrix was obtained with the MIMO analysis technique simply and accurately.Then the control parameters were identified with the left-right eigenvectors identification algorithm based on the complex modal theory.Through simulations, the rationality of the proposed model was validated.The results revealed the application prospect of the proposed model in bridge wind-induced vibration study.

wind-induced vibration; active control; modal analysis; parametric identification

国家自然科学基金(11272235)

2015-11-26 修改稿收到日期：2016-02-22

邓 智 男，硕士生，1989年生

宋汉文 男，教授，博士生导师，1962年生

O322

A

10.13465/j.cnki.jvs.2017.05.019