操作：让学生学得更好——基于数学操作的教学案例研究

靳　颖

一、操作——在活动中经历数学概念的形成

弗赖登塔尔曾说过：“学习这一活动最好的办法是做。”动手操作适合小学生的身心特点，手脑并用，于数学概念学习来说能收到事半功倍的效果。

例如，笔者在教学《圆锥体积》时，设计了如下的教学片断：

活动准备：给每个小组准备了若干个圆柱和圆锥：有等底等高的，有等底不等高，有等高不等底，也有既不等底也不等高的。

活动要求：在组长的带领下，借助这些圆锥和圆柱做实验，看看能否发现圆锥与圆柱体积之间的关系，并做好记录填在表格中。学生通过分组做实验后，汇报实验结果。汇报如下：

生1：我们组做了三次实验。

生2：我们组做了四次实验。

……

通过各小组的汇报，学生从中对比发现：等底等高的圆柱和圆锥体积之间存在一定的规律：圆锥的体积=圆柱的体积×。

上述的操作活动为学生提供了自主探究的机会和广阔的思维空间。他们自主选择学具，主动操作、讨论、对比、概括，发现了等底等高的圆柱和圆锥的体积之间存在的规律——圆锥的体积是圆柱体积的三分之一。

二、操作——在活动中渗透数学思想

数学思想方法蕴含在数学知识之中，尤其蕴含在数学知识的形成过程中，操作可以帮助学生经历这样的过程，体验蕴含其中的数学思想。

例如，笔者在教学《发现椭圆》时是这样设计的。

在学生正确判断三根小棒能否围成三角形的基础上，给出两根小棒想办法围三角形。如果把其中一根剪成两段（两段的长度均是整数），然后和另一根小棒共同围成一个三角形，一共有几种不同的围法？例如14厘米长的小棒可以进行拆分如下：

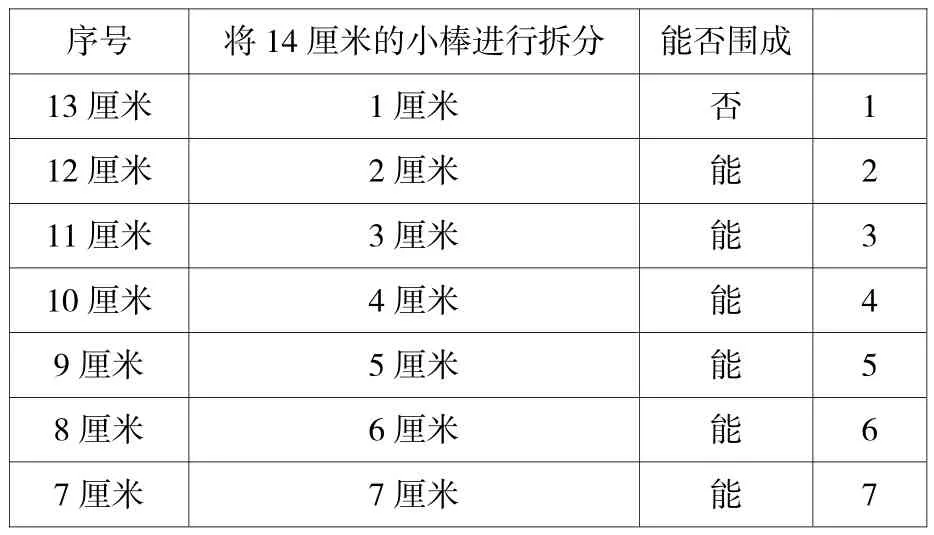
序号　将14厘米的小棒进行拆分　能否围成13厘米　1厘米　否　1 12厘米　2厘米　能　2 11厘米　3厘米　能　3 10厘米　4厘米　能　4 9厘米　5厘米　能　5 8厘米　6厘米　能　6 7厘米　7厘米　能　7

再用两根细绳代替两根小棒，分别长为12厘米和14厘米。将12厘米长的绳子拉直，两端固定在黑板上。再把14厘米长的两端也固定在那两个点上，然后找到第三个顶点，在纸板上画下这个顶点。如图：

接着问∶如果不要求截成整厘米数，又有多少种不同的围法呢？

学生操作学具并画出各点，得到下左图。

师∶大家想一想，如果我们将所有可能围成的三角形的第三个顶点都找到并画出来，它的轨迹会是怎样的？（学生想象可能是圆形也可能是椭圆。出示上右图）

再接着电脑动态演示如下：

经过这一连串的操作和演示，同学们可以确定这些点的轨迹是一个椭圆。

数学思想是潜隐于数学知识的发生发展过程中的内部之物，不易为学生直接把握。在上述活动中，先把14厘米的小棒截成两段长度是整厘米数的小棒，其方法是有限的，所围成的三角形的第三个顶点也是有限的。接着把14厘米的细绳分成两段长度是小数的小段，此时出现了无数种方法，相应围成的三角形的第三个顶点也是无限的。学生由此亲历了三角形第三个顶点个数由有限到无限的过程，感悟了极限思想。

三、操作——在活动中发展空间观念

对于小学生而言，操作及其经验是他们发展空间观念的基础。

笔者在教学《长方体和正方体的认识》时，设计了如下活动：

课前给每个小组准备了土豆和小刀，让学生通过切土豆，经历了如下的操作过程：

1.切之前先让学生观察土豆的形状，摸摸表面。在脑中想象切一刀之后土豆会有怎样的变化？先切一刀，摸一摸新切出的面，比较和切之前有什么变化。学生发现新出现的面是平平的。揭示面：简称“平面”（板书：面）。

2.想一想：如果再切一刀，土豆会发生什么变化？学生先想象，接着再切一刀，观察土豆此时又发生了什么变化？学生发现又新增了一个面，而且第二次切出的面与第一次切出的面相交于一条线，学生用手摸摸新增的线。揭示：两个面相交的线叫做棱（板书：棱）。

3.想一想：如果再切一刀呢？又会有什么变化呢？学生先在脑中想象。接着切第三刀，观察又发生了怎样的变化？发现切三刀之后，三条棱相交于一点，再次用手摸摸，感觉尖尖的。此时指出三条棱相交的点叫做顶点（板书：顶点）。

4.接着让学生想一想如果继续切下去，怎样才能把土豆切成一个长方体呢？

在操作之前，应该让学生先考虑如何操作，以及操作后土豆的形状。学生在操作之前就先想好了一定的步骤，但是这种想法还只是想象，需要实际操作来进行验证。对比土豆被切前后的变化，并用手摸一摸、看一看，直观感知长方体的面、棱、点，逐步建立表象，充分感知长方体的特征。在操作中学生经历了长方体特征形成的过程，学生的思维由形象上升到抽象，空间想象能力得到发展，为后续学习立体几何奠定基础。

四、操作——在活动中激发学习兴趣

教学中，我们要对教材进行适度的改编，化静为动，使学生在操作中产生学习的兴趣。

笔者在教学《厘米的认识》时，是这样设计的：

活动一：找出1厘米

学具袋里有四根小棒（长度分别是10厘米、5厘米、1厘米和0.5厘米），其中有一根长度是1厘米。你能把它找出来吗？

活动二：尺子验证

师：你们找到的这根小棒，长度到底是不是1厘米呢？（学生想到了可以用尺子量）通过量这根小棒，证明它的长度就是1厘米。且在量小棒的过程中认识了刻度尺，明确从0到1之间的线段长，就是1厘米。学生知道直尺上“0到1”之间这样长的一大格就是1厘米。进而明确：尺子上相邻的两个刻度数之间的长度就是1厘米。

活动三：找生活中的1厘米

学生纷纷找出身边的1厘米（有的学生还发现食指的宽度、纽扣的宽度正好也是1厘米……)

活动四：挑出1厘米

给出三条长度不同的线段（只有1条长度是1厘米），要求不用尺子，在三条中选出1厘米长的那条线段描出来。

活动五：估计1厘米

给出学生熟悉的物品（如橡皮、骰子、一元硬币等），要求先估一估谁的厚度大约是1厘米，并想办法验证它是不是1厘米。

在操作活动中，学生的眼、耳、口、手、脑多种感官处于一种积极活动的状态，通过找、量、描、估等操作活动，选取了学生熟悉的素材，架起了学习内容与生活实际之间的桥梁，使枯燥的概念变得鲜活起来，使乏味的课堂变得让人回味。学生通过找到“1厘米长的小棒”获得了成功的喜悦，用尺子量找到的1厘米长的小棒，验证了自己找的是正确的，获得了自信。亲历“1厘米”的形成过程，让学生真正感受到学习数学的必要性，产生我爱学的强烈欲望。