基于加速度测试及模糊模型的弹丸侵彻混凝土深度实时预测方法

张冬梅，高世桥，刘海鹏，牛少华

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

基于加速度测试及模糊模型的弹丸侵彻混凝土深度实时预测方法

张冬梅，高世桥，刘海鹏，牛少华

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

为了对卵形弹垂直侵彻半无限厚混凝土目标的侵深进行实时预测，提出了一种基于实测加速度值及模糊模型的计算方法。该方法根据瞬时速度的不同将侵彻过程分成了高速侵彻、中速侵彻和低速侵彻三个阶段，并分别采用不同的模型对每个阶段的减加速度、速度和侵彻深度进行了描述。通过判断减加速度的计算误差，自动确定了高速侵彻阶段与中速侵彻阶段以及中速侵彻阶段与低速侵彻阶段的截点速度。同时，利用实测的全弹道加速度曲线，实时计算了侵彻过程的初始冲击速度。将实验后所测得的侵彻深度与模型预测的侵彻深度进行比较，结果表明该预测方法可以对侵彻深度进行准确地实时计算。

侵彻;混凝土;模糊模型;实时侵彻深度

随着现代武器技术的发展，在战争中保护和隐藏重要战略目标的方法发生了很大的变化。硬目标侵彻武器已经成为摧毁高价值战略目标的重要手段，完成侵彻武器自适应起爆控制的硬目标灵巧引信的作用也变得越来越重要。硬目标侵彻引信通过感应和处理侵彻深度、侵彻过载和侵彻层数等信息来决定起爆时刻。因此，在侵彻过程中正确地预测和识别出实时侵彻深度对于硬目标灵巧弹丸实现最大毁伤是至关重要的。

为了得到侵彻深度，人们基于大量试验总结了众多的经验公式和模型算法，归纳起来主要分为两类：一类模型是直接描述侵彻深度，如PETRY公式[1]，ACE公式[3-4]，NDRC公式[5]，BRL公式[6-8]等；另一类则首先对侵彻阻力或侵彻过程中的减加速度进行描述，然后推倒出侵彻深度，如FORRESTAL等[9-13]基于空穴膨胀理论和靶场试验不断完善了的侵彻阻力模型;GAO等[14]考虑到混凝土材料的可压缩性提出的法向膨胀理论;HOLMQUIST等[15]提出的混凝土的动态强度模型等。然而这些模型都是基于一定的初始冲击速度提出的，要么只适用于低速或低中速冲击，要么只适用于高速冲击。

实际上，针对半无限厚靶体，无论初始冲击速度多大，侵彻过程都是一个速度衰减的过程。因此，所谓低速或高速，不仅是针对不同次的射击侵彻，也针对同一次射击侵彻的不同阶段。那么，什么速度属于低速，什么速度属于中速，而什么速度又属于高速，却是个模糊的概念。为了有效统一各种模型，GAO等[16]提出了一种适应不同冲击速度的侵彻模型，即混凝土目标侵彻阻力的模糊模型，这个模型在描述整个侵彻过程时取得了良好的效果，但该方法无法实现侵彻深度的实时计算。

目前，实际工程中常用的方法是对侵彻过程中弹体的刚体加速度进行积分来获得侵彻深度。为了提取刚体加速度，需要对实测数据进行滤波。由于侵彻时间非常短，信号处理很难满足实时性要求。因此，提出一种基于实测加速度和模糊模型的可以实时计算侵彻深度的计算方法。

该方法将卵形弹垂直侵彻半无限厚混凝土目标的过程分成高速侵彻、中速侵彻和低速侵彻三个阶段，根据惯性效应和强度效应所起作用的不同，分别提出不同的模型对每个阶段进行描述。在计算过程中，通过判断减加速度的计算误差，可以自动确定高速侵彻阶段与中速侵彻阶段以及中速侵彻阶段与低速侵彻阶段的截点速度。利用全弹道加速度曲线，对侵彻过程的初始冲击速度进行实时计算。为了更好地验证计算结果的正确性与可靠性，本文还将计算结果与实验测得的数据进行了对比。

1 模糊计算模型

综合前人针对不同速度的各种侵彻模型，如图1所示的质量为m的卵形弹丸以速度v0垂直侵彻混凝土的过程中，靶体作用在弹体上的阻力通常由两部分构成：一部分是由于速度引起的阻力，即惯性阻力，它主要取决于弹体的实时侵彻速度；另一部分是由于靶体材料强度引起的阻力，即强度阻力，它主要取决于目标的强度，该强度是与材料应变率相关的动强度。许多工程试验表明，在侵彻速度较小时，强度阻力起主导作用；而当侵彻速度比较大时，惯性阻力起主导作用。当侵彻速度介于两者之间时，强度效应和惯性效应会同时影响阻力。

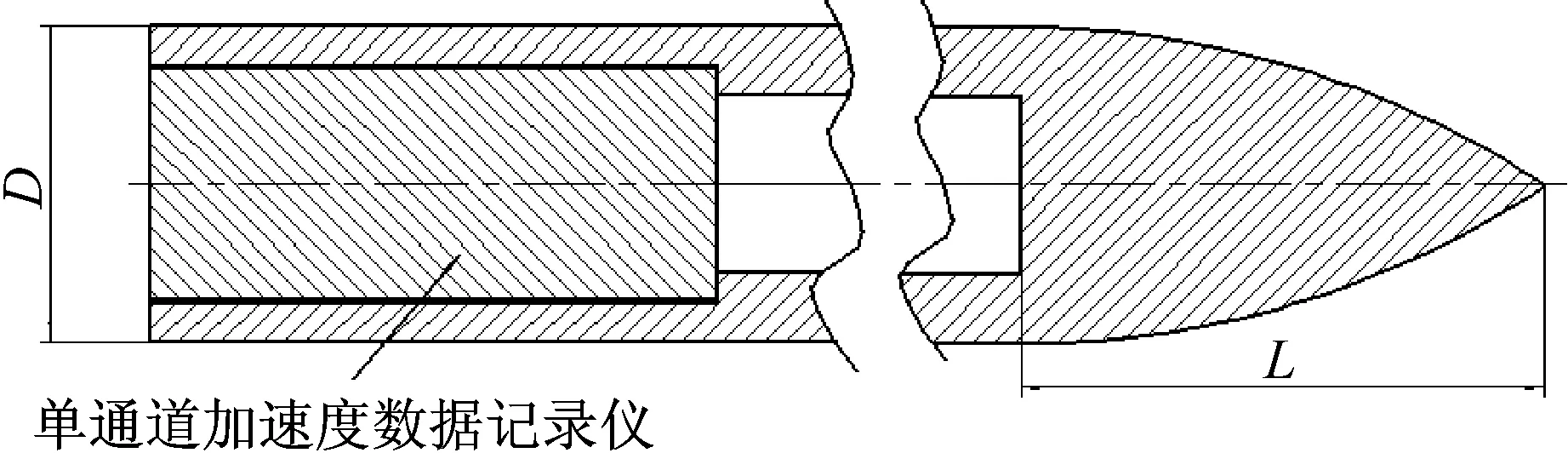
图1 卵形弹几何尺寸图Fig.1 Geometry for the ogive-nose rod

因此，作用在弹体上的减加速度也可以分为两部分：由惯性效应产生的减加速度ad，由强度效应产生的减加速度as。可将其表示成如下的通用形式：

a=as⊕ad

(1)

式中:符号⊕不是简单的算术和，而是代表一种逻辑求和。因为as和ad来源于不同的模型，不能将其简单地累加起来。参考高世桥等人提出的模糊模型中关于混凝土材料模糊动态特性的概念，应用模糊数学中的方法，定义一个变量α作为隶属度，它包含两项，即as和ad。这两个变量分别代表侵彻过程中强度效应和惯性效应的影响程度。引入隶属度后，式(1)就可以写为

a=αsas+αdad

(2)

式(2)中as和ad分别是弹体侵彻混凝土过程中作用在弹体上的减加速度隶属于强度效应的程度和隶属于惯性效应的程度。它们满足下面的关系式：

αs+αd=1

(3)

按照上述的分析，隶属度α={αd,αs}主要取决于侵彻速度。高速侵彻时，可以将作用于弹体的减加速度看作由惯性效应导致的，此时隶属度可描述为

μ={1.0,0.0}

(4a)

低速侵彻时，可以将作用于弹体的减加速度看作由强度效应导致的，其中强度效应起很重要的作用，此时的隶属度可表示为

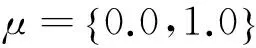
(4b)

中速侵彻时，作用于弹体的减加速度既不能被简单地看作是强度效应所致也不能被简单地看作是惯性效应的结果。因此，有必要将其视为一种模糊效应。此时的隶属度可表示为

α={αd,αs}

(5)

其中的元素满足式(3)中的归一化关系。

隶属度α可描述不同冲击速度情况下作用在弹体上的减加速度。式(4a)和(4b)分别给出了高速和低速冲击时的极端情况，而对于中速冲击的情形，通常需用式(5)的一般形式来描述。

依据该模糊模型并考虑侵彻过程的连续性，侵彻过程中弹体的速度和侵彻深度也可以类似地表示为强度作用和惯性项作用之和，即

v=αsvs+αdvd

(6)

z=αszs+αdzd

(7)

式中:vs和vd分别为低速侵彻速度和高速侵彻速度；zs和zd分别为低速侵彻深度和高速侵彻深度。隶属度可以表示成实时侵彻速度的线性函数，即

(8)

(9)

便于描述，本文将不同侵彻阶段的分界速度称作截点速度。则v1为高速侵彻阶段和中速侵彻阶段的截点速度，v2为中速侵彻和低速侵彻的截点速度。截点速度不是固定值，对于不同的侵彻过程它的值是不同的。

2 作用在弹体的减加速度分析

侵彻过程中减加速度包含两大项，一项是由惯性效应导致的惯性项，另一项是由强度效应引起的强度项。对于不同的侵彻速度，强度效应和惯性效应的作用程度也不同。随着侵彻速度的提高，惯性作用越来越显著，强度作用越来越微弱；而随着侵彻速度的降低，强度作用却越来越明显，相对惯性作用来说变得越来越重要。下面分别对由惯性效应和强度效应所产生减加速度进行分析。

2.1 惯性效应

当只考虑惯性效应时，侵彻可以分成以下两段：

2.1.1z≤2D

当弹丸刚与目标接触时，弹丸头部与目标表面相交面积较小，侵彻减加速度较小。随着弹丸侵彻的不断深入，弹丸头部与靶板的相交面不断增大，侵彻减加速度也不断增加，当弹丸头部完全侵入目标时，侵彻减加速度接近最大值，此时的侵彻深度约等于弹丸直径的两倍。根据前人的研究结果，该阶段的减加速度除与速度有关外，与侵彻深度成线性关系[17-18]。根据以上的侵彻规律，当侵彻深度z小于2D时，作用于弹体的减加速度可以表示为

且z≤2D

(10)

式中:A*代表包括口径、长径比、弹靶材质等弹靶参数对阻力大小的影响;a为作用在弹体上的减加速度;v为侵彻过程中的速度;z为侵彻深度。

参数A*利用实测减加速度值采用线性回归的方法进行计算。已知试验中采样周期为T，采样点序号为i且i=0,1,2,…,N，其中N为采样点数。对应的时刻可表示为ti=(i-1)T，根据方程(10)，当z≤2D时，离散采样点的减加速度可表示为

且z≤2D

(11)

若将减加速度的实测值用yi表示，与计算值ai的差为εi=yi-ai，即

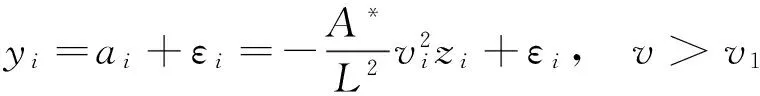
(12)

v>v1且z≤2D

(13)

v>v1且z≤2D

(14)

因此参数A*的估计值为

且z≤2D

(15)

实际中的A*是经过几次迭代来确定的。在确定迭代初值时，vi和zi的值采用对yi进行积分的方法进行给出，根据计算误差再对其进行迭代调整。则有

(16)

考虑到计算的实时性，计算A*的采样点数N可根据实际情况初步确定一个值，随着采样点数的增加再进行修正。

式(16)中，v0为初始冲击速度。对于大型导弹，初始冲击速度可由制导系统自动获取；而对于小型侵彻弹丸的初始冲击速度可利用测得的减加速度进行计算。针对本文的实际侵彻条件，该值可通过如图2所示的全弹道加速度值进行计算。由图可知在侵彻产生的减加速度值的前面有一段很显著的震荡，这是由于弹体冲破炮口的密封薄膜导致的。炮口到靶面的距离是已知的，分别读取弹体破膜的时刻和撞靶的时刻可以获得弹体通过该距离所经历的时间，如果将弹丸的该段飞行视为匀速直线运动，则可以计算出侵彻过程的初始冲击速度v0。

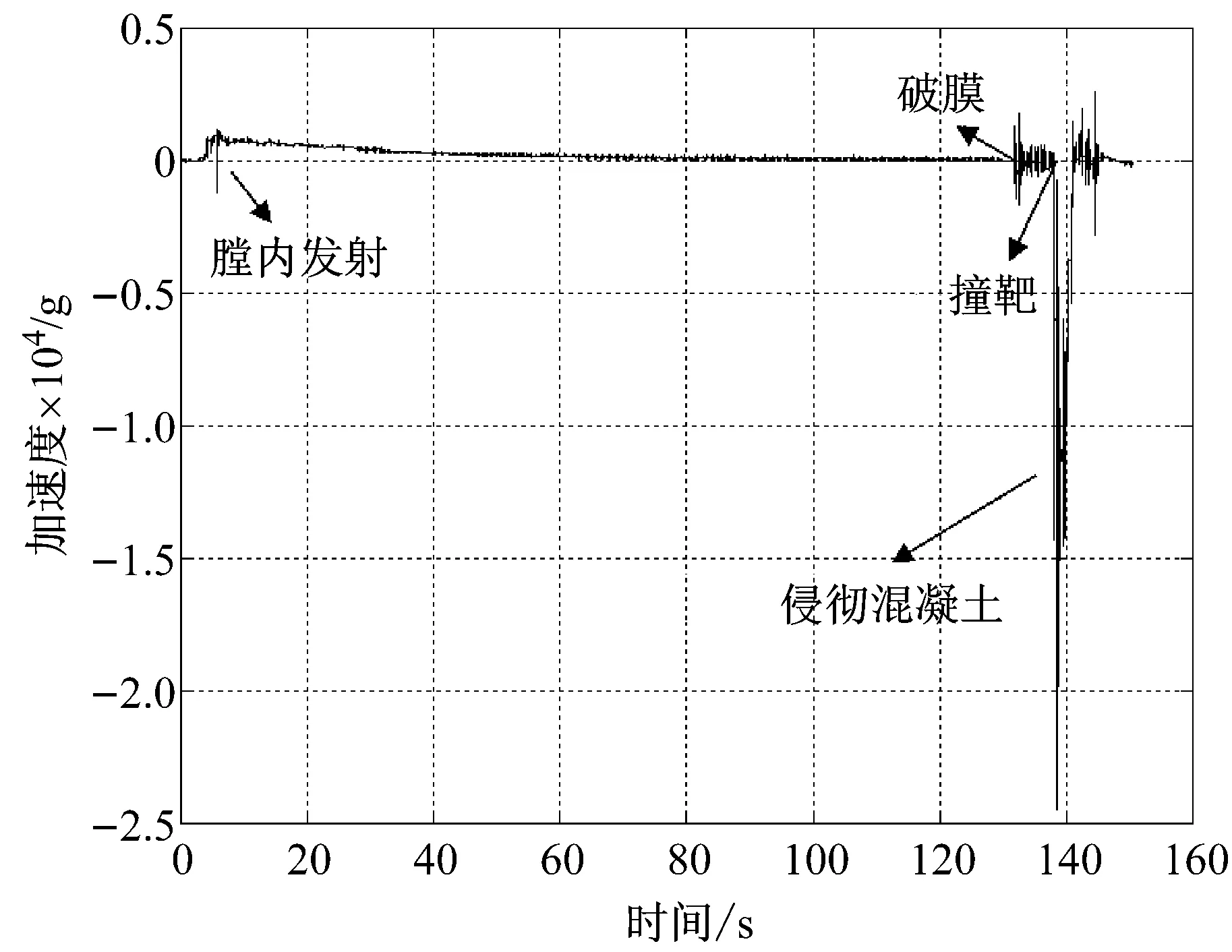
图2 全弹道加速度曲线Fig.2 Acceleration in whole trajectory

2.1.2z>2D

当侵彻深度z>2D时，作用于弹体的减加速度可以表示为

且z>2D

(17)

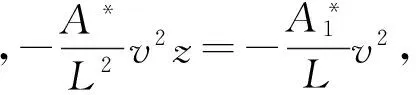
(18)

2.2 强度效应

当只考虑惯性作用时，由于影响强度项的主要因素是靶体的参数，并且这些参数都是常数，因此，作用在弹体上的减加速度可表示成

(19)

式(19)中B*为与弹体和靶体参数有关的常数。B*可采用多次观察求平均值的方法求得系数B*的估计值。由方程(19)可知加速度可表示为

(20)

因此，系数B*的估计值为

(21)

3 实时计算侵彻深度模型

针对半无限目标，由于弹丸在初始冲击阶段为高速侵彻，在侵彻过程中不断减速最终停止，因此，可以将整个侵彻过程分成三个阶段：高速侵彻阶段，中速侵彻阶段和低速侵彻阶段。根据模糊算法可知，不同侵彻阶段的隶属度取值是不同的。

3.1 高速侵彻

当αs=0,αd=1时，侵彻惯性项占主导地位，影响惯性项的主要因素是弹体的速度，我们将这一阶段的侵彻过程称为高速侵彻(v>v1)。高速侵彻又可以分成两个阶段。

3.1.1z≤2D

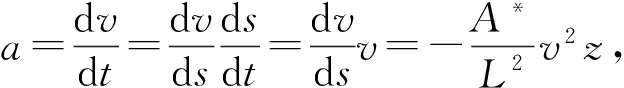
(22)

根据初始条件v=v0(t=0),z=0(t=0)对式(22)积分可得

且z≤2D

(23a)

求解该常微分方程便可计算出实时侵彻深度。相应的实时侵彻速度和加速度分别可表示为

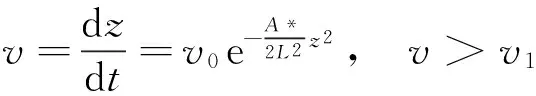
(23b)

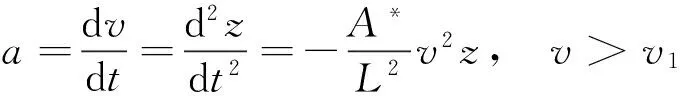
(23c)

3.1.2z>2D

当侵彻深度z>2D时，作用于弹体的减加速度可以表示为

且z>2D

(24)

两边取对数并根据初始条件t=0时v=v01，z=0，其中v01是z≤2D段的最终速度，可得

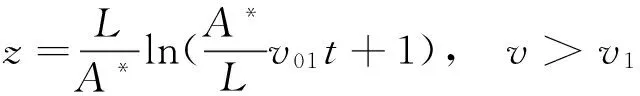
(25a)

(25b)

(25c)

3.2 低速侵彻

当αs=1，αd=0时，侵彻阻力中的强度项占主导地位，该过程称为低速侵彻(v≤v2)。在大应变、大应变率和高压力的环境下，混凝土材料的强度相对于静态条件是有所改变的，该强度与材料的应变率密切相关。该阶段作用在弹体上的减加速度可表示成

(26)

式(26)中B*为与靶体材质和强度有关的常数。根据牛顿第二定律可得

(27)

对其进行积分，根据初始条件t=0时v=v2，z=0，可获得位移、速度和加速度分别为

(28a)

(28b)

(28c)

3.3 中速侵彻

当0<αs<1,0<αd<1时，侵彻加速度可以表示为强度项和惯性项之和，该阶段称为中速侵彻。

将方程(25b)和方程(28b)代入方程(6)可得

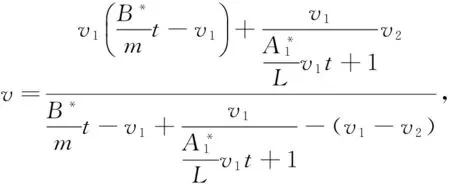
v1≥v>v2

(29a)

(29b)

v1≥v>v2

(29c)

3.4 截点速度

截点速度是确定速度段的关键参数，也是有效使用模糊模型的关键所在。在文献[16]中，依据工程实际情况，人为的确定了相应值，本文认为这样不一定符合实际情况。因此提出了依据误差来确定截点速度的方法。

当侵彻模型不能正确描述侵彻过程时，减加速度的计算值相对于测量值将会出现较大的误差。考虑到实测减加速度的特点，本文规定：当连续20个离散采样点的相对误差大于0.5%时，认为本模型不再适用，需要改变模型进行计算。因此，采用高速侵彻模型进行计算时，连续20个离散采样点的相对误差大于0.5%的起始时刻的瞬时侵彻速度即是高速侵彻段和中速侵彻段的截点速度v1。类似地，采用中速侵彻模型进行计算时，连续20个离散采样点的相对误差大于0.5%的起始时刻的瞬时侵彻速度即是中速侵彻段和低速侵彻段的截点速度v2。

4 侵彻实验

侵彻实验采用的弹丸几何尺寸,如图1所示，靶板为混凝土。弹体和靶体的相关参数,如表1所示。弹丸的头径比为3，材料为钢。

表1 弹体和混凝土靶参数Tab.1 Parameters of projectiles and targets

侵彻实验的加载平台为152 mm空气炮，弹丸中的单通道加速度测试系统可以获得如图2所示的全弹道的加速度曲线。通过放置在混凝土靶前的高速摄像系统，可以观测侵彻过程，并通过对动画过程的分析获得初始冲击速度。如图3所示为一组侵彻过程的截图，最终侵彻深度可以测得。

(a)

(b)

(c)

(d)

5 计算与实验对比

通过本文提出的算法可以计算出弹丸的初始冲击速度、加速度、速度和侵彻深度。为了验证算法的正确性，通过初始冲击速度分别为538 m/s、700 m/s和800 m/s的侵彻实验获得了相应的加速度和侵彻深度。由第2部分的方程计算得到的加速度时程曲线、速度时程曲线和侵彻深度时程曲线分别如图4～6所示。图中的三条曲线撞击速度分别为538 m/s、700 m/s和800 m/s。

图4 侵彻过程中减加速度时程曲线Fig.4 Deceleration versus time predictions

图5 侵彻过程中速度时程曲线Fig.5 Velocity versus time predictions

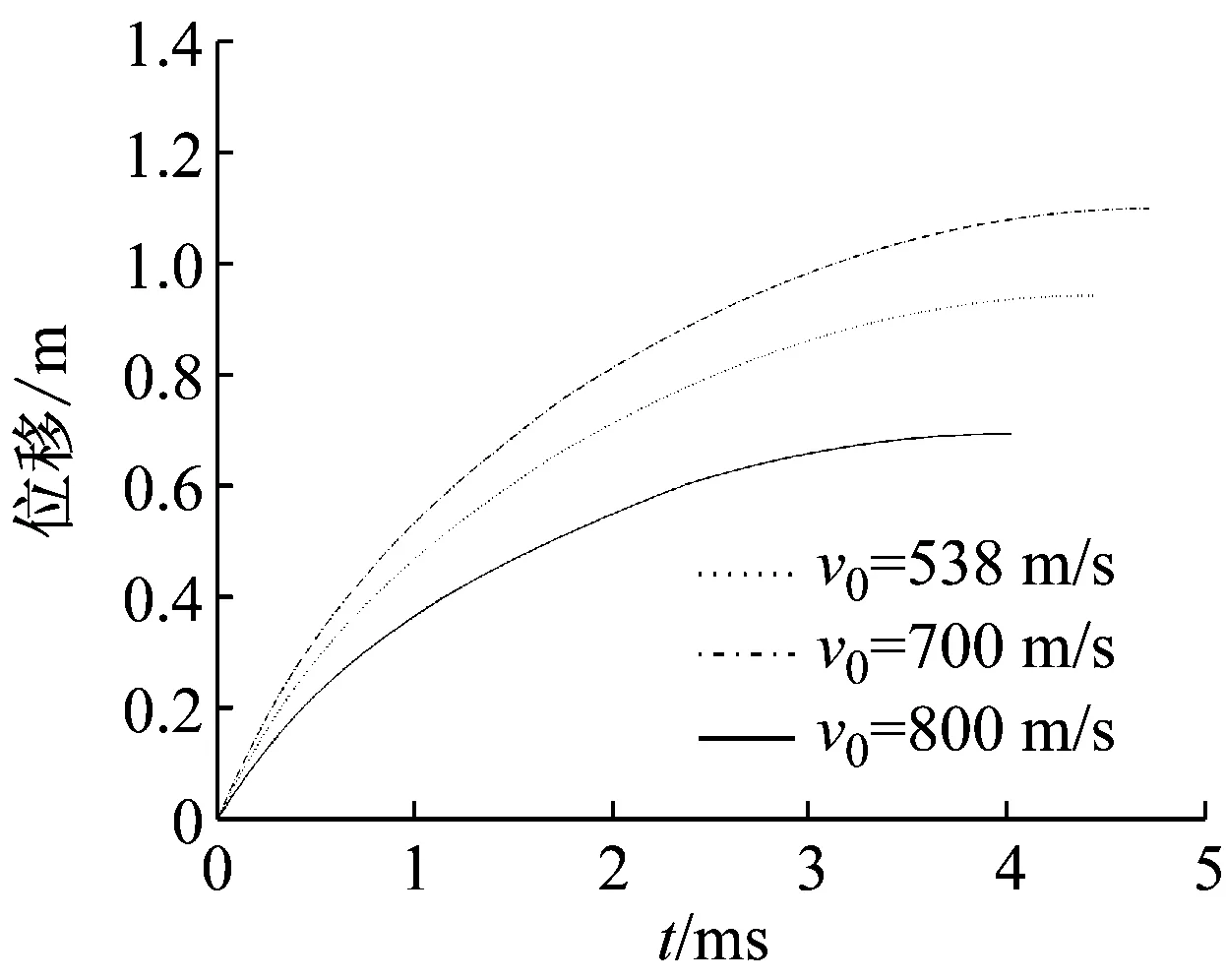
图6 侵彻深度时程曲线Fig.6 Displacement versus time predictions

由图4～6可知，加速度峰值、侵彻时间和最终侵彻深度都随着初始冲击速度的增加而增大。由图4可知当初始冲击速度为800 m/s时过载峰值大约为8万g，当初始冲击速度为700 m/s时过载峰值大约为7万g，当初始冲击速度为538 m/s时过载峰值大约为5.6万g。从图5可以看出，侵彻时间大约为4 ms。

通过对实测减加速度进行积分可以得到侵彻速度和侵彻行程。图7～9分别为初始冲击速度为800 m/s、700 m/s和538 m/s时分别通过本文所提出的方法计算和实验测得加速度时程曲线。相应的侵彻深度如表2所示，表中还分别给出了初始冲击速度的测量值和计算值。

图7 初始冲击速度为800 m/s时的减加速度曲线
Fig.7 Deceleration versus time with impact velocity 800 m/s

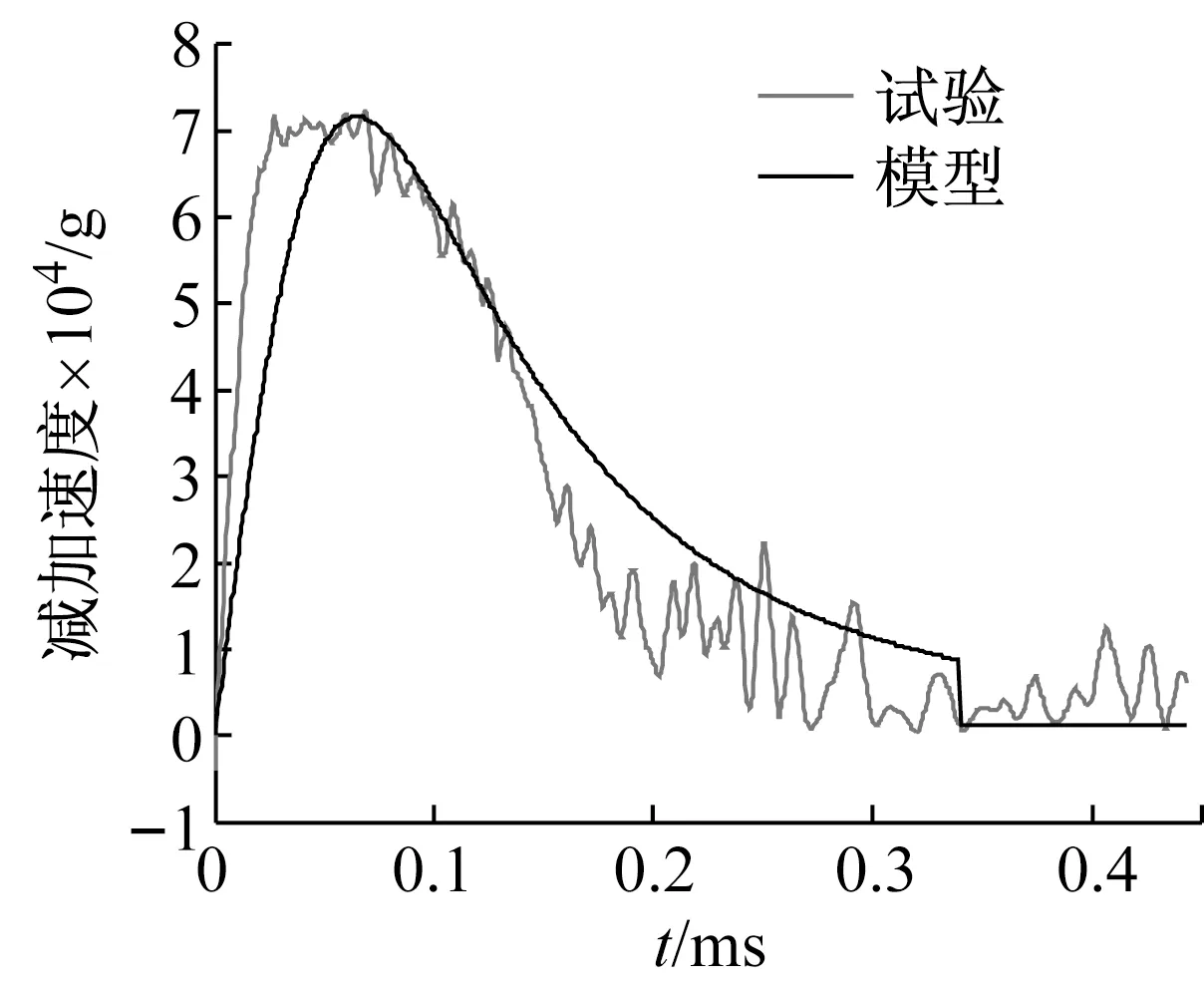
图8 初始冲击速度为700 m/s时的减加速度曲线
Fig.8 Deceleration versus time with impact velocity 700 m/s

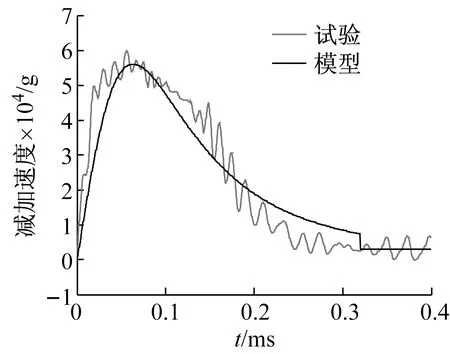
图9 初始冲击速度为538 m/s时的减加速度曲线
Fig.9 Deceleration versus time with impact velocity 538 m/s

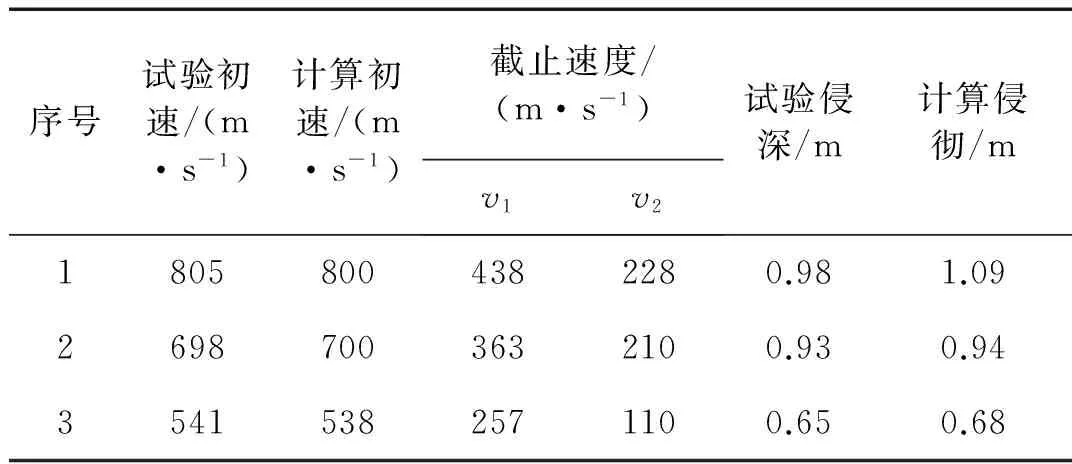
表2 计算及实验结果Tab.2 Data summary from the experiments and models

从图7～9可得对于不同初始冲击速度的侵彻过程模型计算值与实验测量值比较吻合。从表2可以看出本文提出方法的计算值与实测侵彻深度都很接近。因此，本文所提出的方法可以正确地实时地计算侵彻深度。

6 结 论

通过卵形头部弹丸垂直侵彻半无限混凝土靶的试验，获得了几组完整有效的加速度数据，同时测得了相应的初始冲击速度和侵彻深度。利用实测的全弹道加速度数据，获得了初始冲击速度。基于弹丸侵彻混凝土过程的减加速度数据，提出了一种能够实时计算侵彻深度的模糊算法。该方法将侵彻过程分成了高速侵彻阶段、中速侵彻阶段和低速侵彻阶段。高速侵彻阶段忽略了强度效应的作用，认为惯性效应起主导作用；低速侵彻阶段则忽略了惯性效应，只考虑了强度项；中速侵彻过程则同时考虑了强度效应和惯性效应的作用，并通过模糊模型中的隶属度对两种效应的作用进行了叠加。针对不同的侵彻过程，通过判断减加速度的计算误差，自动确定了高速侵彻阶段与中速侵彻阶段以及中速侵彻阶段与低速侵彻阶段的截点速度。

使用本文提出的方法不但对侵彻深度实时地进行了计算，而且还计算出了相应的速度和减加速度。将实测的侵彻深度、减加速度以及初始冲击速度与计算结果进行比较，可以看出本文提出方法的计算值与实测数据都很接近，因此该方法可以正确地描述整个侵彻过程并且可以对侵彻深度进行实时计算。

该方法将口径、长径比、弹靶材质等弹靶参数都通过两个待定参数A*和B*反应在模型中，截点速度可以自动确定，因此易于在实际工程中应用，同时实时地计算侵彻深度对于实时起爆控制系统也是很有价值的。

[1] BETH R A.Penetration of projectiles in concrete[R].PPAB Interim Report 1941.

[2] CHELAPATI C V, KENNEDY R P, WALL I B.Probabilistic assessment of aircraft hazard for nuclear power plants[J].Nucl.Eng.Des., 1972, 19:333-364.

[3] GWALTNEY R C.Missile generation and protection in light water-cooled reactor power plants[R].ORNL NSIC-22.Oak Ridge, TN: Oak Ridge National Laboratory 1968.

[4] LI Q M, REID S R, WEN H M, et al.Local impact effects of hard missiles on concrete targets[J].Int.J.Impact Eng., 2005, 32(1):224-284.

[5] ACE.Fundamentals of protective structures[R].Report AT1207821, Army Corps of Engineers, Office of the Chief of Engineers 1946.

[6] NDRC.Effects of impact and explosion[R].Summary Technical Report of Division 2, vol.1, National Defence Research Committee, Washington, DC, 1946.

[7] KENNEDY R P.Effects of an aircraft crash into a concrete reactor containment building[M].Anaheim, CA: Holmes & Narver Inc 1966.

[8] LI Q M, REID S R, AHMAD-ZAIDI A M.Critical impact energies for scabbing and perforation of concrete target[J].Nucl.Eng.Des., 2006, 236:1140-1148.

[9] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J].Int.J.Impact Eng., 1994, 15(4):395-405.

[10] FORRESTAL M J, FREW D J, HICKERSON J P, et al.Penetration of concrete targets with deceleration-time measurements[J].Int.J.Impact Eng., 2003, 28:479-497.

[11] FREW D J, HANCHAK S J, GREEN M L, et al.Penetration of concrete targets with ogive-nose steel rods[J].Int.J.Impact Eng., 1998, 21(6):489-497.

[12] LI Q M, CHEN X W.Dimensionless formulae for penetration depth of concrete target impacted by non-deformable projectile[J].Int.J.Impact Eng., 2003, 28:93-116.

[13] BEN-DOR G, DUBINSKY A, ELPERIN T.High-Speed penetration dynamics: engineering models and methods[M].Singapore: World Scientific, 2013.

[14] GAO Shiqiao, JIN Lei, LIU Haipeng, et al.A normal cavity-expansion(NCE) model based on the normal curve surface(NCS) coordinate system[J].International Journal of Applied Mathematics, 2007, 37(2):78-83.

[15] HOLMQUIST T J, JOHNSON G R.Response of silicon carbide to high velocity impact[J].Journal of Applied Physics, 2002, 91(9):5858-5866.

[16] GAO Shiqiao, LIU Haipeng, JIN Lei.A fuzzy model of the penetration resistance of concrete targets[J].Int.J.Impact Eng., 2009, 36: 644-649.

[17] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J].International Journal of Impact Engineering, 1994, 15(4):395-405.

[18] WARREN T L, FORRESTAL M J, RRANDLES P W.Evaluation of large amplitude deceleration data from projectile penetration into concrete targets[J].Experimental Mechanics, 2014, 54:241-253.

Real-time predicting penetration depth of projectiles into concrete targets based on acceleration measurement and fuzzy model

ZHANG Dongmei, GAO Shiqiao, LIU Haipeng, NIU Shaohua

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)

In order to predict the real-time penetration depth of all ogive-nose projectiles into concrete targets, a new method was developed based on the acceleration data measured in penetration tests with ogive-nose projectiles into semi-infinite concrete targets.With the proposed method, the whole penetration process was divided into three stages with instantaneous velocity, and each stage was described with different models.Through judging the calculation error, threshold velocities between stages were automatically determined.At the same time, the initial striking velocity of a penetration process was calculated by using the measured acceleration curve on the whole trajectory.It was shown that the predicted values with the proposed method are in reasonably good agreement with the measured data from tests.

penetration; concrete; fuzzy method; real-time prediction

2015-07-20 修改稿收到日期：2016-02-25

张冬梅 女 博士生1984年2月出生

高世桥 男,教授,博士生导师,1961年6月生

O385

A

10.13465/j.cnki.jvs.2017.05.028