高速旋转柔性梁刚柔耦合动力学分析

周兰伟, 陈国平, 孙东阳

(1.南京理工大学 机械工程学院，南京 210094;2.南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016;3.重庆大学 航空航天学院, 重庆 400044)

高速旋转柔性梁刚柔耦合动力学分析

周兰伟1, 陈国平2, 孙东阳3

(1.南京理工大学 机械工程学院，南京 210094;2.南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016;3.重庆大学 航空航天学院, 重庆 400044)

基于一次近似理论对绕纵轴高速旋转的柔性梁进行动力学分析，考虑了轴向与横向振动之间的耦合作用以及由偏心产生的离心力作用；采用Hamilton原理导出了旋转柔性梁在恒定转速下动力学方程，并采用假设模态法对所得动力学方程进行分析，得出恒定转速下柔性梁一次近似模型与零次近似模型动力学响应。二者对比表明柔性梁在低速旋转时刚柔耦合项影响较小，可以忽略，可采用零次近似模型；而在高速旋转时刚柔耦合项影响较大，不可以忽略，应采用一次近似模型以得到较为精确的结果。

高速； 旋转柔性梁； 一次近似； Hamilton原理;假设模态法

绕自身纵轴旋转梁是工业中应用极为广泛的一种基本机械元件，在航空领域、工业生产中都有着极为广泛的用途，如航空、航天等高科技领域内的旋转飞行器、卫星支撑臂及机械中的微型旋转部件等都可以用旋转梁来模拟其运动状态及动态特性。随着科学技术的发展及工作环境的变化，旋转结构的应用领域越来越广泛，如在飞行过程中需要较高的转速来保证飞行稳定性的高速旋转飞行器[1]、横轴旋翼机等；此外对旋转机构的旋转速度的要求也越来越高，相应地对于高速甚至超高速工作状态下部件的安全性、稳定性要求亦随之增高。因此此类柔性旋转结构动力学特性也受到越来越多研究者的关注。

旋转梁的动力学特性研究最早可追溯到20世纪60年代，DIMENTBER[2]采用经典Euler-Bernoulli梁模型推导出了简支条件下旋转梁的特征方程； SHEU[3]以Rayleigh梁为基础研究了不同边界条件下旋转梁的涡动速度、临界转速、模态阵型等动力学特性； SLOETJES[4]采用主动模态阻尼及主动模态平衡方法对柔性转轴的振动控制进行了研究； MAMANDI[5]研究了恒定转速下Timoshenko梁在三向力作用下的非线性动力学响应；国内大量学者也对此作了全新的研究工作，钱新等[6-7]研究了旋转Rayleigh梁在重力作用下的动态特性，通过理论分析和数值模拟研究了激励频率、陀螺效应、转动惯量、长细比对涡动频率、临界速度和模态振型的影响及旋转Rayleigh梁在不同边界条件下线性和非线性模型下不同的动力学特性。

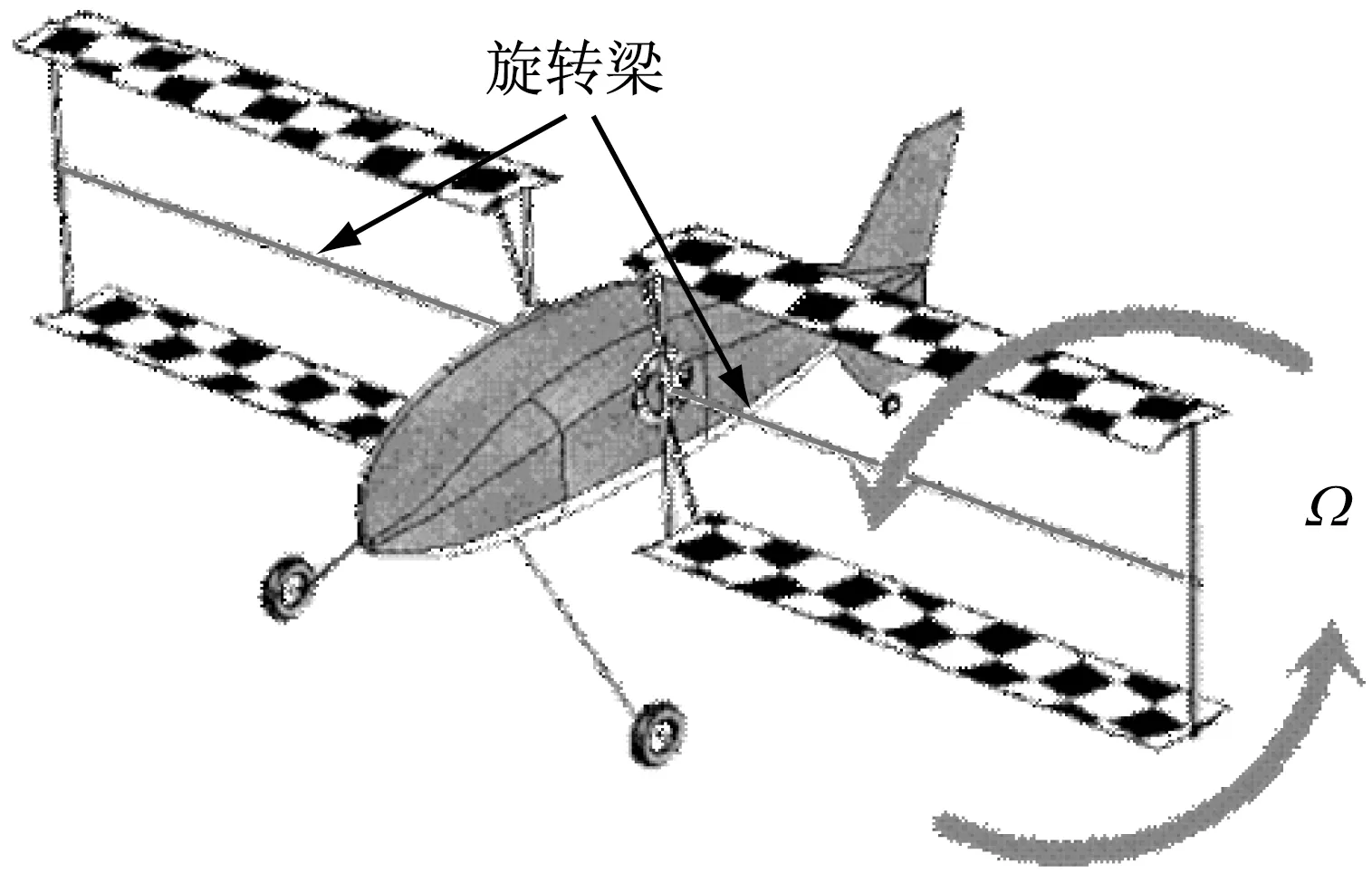
图1 横轴旋翼机中的旋转梁Fig.1 Spinning beam in cyclogyro

目前研究大都忽略了旋转梁的刚柔耦合项，在低速旋转情况下可以得到较为接近的结果，但是在高速旋转情况下采用此类分析方法所得到的结果往往与实际不符。在变形场描述中忽略由横向变形引起的轴向缩短效应的方法称为零次近似方法，反之，如果变形场描述中考虑这一项，则称之为一次近似方法[8]。一次近似方法在首先应用在以直升机旋翼为研究对象的旋转梁中，本文以横轴旋翼机中横轴为研究对象，如图1所示，采用一次近似Rayleigh梁模型对高速旋转柔性梁进行刚柔耦合动力学分析，采用广义Hamilton原理推导其动力学方程，并采用假设模态法分析相应的动力学响应，得到了不同转速下动力学响应并分别与零次近似模型进行了比较。

1 旋转柔性梁一次近似模型

高速旋转柔性梁，如图2所示，绕自身纵轴以恒定转速Ω旋转，梁长L，密度ρ，矩形截面。假设旋转时梁上某点的位移为D=uix+viy+wiz，则梁的实际轴向变化量根据连续介质力学原理[9]可写为

(1)

故D={s+wc}ix+viy+wiz

(2)

式(2)中积分项反映了由于横向变形引起的轴向缩短，将在变形场描述中忽略这一项的方法称为零次近似方法，反之，如果变形场描述中考虑这一项，则称之为一次近似方法。零次近似理论直接套用了结构动力学的小变形假设，忽略了此积分项，在低速情况下可以得到近似的结果，但是在高速旋转情况下可能导致错误的结论。

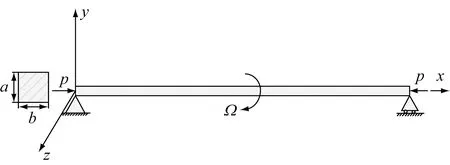
图2 旋转梁示意图Fig.2 Schematic diagram of spinning beam

通过将式(1)对x求导可得

(3)

根据Euler-Bernoulli梁假设，梁上任意一点的轴向正应变为

(4)

将式(3)代入式(4)得

(5)

2 旋转柔性梁动力学方程

旋转柔性梁的总动能可以由下式表示[5]T=Ts+Te，其中Ts和Te分别表示因转动和偏心引起的动能：

(6a)

(6b)

旋转梁势能可以写为

(7)

外力做功的变分为

(8)

式中：P表示梁两端所受轴力；Fx，Fy及Fz表示作用于旋转梁上的外力。

e(x)ρAΩ2cosθ1sin(Ωt+φ1(x))

(9a)

e(x)ρAΩ2cosθ2sin(Ωt+φ2(x))

(9b)

e(x)ρAΩ2cosθ3sin(Ωt+φ3(x))

(9c)

3 假设模态法

为了计算的简便，忽略了式9(a)～9(c)中部分变形耦合项wc及附加质量部分。旋转梁上任意一点轴向变形s及横向位移v,w可以写为

s(x,t)=Φs(x)qs(t)

(10a)

v(x,t)=Φv(x)qv(t)

(10b)

w(x,t)=Φw(x)qw(t)

(10c)

其中

Φsj(x)，Φvj(x)及Φwj(x)可以表示为[10-11]：

j=1,2,3,……n

(11)

将式10(a)～10(c)代入式9(a)～9(c)可得

Fxδ(x-l1)+e(x)ρAΩ2cosθ1sin(Ωt+φ1(x))

(12a)

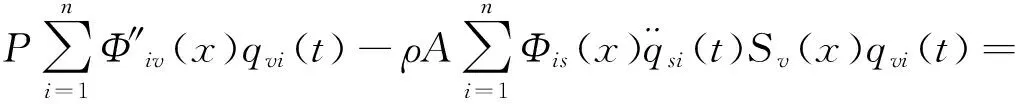
Fyδ(x-l2)+e(x)ρAΩ2cosθ2sin(Ωt+φ2(x))

(12b)

Fzδ(x-l3)+e(x)ρAΩ2cosθ3sin(Ωt+φ3(x))

(12c)

式12(a)～12(c)左右两边分别乘以Φsj(x)，Φvj(x)，Φwj(x)可得:

Fxχ(t)aj(x1)+ρAΩ2Κ1

(13a)

Fyχ(t)bj(x2)+ρAΩ2Κ2

(13b)

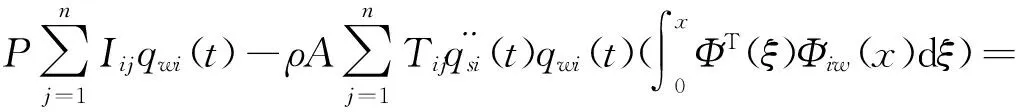
Fzχ(t)cj(x3)+ρAΩ2Κ3

(13c)

式中:Mij等可由Φsj(x)，Φvj(x)及Φwj(x)得到。其中：

式13(a)～13(c)经过简化可得：

(14a)

Fyχ(t)bj(x2)+ρAΩ2Κ2

(14b)

Fzχ(t)cj(x3)+ρAΩ2Κ3

(14c)

式中：aj(l1)=Φsj(l1)，bj(l2)=Φvj(l2)，cj(l3)=Φwj(l3)。

采用MATLAB中龙格-库塔法对上述方程进行数值分析，可分别得到qsj(t)、qvj(t)、qwj(t)，将其代入式10(a)～10(c)中即可得到高速旋转柔性梁的动力学响应。

4 算例分析

柔性梁的主要物理参数为：柔性梁的材料密度ρ为2 000 kg/m3，横截面积A为4×10-6m2，长度l为0.6 m，惯性矩Id为1.33×10-12m4，极惯性矩Ip为2.66×10-12m4，弹性模量E为1×1010N/m2，轴力P为0 N，假设偏心引起的三个方向的离心力载荷分别为

Fex=ρAΩ2K1=0.01ρAΩ2sin(Ωt+0.5π)，

Fey=ρAΩ2K2=0.005ρAΩ2sin(Ωt+0.1π)，

Fez=ρAΩ2K3=0.005ρAΩ2sin(Ωt+0.1π)。

所受外载荷方向及位置见图3

Fy=0.05sin(6πt)，Fx=Fz=0

为了考察零次近似与一次近似响应曲线，建立旋转柔性梁响应相似度：

(15a)

图3 旋转柔性梁加载示意图Fig.3 Load applied to spinning beam

(15b)

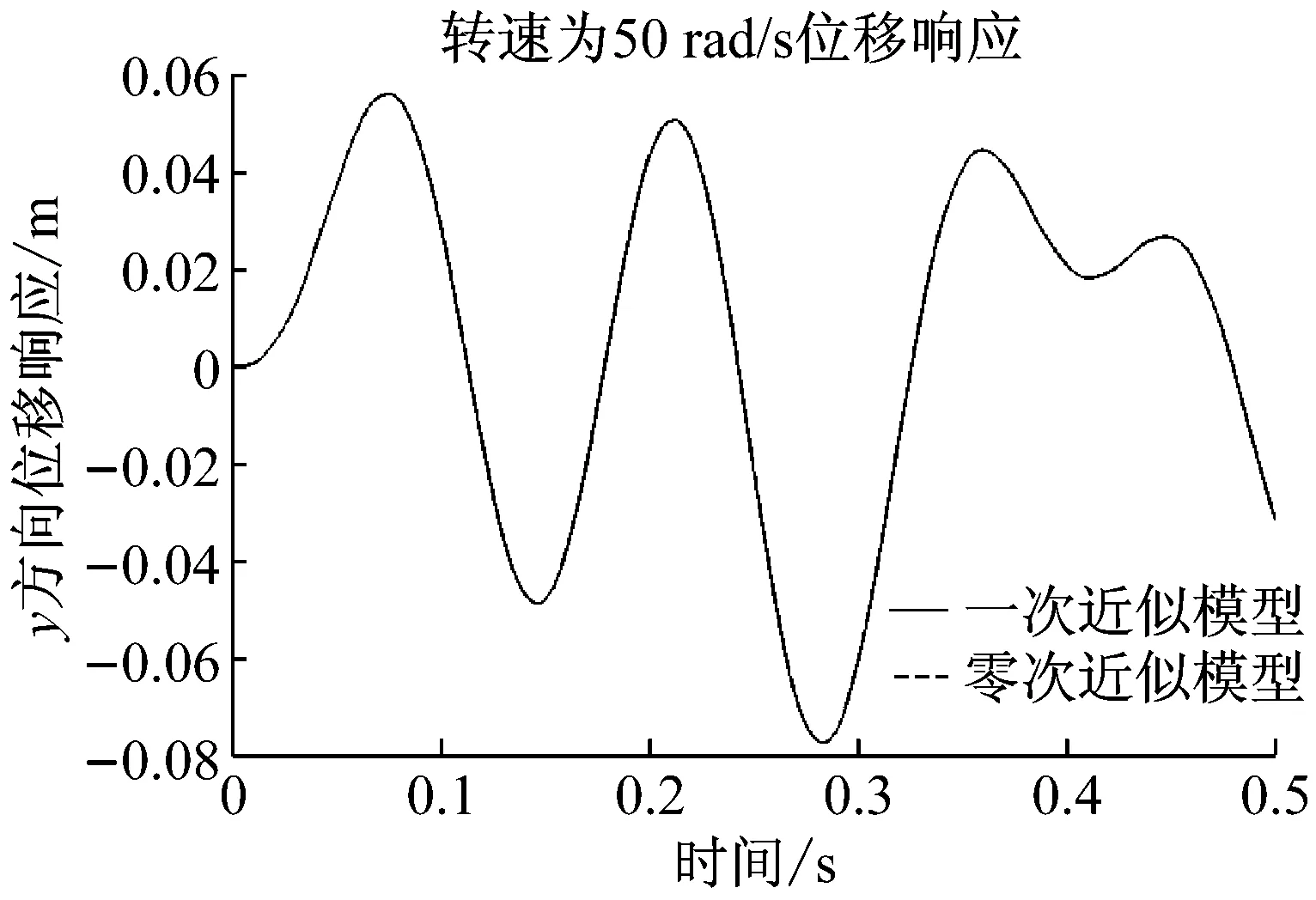
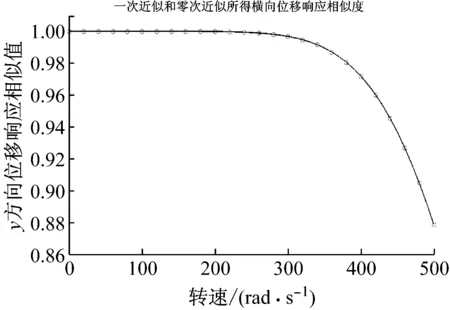
式中：v0，w0表示使用零次近似方法得到梁上某点的横向位移响应，v1，w1表示该点使用一阶近似方法得到的横向位移响应。当RV，RW为1时表示使用两种不同模型得到的横向位移响应完全相同，当值为0时表示横向位移响应完全不同。一次近似模型与零次近似模型所得到的位移响应曲线差异越大，则RV，RW越小。图4～图6分别表示不同转速下旋转柔性梁在离心力引起的载荷及外载荷作用下的横向位移曲线。从图4可以看出，在旋转速度为50 rad/s时一次近似模型与零次近似模型所得到的位移响应曲线差异较小，说明在低速旋转时刚柔耦合项对梁的动力学特性影响较小，可以忽略，此时采用零次近似模型即可较好地描述低速旋转柔性梁动力学特性；旋转速度为220 rad/s时两种模型得到的横向位移具有明显差异，如图5所示；图6表示在270 rad/s时，所得横向位移差别很大，说明零次模型此时已经不能准确描述旋转梁的动力学特征。从图7可以看出两种模型所得到的横向位移曲线的差异随着转速的增加逐渐增大，在480 rad/s时两种模型得到的位移相似度仅为0.9，说明高速旋转时刚柔耦合项对梁的动力学特性影响较大，不可以忽略，此时零次近似模型已不适用于高速旋转柔性梁的建模，而一次近似模型由于考虑了轴向位移对横向振动的影响，能更准确地描述高速旋转柔性梁动力学特性。

5 结 论

本文详细推导了基于一次近似模型绕纵轴高速旋转柔性梁的刚柔耦合动力学方程，并采用假设模态法对柔性梁动力学响应进行了分析。

算例结果表明，旋转柔性梁低速旋转时采用一次近似模型所得到的动力学特性与零次近似模型存在较小差异，而高速旋转时两种模型表现出较大差异，说明忽略了轴向变形对横向变形影响的零次近似模型不能准确地描述高速旋转柔性梁的动力学特性，而采用一次近似模型方法可以得到更为准确的结果。

[1] 朱怀亮.高速旋转飞行器弯—扭—轴向变形耦合与拍振[J].振动与冲击, 2002, 21(2): 32-35.

ZHU Huailiang.Dynamic analysis of sinning flexible missiles with coupled lateral-torsional-axial vibrations[J].Journal of Vibration and Shock, 2002, 21(2): 32-35.

[2] DIMENTBERG F M.Flexural vibrations of spinning shafts[Z].Butterworths Press, London, 1961.

[3] SHEU G J, YANG S M.Dynamic analysis of a spinning Rayleigh beam[J].International Journal of Mechanical Sciences, 2005, 47(2): 157-169.

[4] SLOETJES P J, DE BOER A.Vibration reduction and power generation with piezoceramic sheets mounted to a flexible shaft[J].Journal of Intelligent Material Systems and Structures, 2008, 19(1): 25-34.

[5] MAMANDI A, KARGARNOVIN M H.Nonlinear dynamic analysis of an axially loaded rotating Timoshenko beam with extensional condition included subjected to general type of force moving along the beam length[J].Journal of Vibration and Control, 2012,19(16):2448-2458.

[6] QIAN X, DU X.Dynamic characteristics of spinning Rayleigh beams[J].Lixue Xuebao/Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 635-640.

[7] FRANK PAI P F, QIAN X, DU X W.Modeling and dynamic characteristics of spinning Rayleigh beams[J].International Journal of Mechanical Sciences, 2013,68:291.

[8] 董兴建，孟光，蔡国平,等.旋转柔性梁的动力学建模及分析[J].振动工程学报, 2006, 19(4): 488-493.

DONG Xingjian, MENG Guang, CAI Guoping, et al.Dynamic model ling and analysis of a rotating flexible beam[J].Journal of Vibration Engineering, 2006, 19(4): 488-493.

[9] YOO H H, RYAN R R, SCOTT R A.Dynamics of flexible beams undergoing overall motions[J].Journal of Sound and Vibration, 1995, 181(2): 261-278.

[10] LEE H P.Dynamic response of a rotating Timoshenko shaft subject to axial forces and moving loads[J].Journal of Sound and Vibration, 1995, 181(1): 169-177.

[11] OUYANG Huangjiang, WANG Minjie.A dynamic model for a rotating beam subjected to axially moving forces[J].Journal of Sound and Vibration, 2007, 308(3): 674-682.

Rigid-flexible coupled dynamic analysis for a high-speed spinning flexible beam

ZHOU Lanwei1, CHEN Guoping2，SUN Dongyang3

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 210094;2.State Key Lab of Mechanics and Control of Mechanical Structures，Nanjing University of Aeronautics and Astronautics, Nanjing 210016，China;3.College of Aerospace Engineering，Chongqing University，Chongqing 400044, China)

Here, rigid-flexible coupled dynamic properties of a high-speed spinning flexible beam around its own longitudinal axis were studied.Using the first-order approximation model, the coupling effect of axial vibration and transverse one of the beam was considered.Besides, the centrifugal forces caused by eccentricity were also considered.The beam’s governing coupled partial differential equations of motion under a certain spinning speed were derived using Hamilton’s principle, and the assumed mode method was used for discretization.For different spinning, speeds, the transverse vibration response of the beam’s zero-order approximate model was compared with that of its first-order approximation model.The simulation results indicated that the zero-order approximate model is valid for the dynamic description of the flexible beam spinning at a lower speed since the effect of the rigid-flexible coupled terms is small and can be neglected; but when the beam spins at a higher speed, the first-order approximate model can account for the larger effect of the rigid-flexible coupled terms to obtain the beam’s more accurate dynamic response.

high-speed; spinning flexible beam; first-order approximation; Hamilton principle; assumed mode method

江苏高校优势学科建设工程资助项目(PAPD)

2015-10-19 修改稿收到日期：2016-02-21

周兰伟 男，博士生，1988年2月生，

陈国平 男，博士，教授，1956年7月生，E-mail：gpchen@nuaa.edu.cn

O327; O322

A

10.13465/j.cnki.jvs.2017.05.022