圆柱形长杆超高速正碰撞薄板结构破碎效应

汪庆桃，吴克刚，陈志阳

(国防科技大学 指挥军官基础教育学院，长沙 410073)

圆柱形长杆超高速正碰撞薄板结构破碎效应

汪庆桃，吴克刚，陈志阳

(国防科技大学 指挥军官基础教育学院，长沙 410073)

超高速碰撞多层板结构破碎效应研究对空间碎片防护及动能武器毁伤效应研究有着重要意义。采用ANSYS/AUTODYN程序的SPH方法，对超高速碰撞碎片云的形成过程进行了数值模拟，某典型时刻一次及二次碎片云形貌的数值模拟结果与实验结果吻合较好，验证了计算方法和模型参数的正确性。在此基础上采用数值模拟方法，对钨合金、轧制均质装甲(Rolled Homogeneous Armor，RHA)及LY12铝三种材料的圆柱形弹体超高速碰撞薄板的破碎规律进行了研究，基于量纲分析方法得出了弹体破碎长度随弹靶材料特性、弹靶尺寸及初始撞击速度变化的关系式。并研究了钨合金及RHA两种材料的长杆弹对八层RHA板结构的超高速碰撞效应。

超高速碰撞；SPH方法；圆柱形长杆弹；破碎规律

开展超高速碰撞研究最初最直接的需求来自航天器防护领域，目的是为了保护航天器在受到微流星体及空间碎片的撞击时不至于引起灾难性的失效。采用的方法是在航天器外一定距离处设置一块防护板[1]。近几十年来，随着防护技术、尤其是主动防护技术的发展，装甲战车、舰船、武装直升机及防护工程的抗打击能力越来越强，传统武器的毁伤效能受到了很大的制约，于是20世纪80年代世界各主要国家都倾注大量的人力与物力，探索研究对下世纪具有战略影响的各种新概念武器，最引人瞩目的要数动能武器(Kinetic Energy Weapon)。动能武器又称超高速动能导弹，其飞行速度可达二十几马赫数，是利用超高速飞行的弹头直接碰撞目标来达到摧毁的目的。关于超高速碰撞的研究，过去主要集中在球形低密度材料弹体的超高速碰撞的动力学响应方面，而关于圆柱形、大长径比、高密度材料弹体超高速碰撞的研究很少见诸报道。

MAIDEN[2]运用波传播理论对超高速弹体正撞击薄板时的破碎过程进行了定性描述。MAIDEN认为，弹靶材料的破碎是由于稀疏波引起材料中某一位置处的净拉伸应力超过材料的动态断裂强度而引起的。PIEKUTOWSKI[3-4]采用实验的方法研究了弹丸碰撞时发生破碎的临界撞击速度，并描述了碎片云的主要几何特征，包括外泡和内部结构，其中内部结构又分为前端、中心区、后部三部分。PIEKUTOWSKI[5]采用实验的方法研究了非球形弹丸超高速碰撞形成的碎片云形状。

本文针对圆柱形长杆超高速正碰撞薄板时的动力学问题，在对数值模拟方法进行验证的基础上采用数值模拟方法研究了超高速碰撞时长杆的应力状态、破碎过程及破碎特性，并研究了长杆对多层板结构的破坏效应。其研究结果对超高速碰撞毁伤评估具有一定的参考价值。

1 数值模拟方法及模型验证

超高速碰撞是一个典型的材料大变形、高温、高压及高应变率问题，弹体对多层板的超高速碰撞大致包括弹体撞击/侵彻前板阶段，弹体破碎、碎片云形成、扩展阶段，碎片云及剩余弹体撞击/侵彻后板阶段，以质点动力学为基础的数值模拟方法如SPH方法(Smoothed Particle Hydrodynamics)在描述这个过程存在着很大的优势[6-8]，得到了较为广泛的应用。

在进行数值模拟时，算法、材料模型及参数的选取会在很大程度上影响数值模拟结果的准确性和可信性，因此在进行数值模拟研究之前要根据实验结果对数值模拟方法及参数的正确性进行验证。由于钨合金和RHA材料的超高速撞击形成碎片云的相关实验数据从公开文献没有见到发表，所以本文首先验证算法，即先对铝材料超高速碰撞时碎片云形态的数值模拟结果与实验结果进行比较，通过结果的一致性说明数值模拟方法的准确性和可信性。关于材料方面，由于钨合金和RHA材料的动态本构关系及参数，研究成果相对较为成熟，可以直接参考，通过这种方法确定关于钨合金和RHA材料的超高速碰撞数值模拟结果的准确性和可信性。

在进行数值计算时，LY12铝的材料密度ρ为2.78 g/cm3，剪切模型G为27.8 GPa，采用TILLOSTON[9]状态方程、JOHNSON-COOK[10]本构模型。RHA的材料密度ρ为7.86 g/cm3，剪切模型G为77.3 GPa，钨合金的材料密度ρ为17.3 g/cm3，剪切模型G为145 GPa，这两种材料均采用SHOCK[9]状态方程、JOHNSON-COOK[10]本构模型。铝由于熔点及气点较低，在超高速碰撞中，会发生熔化甚至气化现象。在处理这类高压下的大变形及多相态共存问题时，用TILLOTSON[9]状态方程将会非常准确。TILLOTSON[9]状态方程是TILLOTSON(1962)和ALLEN(1967)提出来的，主要用来在大范围内精确描述金属材料在高速冲击下的响应问题。该状态方程适用的压力范围非常广，一般从0～103Mbar范围内的压力均能较好的应用。

如图1所示，Hugoniot曲线左边的区域属于等熵压缩区域；Ⅰ区表示的是材料的冲击压缩态；Ⅱ区表示的是材料冲击后的内能小于升华能(es)，材料经过等熵卸载后仍是固态，稍有膨胀；Ⅳ区表示的是材料的膨胀态，材料冲击后的内能足够大使其可以像气体一样膨胀；Ⅲ区是一个过渡区，其压力可通过Ⅱ区压力和Ⅳ区压力插值得到。

图1 Tillotson状态方程的P-V示意图Fig.1 Schematic diagram of P-V about the EOS of Tillotson

状态方程的具体表达式如下：

Ⅰ区(μ≥0)，其压力P1为

(1)

Ⅱ区(μ<0,e≤es)，其压力P2的表达式与P1的相同，只是B=0，具体表达式为

(2)

(3)

(4)

表1 LY12铝状态方程参数[11]Tab.1 Material parameters of EOS of aluminium[11]

JOHNSON-COOK本构模型是JOHNSON和COOK等[10]1983年提出的一个用于描述金属大变形、高应变率和高温情况下的经验型动态本构模型。由于该模型形式简单、使用方便、有着较高的精度，而且使用的变量在大多数计算程序中已经具备，所以该模型得到了广泛的应用。该模型把流动应力表示为

(5)

式中：A，B，C，n和m均为材料常数，由实验确定。三种材料的Johnson-Cook本构模型的具体参数见表2。

表2 材料的Johnson-Cook模型参数Tab.2 Material parameters of Johnson-Cook mode

钨合金的SHOCK状态方程参数[12]S、C0、γ分别为1.237、4 029 m/s、1.54。RHA的SHOCK状态方程参数[12]S、C0、γ分别为1.73、4 610 m/s、1.67。

此外，材料的失效模型及参数对于数值模拟结果的准确性影响也很大。本文对于上述几种材料均选取有效塑性应变失效模型，其值取2。

图2为直径为15.88 mm的LY12铝球以6.15 km/s的速度撞击0.772 mm铝板时的数值模拟结果与实验结果[13]的比较，数值模拟时弹靶材料均离散成SPH粒子，光滑半径为0.15 mm。从图2可以看出，弹丸在撞击靶板后8.1 μs和23.2 μs时刻时的数值模拟结果与实验结果吻合较好。

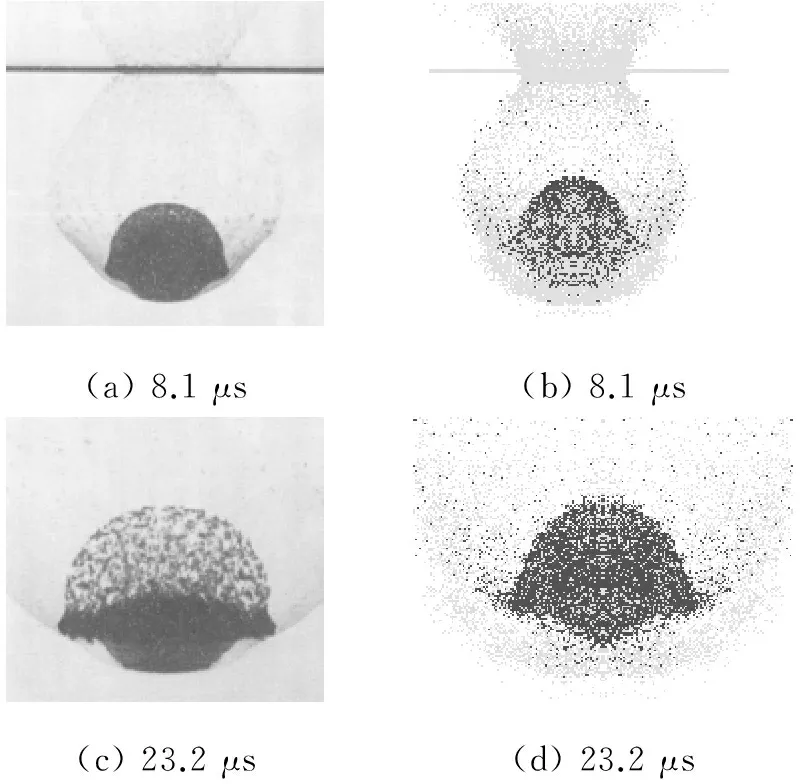
(a)8.1μs(b)8.1μs(c)23.2μs(d)23.2μs

图2 一次碎片云的数值模拟结果和实验结果[13]的比较

Fig.2 Simulation results and corresponding images[13]

图3为直径为3.99 mm、长径比为3的圆柱形锌弹体以4.97 km/s的速度垂直撞击0.965 mm厚的锌板时形成的碎片云形貌[14]。锌材料密度ρ为7.13 g/cm3，采用SHOCK状态方程，流体本构模型。SHOCK状态方程参数S、C0、γ分别为1.581、3 005 m/s、1.96。

13μs12.9μs

图3 一次碎片云的数值模拟结果和实验结果[14]的比较

Fig.3 Simulation results and corresponding images[14]

从上可以看出，本文所采用的数值模拟方法及材料参数能够正确描述碎片云形貌、扩展及与靶板相互作用规律，可以用其来进行相关的数值模拟研究。

2 圆柱形长杆正碰撞薄板时弹体的动态响应

2.1 弹靶变化过程

对长径比为10，半径为45 mm的圆柱形钨合金长杆超高速撞击15 mmRHA板时弹体中的应力状态进行数值模拟，由于整个模型严格对称，为了减小计算规模，节约计算时间，简化为二维轴对称模型，数值模拟初始图，如图4所示。

图4 数值模拟初始图Fig.4 The initiatory image of numerical simulation

图5为弹体以4 km/s的速度撞击靶板时不同时刻的压力云图，从图5可以看出，在撞击初始时刻，弹靶中产生峰值压力高达180 GPa的压缩波，并分别向弹靶中传播，同时，侧向系数波的传入使得靠近自由面处的压缩波峰值压力下降。当靶板中的压缩波在到达靶板背面的时候，反射成稀疏波，在靶板中产生拉应力，使得弹靶材料破碎，形成碎片云(如图5(c)所示)，同时，稀疏波通过弹靶接触界面，进入弹体，对弹中的波后状态进行卸载。弹中的压缩波在传播过程中峰值压力下降很快，在30 μs时为16 GPa，在50 μs时下降到约1.0 GPa。

为了跟踪记录超高速撞击时弹靶中的状态参量变化情况，设置了如图6所示的示踪点。图7为撞击速度为4 km/s时7～19号示踪点处的压力时间曲线，从图7可以进一步看出应力波在杆中的传播情况。

(a) 5 μs

(b) 10 μs

(c) 15 μs

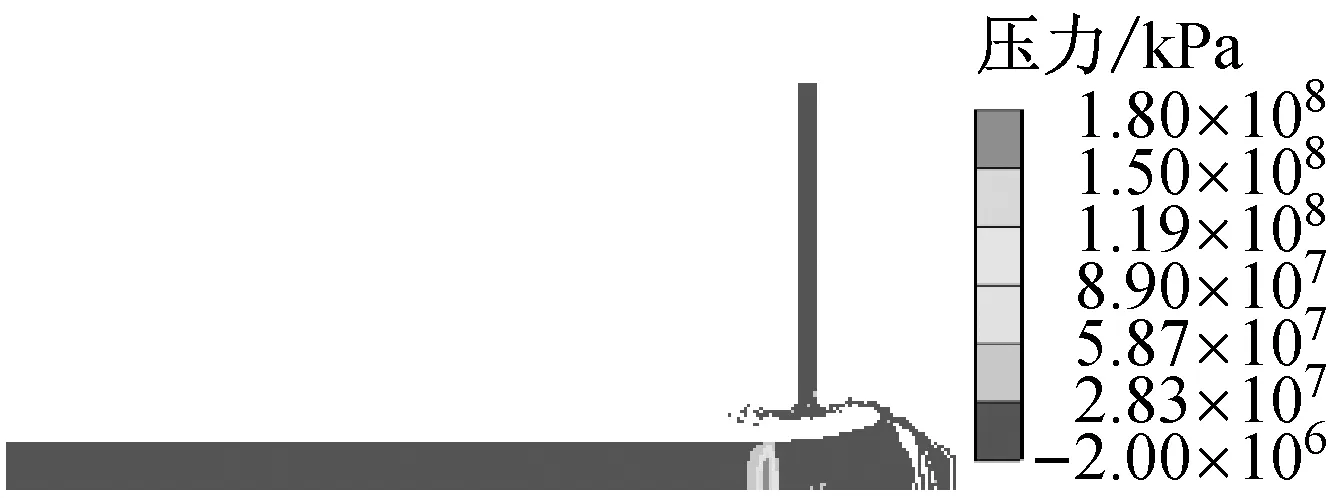
(d) 30 μs

(e) 50 μs

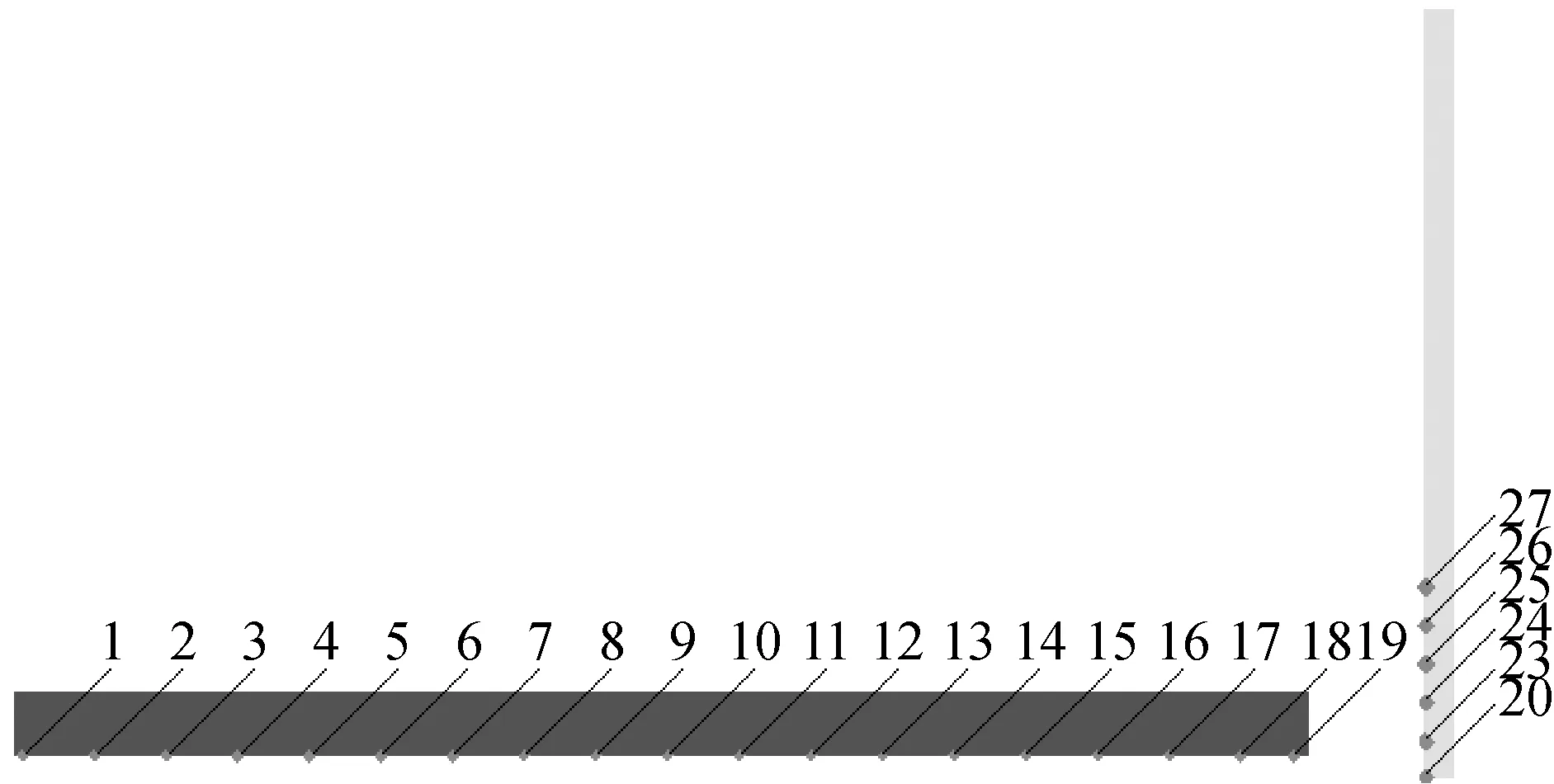
图6 示踪点设置位置示意图Fig.6 Schematic diagram of the position of tracing point

2.2 弹体的破碎规律

超高速碰撞过程中弹体的破碎机理非常复杂，现有的理论很难定量的描述超高速碰撞时弹体的破碎长度。数值模拟方法可以非常清晰的描述弹体超高速碰撞靶板时的破碎过程，并精确计算弹体的破碎长度。因此，通过设置不同的初始条件，就可以得出弹体的破碎长度与撞击参数、靶板尺寸及材料参数之间的关系。设计了如表3所示的工况。表3考虑了三种材料，每种材料对应四种不同的弹体几何尺寸，对每种工况进行数值计算，得出弹体在侵彻靶板过程中弹体的剩余长度。图8为钨合金、RHA及铝弹体以2～6 km/s的速度撞击靶板时侵蚀长度随撞击速度变化曲线(L1为侵蚀长度)。从图8可以看出，随着撞击速度的提高，对于钨合金、RHA及铝三种材料来说侵蚀长度随之增大；在速度相同时，随着(ts/dp)值的增大，侵蚀长度也相应增大，但是三种材料的增长率随ts/dp变化的情况是不相同的。图9为不同ts/dp值时不同材料侵蚀长度随撞击速度变化曲线。从图9(a)可以看出，在初始速度为2.0 km/s时，RHA和钨合金的侵蚀长度相差不大，而铝侵蚀长度较大；随着撞击速度的增大，RHA的侵蚀长度几乎呈线性增大，而钨合金的侵蚀长度相比RHA来说增大更为明显。在2～6 km的速度范围内，铝的侵蚀长度始终比钨合金及RHA大。

(a) 14～19号示踪点

(b) 7～13号示踪点

从上可以看出，弹体的破碎长度与弹靶的相对尺寸及材料特性相关。记破碎长度L1为F，本文的数值模拟包含了四个初始条件的变化(弹体直径dp，密度ρp，撞击速度Vp,0，靶板厚度ts1)，当分析初始条件对F的影响时，F为包含四个变量的函数。保持三个初始参数不变，只考虑第四个初始参数变化对F的影响，往往较容易得到F随该初始参数变化的规律。

表3 数值模拟工况Tab.3 Numerical simulation conditions

为了得到经验关系式的可能形式，考虑在初始参数变化下F的变化，考虑材料的可压缩性，引进声速C，忽略材料强度、熔化和气化效应，则有：

F=F(Vp,0,dp,ρp,Cp,ts1,ρt,1,Ct,1)

(6)

选择第一层靶板密度ρt,1、靶板材料声速Ct,1及弹体直径dp作为基本量进行无量纲化，有：

(7)

借鉴DEPCZUK[15]的分析，假定F的形式为

(8)

式中：ki(i=0，1，2，3，4)为待定参数。则有下列关系式：

(9)

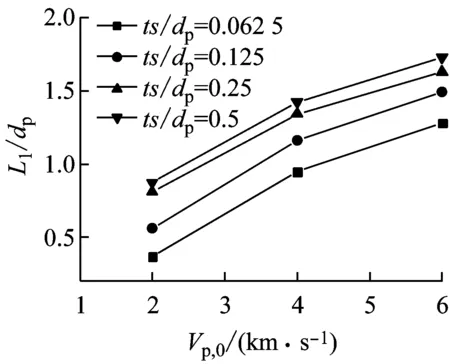
(a) 钨合金

(b) RHA

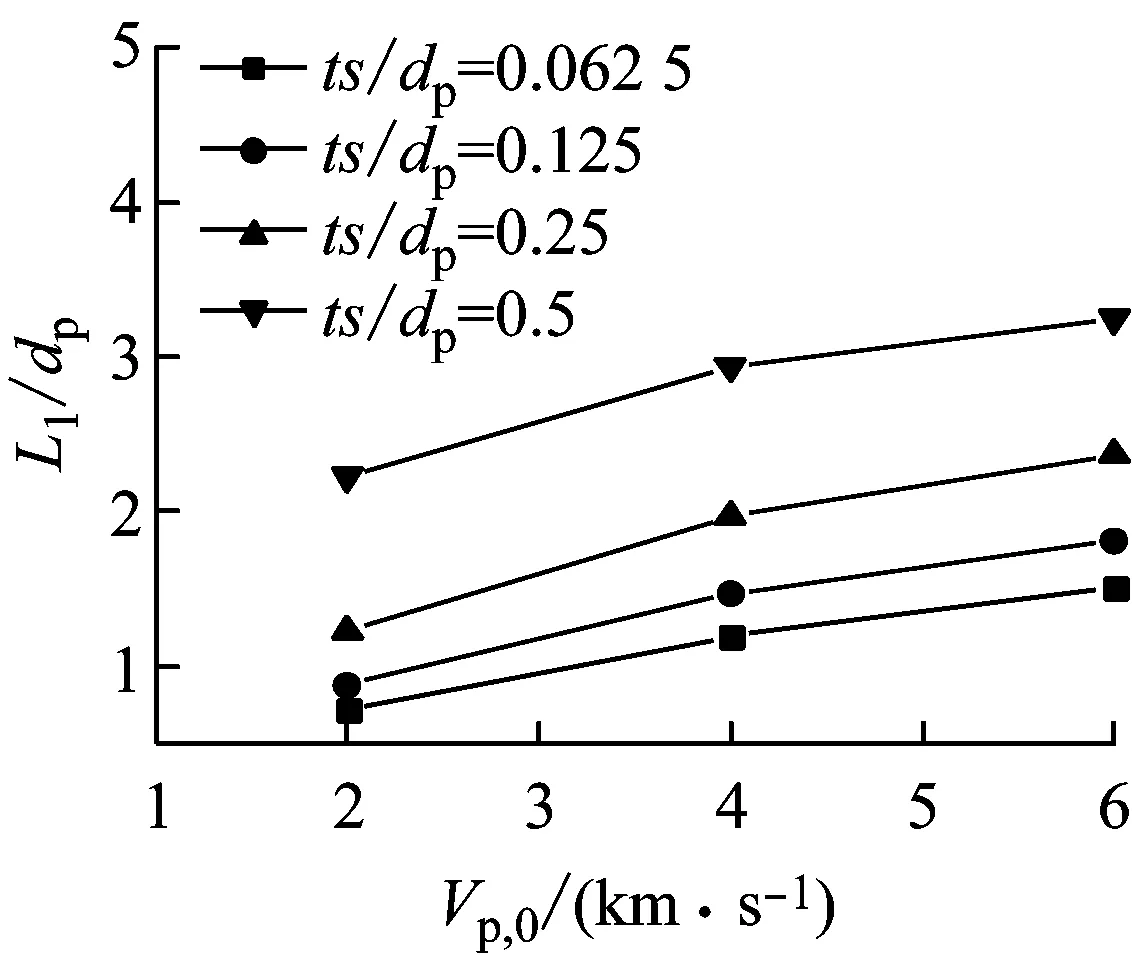
(c) 铝

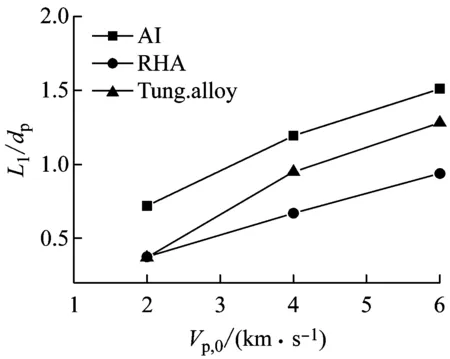
(a) ts/dp=0.062 5

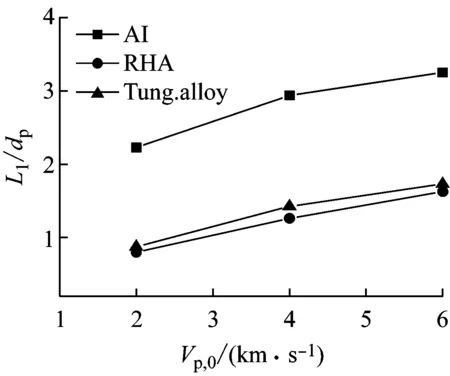
(b) ts/dp=0.5

对数值计算的数据进行拟合，得到大长径比圆柱形弹体超高速碰撞靶板时破碎长度的经验公式为

(10)

从公式(10)可以看出，大长径比圆柱形弹体超高速撞击靶板时的破碎长度与弹体的初始撞击速度及靶板厚度成正比，与弹体的密度及声速成反比。

3 圆柱形长杆正碰撞多层板结构效应

圆柱形长杆弹对多层板结构的侵彻与侵彻单层板有着明显不同，当弹体超高速碰撞前一层板时，弹靶材料会发生破碎，形成碎片云，碎片云由外泡结构和剩余的弹体组成，对下一层靶板的作用要分别考虑碎片云的作用与剩余弹体的作用。现在考虑一八层板结构，靶板材料为RHA，每层板的间隔均为2 500 mm，第一层厚度为70 mm、第三层为40 mm、其余板厚度为15 mm。弹体为重100 kg的圆柱形钨合金、RHA材料弹体，长径比为10。采用数值拟的方法分别计算弹体以4 km/s、6 km/s的速度撞击多层板结构时弹体的响应及多层板结构的破坏情况。

图10为钨合金弹以4 km/s的速度撞击多层板结构时的质量随时间变化情况，从图10可以看出，弹体可以完全穿透多层板结构。当弹体穿过第一层板之后弹体剩余质量为88.3 kg；通过第二层板之后剩余质量为84.9 kg；通过第八层板之后剩余弹体的质量50.1 kg。从图10还可以看出，弹体穿过相同及不同厚度的靶板时侵蚀的质量均不一样，总体来看，前面一层靶板越厚，在侵彻下一层靶板时弹体的侵蚀质量少。分析原因为，当前一层靶板较厚时，弹体在侵彻过程中形成的碎片云质量越大，动能也越大，所以碎片云对穿透后一层靶板的贡献越大，故弹体侵蚀的质量相对就越少。图10为相同情况下弹体剩余速度随时间的变化曲线，从图10可以看出，弹体通过八层板之后弹体的剩余速度为3.89 km/s，仅减少了2.7%。

图10 钨合金弹以4 km/s的速度碰撞多层板结构时剩余质量随时间变化曲线Fig.10 Curve of residual velocity versus time of the projectile impact at 4 km/s

图11 钨合金弹以4 km/s的速度碰撞多层板结构时剩余速度随时间变化曲线Fig.11 Curve of residual velocity versus time of the projectile impact at 4 km/s

当钨合金弹体以6 km/s的速度撞击多层板结构时，弹体通过第八层板时剩余质量为33.0 kg。这说明随着弹体初始速度的增加，弹体通过八层板之后剩余质量明显减小，这可能是随着初始撞击速度的增加，碰撞产生的应力增大，导致弹体破碎更加严重。而通过八层板之后的剩余速度为5.93 km/s，减小1.2%。而对于长径比为10的RHA弹以4 km/s的速度碰撞多层板结构时，也能完全穿透多层板结构，剩余质量为55.1 kg，减少44.9%；剩余速度为3.84 km/s，减少4.0%；当速度增加到6 km/s时，剩余弹体质量及速度分别为35.0 kg及5.80 km/s，分别减少65%和3.3%。从上可以看出，圆柱形弹体在每穿透一层靶板之后，都会发生一定长度的破碎，损失一定的质量，且当靶板厚度越大时，弹体侵蚀的质量越大。

4 结 论

圆柱形长杆弹超高速碰撞破坏效应研究对空间碎片防护及动能武器毁伤效应研究有着重要意义。本文采用ANSYS/AUTODYN程序，对不同材料的圆柱形长杆弹超高速碰撞薄板进行了数值模拟研究，得出了钨合金、RHA及铝三种材料的圆柱形长杆弹超高速碰撞时弹体质量变化规律，基于量纲分析的方法得出了弹体侵蚀长度随弹靶材料特性、弹靶几何尺寸及初始撞击速度变化的关系式。并研究了钨合金及RHA两种材料的长杆弹对八层RHA板结构的超高速碰撞效应，得出了该条件下撞击速度在4 km/s～6 km/s速度范围内时弹体速度变化很小、弹体质量侵蚀随撞击速度增大而增大的变化规律。本文的研究成果对弹体设计、超高速碰撞毁伤评估具有一定的参考价值。

[1] WHIPPLE F L.Meteorites and space travel[J].Astronomical Journal, 1947，1161：131.

[2] MAIDEN C J，MCMILLAN A R.An investigation of the protection afforded a spacecraft by a thin shield[J].AIAA Journal，1964：1992-1998.

[3] PIEKUTOWSKI A J.Characteristics of debris clouds produced by hypervelocity impact of aluminum spheres with thin aluminum plates[J].Int.J.Impact Eng., 1993，14:573-86.

[4] PIEKUTOWSKI A J.Fragmentation-initiation threshold for spheres impacting at hypervelocity[J].Int.J.Engng, 2003, 29: 563-574.

[5] PIEKUTOWSKI A J.Debris clouds produced by the hypervelocity impact of nonspherical projectiles[J].Int.J.Impact Eng., 2001，26: 613-624.

[6] LUCY L B.A numerical approach to the testing of the fission hypothesis[J].Astron.J., 1977，82：1013.

[7] 汪庆桃，张庆明，吴克刚，等.超高速碰撞形成一次碎片云特性研究[J].国防科技大学学报, 2013, 35(5):124-128.

WANG Qingtao, ZHANG Qingming, WU Kegang, et al.Description of the first debris clouds formed by hypervelocity impact[J].Journal of National University of Defence Technology, 2013, 35(5):124-128.

[8] 汪庆桃，张庆明.多层板结构超高速碰撞效应的数值模拟[J].兵工学报,2012，33:227-230.

WANG Qingtao，ZHANG Qingming.Simulation for damage effect about multi-plate structure impact by hypervelocity projectil[J].Acta Armamentar Ⅱ, 2012,33:227-230.

[9] ANSYS AUTODYN 14.0.Theory manual, ANSYS Inc.Pittsburgh.

[10] JOHNSON G R, COOK W H.A constitutive model and data for metals subjected to large strains, high strain rates, and high temperatures[C]//Proceedings of the 17th International Symposium on Ballistics.Holland,[s.n.], 1983：541-547.

[11] HIERMAIER S, KONKE D, STILP A J, et al.Computational simulation of the hypervelocity impact of Al-spheres on thin plates of different materials[J].Int.J.Impact Engng., 1997，20: 363-374.

[12] 汪庆桃.多层等效结构的超高速碰撞效应[D].北京: 北京理工大学: 2010.

[13] PIEKUTOWSKI A J.Characteristics of debris clouds produced by hypervelocity impact of aluminum spheres with thin aluminum plates[J].Int.J.Impact Eng., 1993,14:573-586.

[14] BEISSEL S R, GERLACH C A, JOHNSON G R.Hypervelocity impact computations with finite elements and meshfree particles[J].Int.J.Impact Engng, 2006，33：80-90.

[15] DEPCZUK D, SCHONBERG W P.Characterizing debris clouds created in oblique orbital debris particle impact[J].Journal of Aerospace Engineering, 2003，16(4)：177-190.

Fragmentation effect of a long cylindrical rod with a hypervelocity normaly impacting a thin plate structure

WANG Qingtao, WU Kegang, CHEN Zhiyang

(College of Basic Education, National University of Defense Technology, Changsha 410073, China)

To study fragmentation effect of a cylindrical projectile with a hypervelocity impacting a thin plate structure is of great significance for space debris protection and kinetic energy weapons damage effect.Here, the debris cloud forming process and expanding were studied with the SPH method of ANSYS/AUTODYN code.It was shown that the numerical simulation results for the first and the secondary debris cloud morphologies are in good agreement with the test results, and the correctness of the calculation method and the model parameters was verified.Furthermore, the fragmentation laws of cylidrical projectiles made by 3 materials of tungsten alloys, RHA and LY12 aluminum with a hypervelocity impacting a thin plate structure were studied with the numerical simulation method.The empirical equations relating the fragment length of projectiles to target material properties, target size and inital impacting velocity are obtained with the dimensional analysis method.

hypervelocity impact; SPH method; long cylindrical rod; fragment law

国家部委资助项目(404030203)

2015-10-22 修改稿收到日期：2016-02-18

汪庆桃 男，博士，副教授，1978年生

V414.9

A

10.13465/j.cnki.jvs.2017.05.009