一类四维李代数的Rota-Baxter算子

范素军， 赵瑞斌， 关 玥， 吴艳茹， 王敏彦

(1.河北医科大学 数学教研室 河北 石家庄 050017； 2.河北医科大学 物理教研室河北 石家庄 050017； 3.河北医科大学 基础医学院 河北 石家庄 050017)

一类四维李代数的Rota-Baxter算子

范素军1， 赵瑞斌2， 关 玥3， 吴艳茹2， 王敏彦1

(1.河北医科大学 数学教研室 河北 石家庄 050017； 2.河北医科大学 物理教研室河北 石家庄 050017； 3.河北医科大学 基础医学院 河北 石家庄 050017)

随着李代数及相关代数理论的发展，Rota-Baxter算子在数学物理中得到广泛应用.给出了复数域上导代数维数等于一的四维李代数的分类，对得到的每一类李代数的权为零的Rota-Baxter算子结构进行了研究，给出了权为零的Rota-Baxter算子的完全分类，并给出了每一个Rota-Baxter算子的具体表示.

李代数； Rota-Baxter算子； 导代数

0 引言

可解李代数的结构在李代数的结构研究中起着非常重要的作用[1-3]，随着李代数理论的不断发展和完善，其理论与方法已逐步渗透到数学物理的许多领域.文献[4]研究了Rota-Bater李代数在理论物理上的应用.文献[5]给出了导代数维数等于一的二维和三维李代数，且权为零的Rota-Baxter算子的具体表达式,并通过Rota-Baxter算子的可逆性讨论了李代数的幂零性.李代数的Rota-Baxter算子与经典的Yang-Baxter方程的解从另一方面反映出李代数的代数结构[5-8].近几年Rota-Baxter代数在Yang-Baxter方程、Hopf代数、微分代数、量子域理论等方面也得到很好的应用[9-12].本文研究复数域上导代数维数等于一的四维可解李代数的权为零的Rota-Baxter算子的结构.

设L是域F上的线性空间，如果在L上存在斜对称的二元线性运算: [,]:L×L→L，满足对任意x,y,z∈L,[x,[y,z]]=[[x,y],z]+[y,[x,z]]，则称L是域F上的李代数.L的由所有[x,y]生成的子代数，称为李代数L的导代数，记为L1.对每个自然数s，记L(s+1)=[L(s),L(s)]，如果存在自然数s，使得L(s)=0，则称L是可解的李代数.显然，如果L是导代数维数等于一的李代数，则L是可解李代数.设L是域F上的李代数，λ∈F，如果线性变换P:L→L满足下列等式，则称P为李代数L的权为λ的Rota-Baxter算子.对任意x,y∈L,

[P(x),P(y)]=P([P(x),y]+[x,P(y)])+λP[x,y].

(1)

如果λ=0，则称P为李代数L的权为零的Rota-Baxter算子，以下简称P为李代数L的Rota-Baxter算子.

命题1 线性变换P:L→L为李代数L的权为零的Rota-Baxter算子的充要条件是，P/α为李代数L的权为零Rota-Baxter算子，其中α为域F中任意非零的数.

证明 由等式(1)知，λ=0时，P为李代数L的权为零的Rota-Baxter算子的充要条件是，[P(x),P(y)]=P([P(x),y]+[x,P(y)])成立.显然，此等式成立的充要条件是，两边都乘以非零数k,等式仍然成立.

1 主要结论

在本文中，主要讨论复数域C上的李代数.

引理1[7]设L是复数域C上导代数维数等于一的李代数，x1,x2,x3,x4是L的一组基,则在同构的意义下仅有下面3类：

为了讨论李代数L的Rota-Baxter算子，首先引入下面一些符号.设P:L→L是权为零的Rota-Baxter算子,P在基x1,x2,x3,x4表示为

(2)

定理1 设L是引理1中的四维李代数L1,设P:L→L是线性变换，P是L的权为零的Rota-Baxter算子的充要条件是P=0或P在基x1,x2,x3,x4下的矩阵为下列情形之一：

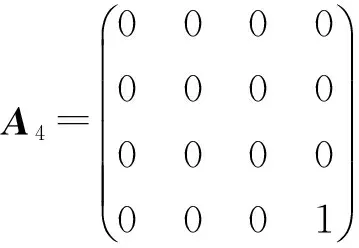
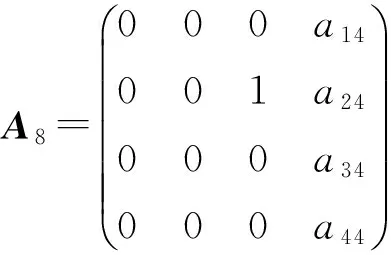
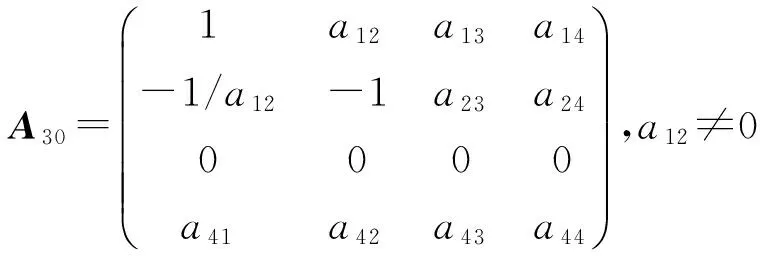
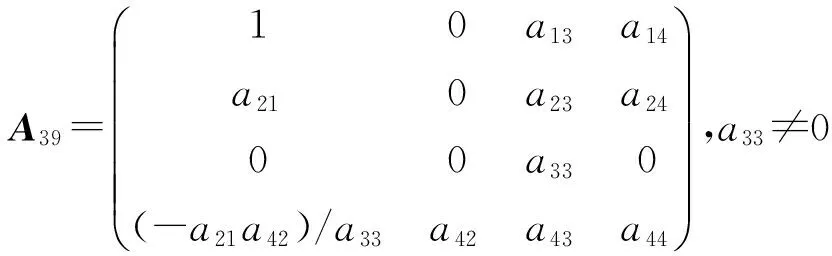
证明 设L是李代数L1，P:L→L是权为零的Rota-Baxter算子，P在基x1,x2,x3,x4的表示为等式(2). 显然，P=0是Rota-Baxter算子. 如果P≠0，由权为零的Rota-Baxter算子的定义、等式(1)及L1的乘法表可得:a21a42-a22a41=-a41a33；a11a42-a12a41=a42a33；(a11+a22)a33=a11a22-a12a21；(a11+a22)a34=0；a31=a32=0；a42a34=a41a34=0.下面分几种情形进行讨论.

1) 当a11+a22=0 时，得到a11a22-a12a21=0,如果a11=0，则a22=0， 所以，a12a21=0. 如果a34≠0，得到a42=a41=0，再由命题1，可得矩阵A1,A2,A3. 如果a34=0，得到a12a21=0，a41a42a33=0，分别讨论各种情形可得到矩阵A4,…,A28.如果a11≠0，由命题1，可以徦设a11=1，则a22=-1，a12a21=-1.如果a34≠0，得到a42=a41=0，得到A29. 如果a34=0, 得到矩阵A30,A31.

2) 当a11+a22≠0 时，则a31=a32=a34=0.如果a11=0，则a22≠0，不妨设a22=1. 如果a33=0，得到a12a21=0,a41=a21a42, 得到矩阵A32,A33,A34. 如果a33≠0，得到a12a21=a33且a41=a42=0,得到矩阵A35.如果a11≠0，不妨设a11=1, 则a22≠-1，在a33=0的情形下，得到a12a21=a22,可得到矩阵A36,A37.在a33≠0的情形下，得到a12a21=-a33(1+a22)+a22.如果a12=0，得到a22=0,a42=a41=0， 或是a41=-a21a42/a33,a42≠0,a33≠0, 分别得到矩阵A38,A39.如果a12≠0, 得到等价方程:a21a42-a22a41=-a41a33;a42-a12a41=a42a33;(1+a22)a33=a22-a12a21.如果a22=a33，则a41=a42=0，得到矩阵A40. 如果a22≠a33，由上述方程组进行讨论可知a41=a42=0，得到矩阵A41.证毕.

定理2 设L是引理1中的四维李代数L2,设P:L→L是线性变换，P是L的权为零的Rota-Baxter算子的充要条件是,P在基x1,x2,x3,x4下的矩阵为下列情形之一:

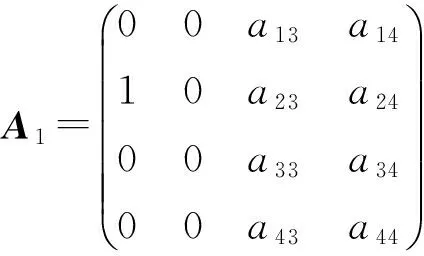
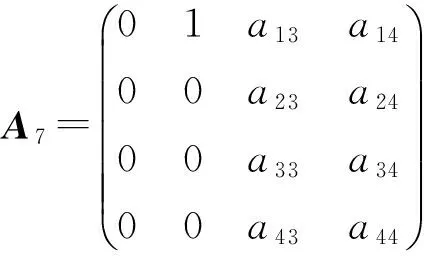
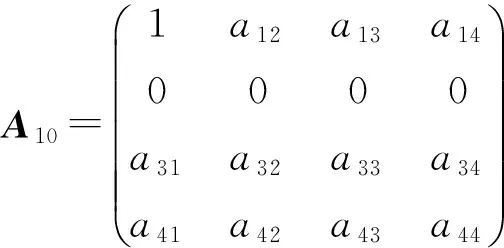
证明 由权为零的Rota-Baxter算子的定义及引理1可知， 当L是李代数L2时， 设P:L→L是权为零的Rota-Baxter算子. 由等式(1)、(2)及L1的乘法表得到下列关系同时成立:

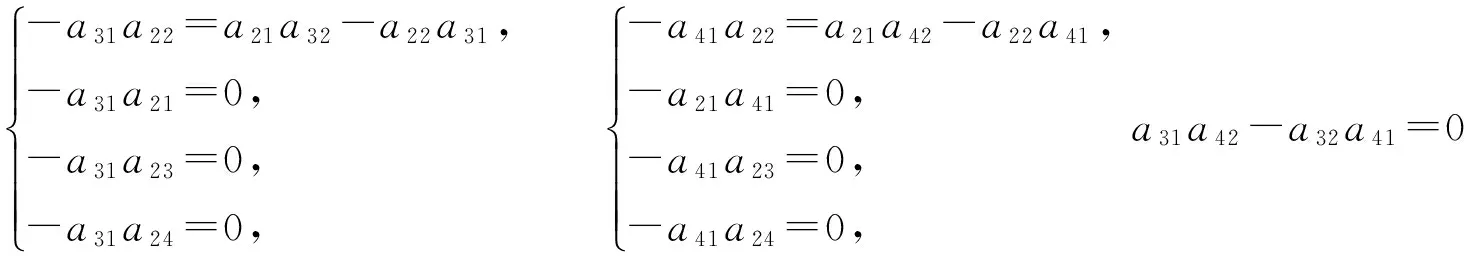
与定理1的证明方法类似，分几种情形进行讨论.

1)a11+a22=0 时，得到a11a22-a12a21=0.如果a22=0，则a11=0 ，a12a21=0,a12a31=a32a23=a32a24=0,a12a41=a23a41=a41a24=a42a23=a42a24=a23a31=a31a24=0, 分别讨论各种情况可得到矩阵A1,…,A8.如果a22≠0，由命题1，不妨设a22=1,则a11=-1.上述讨论可知a12a21=1.再由上面的方程组可得到矩阵A9.

2) 当a11+a22≠0 时，a21=a23=a24=0,得到(a11+a22)a22=a11a22，所以a22=0,得到矩阵A10. 证毕.

定理3 设L是引理1中的四维李代数L3,P:L→L是线性变换，P是L的权为零的Rota-Baxter算子的充要条件是，P在基x1,x2,x3,x4下的矩阵为下列情形之一：

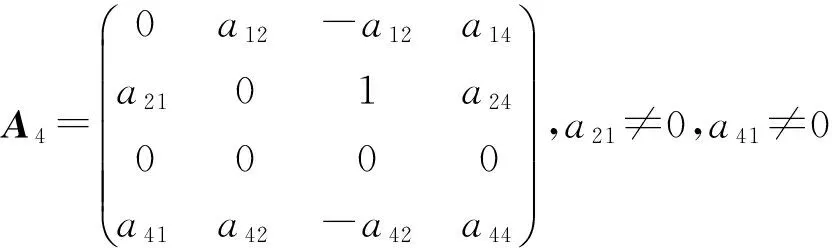
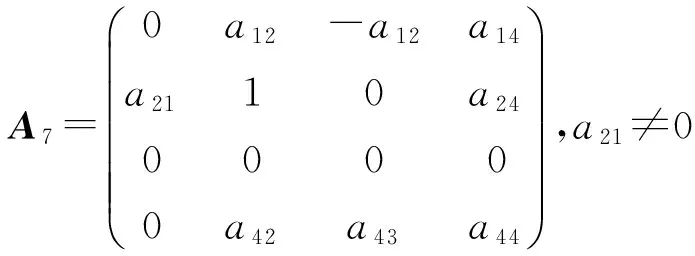
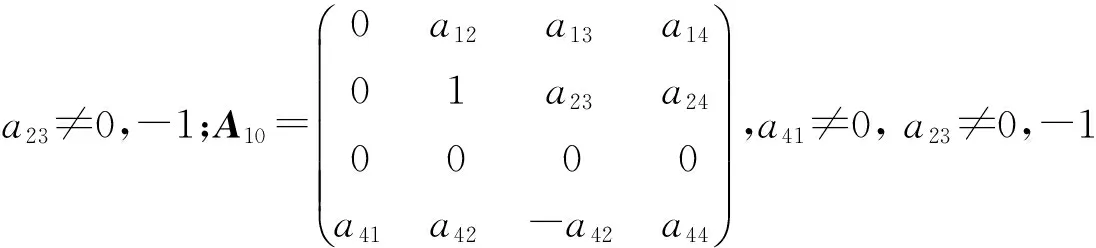
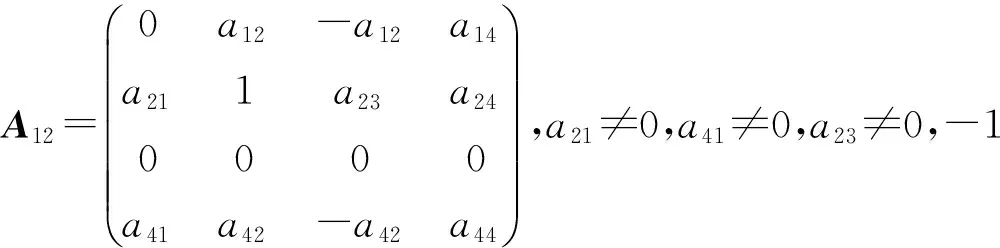
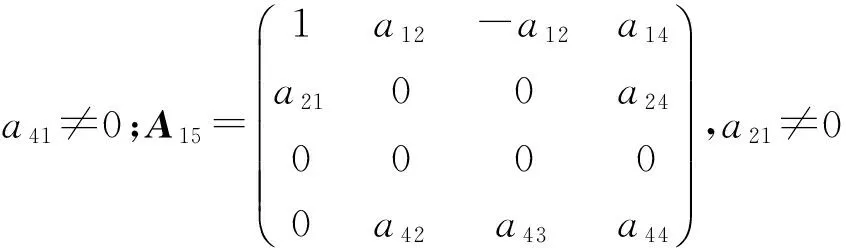
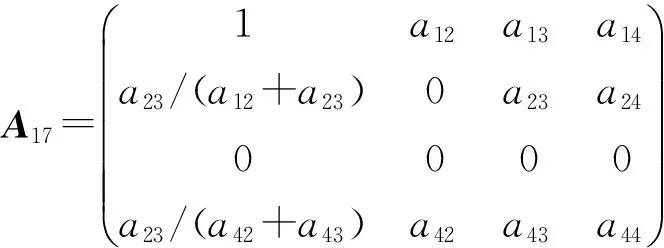
a22≠-1,a12≠-a13,a42≠-a43；

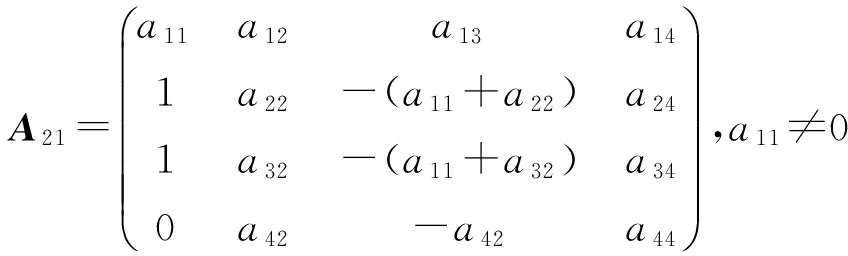
证明 设P:L→L是权为零的Rota-Baxter算子， 由权为零的Rota-Baxter算子的定义及引理1可知， 当L是李代数L3时， 由等式(1)、(2)及L1的乘法表得到下列关于系数的方程组：

分几种情形进行讨论.

1)a11+a22+a23≠0 时，得到a31=a32=a34=a33=0. 且由a11∶(a12+a13)=a21∶(a22+a23)=a41∶(a42+a43), 得到矩阵A1,…,A19.

2)a11+a22+a23=0 时，若a11+a32+a33≠0，仍可得矩阵A1,…,A19.如果a11+a32+a33=0，a31≠0，得到a41=0,a21=a31，a42+a43=0，且有a11a32-a12a31+a11a33-a13a31=a11a22-a12a21+a11a23-a13a21=0.可得矩阵A20,A21. 当a31=0时，得到a11=0，所以，a22+a23=0,a32+a33=0. 在a32≠0时，由命题1，得到a41=a21=0，a42=-a43, 得到矩阵A22. 在a32=0时，得到a33=0, 得到矩阵A23,A24,A25. 证毕.

[1] HUMPHREYS J E. Introduction to lie algebras and representation theory[M]. New York: Springer-verlag, 1972.

[2] MUBARAKZJANOV G M.Classification of solvable lie algebras of sixth order with a non-nilpotent basis element[J]. Izv Vyssh Ucebn Zaved Mat,1963,35(4):104-116.

[3] PATERA J, ZASSENHAUS H. Solvable lie algebras of dimension ≤4 over perfect fields[J].Linear algebra and its application, 1990,142(1): 1-17.

[4] MAKHLOUF A,YAU D.Rota-Baxter Hom-Lie-admissible algebras[J].Communications in algebra,2014,42(3):1231-1257.

[5] 范素军，刘冬艳，吴艳茹,等.李代数的Rota-Baxter算子[J].河北师范大学学报(自然科学版)，2014,38(6)：541-544.

[6] PEI J,BAI C M,GUO L. Rota-Baxter operators on sl(2,C) and solutions of the classical Yang-Baxter equation[J].Journal of mathematical physics,2014,55(2):368-378.

[7] BAI C M .A unified algebraic approach to the classical Yang-baxter equation[J].Journal of physics a-mathematical and theoretical, 2007,40(36):11073-11082.

[8] DRINFEL’D V G.Quantum groups[C]//Proceedings of the International Congress of Mathematicians.California:Berkeley,1986.

[9] GUO L.What is a Rota-Baxter algebra[J].Notices of the American mathematical society,2009,56(11):1436-1437.

[10]EBRAHIMI-FARD K, GUO Li. Free Rota-Baxter algebras and rooted trees[J]. Journal of algebra and its applications, 2008,7(2):167-194.

[11]EBRAHIMI-FARD K, GUO Li.Rota-Baxter algebras and dendriform algebras[J]. Journal of pure applied algebra, 2008,212(2): 320-339.

[12]EBRAHIMI-FARD K, GUO Li.Rota-Baxter algebras in renormalization of perturbative quantum field theory[J]. Fields institute communications,2007,50: 47-105.

ofPhysics,HebeiMedicalUniversity，Shijiazhuang050017,China; 3.CollegeofBasicMedical,

HebeiMedicalUniversity,Shijiazhuang050017,China)

(责任编辑：方惠敏)

Rota-Baxter Operators on a Class of 4-dimensional Solvable Lie Algebras

FAN Sujun1, ZHAO Ruibin2, GUAN Yue3, WU Yanru2, WANG Minyan1

(1.DepartmentofMedicalMathematics,HebeiMedicalUniversity，Shijiazhuang050017,China; 2.Department

With the development of Lie algebra and related algebra theory, Rota-Baxter operator was widely used in mathematics and physics. The classification of 4-dimensional Lie algebra with one-dimensional derived algebra over the complex number field was given, and the completely classification of Rota-Baxter operators with weight zero on the Lie algebra was also given, and the concrete expression of each Rota-Baxter operators of weight zero was provided as well.

Lie algebra; Rota-Baxter operator; derived algebra

2016-08-22

河北省自然科学基金项目(A2010000194)；河北省教育厅科学研究计划项目(Z2015010).

范素军(1981—)，女，河北石家庄人，讲师，主要从事应用数学、代数学和统计学研究,E-mail:fanny7138@163.com.

O152.5

A

1671-6841(2017)01-0011-06

10.13705/j.issn.1671-6841.2016207