利用图形表征解决数学问题的策略探析
2017-04-05余禄秀
余禄秀
(浙江省宁波市奉化区锦溪小学,宁波315000)
【摘 要】在校本研修活动中,笔者执教了《求比一个数多几的数》,通过多次磨课,笔者体会到低段利用图形表征策略解决问题的重要意义。本文借助《求比一个数多几的数》的教学实践与反思,阐述如何在教学中引导学生用图形表征题意,理解数量关系,得出一般的解题策略,建构问题模型,从而提高学生解决问题的能力。
【关键词】图形表征;建构模型;低段数学
《求比一个数多几的数》是人教版二年级上册第二单元《100以内的加法和减法二》的例3,本课内容是在一年级下册“求比一个数多几或少几”的基础上进行学习的。“求相差”、“求比一个数多几”和“求比一个数少几”其实是同一类问题之间的相互转换,但也是低段孩子学习的一个难点,需要借助有效的数学策略使孩子学会分析数量关系。教材用画图的方法分析问题,以理解题意,找到解决问题的方法。在教学中,笔者立足学生已有的知识经验,找寻合适的衔接点,引导学生运用图形表征理解数量关系,从而让学生在已有基础上不断提升认识,构成完整的认知体系。
一、对比铺垫,突破“同样多”
本节课要求学生理解和掌握“求比一个数多几的数”实际问题的数量关系,就必须先理清较大数是由“和较小数同样多的部分加上多出来的部分”组成的。所以本节课复习环节通过对比,突破“同样多”,为新知作好铺垫。
教学片断如下:看图说说
(1)○○○○
△△△△△△
△比○多( )。
师:你是怎么看出来的?
生1:○有4个,△有6个,6-4=2,所以△比○多2个。
生2:一个△与一个○对应起来,△多出来2个。
师:还可以说○比△少( )个。
(2)○○○○○
△△△
△比○少( )个。
师:你是怎么看出来的?
(3)○○○
△△
△比○多2个,△有几个?
师:你是怎么想的?多了2个是哪2个?请你找出○和△同样多的部分,再找出△比○多的部分,△可以分成哪两部分?
生:△可以分成与○同样多的部分和比○多的部分。
课件出示对比图都会用虚线上下一一对应,并把较多的图形分成两部分:同样多的部分和多(少)出来的部分。根据学生已有经验,图形对比,明示数量关系,直观地比一比“谁比谁多几、谁比谁少几”,进一步理解“同样多”,为新授课作好铺垫。
二、图形表征,理解数量关系
图形表征是低段孩子学习数学的一种有效的策略,帮助孩子学会分析数量关系。图形表征在数学解决问题中起着相当重要的作用,图形表征可以使抽象的题变得形象,运用图形表征可轻巧地找出一些文字中未经解释的有用信息,促进问题的解决。低段孩子图式意识薄弱,在具体的教学活动中教师应通过有效指导,展现图形表征过程,体现由具体到抽象的理解过程。
教学片断如下:出示主题图
1. 读题,尝试画图
师:轻声读题,找出数学信息与问题。你能解决它们吗?你能用一幅简单的图来表示题目的意思,再列算式解决这道题吗?
学生试做,师巡查(找有用的信息:实物小红旗,圆形或三角形图)
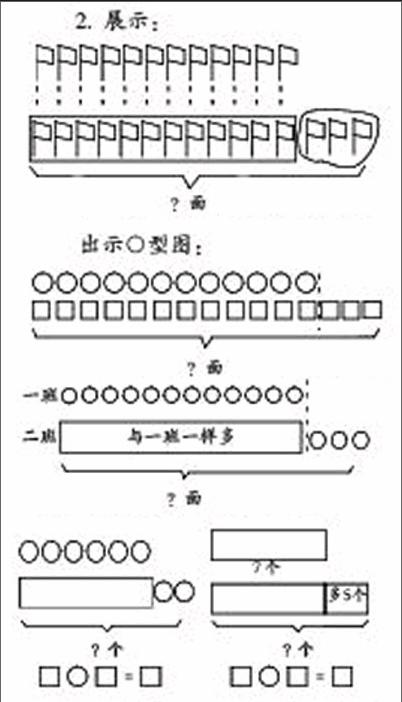
2. 展示:
师:你们能看懂这幅图的意思吗?请画这幅画的小朋友来说说你是怎么画的?
生:先画一班12面小红旗,再画二班比一班多3面小红旗。
师:多3面小红旗在哪里?那前面部分表示什么意思?
生指出多出部分,并回答:前面表示与一班同样多的部分。(用红笔圈起来,并写上“与一班同样多”)
师:谁听明白了他是怎么画出二班的小红旗呢?
师小结:先画与一班同样多的部分,再画多出来的部分。
师:他的信息表达清楚了,问题表达清楚了吗?(补充完整。)
出示○型图:
师:你们看懂这幅图了吗?信息问题有没有表示清楚?请大家观察比较这两幅图,有什么不同?
师:是的,我们可以用简单的图形表示题目的意思。
(师板贴“一班”:12个○,直接出示“二班”、“与一班同样多”,再贴出3个圆。)
师:要解决的问题是什么?(用大括号把两部分括起来“?面”)现在求二班有多少面红旗,算式“12+3=15”对吗?12表示什么?3表示什么?为什么用加法?
生:12表示与一班同样多的部分,3表示多出来的3面,求二班有多少面红旗就是要把与一班同样多的和多出来的3面合起来。
检验:我们做得对吗?那我们看看:二班比一班多得3面,15面比12面多几?
生:對的,多3。
师:最后我们一起口答:二班得了15面小红旗。
低段学生在学习图形表征的过程,一般都是根据题意,让学生用直观的圆形图来表示,然后进一步过渡到用长方形的长短来表示具体数量的多少。在本节课中,笔者从学生已有知识经验和活动经验出发,引导学生用个性化的图式进行图形表征。在学生独立操作的基础上,教师先对学生作品按层次呈现——红旗图、圆圈,再在黑板上展示长条图,让学生感受到长条图的便捷,建立以“1个条形图代替12面小红旗”的表象,经历由具体到抽象的过程。相信经过教师这样的引领,学生对条形图的理解一定会更深刻,对“求比一个数多几的数”这一问题的数量关系分析得更为透彻。
三、多样练习,建构问题模型
设计合理多样的练习题,由浅入深、由易到难,利用现实的、有意义的问题情境设计练习,不仅能激发学生的学习兴趣,而且有利于学生建构问题模型。
教学片断如下:出示看图列式
师:仔细观察图,选一幅图说一说题目的意思?(生独立说)第一幅图哪个小朋友来讲一讲?
生:第一排有7个○,第二排比第一排多2个,求第二排有多少○?
师:怎么解决这个问题呢?
生:求第二排有多少个○就是把与第一排同样多的部分和多出来的2个○合起来。
师:第二幅图哪个小朋友来讲一讲?
生:第一排有7个,第二排比第一排多5个,求第二排有多少个?
师:谁来指一指哪部分是多出来的5个?(学生指)
师:(指同样多的部分)这部分又是什么意思?
生:与第一排同样多的7个。
在巩固练习环节中,除了简单的模仿练习,设计这样的看图列式目的是让学生进一步提升看图能力,也为理解数量关系和建构问题模型助力。在解决问题中,运用图形表征更能让教师了解学情,读懂学生,更能调动学生思维的积极性,提高学生分析问题和解决问题的能力。
图形表征是问题解决中常用的一种思考策略,也是理解题意、描述问题的方式,而培养学生的这一能力是一个循序渐进的过程。所以,在低段教学中,教师要根据学生的年龄特点,有意识地引导学生利用图形表征解决数学问题,从而不断提高学生的数学能力。
