因材施教落实学法 备考研教强化专项
2017-04-05李祖兴
李祖兴
这次去田阳高级中学(以下简称田高)与该校黄美仙老师同课异构,是承载了精准帮扶、探索课改背景下备考复习课教学改革的使命的,但是,到达田高之前,田高学生的基础怎样,课堂难度如何把握,笔者心里确实没底.为了能上出各自的风格,我们双方在课前也不宜就课程作过多沟通,课前沟通仅限于确定上什么内容和使用什么教辅资料.
一、同课异构备考复习课教学设计思路及教学过程
我们上的是文科班的数学复习课.相对来说,文科生长于形象思维,短于逻辑思维,而数学又是一个逻辑性极强的学科.怎样讲授才易于让文科生接受和掌握,怎样发挥文科生的长处,这是本节课要着重解决的两个问题.
按照该校的教学进度,正好上到立体几何《空间垂直的判定和性质》.几何图像有很好的直观性,便于发挥文科生长于形象思维的特点.为了体现普遍性,在授课过程中,笔者全部使用课本中的例题,不再另外添加和更换.
高考备考复习课教学的基本套路:复习相关知识及相关方法→讲解例题→总结方法和规律→课堂课后训练.以上几个教学环节,一环扣一环,从讲到练,哪一个环节都不能马虎.针对本课的教学内容,笔者决定重点处理好下面几个学习方法.
(一)引导学生运用模型记忆相关定理,指点学生运用解题模式时关注关键细节
垂直关系属于空间中位置关系的特殊情况,在生活实际和工程技术中广泛存在并有着广泛的应用.在立体几何中,很多几何体的体积、面积、角度、距离等的计算都要用到垂直关系,因而,垂直关系是立体几何中最重要的关系之一.
空间中的垂直关系涉及线线垂直、线面垂直和面面垂直三种关系.通常情况下,在立体空间,要判定线线垂直,有时要先判定线面垂直;要判定线面垂直,则要先判定另外的线线垂直;要判定面面垂直,则要先判定线面垂直.三种垂直关系的判定方法较多,且都有一定难度,就算是理科生也不易掌握.以往各种资料和很多一线教师都习惯于编成顺口溜让学生记忆,如:线线垂直则线面垂直,线面垂直则线线垂直;线面垂直则面面垂直,面面垂直则线面垂直;等等.但是,实践证明,学生虽然能背得顺口,却不能把握知识的要领.究其原因,实际应用有难度是一个方面,缺少必要的图像直观也在一定程度上阻碍了文科生的准确认知.为了突破这个教学难点,我根据图像直观性强及文科生长于形象思维的特点,选择了用图像记忆定理的教学方法.
关于线面垂直的判定定理:如果一条直线垂直于一个平面内的两条相交直线,那么这条直线就垂直于这个平面.用图像表示,如图1.
在图1中,平面α内的两条相交直线突出地表示了“一条直线垂直于一个平面内的两条相交直线”的特点.学生一经理解,无须文字,对图像所包含的意思也会一目了然,因而极易掌握.
关于线面垂直的性质定理:如果一條直线垂直于一个平面,那么,这条直线就垂直于这个平面内的任何一条直线.用图像表示,如图2.
在图2中,平面α内只有一条直线,明显地表示了“线面垂直则线线垂直”这个要点.学生一经理解,见图就能生义,知道图像的内涵.
关于面面垂直的判定定理:如果一条直线垂直于一个平面,那么,经过这条直线的任何一个平面都垂直于这个平面.用图像表示,如图3.
关于面面垂直的性质定理:如果两个平面垂直,那么,在其中一个平面内且垂直于两个平面的交线的直线垂直于这个平面.用图像表示,如图4.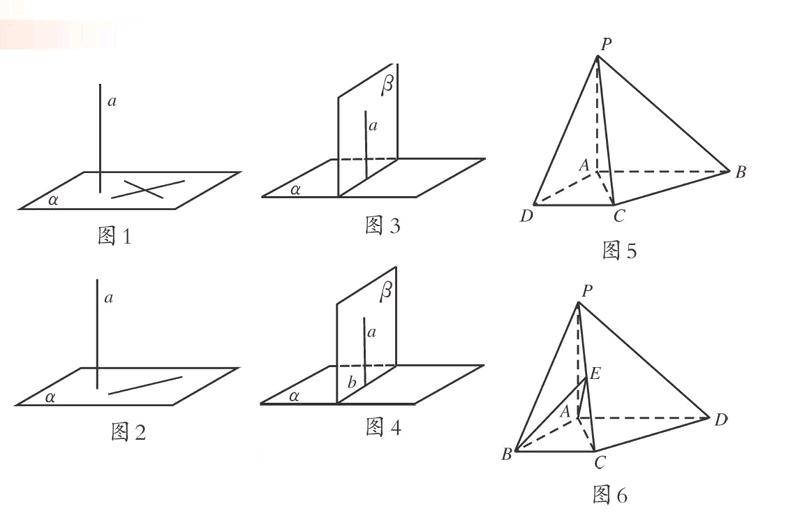
图像识记,无须繁复的文字表述,直观简明,便于理解,也便于识记,而且还为各种变形的形式提供了最直观简明的基本模型.
其实,关于线线垂直、线面垂直、面面垂直的判定方法远不止上面列举的这些,这些垂直的判定和性质以及各种判定方法等合在一起,还是一个不小的系统,以学生现有的基础来说,如果仅用顺口溜文字记忆,反而容易导致知识点之间的相互干扰,配上图形以后,结果就大不一样了,从上面几例就可以感受到这一点.
当然,如果仅仅这样罗列定理,尽管配合了直观的模型,其实还是一种无序的堆砌,要使学生更好地掌握和应用相关的知识,必须有一个总纲,这是不可或缺的两个细节:第一,在空间,线面垂直、面面垂直最终都要归结到线线垂直的判定,因而,线线垂直的判定是关键;第二,空间中也有平面图形,因此,对于同在一个平面内的两条直线的垂直的判定,平面中的判定方法可以照搬过来,如等腰三角形底边上的中线垂直于底边、直角三角形两直角边互相垂直等,都是浅显而又常用的结论.第一点主要为各种垂直的判定指明方向,给出解决问题的思路,有效降低难度,即无论是哪一种垂直的判定,最终都要归结到线线垂直的判定上;第二点主要用于解决思维的惯性问题,让学生明确,在空间中也有平面情形,不可对空间中的平面图形视而不见.有了这两点,学生做起题来就会有章可循,目标明确,从而减少盲目性.
(二)执果索因和化难为易是解决复杂问题的重要思想方法
俗话说,万事开头难.这个开头包括中间过程每一个问题的切入点,而开头难多数情况下是方向不明所致.方向不明,便无从入手.因此,引导学生弄清思考的方向、寻找解决问题的切入点是解题的关键.笔者决定用下面例题的解决过程,引导学生掌握执果索因的解题方法.
例1 如图5,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠ABC=45°,DC=1,AB=2,PA⊥底面ABCD.
(1)求证:AB∥平面PCD;
(2)求证:BC⊥平面PAC.
以下是教学片段实录.
师:本节主要是解决垂直的判定问题,且第一问不算难,同学们课后自行解决就可以了,在此,我们重点解决第二个问题.请问,要证明直线BC⊥平面PAC,只要证明什么就可以了?
生:只要证明BC垂直于平面PAC内的两条相交直线就可以了.
师:哪两条相交直线?
生:PA和AC.
师:(板书“①BC⊥PA;②BC⊥AC”)你们动笔,逐条来证明一下.(一生上讲台在黑板上证明,过程略;师解释黑板上的做法和要点后开始提问)黑板上的做法中,证明①用了什么方法?
生:用了线面垂直的性质定理.
师:证明②用了什么方法?
生:用了勾股定理(注:用勾股定理中计算的方法证明垂直关系).
这个教学过程旨在把学生的思维逐步引导到要解决的基本问题上,方向直指①和②.实际的进程是,这个方向一旦明确了,余下的证明过程学生就能自行完成了.
当然,本例难度不大,但学生在解题前后的表现说明,学生能顺利地自行完成,前面方法与细节的梳理很重要,而解题过程中方向的引导起到了至关重要的作用,这个方向引导,便是执果索因的方法引导.执果索因的主要套路:要解决问题A,需先解决问题B;而要解决问题B,又需要先解决问题C;等等.这就好比顺藤摸瓜,抓住了藤,就能顺着藤一步一步地摸下去,例1便是顺着执果索因的“藤”摸到了解决问题①和②的“瓜”.
执果索因的方法不仅容易把握问题方向,而且另有一个重要作用.我们再看一个例题.
例2 如图6,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
例2中,对于(1)的解题思路引导与例1相仿,在此不再重复.针对(2),要证明PD⊥平面ABE,须先证明PD垂直于平面ABE内的两条相交直线,从最简的角度审视,这两条直线应是AB和AE;而要证明PD⊥AE,必须先证明AE⊥平面PCD,从而必须先证明AE垂直于平面PCD内的两条相交直线,等等.显然,这里出现了较多的转换过程,解题的难度加大了,学生明显露出了困惑的神情.怎样引导学生克服这个难点呢?以下是片段实录.
师:要证PD⊥平面ABE,应先证明什么?
生:先证明PD垂直于平面ABE内的两条相交直线(判定定理).
师:哪两条?(生思考良久后试探性地说出AB和AE;师板书“①PD⊥AB,②PD⊥AE”)怎样证明①呢?
生:(思考良久)先证明AB⊥平面PAD.(师板书“③AB⊥平面PAD”)
师:怎样证明②呢?
生:(思考良久,有学生轻声说出)先证明AE⊥平面PCD.(师板书“④AE⊥平面PCD”)
师:好!只要证明了③和④,就可以解决本题了.现在你们可以仿照例1的方法来完成③和④的证明了.
本例有較大难度,且学生是文科生,有了上面的引导,虽然费了一些周折,但大多数学生最终还是顺利完成了证明过程.该解题过程不仅用到了执果索因的方法,而且突出了另一种重要的数学思想,即化难为易的思想.化难为易,就是通过一定的变换,把原来较难解决的问题转化为另外一个或多个比较容易解决的问题,然后再求解.化难为易的思想方法是解决复杂问题时常用的一种思想方法.
题目之所以难,往往是因为综合了两个或两个以上的知识点,或是条件和结论之间须经多次转换后才能连通起来.但是,不管是哪种情况,中间过程要解决的问题都不止一个,有时甚至是多个.问题越多,或是过程转换越多,条件与结论之间的联系就越不明显,学生就越难把握其中的逻辑关系.例2(2)中的条件和结论的关系就很不明显,要解决的问题也不只一个,但是,先把原问题“化难为易”分解出问题①和②,进而分解出问题③和④,然后逐一解决这些简单的问题,便可最终破解以上困局.这里的分解过程,就是把要解决的复杂问题分解为简单问题的过程.当一个又一个简单问题从复杂的问题中拆解出来之后,问题背后的逻辑关系也就慢慢显现了出来,整个解题思路也就贯通了.
高三学生基本都有了一定的知识和方法储备,缺少的往往是把握这些知识和方法背后严密逻辑的能力.上面两例对于执果索因和化难为易思想方法的运用,无疑为该校师生提供了一个范例.但是,笔者在课后一直纠结,从一直执教理科班数学课程,到这次冷不丁上了一堂文科班的复习课,而且是上优秀生源流失不少后的文科班的课,尽管笔者对本课内容的难易程度、讲解详略、节奏快慢等都尽量做出了调整,但与实际还是有所偏离,比如在讲解例2(2)时,学生的回答出现了明显的迟疑,目光变得迷惘.显然,设置这样难度的问题对学生来说有较大困难,这是笔者预先没有想到的.这是垂直关系的第一课时,像例2(2)这样的难度放在第一课时确实是难了点儿.由此笔者突然顿悟:要使课堂高效,教学内容的难度一定要切合学生的实际;而要做到这一点,教师必须在了解学生的基础上,尽可能地站在学生的角度去思考.教师只有从学生理解和思考问题的角度去分析和预设问题,才能从学生的角度感受到问题的“真实难度”,才能真正知道学生迷茫的根源,也才能够在真正的关节点上为学生指点迷津、指引方向.我想,学生听很多老师讲课时感到稀里糊涂、不得要领,大概就是这个教师“不解学情”的原因在作怪.课后有一位当地的老师夸我讲得真细,这正反映了这种状态:我们的教师常常觉得问题简单,以为学生已经掌握,因而复习时不仅不细,甚至只是形式上略略地提一下,这对学生的复习来说是毫无益处的.比如笔者对已学定理的梳理和点拨,如果不那么详细,如果不配以直观图形帮助学生理解,学生对例1的解答就未必有那么顺畅.
二、数学学科系统备考建议
因为对多数薄弱学校的实际情况并不了解,关于学科备考,笔者只能凭感受和经验,简单谈谈自己的几点见解,供大家参考.
(一)以研促教,提高课堂效率
教师帮助学生复习的主阵地在课堂,课堂教学是影响复习效果至关重要的一个环节.笔者感到,如何不断提高薄弱学校教师的业务水平来保证课堂教学质量,确实是一个非常突出的问题.
笔者这里所说的研究,并不是通常大家理解的要达到一定的知识和能力水平才能进行的研究,而是希望教师们能够留心琢磨教学中遇到的每一个细节,如内容怎样选择、讲解怎样精练、节奏是否符合学生实际、难度如何把握、课后练习如何配备才更有效等,这些是我们每天每节课上都会遇到的问题.教师琢磨问题多了,就会逐渐找出更多更好的方法,不断提高课堂教学效率.当然,在很多情况下,这样的研究是不自觉的,甚至是无意识的.此外,学校也可以多组织一些研究课,多开展一些教研活动,引导教师相互取长补短,学习借鉴他人的经验。长此以往,便会在校内形成一种教研风气,这种风气反过来会促进教师的深度思考和教学水平的不断提高,进而形成教学与教研的良性循环.
(二)编写适合本校的资料
讲授内容、练习资料和测试题目等,过于简单达不到提高的目的,难度过大则无疑废料废题,无论哪一种情况,对学生来说都是无益的,最可怕的是白白浪费了学生宝贵的时间.有句老话说得好,适合的才是最好的.学生的情况,本校的老师最清楚,因此,所用资料只有本校老师编写的才应该是最适合的.如果过多地依赖外来的资料,就容易造成學生长期得不到恰当的训练,复习效果就会在无形中大打折扣.当然,这不是说所有资料都须教师亲自编写.但是,本校教师编写资料确实极其必要,特别是训练题和测试题.
(三)强化专项训练
数学高考题的题型有三种,选择题、填空题和解答题.由于选择题和填空题只要结果,不需要写出过程,因而,也就有了一些异于解答题解题过程的方法,甚至有时可以用极其特殊的解法,即“小题不要大做”.这里所说的“小题”,就是指选择题和填空题,“大做”基本上就是指与解答题一样的做法.
有些小题没有特殊解法,只能大做,但每题都大做肯定会出现一连串的问题,一是花费较多的时间,二是因花费了时间而引起心理的焦虑,三是因心理焦虑而影响到解题思路,所谓越急越乱就是如此.
在很多情况下,由于小题的难度确实不是很大,教师很多时候都是由着学生自行完成,或者进行的针对性训练不多,这都会造成学生小题小做的意识不浓、小题小做的方法不多等.要改变这种情况,教师在引导复习的过程中应小题“大做”,带领学生大张旗鼓地做起“小题小做”的训练来.
相应地,解答题也应有专项的强化训练,时间和方式则须根据本校情况而定,在此不再赘述.
(责编 白聪敏)
