机身加筋壁板环向裂纹损伤容限试验与分析

陈安，廖江海，闫文伟，张海英，臧伟锋

(中国飞机强度研究所 三室，西安 710065)

机身加筋壁板环向裂纹损伤容限试验与分析

陈安，廖江海，闫文伟，张海英，臧伟锋

(中国飞机强度研究所 三室，西安 710065)

机身壁板是飞机结构中的主要承力构件，也是损伤的主要产生部位，研究机身加筋壁板的裂纹扩展规律和剩余强度特性具有重要意义。在轴向拉伸载荷作用下，对含环向裂纹的机身加筋壁板进行损伤容限试验；利用ANSYS有限元软件对试验件进行应力强度因子分析，估算裂纹扩展寿命；基于线弹性断裂力学准则和线弹性断裂力学加塑性修正准则，计算剩余强度特征曲线，并对比分析计算结果和试验结果。结果表明：计算得到的裂纹扩展寿命与试验结果的相对误差为6.3%，满足工程要求；线弹性断裂力学加塑性修正准则估算的剩余强度更为合理，误差仅为2.6%，且偏安全。

机身加筋壁板；环向裂纹；损伤容限试验；应力强度因子

0 引 言

20世纪70年代中期，损伤容限设计技术以飞机设计规范的形式被确定为一种新的飞机设计和评定方法[1]，该技术是在断裂力学理论建立并发展完善的基础上，结合以往的飞机设计经验而提出的。随着对飞机整体性能要求的不断提高，基于损伤容限设计思想的结构设计方法已被广泛应用于飞机结构设计中。目前，国内外对于结构的损伤容限设计也进行了一些研究[2-3]。

机身壁板是飞机结构中的主要承力构件，其几何形状及受载情况较复杂，是损伤的主要产生部位。为了保证飞机结构的设计寿命，需要对机身壁板等重要结构和部位进行损伤容限试验和分析。P.M.G.P.Moreira等[4]对含中心裂纹的整体壁板进行了三维有限元分析，讨论了筋条的几何尺寸对应力强度因子的影响；G.I.Nesterenko等[5]对俄罗斯民用飞机典型壁板进行了损伤容限分析和抗疲劳优化设计，介绍了结构材料的抗裂性研究进展；陈安等[6]对复杂载荷下含纵向裂纹机身加筋壁板进行了损伤容限试验研究，获得了机身壁板的裂纹扩展规律和剩余强度特性；李亚智等[7]以整体加筋壁板和相同构形的铆接加筋壁板为研究对象，对其进行了应力强度因子和剩余强度的计算对比研究；肖群力等[8]对典型机翼整体壁板进行了止裂特性分析和优化设计。上述研究大多偏重数值模拟计算，而对于机身壁板的损伤容限试验研究甚少，缺乏试验结果对理论分析的数据支持。

本文着重进行机身加筋壁板损伤容限试验与理论研究的对比分析。首先，在轴向载荷作用下，对含环向裂纹的机身加筋曲板结构进行裂纹扩展和剩余强度试验；然后，利用有限元软件计算不同裂纹长度下的应力强度因子，分析预测机身壁板的裂纹扩展寿命，并给出剩余强度特征曲线，以期为机身损伤容限设计及评定提供依据。

1 试验方法及装置

1.1 试验件

机身壁板环向裂纹试验件的几何尺寸为2 840 mm×2 054 mm，蒙皮半径为1 671 mm，如图1所示。

试验件由7根长桁、5个框和蒙皮组成，长桁间距192 mm，框间距483 mm。蒙皮采用2524-T3铝合金板件铣切而成，该材料的力学性能如表1所示；长桁和框的材料均为7075-T62铝合金。

表1 2524-T3铝合金力学性能

蒙皮厚度为1.20 mm，长桁厚度为1.60 mm，框厚度为1.27 mm。试验件在3#和4#框中间沿环向预制长度2a=25 mm的初始裂纹，裂纹穿过中央4#长桁。

1.2 试验载荷

损伤容限试验分裂纹扩展试验和剩余强度试验两个阶段进行。机身壁板为前机身等直段上壁板，根据飞机1 h典型飞行任务剖面全机有限元分析结果，获取裂纹扩展试验轴向拉伸载荷的最大值为227.1 kN，应力比R=0.1，采用等幅谱施加载荷。剩余强度试验载荷是裂纹扩展试验载荷的1.5倍，即340.7 kN。

1.3 试验支持与加载

根据试验件的受载形式，设计立式自平衡试验加载装置对试验件进行支持与加载，如图2所示。

试验装置主要包括加载框架、作动筒、加载横梁、均载器和拉板杠杆系统。试验件上端曲边通过加载横梁将均载器和作动筒连接，利用作动筒实现主动加载。试验件下端曲边通过拉板杠杆系统连接均载器，均载器固定在试验加载框架的底座上，底座与试验厂房地轨连接。

2 损伤容限试验结果

2.1 裂纹扩展试验

裂纹扩展试验中，采用贴标尺和读数显微镜目测的方法对半裂纹长度a进行测量。裂纹扩展路径如图3所示，可以看出：环向裂纹基本沿直线扩展。

每循环一定次数，记录a和循环次数N，试验的a-N曲线如图4所示。

从图4可以看出：左右两侧裂纹扩展对称性较好，左侧裂纹扩展速率略低于右侧裂纹，总体扩展趋势一致；裂纹从半长12.5 mm扩展到70 mm，载荷循环了22 318次，在此过程中裂纹扩展比较缓慢；裂纹扩展到半长70 mm以后，呈快速扩展趋势，从70 mm扩展到180 mm，载荷循环了3 195次，裂纹扩展速率明显加快；在接近两跨长桁时裂纹扩展速率有所减慢，表明长桁对裂纹有止裂作用；当裂纹扩展至两跨长桁时，即两侧半裂纹长度为192 mm时，停止裂纹扩展试验，此时裂纹扩展寿命为26 040次。

2.2 剩余强度试验

在裂纹总长度为384 mm时停止裂纹扩展试验，并开始进行剩余强度试验。加载至153%剩余强度试验载荷时试验件破坏，即轴向拉伸载荷为521.3 kN。剩余强度试验破坏结果如图5所示。

从图5可以看出：试验件沿环向裂纹方向完全断裂破坏。经检查，机身壁板试验件7根长桁全部断裂破坏，同时部分铆钉断裂。

3 数值计算分析

3.1 有限元应力分析

利用ANSYS软件建立有限元模型并进行应力强度因子分析。建模过程忽略部分圆角和倒角，蒙皮、长桁、框均采用8节点SHELL93壳单元模拟，铆钉采用2节点BEAM188梁单元模拟，裂纹尖端采用由8节点等参元蜕化构造的奇异元模拟。根据试验结果裂纹模拟沿直线扩展，含环向裂纹壁板的有限元模型如图6所示。

机身壁板模型的边界条件按照试验情况施加，即下端曲边蒙皮节点：位移Uz=0，转角ΦR=Φz=0；上端曲边蒙皮节点：转角ΦR=Φz=0，并在该边界的蒙皮节点上施加均布轴向拉伸载荷，所加载荷为裂纹扩展试验载荷。

3.2 应力强度因子计算

蒙皮环向裂纹尖端应力强度因子变化曲线如图7所示。

从图7可以看出：在半裂纹长度小于160 mm时，左右两侧裂纹尖端应力强度因子都线性增大，左侧裂纹应力强度因子略低于右侧裂纹；当半裂纹长度超过160 mm时，左右两侧裂纹尖端应力强度因子有所降低，且随着裂纹长度的增加，两侧裂纹尖端的应力强度逐渐降低，直至裂纹扩展至两跨长桁。

应力强度因子的变化规律表明：当裂纹长度较短时，裂纹尖端距离长桁较远，应力强度因子呈线性增加趋势；当裂纹扩展到长桁附近时，裂纹尖端的张开位移受到长桁的限制，载荷进行有效地再分配，从而降低了应力强度因子，长桁起到止裂的作用。

为了获得无量纲应力强度因子系数，取轴向名义应力σref，则无量纲应力强度因子系数为

(1)

无量纲应力强度因子系数变化曲线如图8所示，可以看出：β随半裂纹长度的增加而先减小后增加，在靠近两跨长桁时显著减小。

3.3 裂纹扩展寿命分析

对于常幅载荷谱，常用的裂纹扩展计算模型包括Paris公式[9]和Walker公式。由于缺乏2524-T3铝合金Walker公式的相关参数，本文裂纹扩展分析选用工程常用的Paris公式：

(2)

对于2524-T3铝合金，在应力比为0.1的情况下，根据美国铝业公司(ALCOA)提供的数据，式(2)中C=8.27×10-11mm·(N/mm3/2)-n，n=2.653 9。

利用Paris公式计算裂纹扩展寿命，试验裂纹寿命与预测结果对比的a-N曲线如图9所示。

从图9可以看出：在缓慢裂纹扩展阶段，预测曲线与试验实测曲线吻合较好；在裂纹快速扩展阶段，预测结果与试验结果略有差异，原因是Paris公式主要预测裂纹稳定扩展阶段的寿命；预测结果与试验结果的a-N曲线总体趋势一致性较好，预测裂纹扩展寿命为24 398，偏安全，两者的相对误差为6.3%，满足工程要求。

3.4 剩余强度分析

根据应力强度因子曲线，可以计算得到结构的剩余强度特征曲线。作为对比，分别给出基于线弹性断裂力学准则(方法1)和线弹性断裂力学加塑性修正准则(方法2)的剩余强度特征曲线。

按照线弹性断裂力学准则，剩余强度许用值为

(3)

按照线弹性断裂力学加塑性修正准则，剩余强度许用值[10]为

(4)

其中，

[σ]n=σysAn/Ag

(5)

(6)

(7)

式中：μ=0.63；βc=1；βJ为图8给出的无量纲应力强度因子；ay为过渡裂纹长度；σys为材料屈服应力；Kc为材料的平面应力断裂韧性；An为裂纹所在截面的净面积；Ag为裂纹所在截面的毛面积。

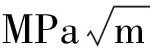
按照上述剩余强度计算方法获得的剩余强度特征曲线如图10所示。

从图10可以看出：随着裂纹长度增加剩余强度降低，当裂纹扩展至长桁附近时，剩余强度略有小幅度增加；在整个裂纹扩展过程中，方法1的值都大于方法2的值，当裂纹小于40 mm时，方法1的剩余强度超过了材料的屈服应力，甚至大于强度极限，这是因为线弹性断裂力学(方法1)未考虑材料屈服的影响；当裂纹较短时(小于100 mm)，方法1计算的剩余强度和方法2计算的剩余强度偏差较大，当裂纹较长时(大于100 mm)，方法1计算的剩余强度和方法2计算的剩余强度偏差较小。

利用剩余强度特征曲线获得半裂纹长度a=192 mm时，两种方法计算的剩余强度载荷对比如表2所示。

表2 两种方法剩余强度对比

从表2可以看出：按照线弹性断裂力学准则(方法1)计算的剩余强度载荷为547.1 kN，大于试验剩余强度载荷4.9%，偏危险；按照线弹性断裂力学加塑性修正准则(方法2)计算的剩余强度载荷为507.6 kN，小于试验剩余强度载荷2.6%，偏安全。因此，采用线弹性断裂力学加塑性修正准则的计算结果与试验结果吻合得更好，预测含环向裂纹机身壁板的剩余强度更合理。

4 结 论

(1) 裂纹扩展试验中环向裂纹基本沿直线扩展，左右两侧裂纹扩展对称性较好，总体扩展趋势一致，半裂纹长度小于70 mm时呈缓慢裂纹扩展特性；环向裂纹扩展到两跨长桁时，剩余强度载荷可达设计载荷的153%。

(2) 利用Paris公式计算得到的裂纹扩展寿命与试验结果的a-N曲线趋势一致性较好，计算结果偏安全，相对误差为6.3%，满足工程要求。

(3) 对于含环向裂纹的机身壁板，由于两跨裂纹尺寸相对较短，建议采用线弹性断裂力学加塑性修正准则估算结构的剩余强度。该方法估算得到的含环向裂纹机身壁板的剩余强度与试验结果的误差仅为2.6%，且偏安全。

[1] 王远达, 梁永胜, 王宏伟. 飞机结构的耐久性与损伤容限设计[J]. 飞机设计, 2009, 29(1): 37-43. Wang Yuanda, Liang Yongsheng, Wang Hongwei. Design of durability and damage tolerance for aircraft structure[J]. Aircraft Design, 2009, 29(1): 37-43.(in Chinese)

[2] Shahani A R, Mohammadi S. Damage tolerance approach for analyzing a helicopter main rotor blade[J]. Engineering Failure Analysis, 2015, 57: 56-71.

[3] 蔡玲, 黄其青, 殷之平, 等. 基于损伤容限设计思想的飞机整体翼梁优化设计[J]. 机械强度, 2009, 31(4): 620-624. Cai Ling, Huang Qiqing, Yin Zhiping, et al. Optimum design based on damage tolerance for integrated wing-beam structure[J]. Journal of Mechanical Strength, 2009, 31(4): 620-624.(in Chinese)

[4] Moreira P M G P, Pastrama S D, Castro P. Three-dimensional stress intensity factor calibration for a stiffened cracked plate[J]. Engineering Fracture Mechanics, 2009, 76(14): 2298-2308.

[5] Nesterenko G I, Nesterenko B G. Ensuring structural damage tolerance of Russian aircraft[J]. International Journal of Fatigue, 2009, 31(6): 1054-1061.

[6] 陈安, 魏玉龙, 廖江海, 等. 机身加筋壁板复合加载损伤容限性能试验[J]. 航空学报， 2017, 38(1): 420093-1-420093-8. Chen An, Wei Yulong, Liao Jianghai, et al. Damage tolerance test of stiffened fuselage panel under complex load[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 420093-1-420093-8.(in Chinese)

[7] 李亚智, 张向. 整体加筋壁板的破损安全特性与断裂控制分析[J]. 航空学报, 2006, 27(5): 842-846. Li Yazhi, Zhang Xiang. An analysis of fail-safety and fracture control of integrally stiffened panels[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(5): 842-846.(in Chinese)

[8] 肖群力, 黄其青, 殷之平. 典型机翼整体壁板止裂特性分析及优化设计[J]. 机械强度, 2012, 34(1): 96-100. Xiao Qunli, Huang Qiqing, Yin Zhiping. Analysis of crack-arrest property and optimum design for typical integrally stiffened panel[J]. Journal of Mechanical Strength, 2012, 34(1): 96-100.(in Chinese)

[9] Paris P, Erdogan F. A critical analysis of crack growth laws[J]. Journal of Basic Engineering, 1963, 85(3): 528-534.

[10] 郑晓玲. 民机结构耐久性与损伤容限设计手册:下册——疲劳设计与分析[M]. 北京: 航空工业出版社, 2003: 277-278. Zheng Xiaoling. Durability and damage tolerance design handbook on civil aviation aircraft structure:Ⅱ-damage tolerance design[M]. Beijing: Aviation Industry Press, 2003: 277-278.(in Chinese)

[11] 樊振兴, 李亚智, 王亚星, 等. 含裂纹铝合金薄板的断裂韧度与剩余强度研究[J]. 航空工程进展, 2015, 6(1): 52-58. Fan Zhenxing, Li Yazhi, Wang Yaxing, et al. Study on fracture toughness and residual strength of aluminum alloy thin sheet with crack[J]. Advances in Aeronautical Science and Engineering, 2015, 6(1): 52-58.(in Chinese)

(编辑：马文静)

Damage Tolerance Test and Analysis of Stiffened Fuselage Panel with Circumferential Crack

Chen An, Liao Jianghai, Yan Wenwei, Zhang Haiying, Zang Weifeng

(The Third Department, Aircraft Strength Research Institute of China, Xi’an 710065, China)

Fuselage panel is the main load bearing component in aircraft structure，and also the main damage producing part. It is important to investigate the performance of the crack growth and characteristic of the residual strength for fuselage panel. Experimental study on a stiffened fuselage panel with circumferential crack subjected to axial tension load is presented. Stress intensity factors(SIF) of experimental structure are analyzed by using ANSYS software. The crack propagation life is evaluated. The residual strength curves are calculated based on the linear elastic fracture mechanics and linear elastic fracture criterion modified by yield correction, respectively. The research indicates that the calculated results agree well with the crack propagation test data. The relative error is 6.3%, and the calculation accuracy satisfies the requirement of engineering. The estimation results using linear elastic fracture criterion modified by yield correction is more reasonable than using linear elastic fracture mechanics. The relative error is 2.6%.

stiffened fuselage panel; circumferential crack; damage tolerance experiment; SIF

2016-11-23；

2016-11-30

陈安,andychen1986@163.com

1674-8190(2017)01-038-06

V216.1+1

A

10.16615/j.cnki.1674-8190.2017.01.006

陈 安(1986-)，男，硕士，工程师。主要研究方向：结构疲劳、断裂及可靠性分析。

廖江海(1979-)，男，硕士，高级工程师。主要研究方向：结构耐久性/损伤容限设计与试验验证。

闫文伟(1981-)，男，高级工程师。主要研究方向：结构耐久性/损伤容限设计。

张海英(1982-)，男，硕士，高级工程师。主要研究方向：结构疲劳、断裂及可靠性分析。

臧伟锋(1970-)，男，硕士，高级工程师。主要研究方向：结构耐久性/损伤容限设计与试验验证。