一种基于精确刚度分析的刚性连接单元

何鹏秋，孙秦

(西北工业大学 航空学院，西安 710072)

一种基于精确刚度分析的刚性连接单元

何鹏秋，孙秦

(西北工业大学 航空学院，西安 710072)

NASTRAN刚性连接单元RBE3中的权因子需要人为设定，由此导致分配节点载荷具有较强的主观性。针对该问题，基于结构刚度矩阵的缩聚原理提出一种精确的刚性连接单元，该单元可将指定节点上的载荷精确分配至结构的主要承力节点，并能有效克服RBE3单元中权因子不直观且难以确定的缺点。通过算例验证，表明采用本文所提出的精确刚性连接单元可以精确完成由加载节点到主要承力节点的载荷分配计算，且所得载荷分配结果更为精确可靠。

刚性连接单元；RBE3；载荷分配；刚度缩聚；刚度特性

0 引 言

在飞机结构设计中，经常会遇到一些结构参数不确定或者结构强度为非主要研究对象的设计对象。例如，在飞行器机身设计验证阶段，发动机、起落架等不确定或复杂结构可以适当简化为一个节点，只需将这些结构上作用的载荷等效传递至机身便可完成机身结构的初步设计及强度校核。这样既有效提高了整机有限元数值分析的建模效率，又能避免由于模型结构不确定而导致无法进行结构有限元力学性能分析的问题。

在载荷传递分析中，多使用NASTRAN中的刚性连接单元RBE3完成由指定加载节点到主要承力构件的载荷传递分析[1-3]。由于RBE3建模方便，目前已被广泛应用于飞机机翼和机身设计[4-5]、火箭动力特性分析[6-7]、导弹固有特性分析[8]、汽车应力强度分析[9]、卫星固有频率分析[10]等有限元数值仿真中。在RBE3单元中，各个主要承力节点上的分配载荷主要通过用户指定的权因子来分配计算[11-12]，用权因子来表征不同承力节点处的刚度特性。

然而，该方法也有不足之处，首先，它假定主要承力节点中的每一节点在不同方向上的刚度特性相同，但实际上结构在不同方向上的刚度值通常存在较大差异，例如对一个薄板进行弯曲远比对其进行拉伸容易，故假定节点在各个方向上的刚度一致是不合理的；其次，RBE3单元中权因子的取值大小通常难以估计，原因是主要承力构件的刚度特性与结构形状、材料以及边界约束条件等密切相关，通常将权因子设置为1，即默认各个承力节点的刚度特性都相同。综上所述，利用RBE3刚性连接单元得到的分配载荷具有较大的主观性、不合理性。

本文针对RBE3单元的上述缺点，提出一种更为精确的刚性连接单元，该单元可由主要承力结构的真实刚度得到主要承力节点与加载节点间的载荷分配关系，并通过数值算例验证该单元的精确性。

1 传统RBE3单元技术

主要承力节点与加载节点如图1所示，gi(i=1,2,…,n)为承力节点，r为指定的加载节点，也称作相对参考点[9]。

在RBE3单元中，根据力与力矩的平衡关系，先将节点r上的载荷等效传递至权值重心B，即

FB=Fr

(1)

MB=Mr+Fre

(2)

式中：e为B点到r点的向量。

得到B点处的力和力矩之后，则该力和力矩在节点gi处的分配载荷分别为

(3)

(4)

式中：wi为用户指定的权因子；ri为节点gi到B点的距离。

Fi1的方向与Fr平行，Fi2与节点gi到B点之间的向量垂直。由弯矩MB得到的分配载荷如图2所示。

从式(3)～式(4)可以看出：该单元相当于在节点r上先建立一个刚性平板，然后在各个主承力构件节点与刚性平板相交处建立一个刚度为wi的弹性连接，由该弹性连接完成由加载节点到主要承力节点载荷的分配。

假设节点gi和加载节点r的线位移分别为ugi和ur，角位移分别为θgi和θr。通过刚体位移约束关系，gi点的线位移和角位移可由r点的线位移和角位移线性唯一表示：

(5)

定义R=[R1R2R3]为挂载结构节点r到主要承力节点gi的距离向量。将主要承力节点依次代入式(5)，可得

ug=G ur

(6)

式中：G=[G1G2… Gn]T，n为主要承力节点的个数。

在RBE3单元中，主要承力节点与刚性平板间弹性连接的刚度由用户指定的权因子wi确定，即刚度矩阵Kg中节点gi对应的对角线值为wi。因此，弹性连接的载荷位移平衡方程为

Fg=Kgug=KgGur

(7)

与式(6)的形式相似，在刚性连接中，挂载结构节点r与承力节点gi之间的载荷满足[10]：

Fr=GTFg

(8)

将式(7)左乘GT，并将式(8)代入其中可得

ur=(GTKgG)-1Fr

(9)

由式(7)和式(9)可得承力节点处的载荷分布为

Fg=KgG(GTKgG)-1Fr

(10)

式(10)即为RBE3单元载荷传递分配公式的矩阵表达形式。从式(10)可以看出：Kg的取值直接决定着主要承力节点的载荷分配结果，而Kg交由用户来确定，这显然是不合理的。

2 新型刚性连接单元

不同于式(10)中主要承力节点的刚度特性由用户指定的权值来确定，本文提出一种更为精确的刚性连接单元，即通过系统真实结构刚度矩阵的缩聚方法获得承力节点集的刚度特性。令g-集表示有限元结构中的主要承力节点集，l-集表示不包含主要承力节点的节点集，则有限元结构的平衡方程为

(11)

即l-集与g-集的位移约束关系满足：

(12)

代入式(11)即得g-集的位移载荷关系:

(13)

因此，承力节点集的刚度矩阵为

(14)

将缩聚后得到的刚度矩阵代入式(10)中，得到精确的载荷分配关系：

(15)

相比于RBE3刚性连接单元，由刚度矩阵缩聚方法得到的缩聚刚度矩阵能精确描述主要承力节点集的刚度特性，为获得精确的载荷分配关系提供了可靠的数值分析基础。

3 数值算例

3.1 简单薄壁结构验证

简单薄壁结构的有限元模型如图3所示，该结构包含两个三角形板和一个圆柱梁。三角形板的底边边长为1.000m，高为0.400m，厚度为0.002m，采用四边形壳单元对其进行网格划分；圆柱梁的半径为0.005m，长度为0.400m，采用梁单元对其进行网格划分。材料的弹性模量E=2.06×109Pa，μ=0.3。在D点处作用一个竖直向下的单位载荷F=1，该载荷通过RBE3单元传递至A、B、C三个主要承力节点。下文将分别采用RBE3单元和本文提出的刚性连接单元对上述简单薄壁结构进行载荷传递分析。

RBE3单元权因子设置为默认值，即wi=1。A、B、C三个节点处分配载荷的理论解可由刚度分配原则直接得到。具体方法为：在A、B、C三个节点处施加竖直向下的单位位移，由相应的节点力可得三个节点竖直方向的刚度值，分别为2.065 5×106、4.044 8×105、2.065 5×106N/m；再按照刚度分配原则精确得到A、B、C三个节点处分配载荷的理论解。

RBE3单元和本文所提出的刚性连接单元对图3中简单薄壁结构的载荷分配结果对比如表1所示。

表1 主要承力节点载荷分配结果对比

从表1可以看出：采用本文方法所得载荷分配结果与理论解一致，而RBE3单元得到的载荷分配结果则是由加载节点载荷除以3直接得到，完全忽略了结构刚度对载荷分配的影响。此外，由RBE3单元得到的B点载荷约为理论解的4倍，这在工程上是无法接受的，甚至被认为是错误的。这表明本文提出的刚性连接单元是一种有效的、精确的刚性连接单元。

3.2 机翼薄壁结构验证

机翼薄壁结构的有限元模型如图4所示，对其在发动机载荷作用下的受力进行分析。机翼展长为1.196 0m，翼根弦长为0.814 0m，翼尖弦长为0.457 0m，蒙皮厚度为0.002 0m，翼肋厚度为0.001 5m，梁腹板厚度为0.001 5m。在机翼下方采用刚性连接单元连接简化的发动机模型，发动机质量M=1 010kg，结构过载为1，发动机推力为69.4kN。

采用本文方法得到的机翼连接节点的载荷分配情况如表2所示，RBE3单元在不同权值设置下的载荷分配结果如表3～表4所示。

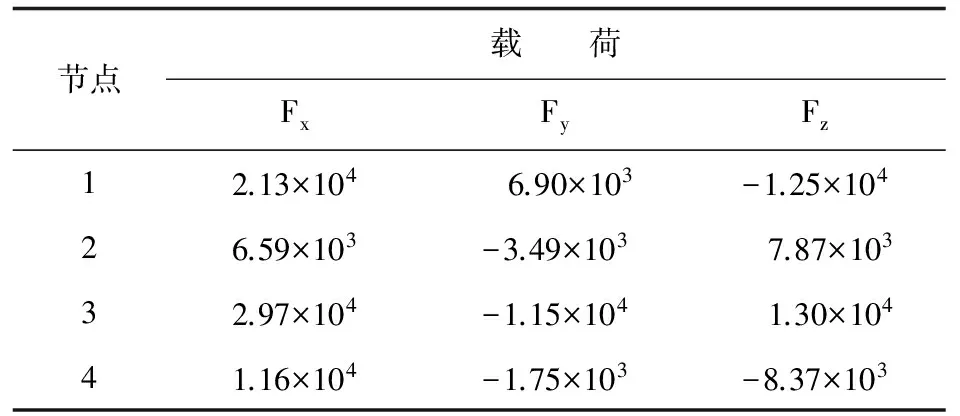
表2 精确刚度分析法机翼节点载荷分配情况

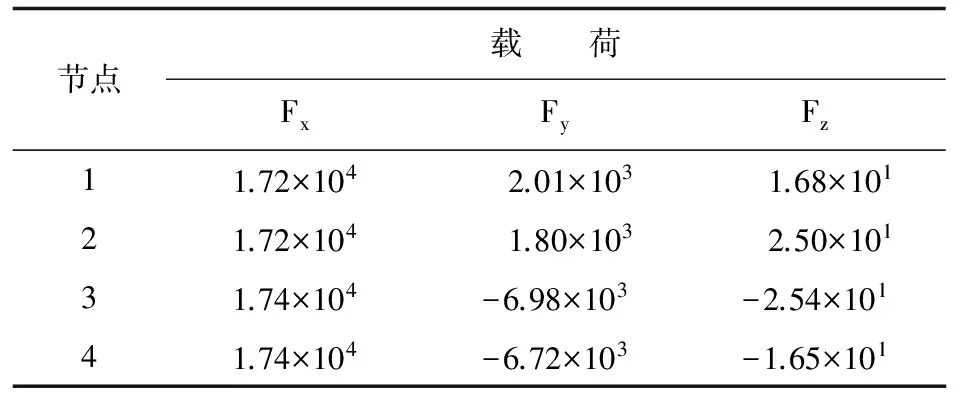
表3 RBE3载荷分配情况(w1=w2=w3=w4=1)

表4 RBE3载荷分配情况(w1=w2=1，w3=w4=2)

从表2～表4可以看出：采用不同的权值对RBE3单元的计算结果有较大影响；RBE3单元的权值设置方法与本文精确的刚度分析方法所得到的节点分配载荷具有明显差异，其原因是不同结构节点在不同方向上的刚度差异较大。这进一步表明本文所提出的方法能够有效克服主观人为因素对分析结果的影响，更具优越性。

4 结 论

(1) 本文通过刚度矩阵的缩聚原理，精确得到主要承力节点集的刚度特性，为进一步精确得到主要承力节点与加载节点间的载荷分配关系提供了基础。

(2) 本文所提出的精确刚性连接单元能够有效克服RBE3单元的两个不合理假设，计算过程简单，分析所得的载荷分配结果更为精确可靠，在工程实际应用中具有重要意义。

[1] 江鹏. 飞机外蒙皮上非受力结构有限元模型设计浅析[J]. 科技创新导报, 2011(12): 45-46.JiangPeng.Finiteelementmodeldesignofunloadedstructureonouterskinofaircraft[J].Science&TechnologyInnovationHerald, 2011(12): 45-46.(inChinese)

[2] 张友坡. 基于有限元法的飞机舱门结构仿真技术[J]. 中国高新技术企业, 2013(5): 21-24.ZhangYoupo.Simulationofaircrafthatchstructurebasedonfiniteelementmethod[J].ChinaHigh-TechEnterprises, 2013(5): 21-24.(inChinese)

[3]LacavaW,XingY,MarksC,etal.Three-dimensionalbearingloadsharebehaviourintheplanetarystageofawindturbinegearbox[J].IetRenewablePowerGeneration, 2013, 7(4): 359-369.

[4]TeixeiraNA,BussamraFLDS.Anewmetamodelforreinforcedpanelsundercompressiveloadsanditsapplicationtothefuselageconception[J].LatinAmericanJournalofSolids&Structures, 2014, 11(2): 223-244.

[5]GramüllerB,StroscherF,SchmidtJ,etal.Designprocessandmanufacturingofanunmannedblendedwing-bodyaircraft[C].Deutschland:DeutscherLuft-undRaumfahrtkongress, 2015.

[6] 王建民, 吴艳红, 张忠, 等. 运载火箭全箭动特性三维建模技术[J]. 中国科学: 技术科学, 2014, 44(1): 50-61.WangJianmin,WuYanhong,ZhangZhong,etal.Three-dimentionalmodelingtechnologyfordynamiccharacteristicsofthelaunchvehicle[J].ScientiaSinica(Technologica), 2014, 44(1): 50-61.(inChinese)

[7] 李道奎, 刘林, 万军. 牵制释放过程中火箭液体推进剂的建模研究[J]. 强度与环境, 2008, 35(6): 14-18.LiDaokui,LiuLin,WanJun.Studyofthemodelofrocket’sliquidpropellantintheprocessofhold-downandrelease[J].Structure&EnvironmentEngineering, 2008, 35(6): 14-18.(inChinese)

[8] 张琪, 刘莉. 导弹固有特性的有限元分析[J]. 弹箭与制导学报, 2008, 28(2): 6-7.ZhangQi,LiuLi.Finiteelementanalysisofmissileinherentproperties[J].JournalofProjectiles,Rockets,MissilesandGuidance, 2008, 28(2): 6-7.(inChinese)

[9] 邵松标, 刚宪约, 柴山, 等. 整体式车桥有限元分析的位移边界模型研究[J]. 重庆交通大学学报: 自然科学版, 2015, 34(3): 152-156.ShaoSongbiao,GangXianyue,ChaiShan,etal.Displacementboundarymodelingmethodforfiniteelementanalysisofrigidvehicleaxle[J].JournalofChongqingJiaotongUniversity:NaturalScience, 2015, 34(3): 152-156.(inChinese)

[10] 武新峰, 雷勇军, 李道奎. 液体推进剂消耗对大型卫星结构动特性的影响分析[J]. 国防科技大学学报, 2012, 34(4): 38-42.WuXinfeng,LeiYongjun,LiDaokui.Dynamicanalysisofalargescalesatellitestructurewiththeliquidpropellantconsuming[J].JournalofNationalUniversityofDefenseTechnology, 2012, 34(4): 38-42.(inChinese)

[11]NastranMSC.Linearstaticanalysisuser’sguide[M].SantaAnaCA:TheMacNeal-SchwendlerCorporation, 2010.

[12] 张永昌.MSC.NASTRAN有限元分析理论基础与应用[M]. 北京: 科学出版社, 2004.ZhangYongchang.TheoreticalfoundationandapplicationoffiniteelementanalysisusingMSC.NASTRAN[M].Beijing:SciencePress, 2004.(inChinese)

(编辑：马文静)

A New Rigid Connection Element Based on the Accurate Stiffness Analysis

He Pengqiu, Sun Qin

(School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The rigid connection element(RBE3) in NASTRAN requires the user to specify the weight factor of each main structure node subjectively. As a result, the user defined load weight factors make the calculation of the distributed loads inaccurate. To deal with this drawback, a new rigid connection element based on the principle of structure stiffness matrix condensation is proposed to accurately calculate the distributed loads acting at the specified node to the main structure nodes. Consequently, the new element effectively overcomes the subjectivity of the RBE3 element. The numerical results show that the new element can accurately derive the load distribution of the main structure nodes and make the solution of distributed loads more accurate and reasonable.

rigid connection element; RBE3; load distribution; stiffness matrix condensation; stiffness property

2016-12-09；

2017-01-03

国家自然科学基金(51375386)

孙秦,sunqin@nwpu.edu.cn

1674-8190(2017)01-068-05

V214.1

A

10.16615/j.cnki.1674-8190.2017.01.010

何鹏秋(1990-)，男，博士研究生。主要研究方向：有限单元设计、惯性释放、矩阵分解。

孙 秦(1956-)，男，博士，教授，博导。主要研究方向：有限元方法、疲劳与断裂、气动弹性。