隐身飞机机身侧棱电磁散射特点分析

张扬，艾俊强，王健，张维仁

(中国航空工业集团公司 第一飞机设计研究院，西安 710089)

隐身飞机机身侧棱电磁散射特点分析

张扬，艾俊强，王健，张维仁

(中国航空工业集团公司 第一飞机设计研究院，西安 710089)

隐身飞机机身侧棱是侧向重要散射源，研究其电磁散射特点具有重要意义。建立机身侧棱分析模型，采用多层快速多极子算法(MLFMM)进行计算，获得雷达散射截面(RCS)沿水平面方位角的分布数据；构建RCS峰值、波峰宽度、旁瓣均值三维度评价方法，基于该方法分析机身侧棱电磁散射的极化特性和频率特性；针对棱边长度、棱边尖劈角、棱边厚度三项关键几何参数，建立变参数模型并通过仿真研究RCS对几何参数的敏感性。结果表明：RCS峰值对棱边长度及棱边尖劈角比较敏感，波峰宽度对频率比较敏感，旁瓣均值对频率及棱边尖劈角比较敏感。

隐身飞机；棱边；电磁散射；RCS

0 引 言

隐身飞机普遍应用了低雷达散射截面(Radar Cross Section，简称RCS)机身剖面设计技术。从目前国内外隐身飞机的外形来看，机身侧面都采用带有棱边的形式，这样可以避免机身的镜面强散射，使之成为较弱的棱边绕射[1-3]。然而，对于进一步追求侧向隐身性能的飞机来说，需要通过隐身优化设计对棱边的散射进行控制。因此，有必要对机身侧棱边的电磁散射特点进行研究。

白振东等[4]对机身剖面参数化进行了研究，建立了机身典型剖面模板参数，但未进一步研究所定义的参数对机身RCS的影响。桑建华[5]对飞机翼面的边缘绕射进行了描述，指出机翼前缘的最大散射出现在入射电场平行于边缘时，并给出了隐身飞机机身侧棱散射特征的预估公式。阮颖铮[6]对尖劈边缘绕射理论进行了深入分析。上述文献着重介绍了棱边散射的求解方法，对其具体的散射特点介绍较少。姬金祖等[7]、张考等[8]和李启鹏等[9]从隐身角度对机身剖面部分几何参数进行了研究，但都存在几何参数不全面、评价标准较单一的问题。

本文建立机身侧棱模型并对其进行仿真，从RCS峰值、波峰宽度、旁瓣均值三方面进行综合分析，研究机身侧棱的极化特性、频率特性，对于棱边长度、尖劈角、厚度等关键几何参数进行变参数研究，并获得其对RCS的影响规律。

1 建 模

分析模型的设计基准是飞机构造水平线和飞机对称面。在考察飞机某个侧向时，该侧棱边为主要散射源，另一侧散射贡献较小，因此本文将单侧棱边取出进行单独研究。将机身剖面沿飞机对称面分割，取其中一半进行拉伸。为了避免除棱边之外的其他边缘对结果造成干扰，将上、下表面边缘光滑过渡，形成低散射载体。此时，过棱边中点的棱边法平面为模型对称面。基本模型棱边长度为5.00 m，厚度为0 m(尖劈状)，上表面切线与水平面夹角为30°，下表面切线与水平面夹角为15°，模型总宽度为3.04 m，最大高度为2.27 m，如图1所示。变参数模型将在基本模型基础上对棱边长度、切线夹角、棱边厚度进行改变。

仿真所用的算法为多层快速多极子方法(Multilevel Fast Multipole Method，简称MLFMM)。该方法采用加法定理进行分层分区，近区耦合基于矩量法直接计算，非附近区耦合由聚合、转移、配置三步完成[10-12]。上述计算方法与微波暗室测试结果吻合较好[13-15]，表明该方法应用于电磁散射特点分析是可行的。

定义电磁波在水平面内垂直棱边照射时方位角为0°，垂直侧端面照射时方位角为90°，垂直于后端面照射时方位角为180°。考虑到模型的对称性，仅计算方位角为0°～180°的RCS。定义电场方向水平时为HH极化，电场方向垂直于水平面时为VV极化。监视警戒雷达为飞机重要威胁之一，一般作用在L波段与S波段，基于此，本文主要研究低频段(频率4.0 GHz以下)的电磁散射特性。真实飞机蒙皮一般为金属，故计算中将模型作为理想电导体处理。采用远场平面波照射，计算类型为单站RCS。

对于计算曲线，分析认为方位角0°～45°之间的数据可表征机身侧棱边的RCS，其余部分为载体的贡献。在该方位角区间，由于棱边散射存在，0°方位角附近出现强RCS波峰，其余部分RCS值相对较低。针对此特点，定义RCS波峰为0°方位角附近RCS大于-10.0 dB的曲线部分，其余部分为散射旁瓣(45°方位角之内)。由于RCS曲线随方位角波动较大，为了定量分析电磁散射特点，在上述波峰和旁瓣定义的基础上，引入RCS峰值、波峰宽度、旁瓣均值三项考察指标。RCS峰值是指0°方位角时的RCS值，即垂直照射棱边时的RCS值；波峰宽度是指波峰所占方位角区域大小，根据对称性考虑±45°方位角内波峰的总宽度；旁瓣均值是指去掉波峰后剩余部分(45°方位角之内)的RCS均值。通过以上三个维度的对比，能使电磁散射特点的分析更为全面。

2 极化敏感性分析

为了研究机身侧棱的极化特性，在电磁波频率为1.0 GHz时，分别对HH极化和VV极化两种条件进行仿真，如图2所示(主要考察方位角为0°～45°区间)。

从图2可以看出：机身侧棱在HH极化条件下的RCS明显高于VV极化条件下的RCS。通常认为，对于边缘类目标，电场方向平行于边缘时，RCS较大[5]，由此可以解释机身侧棱对HH极化更为敏感的原因。

为了定量对比两种极化的RCS，统计峰值、波峰宽度、旁瓣均值如表1所示。

表1 HH极化与VV极化条件下RCS对比

从表1可以看出：与VV极化相比，HH极化条件下RCS峰值大8.5 dB，波峰宽度大4°，旁瓣均值大5.8 dB，三项对比指标均是HH极化时较大。由此可见，机身侧棱在HH极化情况下隐身问题更为严重，需重点关注HH极化方式。

基于上述结论，本文后续计算只考虑HH极化情况。

3 频率敏感性分析

监视警戒雷达为飞机重要威胁之一，主要作用在低频，因此，重点关注低频时机身侧棱的电磁散射特点，分别计算电磁波频率为0.5、0.8、1.0、2.0、3.0、4.0 GHz时的RCS。以棱边长度5.00 m作为模型特征尺寸，则在上述频率下模型特征尺寸分别为8.3λ、13.3λ、16.7λ、33.3λ、50.0λ、66.7λ(λ为电磁波波长)。统计仿真结果如表2所示。

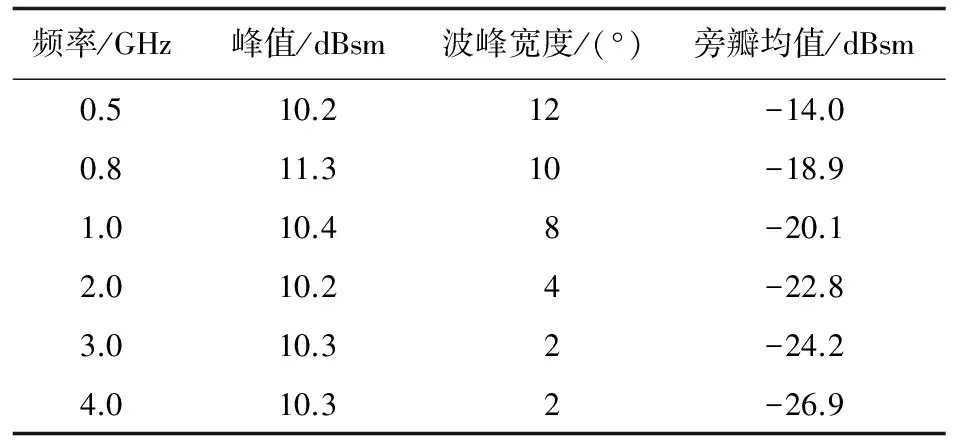
表2 不同电磁波频率下RCS对比

从表2可以看出：①峰值对频率不敏感，频率在0.5～4.0 GHz之间变化时，峰值变化量只有1.1 dB；桑建华[5]指出，直边缘垂直入射时，散射的频率依赖关系为f0，即垂直入射时直边缘RCS随频率变化较小，由此可以解释机身侧棱RCS峰值变化不大的原因。②波峰宽度对频率比较敏感，波峰宽度随频率变化曲线如图3所示，可以看出：频率越低波峰宽度越大，0.5 GHz时波峰宽度比4.0 GHz时大10°。③旁瓣均值对频率比较敏感，旁瓣均值随频率变化曲线如图4所示，可以看出：频率越低旁瓣均值越大，0.5 GHz时旁瓣均值比4.0 GHz时大13.0 dB。

4 几何参数敏感性分析

机身侧棱几何参数很多，包括棱边长度、棱边厚度以及机身剖面参数。重点研究棱边长度、棱边厚度以及剖面参数中上、下表面的切线夹角(棱边尖劈角)对RCS的影响规律。对于每一项几何参数，建立7组变参数模型并计算RCS，研究电磁散射对上述几何参数的敏感性。

仿真中重点考虑的是L波段(电磁波频率1.0 GHz)时的情况。

4.1 棱边长度影响

建立棱边长度分别为2～8 m的变参数模型，共7组，此时模型尺寸分别为6.7λ～26.7λ。计算RCS并统计结果如表3所示。

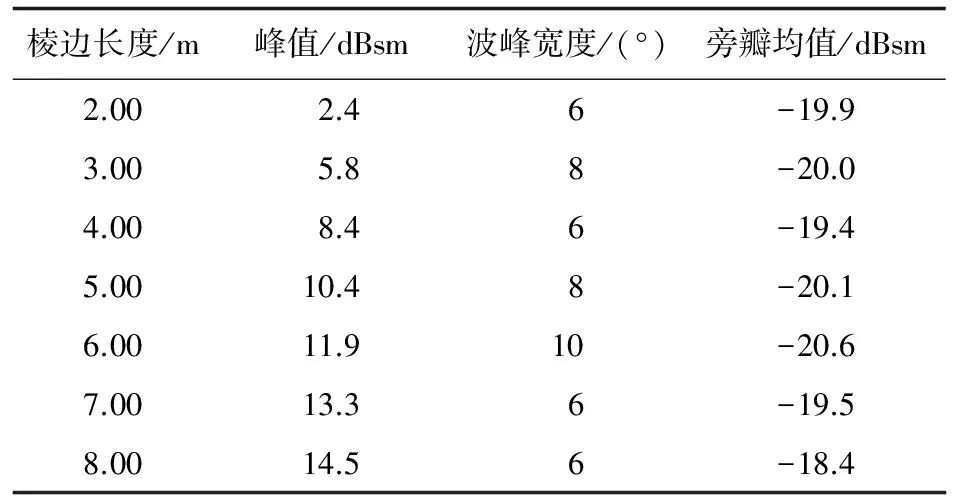
表3 不同棱边长度RCS对比

从表3可以看出：①峰值对棱边长度比较敏感，其随棱边长度的变化曲线如图5所示，可看出棱边长度越长，RCS峰值越大，棱边长度为8 m时比棱边长度为2 m时的RCS峰值高12.2 dB；桑建华[5]指出，直边缘垂直入射时，散射的尺寸依赖关系为L2，即垂直入射时直边缘RCS随尺寸变化较大，由此可以解释机身侧棱RCS峰值随长度增加而增加的原因。②波峰宽度和旁瓣均值对棱边长度不敏感，棱边长度在2～8 m之间变化时，波峰宽度变化量仅为4°，旁瓣均值变化量仅为2.2 dB。

4.2 棱边尖劈角影响

保持下表面切线角度为15°不变，改变上表面切线角度θ，角度分别为10°～90°(如图6所示)，共9组变参数模型。由于下表面切线角度保持不变，棱边尖劈角和上表面切线角度变化趋势一致，在分析规律时可以用上表面切线角度来表征棱边尖劈角。

RCS统计结果如表4所示。

表4 不同棱边尖劈角RCS对比

从表4可以看出：

①RCS峰值对棱边尖劈角比较敏感，其随上表面切线夹角的变化曲线如图7所示，可以看出棱边尖劈角越大，RCS峰值越大，上表面切线角度为90°时比10°时的RCS峰值增加10.5 dB；棱边尖劈角越大，棱边散射越接近镜面散射，因此RCS峰值越大。

②旁瓣均值对棱边尖劈角比较敏感，其随上表面切线夹角的变化曲线如图8所示，可以看出棱边尖劈角越大，旁瓣均值越大，上表面切线角度为90°时比10°时的旁瓣均值增加10.1 dB。

③波峰宽度对棱边尖劈角不敏感，棱边尖劈角变化时波峰宽度基本不变。

综上所述，棱边尖劈角增大，不仅会引起RCS峰值增加，也会引起旁瓣均值增大。

4.3 棱边厚度影响

上述计算中，棱边均为尖劈状，厚度为0 m，而实际生产中，0 m的边缘工艺上难以实现，为了保证可加工性，尖劈边缘需有一定厚度。因此，本节研究棱边厚度带来的影响。

保持棱边长度、机身剖面不变，改变棱边厚度d，如图9所示，使其分别为0.001～0.030 m，共10组变参数模型。仅考虑L波段的情况，此时电磁波波长λ为0.3 m，棱边厚度分别为(1/300)λ～(1/10)λ。RCS统计结果如表5所示。

表5 不同棱边厚度RCS对比

从表5可以看出：RCS峰值、波峰宽度、旁瓣均值对棱边厚度均不敏感；棱边厚度在(1/300)λ～(1/10)λ之间变化时，RCS峰值变化量仅1.7 dB，波峰宽度变化量仅4°，旁瓣均值变化量仅1.2 dB。

5 结 论

(1) 机身侧棱HH极化条件下比VV极化条件下隐身性能差。

(2) RCS峰值对棱边长度及棱边尖劈角比较敏感，棱边长度越长或棱边尖劈角越大，RCS峰值越大。

(3) 波峰宽度对频率比较敏感，频率越低波峰宽度越大。

(4) 旁瓣均值对频率及棱边尖劈角比较敏感，频率越低或棱边尖劈角越大，旁瓣均值越大。

(5) 在电磁波频率为1.0 GHz时，RCS对棱边厚度不敏感，厚度在1～30 mm之间变化时，RCS变化不大。

[1] 武哲, 仲聪颖. 低散射等剖面机身影区后向绕射机理分析[J]. 航空学报, 1994, 15(12): 1520-1523. Wu Zhe, Zhong Congying. The mechanism analysis for the backward diffraction on shadow area of equal-section fuselage having low radar cross section[J]. Acta Aeronautica et Astronautica Sinica, 1994, 15(12): 1520-1523.(in Chinese)

[2] 李南. 外形设计对飞机隐身性能影响分析[J]. 电讯技术, 2007, 47(5): 153-155. Li Nan. Analysis of contour design effects on fighter stealth performance[J]. Telecommunication Engineering, 2007, 47(5): 153-155.(in Chinese)

[3] 杨劼, 戴全辉, 黄兴军. 一种基于参数化建模的飞行器隐身外形设计优化方法[J]. 战术导弹技术, 2009(2): 1-5. Yang Jie, Dai Quanhui, Huang Xingjun. An approach to stealth shape design and optimization for flying vehicle based on parametric modeling[J]. Tactical Missile Technology, 2009(2): 1-5.(in Chinese)

[4] 白振东, 刘虎, 武哲. 低可探测机身参数化造型与优化[J]. 北京航空航天大学学报, 2007, 33(12): 1391-1394. Bai Zhendong, Liu Hu, Wu Zhe. Parametric modeling and optimization of low observability fuselage in aircraft conceptual design[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(12): 1391-1394.(in Chinese)

[5] 桑建华. 飞行器隐身技术[M]. 北京: 航空工业出版社, 2013: 63,66,73. Sang Jianhua. Low-observable technologies of aircraft[M]. Beijing: Aviation Industry Press, 2013: 63,66,73.(in Chinese)

[6] 阮颖铮. 雷达截面与隐身技术[M]. 北京: 国防工业出版社, 1998: 110-125. Ruan Yingzheng. Radar cross section and low-observable technologies[M]. Beijing: National Defense Industry Press, 1998: 110-125.(in Chinese)

[7] 姬金祖, 王岩, 黄沛霖, 等. 基于矩量法的机身截面电磁散射特性分析[J]. 航空工程进展, 2013, 4(1): 37-42. Ji Jinzu, Wang Yan, Huang Peilin, et al. Study on electromagnetic scattering characteristics of fuselage section based on method of moment[J]. Advances in Aeronautical Science and Engineering, 2013, 4(1): 37-42.(in Chinese)

[8] 张考, 马立东. 军用飞机生存力与隐身设计[M]. 北京: 国防工业出版社, 2002: 224-238. Zhang Kao, Ma Lidong. Military aircraft survivability and stealth design[M]. Beijing: National Defense Industry Press, 2002: 224-238.(in Chinese)

[9] 李启鹏, 王和平, 潘志雄, 等. 曲面机身剖面参数设计与隐身性能优化[J]. 计算机仿真, 2011, 28(1): 98-102. Li Qipeng, Wang Heping, Pan Zhixiong, et al. Section parameters design of the curved surface fuselage and stealth performance optimization[J]. Computer Simulation, 2011, 28(1): 98-102.(in Chinese)

[10] 张考, 张云飞, 马东立, 等. 飞行器对雷达隐身性能计算与分析[M]. 北京: 国防工业出版社, 1997. Zhang Kao, Zhang Yunfei, Ma Lidong, et al. Computation and research on low-observable performance of aircraft[M]. Beijing: National Defense Industry Press, 1997.(in Chinese)

[11] 聂在平. 目标与环境电磁散射特性建模——理论、方法与实现(应用篇)[M]. 北京: 国防工业出版社, 2009. Nie Zaiping. Modeling of electromagnetic scattering characteristics of target and environment-theory, method and realization[M]. Beijing: National Defense Industry Press, 2009.(in Chinese)

[12] 张扬, 艾俊强, 王健, 等. 倾斜双垂尾L波段电磁散射特点分析[J]. 电讯技术, 2015, 55(11): 1260-1265. Zhang Yang, Ai Junqiang, Wang Jian, et al. L-band electromagnetic scattering characteristic analysis of vertical fin[J]. Telecommunication Engineering, 2015, 55(11): 1260-1265.(in Chinese)

[13] 王健, 崔力, 柴建忠. 基于多层快速多极子算法的某隐身飞机RCS特性分析[C]∥第四届中国航空学会青年科技论坛文集. 北京: 中国航空学会, 2010: 193-199. Wang Jian, Cui Li, Chai Jianzhong. RCS analysis of a stealth fighter Based on multi-level fast multipolealgorithm[C]∥Conference Proceeding of the 4th CSAA Youth Science and Technology Form. Beijing: CSAA, 2010: 193-199.(in Chinese)

[14] 胡俊, 聂在平, 王军, 等. 三维电大目标散射求解的多层快速多极子方法[J].电波科学学报, 2004, 19(5): 509-524. Hu Jun, Nie Zaiping, Wang Jun, et al. Multilevel fast multipole algorithm for solving scattering from 3-D electrically large object[J]. Chinese Journal of Radio Science, 2004, 19(5): 509-524.(in Chinese)

[15] 刘战合, 田秋丽, 周钧, 等. 基于MLFMA 的飞行器电磁散射特性分析[J]. 合肥工业大学学报: 自然科学版, 2008, 31(12): 2044-2048. Liu Zhanhe, Tian Qiuli, Zhou Jun, et al. Analysis of scattering characteristics of aircrafts based on MLFMA[J]. Journal of Hefei University of Technology: Natural Science, 2008, 31(12): 2044-2048.(in Chinese)

(编辑：赵毓梅)

Analysis on Electromagnetic Scattering Characteristics of Fuselage Lateral Edge on Stealth Aircraft

Zhang Yang, Ai Junqiang, Wang Jian, Zhang Weiren

(The First Aircraft Institute, Aviation Industry Corporation of China, Xi’an 710089, China)

It is of importance to study the electromagnetic scattering characteristics of the lateral edges on stealth aircraft which is one of the dominant scattering sources for the lateral radar threats. Multilevel fast multipole method(MLFMM) is used to calculate the radar cross section(RCS) of the edge at different azimuth angles after the geometric model has been built. The magnitude and the width of the peak and the average value of the sidelobe are three important values to be evaluated and they are compared with each other at different polarization methods and frequencies. Sensitivities of the RCS to the geometric parameters, including length, angle and thickness of the edge, are also studied. The results show that the magnitude of the peak is sensitive to the length and the angle, the width of the peak is sensitive to the frequency, and the average value of the sidelobe is sensitive to frequencies and the angle.

stealth aircraft; edge; electromagnetic scattering; RCS

2016-11-11；

2017-01-13

张扬,zy_buaa@163.com

1674-8190(2017)01-017-06

V218

A

10.16615/j.cnki.1674-8190.2017.01.003

张 扬(1987-)，男，硕士，工程师。主要研究方向：飞机总体设计。

艾俊强(1964-)，男，硕士，研究员。主要研究方向：飞机总体与气动设计。

王 健(1980-)，男，硕士，高级工程师。主要研究方向：飞机总体设计。

张维仁(1989-)，男，硕士，助理工程师。主要研究方向：飞机总体设计。