某型联翼布局无人机的气动计算与分析

惠哲，沈海军

(同济大学 航空航天与力学学院，上海 200093)

某型联翼布局无人机的气动计算与分析

惠哲，沈海军

(同济大学 航空航天与力学学院，上海 200093)

与常规布局飞机相比，联翼布局飞机具有结构重量轻、抗弯扭强度大、诱导阻力低、升力系数大和稳定性好等优点。介绍一种高效的数值模拟方法，完成对某型联翼布局无人机气动特性的初步计算与分析。基于商业软件ANSYS，整个研究过程着重于从网格建模、全机流场模拟、气动模拟数据分析三个方面，探索该型无人机纵向、横向和航向的气动特性以及主操纵面的操纵效率，实现对该型无人机稳定性和操纵性能的表征与评估。结果表明：无人机升降舵偏角的变化不影响无人机的握杆静稳定度，并且在0°～25°的升降舵偏角(下偏)范围内，升降舵偏角与升降舵的升力系数基本呈线性变化；在-4°～12°的迎角范围内，随着迎角的不断增大，该型无人机的横向静稳定性水平越大；两个垂直翼和垂尾是产生航向静稳定性的主要部件。

联翼布局；数值模拟；气动特性；放宽静稳定性；舵面效率

0 引 言

联翼布局飞机(Joined-wing Aircraft)的机翼通常由后掠前翼和前掠后翼两部分组成，后翼翼尖与前翼翼尖或前翼中部相连，构成菱形的框架机翼。如果前翼在上，后翼在下，这种结构称为“正交错”(Positive Stagger)；反之，则称为“负交错”(Negative Stagger)[1]。

联翼布局飞机的研究最早始于20世纪70年代，由J.Wolkovitch[2]提出。随后，国内外陆续对联翼布局飞机的气动、结构、重量等方面进行了系统的研究，与常规布局飞机相比，联翼布局飞机具有抗弯扭强度高、结构重量低、机翼的有效展弦比大、诱导阻力小等优点。联翼布局飞机由于其显著的升阻特性优势在世界范围内受到了越来越多的关注，此类布局的气动特性研究方法主要包括N-S方程、欧拉方程、涡格法、风洞实验和模型试飞等。其中， J.Wolkovitch[3]和J.Corneille[4]贡献最为突出，二者先后对联翼布局飞机开展了一系列风洞实验及对比分析研究，研究表明联翼布局飞机相对传统布局飞机具有最大升阻比大、诱导阻力小、稳定性好和结构重量低等优势。王延奎等[5]采用求解雷诺平均N-S方程的方法完成了对某亚音速联翼布局飞机气动特性及其绕流流场的研究。R.K.Nangia等[6]通过求解欧拉方程对联翼布局飞机进行了诱导阻力和操稳特性的计算与分析。为了讨论某型联翼布局飞机的外形参数变化对稳定性的影响，郭卫刚等[7]采用涡格法对其进行了研究。李军等[8]对联翼布局飞机的机翼、机身、控制面以及起落架布置等方面进行了概念设计研究。

目前，国内外对联翼布局飞机气动特性的研究仍处于探索与发展阶段，对联翼布局失速特性、舵面效率等黏性作用强烈的边界气动特性的研究仍鲜少报道。本文采用数值模拟的方法完成对某型联翼布局无人机全机气动特性的初步计算，探索该型无人机纵向、横向和航向的气动特性以及主操纵面的操纵效率，进而实现对该型无人机稳定性和操作性能的表征与评估。

1 模型基本参数

某型无人机采用“负交错”构型，机身长4.2 m，采用有弯度流线型机身，如图1所示。一对全动鸭翼与机身相连接，鸭翼的翼展为2.166 m，稍根比为0.488，鸭翼前缘后掠角为22.5°。前翼为下单翼，其翼展为4.596 m，稍根比为0.539，前翼前缘后掠角为21.7°、上反角为4.8°。后翼与垂尾的顶端相连接，其翼展为4.806 m，稍根比为1.000，后翼前缘前掠角为11.4°、下反角为3.08°。后翼翼尖和前翼翼尖分别与两个垂直机翼相连接，从而形成菱形框架机翼结构。升降舵位于后翼后缘内侧，升降舵的翼展占整个后翼翼展的20.8%，其翼弦占整个后翼弦长的45.5%。副翼位于前翼后缘外侧，副翼的翼展占整个前翼翼展的17.4%，其翼弦占整个前翼弦长的22.6%。无人机的两个方向舵分别位于左、右垂直翼的后缘。该型无人机的鸭翼、前翼和后翼均采用非对称高升力翼型。此外，该型无人机被设定为低空低速无人机，其飞行速度区间为100～200 km/h，飞行高度在500 m左右。全机计算坐标系定义x轴指向机头，y指向右侧机翼，z轴垂直向下。舵面偏转方向定义如下：升降舵下偏为正；右副翼下偏，左副翼上偏为正；方向舵左偏为正。无人机的俯仰力矩、滚转力矩和偏航力矩方向均遵循右手螺旋法则。

2 数值计算

2.1 数值计算方法介绍

采用ANSYS FLUNET对该型无人机进行全机流场模拟。控制方程为非定常雷诺平均N-S方程。不可压湍流计算的基本方程为平均流连续方程：

(1)

平均流动量方程为

(2)

湍流模型为Spalart-Allmaras(S-A)一方程模型[9]，主要用于航空领域外部流场模拟，同时在涡轮机械中也得到了广泛的应用。S-A模型常用于计算墙壁束缚流动，解决因湍流动黏滞率而修改的数量方程，对低雷诺数流模型的计算具有较好的效果。此外，从计算经济性角度来看，S-A模型是FLUENT中最经济的湍流模型。

S-A模型运输方程为

(3)

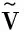
2.2 网格建模

基于商用网格生成软件ANSYSICEMCFD进行无人机网格建模，采用Delaunay算法生成非结构网格，此算法是一种自下而上(Bottom-up)的网格生成方法。首先，在气流的出入口、对称面、压力远场以及无人机的表面生成高质量的三角形网格；然后，在无人机表面的三角形网格(壳网格)基础上拉伸成棱柱网格(边界层网格)；最后，用四面体网格填充棱柱网格和压力远场之间的间隙。此外，为了获得更精确的数值模拟数据，在机头、机翼的前后缘以及机翼与机身连接处等区域进行局部网格加密，并在机翼尾缘附近创建加密区(机翼尾缘附近的流动对升阻力系数的影响较大)。网格模型共计1 172.3万个网格单元，如图2所示。

2.3 全机流场模拟

利用商业CFD分析软件ANSYSFLUENT进行该型无人机的全机流场模拟。该型联翼布局无人机飞行高度取500m左右，飞行速度低于0.3Ma；在此高度和速度下，绕该型无人机流场中各点的压力和密度的变化甚微，即空气的压缩性可以忽略。换句话说，对于流速不超过0.3Ma的低速气流，气流的体积弹性模数趋于无穷大或密度等于常数。

根据上述假设，对FLUENT中的求解器设置如下：求解器类型选为基于压力(Pressure-based)；速度方程选为绝对速度(AbsoluteVelocity)；时间求解类型选为稳态流动(SteadyFlow)。此外，流场的边界条件选为压力远场边界条件，该边界条件用于设定无限远处的自由来流条件，其主要设置项为自由来流马赫数和静参条件。为了满足无限远这一要求，压力远场必须放置在距离无人机网格模型足够远的地方。一般而言，在飞机的气动计算中，推荐压力远场边界到飞机的距离大约为飞机特征长度的20倍左右。应注意，压力远场边界条件要求气体模型必须为理想气体。本文建立一个至少为无人机特征长度30倍圆周之外的长方体压力远场，如图3所示。

通过改变流场入口和出口的气流迎角α、气流侧滑角β、自由来流速度V∞以及该型无人机的舵面偏角(升降舵、副翼和方向舵)，获得该型无人机纵向、横向和航向的相应气动模拟数据。当V∞=34.71m/s，α=3°时，无人机全机静压分布如图4所示，无人机速度迹线如图5所示。

从图4可以看出：无人机机头以及机翼前后缘处的压力分布最大。无人机的升力源于机翼上下表面气流的速度差所导致的压力差。由于无人机的鸭翼位于其联翼之前，鸭翼下洗会改变气流，影响联翼的流场，并且鸭翼和联翼所产生的涡流会相互影响[10]。

从图5可以看出：鸭翼激起的涡流[11]混合着快速移动的气流通过前翼内侧的上表面，额外提供气流能量，一定程度上增加了无人机的升力。

无人机各部分升力系数的贡献如表1所示，可以看出：在巡航迎角(α=3°)下，该型无人机的鸭翼、翼身组合体(由于该型无人机翼展/机身直径比相对较小，故前翼和机身之间的相互影响较大，因此采用翼身组合体进行数值模拟计算)和后翼均产生正的升力，其中翼身组合体对全机升力系数的贡献最大，约占全机升力系数的84.82%。

表1 无人机各部分升力系数的贡献

3 气动特性结果分析

3.1 无人机纵向气动特性结果分析

无人机的雷诺数计算公式为

(4)

式中：ρ为空气密度；V∞为自由来流速度；d为飞机的平均气动弦长；μ为动力黏性系数。

假设该型无人机在同一高度(500 m左右)以不同的速度V∞飞行(低于0.3Ma)，即对于相同的空气密度ρ和动力黏性系数μ，该型无人机的雷诺数随着自由来流速度的增大而增大。因此，对于低速流动，流动在某一固定方向上的气动系数仅为雷诺数的函数[12]。

不同速度下无人机的纵向气动特性曲线如图6所示。

从图6(a)可以看出：在该型无人机迎角α较小时，升力系数CL随迎角α呈线性变化。

从图6(b)可以看出：该型无人机的阻力系数CD随迎角α呈非线性变化。此外，阻力在任何形状的气动体上都由摩擦阻力和压差阻力两部分组成，且翼型的型阻系数又与黏性有关，因此阻力系数CD的大小受Re的影响。

纵向气动数值计算结果如表2所示。

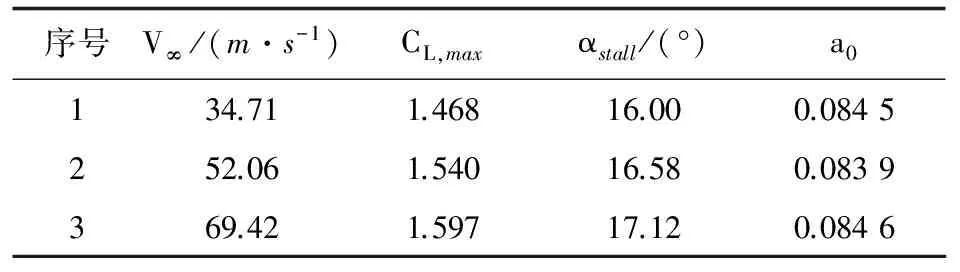
表2 纵向气动数值计算结果

从表2可以看出：升力线斜率a0与V∞基本无关，而最大升力系数CL,max和失速迎角αstall均与V∞有关。由式(4)可知，对于在相同高度(低空)以不同速度(低于0.3Ma)飞行的同一无人机，自由来流速度与Re成正比，表明该型无人机的最大升力系数和失速迎角均与雷诺数有关。

另外，由于雷诺数是惯性力与黏性力之比的相似参数，从而推断出最大升力系数与失速迎角均受黏性的影响。雷诺数越大，流经机翼表面的边界层会越早地从层流边界层过渡为紊流边界层[13]，而紊流边界层不容易从机翼表面分离，故失速迎角前移，该型无人机更不易失速。

不同升降舵偏角下无人机升力系数随迎角的变化曲线如图7所示。

从图7可以看出：无人机升降舵偏角δe(下偏)的增加，促使无人机升力系数增大。

升降舵偏转所引起的后翼升力系数增量可表示为

(5)

式中：ah为无人机后翼的升力线斜率；αh为无人机后翼的有效迎角；τ为升降舵效率，即升降舵偏转单位角度相当于后翼迎角增量；Δδe为升降舵偏角的变化量。

由气动数值模拟计算得到ah=0.078 216 9，τ=0.255 825。带入式(5)得到CL,h=0.02Δδe，即升降舵每下偏1°，相当于后翼升力系数增加0.02。

无人机升降舵的气动模拟结果如表3所示，可以看出：无人机的升降舵偏角δe在25°范围内，舵偏角与气动力基本呈线性，即

(6)

式中：CL,e为升降舵偏转所产生的升力系数。

表3 升降舵升力系数的数值计算结果

该型无人机纵向俯仰力矩系数随迎角的变化曲线如图8所示(其他速度的变化曲线与之类似)。

从图8可以看出：

①无人机的俯仰力矩系数变化曲线斜率CMα>0且零升俯仰力矩系数CM0<0，表明该型无人机纵向静不稳定，即无人机的焦点位于其重心之前。采用这种放宽静稳定度(Relaxed Static Stability，简称RSS)布局[14]的方法设计无人机，可以有效地降低配平阻力损失。换句话说，为了提高无人机性能，对静稳定性进行了折中。放宽静稳定度后，无人机的静裕度为

②一小段迎角α区间内俯仰力矩系数的下降与达到失速迎角所引起的无人机升力显著下降有关。此外，该型无人机升降舵偏角δe的变化引起CM-α曲线的上下平移而不改变CM-α曲线的斜率。换句话说，该型无人机的δe不影响其握杆静稳定度，并能在有效的升降舵偏角δe范围内(不超过升降舵的最大偏角)完成对无人机所有允许迎角下俯仰力矩系数的配平。

3.2 无人机横向气动特性结果分析

当V∞=52.06m/s时，该型无人机的横向气动特性曲线如图9所示。

从图9(a)可以看出：正侧滑角对应负的滚转力矩系数，而负侧滑角对应正的滚转力矩系数，且该型无人机的滚转力矩系数Cl与侧滑角β近似呈线性关系。由横向静稳定性判据可知

(7)

式中：Clβ为横向静稳定性导数。

式(7)表明该型无人机横向静稳定，即拥有抵抗滚转扰动的固有能力。在-4°～12°的迎角范围内，无人机的迎角α与横向静稳定性导数Clβ成反比，即随着迎角α的不断增大，无人机的横向静稳定性水平越大(抵抗滚转扰动的能力越强)。这是由于无人机的升力L主要由其鸭翼和翼身组合体提供，而机翼的后掠角Λ起横向静稳定性作用，机翼后掠角Λ对无人机横向静稳定性的贡献为

(8)

式中：c(y)为机翼剖面弦长；SW为机翼面积。

由式(8)可知升力系数CL与无人机的横向静稳定性导数Clβ成反比。

从图9(b)可以看出：正的副翼偏角δa(差动)所产生的Cl为负，因此该型无人机副翼操纵效率Clδa<0。

从图9(c)可以看出：无人机在巡航迎角下，对应不同的副翼偏角δa，滚转力矩系数Cl随侧滑角β的变化曲线上下平移。由于Clδa为负值，故当δa>0时，曲线下移；反之，曲线上移。此移动量反映了副翼操纵效率的大小。

当β=0°时，副翼效率数值计算结果如表4所示，可以看出：在-4°～12°的迎角范围内，该型无人机的副翼效率Clδa随着迎角α的增大而增大。

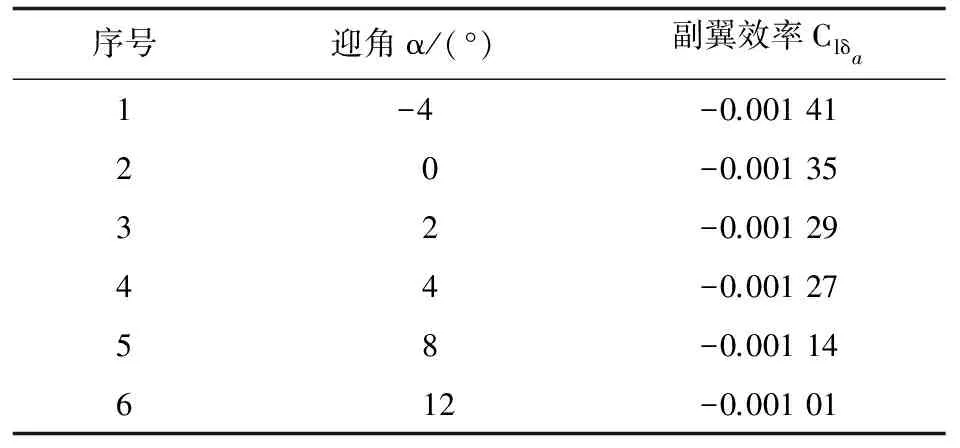
表4 当β=0°时副翼效率数值计算结果

3.3 无人机航向气动特性结果分析

当α=3°时，无人机偏航力矩系数随侧滑角β的变化曲线如图10所示。由于无人机在巡航迎角下飞行具有较好的性能，并且无人机的侧力系数和偏航力矩系数与迎角α的关系不大，故本文仅选取巡航迎角下无人机的偏航特性曲线。

从图10可以看出：

①正侧滑角对应正的偏航力矩系数，负的侧滑角对应负的偏航力矩系数。根据航向静稳定性要求可知：

(9)

式中：Cnβ为偏航静稳定性导数。

式(9)表明该无人机航向静稳定，即无人机有迎着相对风方向的趋势。产生一定的侧滑角β所需的方向舵偏角计算公式为

(10)

由式(10)可知：航向静稳定性越高，为了产生一定的侧滑角需要的方向舵偏角越大。

②无人机在巡航迎角下，对应不同的方向舵偏角δr，偏航力矩系数Cn随侧滑角β的变化曲线上下平移。由于方向舵左偏为正，产生负的偏航力矩系数，故Cnδr为负值。当δr>0时，曲线下移；反之，曲线上移。根据此移动量的大小，推得无人机在巡航迎角下，其方向舵的操纵效率Cnδr=-0.001 089 5。

当该型无人机的自由来流速度V∞=52.06 m/s，迎角α=3°时，无人机各主要部分所产生的偏航静稳定性导数数值计算结果如表5所示。

表5 无人机各部分偏航静稳定性导数数值计算结果

从表5可以看出：该型无人机的两个垂直翼和垂尾是产生航向静稳定性的主要部件。

4 结 论

(1) 该型无人机纵向静不稳定，通过适当放宽无人机的纵向静稳定度，可以很大程度上减小无人机纵向的配平阻力，从而使无人机更加灵活。此外，无人机升降舵偏角δe不影响其握杆稳定度，并能在有效升降舵偏角δe范围内(不超过升降舵的最大偏角)完成对无人机所有允许迎角下俯仰力矩系数的配平。

(2) 该型无人机横向静稳定，即拥有抵抗滚转扰动的固有能力。机翼的后掠角Λ起横向静稳定性作用。此外，在-4°～12°的迎角范围内，该型无人机的横向静稳定性水平和副翼效率均随着迎角的增大而增大。

(3) 该型无人机航向静稳定，即无人机有迎着相对风方向的趋势。无人机的两个垂直翼和垂尾是产生航向静稳定性的主要部件。

综上所述，为了飞机或无人机能安全飞行，必须能够配平，且具有足够的纵向、横向与航向稳定性。为了改善性能，飞机或无人机的稳定性经常需要折中处理，同时需要综合考虑飞机或无人机的操纵性与稳定性。为了保证飞行安全，此类飞机或无人机必须提供闭环稳定性。

[1] 郑诚行. 连翼布局飞机及探测无人机研究进展[J]. 飞行力学, 2006, 24(4): 1-5. Zheng Chengxing. Research and development on joined wing aircraft and sensorcraft[J]. Flight Dynamics, 2006, 24(4): 1-5.(in Chinese)

[2] Wolkovitch J. The joined wing: an overview[J]. Journal of Aircraft, 1986, 23(3): 161-178.

[3] Wolkovitch J. Low-speed wind tunnel test on joined wing and monoplane configurations. Volume 1. analysis of results[R]. ACA-82-1, 1982.

[4] Corneille J. Wind tunnel investigation of joined wing configurations[D]. Ohio: Air Force Institute of Technology, 1999.

[5] 王延奎, 单继祥, 田伟, 等. 联翼布局俯仰力矩非线性变化特性的数值模拟[J]. 北京航空航天大学学报, 2012, 38(7): 862-866. Wang Yankui , Shan Jixiang , Tian Wei, et al. Investigation on non-linear characteristic of pitching moment of joined wing configuration aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7): 862-866.(in Chinese)

[6] Nangia R K, Palmer M E, Tilmann C P. Unconventional high aspect ratio joined-wing aircraft with aft- & forward-swept wing-tips[R]. AIAA-2003-0605, 2003.

[7] 郭卫刚, 贾忠湖, 康小伟. 某联接翼飞机外形参数变化对稳定性影响的研究[J]. 飞机设计, 2007, 27(2): 37-40. Guo Weigang, Jia Zhonghu, Kang Xiaowei. Impacts of aerodynamic configuration parameters on stabilities of joined-wing aircraft[J]. Aircraft Design, 2007, 27(2): 37-40.(in Chinese)

[8] 李军, 李占科, 宋笔锋. 联翼高空长航时无人机总体布局设计研究[J]. 飞行力学, 2009, 27(4): 1-4. Li Jun, Li Zhanke, Song Bifeng. Conceptual layout design of the joined-wing high-altitude-long-endurance UAV[J]. Flight Dynamics, 2009, 27(4): 1-4.(in Chinese)

[9] Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[C]∥30th aerospace sciences meeting and exhibit. USA: AIAA, 1992.

[10] Tu E L. Vortex-wing interaction of a close-coupled canard configuration[J]. Journal of aircraft, 1994, 31(2): 314-321.

[11] Zhang G, Yang S, Xu Y. Investigation of vortex interaction in canard-FSW configurations based on the numerical wind tunnel method[J]. Chinese Journal of Aeronautics, 2010, 23(3): 312-319.

[12] Anderson J D. Fundamentals of aerodynamics[M]. New York: McGraw-Hill, 1984.

[13] Marchman J F. Aerodynamic testing at low Reynolds numbers[J]. Journal of Aircraft, 1987, 24(2): 107-114.

[14] 王华友, 王维安, 高亚奎. 放宽纵向静稳定度飞机的平尾面积收益分析方法[J]. 航空学报, 2007, 28(2): 290-293. Wang Huayou, Wang Weian, Gao Yakui. Method to analyze horizontal tail area benefits of RSS aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(2): 290-293.(in Chinese)

(编辑：赵毓梅)

Aerodynamic Calculation and Analysis of a Joined-wing Unmanned Aerial Vehicle

Hui Zhe, Shen Haijun

(School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200093, China)

Joined-wing configuration has lower structural weight, higher torsional/flexural strength, smaller induced drag, bigger lift coefficient, and better stability than the normal one. An effective numerical simulation method for calculation and analysis of aerodynamic characteristics of a joined-wing unmanned aerial vehicle(UAV) is provided. The whole research process of the UAV based on commercial software ANSYS consists of grid modeling, simulations of the flow field of the UAV, analyses of the aerodynamic data. By means of exploring the longitudinal, lateral and directional stability of the UAV, control devices efficiency, the evaluation of the UAV flight performance are achieved. The results indicate that the variation of elevator deflection does not affect the stick-fixed static stability level of the UAV, and the lift coefficient of the elevator of the UAV increases linearly with downward elevator deflection angle in the range 0°～25°. The level of the lateral static stability of the UAV increases as the angle of attack increases in the range -4°～12°. The contribution of the directional stability of the UAV is dominated mainly by the two vertical wings and the vertical tail.

joined-wing configuration; numerical simulation; aerodynamic characteristics; relaxed static stability; control surfaces efficiency

2017-01-03；

2017-02-17

沈海军,shj@tongji.edu.cn

1674-8190(2017)01-001-08

V212.1

A

10.16615/j.cnki.1674-8190.2017.01.001

惠 哲(1992-)，男，硕士研究生。主要研究方向：飞行力学和飞机结构设计。

沈海军(1971-)，男，博士，教授。主要研究方向：飞行器设计、结构力学、纳米器件中的力学模拟与仿真等。