基于Lax差分格式的电力电缆故障测距仿真研究

马贵东, 王红艳， 朱建忠， 张鹏， 吴恒

(南京工程学院，江苏 南京　211167)

0　引　言

随着城市的发展，电缆的应用越来越广泛，但接踵而来的电缆故障也越来越频繁。为了更好地解决电缆故障问题，减少停电造成的经济损失，电缆故障的准确定位成为了亟待解决的关键问题。

目前，行波法是应用最为广泛的电缆故障测距方法，当行波在电缆中遇到阻抗不匹配点会发生波反射，根据发射的波形与反射的波形之间的时间差，结合电缆的行波速度以此求出电缆的故障距离或电缆全长，主要包括低压脉冲法、脉冲电压法、脉冲电流法以及二次脉冲法等[1]。但是，行波法得到的波形较为复杂，缺少经验的检修人员不能对波形进行准确的分析，本文通过模拟仿真行波法电缆故障得到故障波形，以此对检修人员进行理论培训，从而对故障距离有更好地把握。

另外，传输线方程本质是一阶双曲线型偏微分方程组，对于电缆传输线的时域分析，许多学者从数值方法对电缆的传输线方程进行分析。目前，对偏微分方程的分析方法主要有Upwind差分格式Lax差分格式、Lax-Wendroff格式[2-4]。Upwind是基于特征线的走向来选取差分格式的[5]，但是随着空间偏导数的数值越来越大，该差分格式的稳定性越差，而且产生的震荡越大，对于精度的影响也越来越大，另外Lax-Wendroff格式是二阶精度，出现间断点时，间断的过渡区太窄，不易于波形分析[6]。而对于Lax差分格式来说，采用中心差商的思想，截断误差小，而且产生的震荡小，精确度高。综合考虑，本文利用Lax差分格式对电缆传输线进行时域分析，模拟出电缆故障的情形，分析电缆传输线在各种故障下的情形，利用该差分格式来分析传输线方程，建立低压脉冲、脉冲电流法的测距模型，确定了首端末端的边界条件，模拟出了电缆发生故障时的情形，给出了故障点的差分方程，结合MATLAB得到波形，以此求出电缆故障距离。

1　Lax差分格式的建立

有限差分法的思想是把将连续的时间空间坐标离散后，得到时间空间的网格，在网格点上利用差商来代替方程中的微商，形成了某种差分格式，本文采用Lax差分格式[7-8]。根据每行所有网格上的节点的差分格式，得到线性代数方程组，再通过电缆首端和末端的边界条件，以及出现故障时，故障点处的差分格式，迭代求出所有节点的数值，包括电缆首端末端以及故障点处的电压电流的数值。

对于均匀传输线的一阶双曲线方程组[9]：

(1)

其中该方程组与时间和距离有关。首先将连续分布的时间和空间进行剖分，以此得到时间空间的网格图。其中时间步长设置为k，空间步长设置为h，设任意距离表示为xm，任意时间为tn，则时间空间网格上任意一点可以表示为(xm,tn)。

对于传输线方程中的电压电流对距离的偏导，用中心差商代替，即：

(2)

对于电压电流的时间偏导，采用向前差分，即：

(3)

(4)

结合方程组(1)，(2)，(3)，(4)，得到基于Lax的差分格式，即：

文献[3]利用傅里叶的方法分析了该差分格式的稳定性条件为：

(6)

2　电缆故障测距方法建模

2.1　低压脉冲法

如图1所示，是低压脉冲法的电路模型图。低压脉冲法是向电缆中注入一定宽度的低压脉冲，当行波遇到电阻不匹配点时会产生反射波形，根据入射波形与反射波形间的时间差，来计算得到故障距离。图1中，R0，G0，L0，C0为电缆的特性参数，Rf为故障点等效电阻。

图1　低压脉冲法电路模型图

低压脉冲法的首端条件，可以根据基尔霍夫定律来推导，即由图1可得，

(7)

其中令dx=h，dt=k，对电流的时间的导数采用向前差分，于是便可以得到低压脉冲法的首端边界条件，即：

(8)

另外，由电路图1可得，当m=M时处于电缆末端，即电缆末端满足：

(9)

将其带入Lax差分格式公式(5)，便可以得到低压脉冲法的末端条件，即：

(10)

当电缆在x处发生故障，如低压脉冲法模型电路图1所示，在x处接入故障的等效电阻Rf，由此根据基尔霍夫定理可以得到，故障点处的电压电流关系，即：

(11)

对时间导数采用向前差商，可得：

(12)

公式(12)就是电缆发生故障时，故障点的条件。

2.2　脉冲电流法

脉冲电流法电路模型如图2所示，G为球形间隙，C为高压储能电容，Us为交流电源，交流电源不断给电容充电，直到球形间隙G击穿，电容开始对电缆放电。球形间隙的击穿电压设为Ug，脉冲电流法的首端边界条件的推导，是以球形间隙G被击穿时开始的，也就是球形间隙被击穿后，电容上具有等于Ug大小的电压Uc。

图2　脉冲电流法电路模型图

在图2中，根据基尔霍夫定律，得：

(13)

对关于时间的导数采用向前差分进行离散，同时令dx=h，dt=k，即可以得到脉冲电流法的首端边界条件：

(14)

脉冲电流法的末端边界条件和低压脉冲法的相同，即为公式(10)。脉冲电流法的故障点条件同低压脉冲法的相同，即公式(12)，但是需要实时监测故障点是否被击穿，若故障点的电压大于故障点的击穿电压，则发生闪络故障，此刻故障点的关系式为：

(15)

对时间导数采用向前差分，得到：

(16)

即公式(16)为电缆故障点被击穿时的故障条件。

3　参数设置及仿真实现

在确定了测距方法的首端末端条件以及故障点的条件时，利用MATLAB编程[10]，其流程图如图3所示。

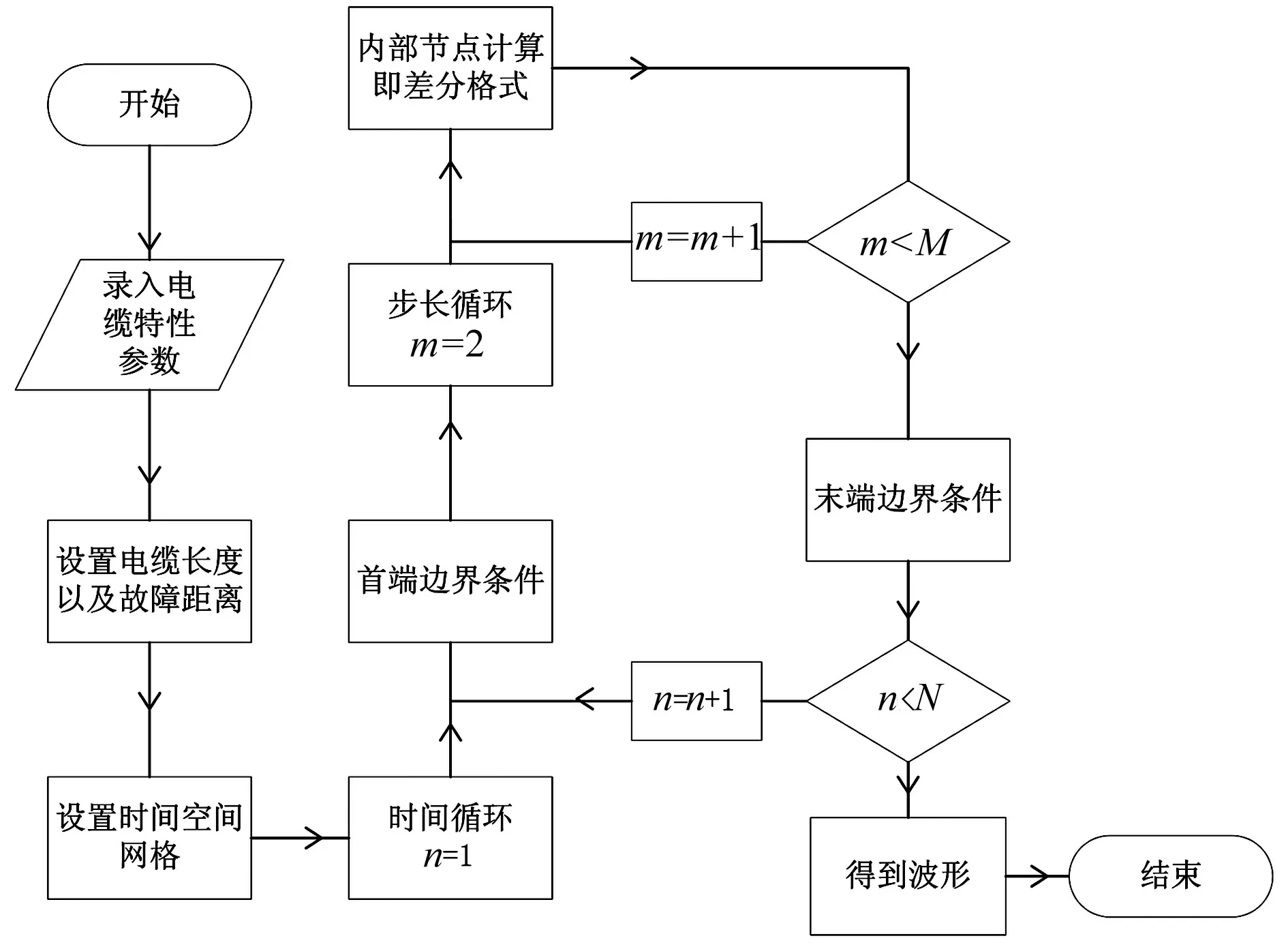
图3　算法流程图

设置电缆的分布参数为：

R0=3.256 8×10-5Ω/m,G0=8.132 5×10-12S/m

L0=122.8×10-9H/m,C0=329.60×10-12F/m

电缆全长L=800 m,电缆分成400段，即M=400段，设置故障距离x=400 m，设置仿真时间为T=50 μs。电缆行波速度为：

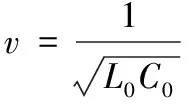
波阻抗为：

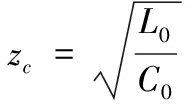
空间步长：

时间步长：

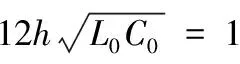
则得到的故障距离为：

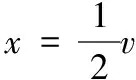
其中Δt=步长×步数。

3.1　低压脉冲法测距得到的波形及分析

设置低压脉冲幅度Us=10 V，电源内阻Rs=150，脉冲宽度τ=2 μs。如图4所示为低压脉冲法仿真得到的电缆无故障的首段电压U1的波形。在图4中，由于电缆末端开路，第一个脉冲为发射脉冲，第二个脉冲为反射脉冲，其极性与发射脉冲相同，且电压幅值增大，其后的反射波行逐渐衰减。图中t1=6 500，t2=13 000，t3=19 500，可得:

Δt=k×t1=k×(t2-t1)=k×(t3-t2)

电缆长度为：

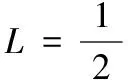
与实际设置的电缆长度相差6 m，误差小于1% 。

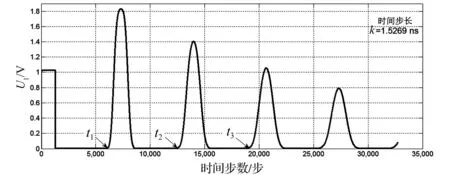
图4　低压脉冲法得到的电缆无故障波形

设置电缆的故障点电阻Rf=50 Ω时，电缆发生低阻故障，低压脉冲法仿真得到的电缆首端电压U1的波形，如图5所示。第一个波形是发射脉冲，第二个脉冲极性与发生脉冲相反，发生低阻或者短路故障，第三个脉冲为末端开路反射波形，与第一个脉冲波形极性相同，之后的故障点反射波形和电缆末端反射波逐渐衰减。在图5中，t1=3 100，t2=6 300，t3=12 600。电缆的故障距离：

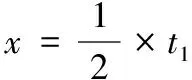
与实际设置的故障点400 m，相差21.33 m，误差为5%左右。仿真波形得到的电缆的长度为：

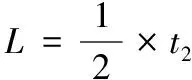
或

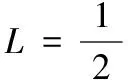
计算得769.56 m，与实际800 m相差21.44 m，误差为2%左右。

图5　低压脉冲法得到的电缆低阻波形

设置故障点的等效电阻Rf=700 Ω时，电缆发生高阻故障，低压脉冲法仿真得到的电缆首端电压U1的波形，如图6所示。第一个脉冲为发射脉冲，第二个波只有很小的一点，出现负极性，之后第三个波形为电缆末端反射波。对于高阻故障，用低压脉冲法来测距，波形不是很明显，只有很小的一部分，该类故障用个脉冲电流法测距效果更好。

图6　低压脉冲法得到的电缆高阻故障波形

3.2　脉冲电流法测距得到的波形及分析

脉冲电流法是在球形间隙G击穿时开始仿真的，此刻设置电容C的初始值为球形间隙的击穿电压Ug，故障点的临界击穿电压Uf=10 kV，高压储能电容C=3 μF。脉冲电流法是通过线性电流耦合器的电流I的波形来进行分析的。仿真可以得到电流首端电流的变化量I，其等价于线性耦合器得到的电流波形。

设置Ug=3 kV，故障点等效电阻Rf=700 Ω，故障点处的电压没有达到临界击穿电压，故障点没有被击穿，得到首端电流的变化量I的波形如图7所示。故障点没有被击穿，由于电缆末端开路，电流行波发生负极性反射，电容端相当于短路，电流行波发生正极性反射，即图7中正负交替的行波。在图7中，t1=14 200，t2=20 700，t3=27 300，可以得到电缆的长度:

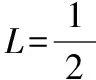
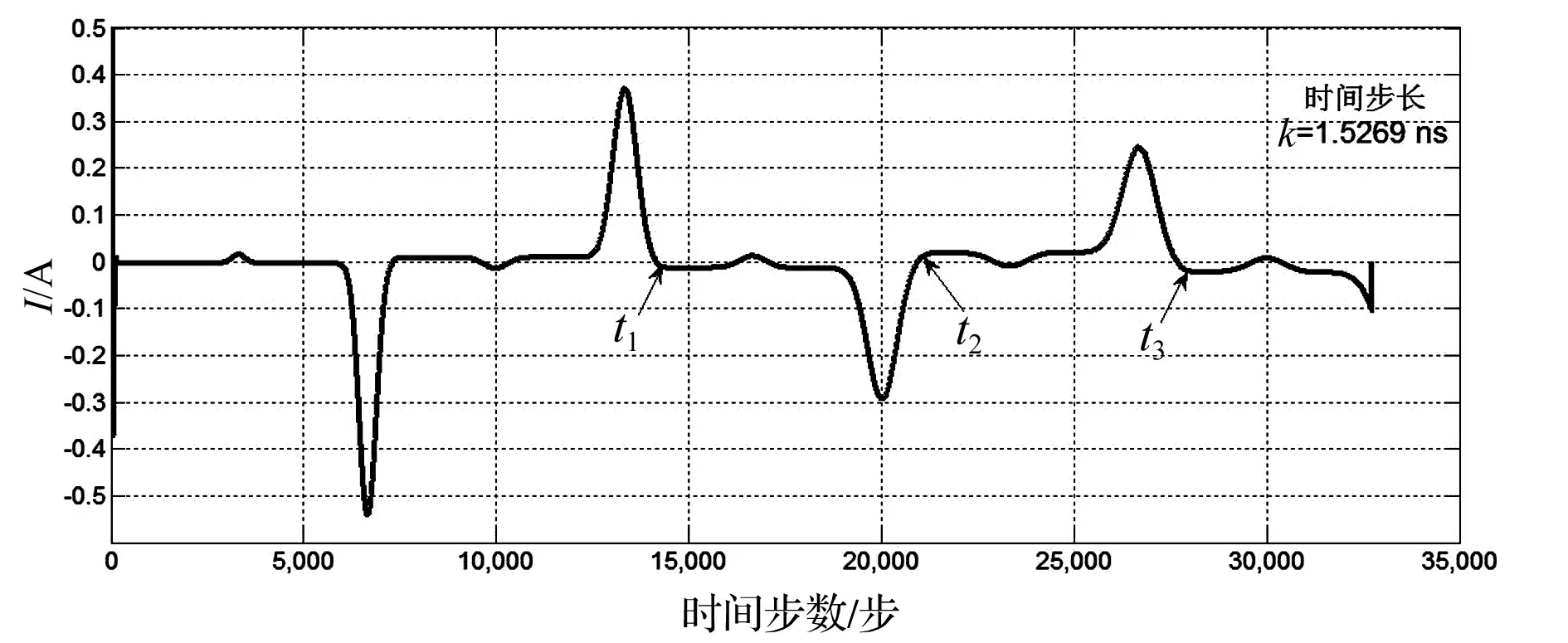
图7　脉冲电流法得到的故障点未击穿波形

设置Ug=3 kV，故障点等效电阻Rf=700 Ω，故障点处的电压达到临界击穿电压，故障点被击穿，得到首端电流的变化量I的波形如图8所示。由于故障点直接被击穿，相当于短路点，电流行波遇到时发生正极性反射，又由于电容端相当于短路，电流行波在此处也发生正极性反射，即如图中8的波形出现都是同极性波形，在图8中，t1=7 300，t2=10 500，t3=14 300，所得到的故障距离：

故障距离与设置的实际故障点距离400 m相差9.22 m，误差在2%左右。

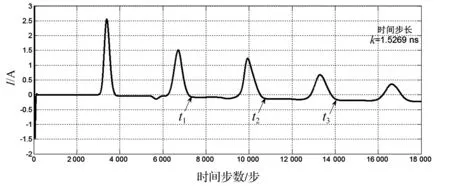
图8　脉冲电流法得到的故障点击穿波形

4　结束语

利用Lax差分格式进行电缆传输线的时域分析，根据仿真结果和实际设置的故障点相比较，误差相对较小，验证了Lax差分格式的可行性。建立在Lax差分格式的基础上得到的低压脉冲波形与脉冲电流波形，与文献[5]的Upwind的差分格式相比较，Lax的差分格式消除了寄生震荡，得到的波形更加理想圆滑，对时间步数区分更加细致，在选两波形点进行时间差计算式更加准确，从而得到故障点距离的精确度更高。根据Lax差分格式来分析电缆传输线方程，建立了电缆故障测距方法的模型，即低压脉冲法和脉冲电流法模型，可以很好地应用于电缆的开路，低阻故障，高阻故障的测距。仿真模型的建立，可以给检修人员提供更好的理论知识的培训，为以后的电缆故障检修提供了方便。行波法是建立在离线的基础之上的，随着技术的不断发展，在线监测会逐渐替代离线方法，但是目前行波法是最可靠的电缆故障测距方法。

参考文献：

[ 1 ] 李敏. 电力电缆故障测距分析研究[J]. 工程数学学报, 2015, 32(2):197-204.

[ 2 ] 陆金甫. 偏微分方程数值解法[M].北京:清华大学出版社,1987.

[ 3 ] 邱建贤, 尤克义. 一类广义的Lax-Friedrich格式[J]. 集美大学学报, 1998, 3(3):30-35.

[ 4 ] 郭裕顺. 传输线瞬态分析中基于电报方程—空间离散的有效方法[J]. 电子学报, 2001, 3(29):373-377.

[ 5 ] 黄俊彦,刘永强,马士超,等.基于Upwind差分格式的电缆故障测距仿真系统[J]. 光纤与电缆及其应用技术,2010,3(3):22-26.

[ 6 ] 窦磊, 王执铨. Lax-Wendroff差分法在高速互联线分析中的应用[J]. 信息与控制, 2005, 34(6):724-728.

[ 7 ] 郑生富. 传输线的一种时域有限差分法[J]. 重庆文理学院学报(自然科学版), 2007, 26(2):22-25.

[ 8 ] 张希, 刘宗行, 孙韬. 传输线的一种数值解[J]. 重庆大学学报(自然科学版), 2004, 27(2):116-119.

[ 9 ] 邱关源.电路[M].5版.北京:高等教育出版社, 2006.

[10] 刘勇刚. 基于时域分析的电缆线路故障测距[J]. 电气开关, 2009, 27(4):27-30.

[11] 高方平, 姚缨英. 含集总源均匀传输线暂态响应的时域求解[J]. 机电工程, 2012, 29(1):84-86.

[12] 张志斌. 故障电缆波形的时域分析及仿真研究[D]. 南宁:广西大学, 2008.