谐波检测方法的研究探讨
2017-04-03胡海棠陆文颖
胡海棠,陆文颖
(国网上海市电力公司检修公司,上海 200063)
0 引 言
随着科技不断地发展,创新,一些工业、民用或者商业上的负荷都是非线性负荷,是给电能质量带来谐波污染的主要来源。因此,电力系统的总谐波畸变率THD达到很高的值,就会使得电力网络的设备受损如烧损等。电力系统的谐波治理需要得到重视与改善[1]。
可以通过两种方式来抑制谐波:(1)搭建无源滤波器或有源滤波器,滤除谐波并补偿系统无功;(2)改善电力电子器件,减少谐波的产生。其中有源电力滤波的理论更先进,发展前景广阔,意义重大,是滤除谐波最高效简便的方式。
本文的主要工作是介绍了基于快速傅里叶变换的谐波检测方法,并且通过MATLAB软件的编程与Simulink电路搭建仿真进行谐波检测,得到检测结果。
1 基于快速傅里叶变换(FFT)谐波检测的原理
1.1 快速傅里叶变换概念
有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化为有限长的序列,但是DFT这种方法计算量太大,计算时间较长,在对电力系统谐波检测要求越来越高的前提下,该方法很难实时检测。因此,就引出了快速傅里叶变换,简称FFT,是 DFT 的快速算法,是 Cooley 和 Tukey在 20 世纪 60 年代在 DFT 的基础上提出的。快速傅里叶变换的出现,给信号处理带来了突飞猛进的发展,也给电力系统的谐波检测带来迅速的发展[2-3]。
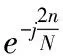
(1)
(2)
在所有的WN全都计算出的情况下,要经过N次复数乘法以及N-1次复数的加法才能计算一个X(k),那么如果要求出所有的N个X(k)就要进行次复数乘法以及N(N-1)次复数加法,计算量相当的大。因此需要 快速傅里叶 进行化简。首先要运用一些WN的一些性质。
WN的性质:
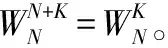
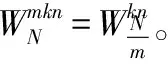
根据上面的性质再求级数X(k)时就可以将求和区间分为两部分:
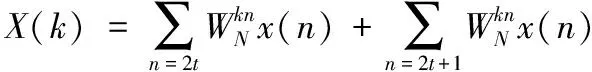
(3)
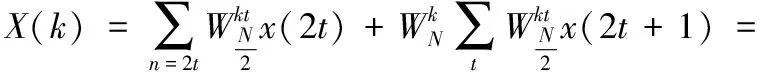
(4)
式(4)中:Fodd和Feven是两个分别关于序列奇数号序列和偶数号序列N/2点变换,由此只能计算出X(k)的前N/2个点,对后N/2个点由单位根的对称性,有:
(5)
(6)
这样,一个N点变换就分解成了两个N/2点变换。照这样可继续分解下去就可算出全部的X(k),且比DFT简单得多。
1.2 快速傅里叶变换谐波检测的实现
运用快速傅里叶进行电力系统谐波检测其主要原理是先进行谐波信号进行一个周期的采样,然后对采样得到的数据进行 快速傅里叶 处理,处理的结果就是谐波电流信号中所含有的频率成分以及它所对应的幅值和相位,这些信息可以很清楚的得到。因此运用快速傅里叶可以对频率信息进行辨识,能够较快的检测到信号中的各次谐波。但是该方法也有不足,在检测谐波时需要采集一个周期的信号才能分析出谐波成分,但是电网环境的变化是十分迅速的,系统中发电机、变压器、以及非线性负载的切除与投入都是在一瞬间完成,在这一个周期的时间内谐波的变化也是十分多样的,因此采样一个周期以后得到数据其实已经滞后一个周期了,无法达到实时检测的目的。为了对其进行优化,可以采用移动窗口法,具体原理是只要采样得到一个新的数据,就删掉最早的一个数据,让新加进来的数据和以前的数据构成一个数据窗,对其进行快速傅里叶处理,以提高检测的精确度[4]。快速傅里叶方法思路简单,原理十分清晰,可以根据需要对要补偿的谐波进行补偿,适用范围很广。
2 基于快速傅里叶的谐波检测
2.1 基于快速傅里叶谐波检测的编程设计
利用MATLAB搭建电路模型,运行程序后将其数据进行快速傅里叶函数分析,数据结果输出可得到电压与电流波形的谐波特性图,输出文件显示谐波的相关参数和计算结果THD%的值[5-9]。
1)程序运行后,显示两份数据图,某时刻t为该采样点时间,步长设置为1/50/N秒。第一份两个图分别为原始波形和抽取一个周波的信号波形,第二份两个图分别为快速傅里叶分析后的幅值-频率图、相位-频率图。
2)设置参数wq是为了保证避开过渡周期,抽取一个稳定的周波。该参数从第五个周波开始取N/4个点,即取一个周波。wq加上一个周波必须小于workspace的数据周期也就是10个周波,避免出现越线错误。
3)参数fp=30设置为倍频次数。为清晰显示,每周期采N点,fp设置为N/2,也可更改为≤N/2的值。
4)运行过程中,发现某次谐波相位变化很大,幅值很小,其实是快速傅里叶变换分析结果虚部实部都很小,误差大,在幅值极小时,相位为0。
2.2 六脉动整流电路及其滤波电容的快速傅里叶检测仿真
1) 电路设计
(1)六脉动整流电路电阻负载的搭建
如图1所示,首先利用MATLAB/simulink搭建电路模型

图1 六脉动整流电路电阻负载
(2)六脉动整流电路带滤波电容的搭建
如图2所示,在MATLAB/Simulink中搭建电路模型
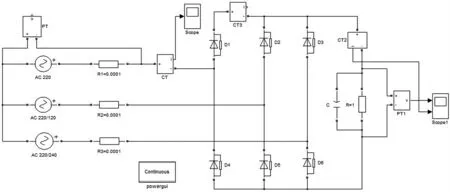
图2 六脉动整流带滤波电容电路
2)仿真结果分析
(1)六脉动整流电路电阻负载仿真结果
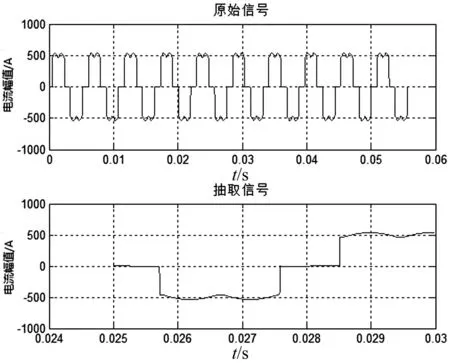
图3 六脉动整流电阻负载电流波形与取样波形
运行图1的电路后,运行程序,可得到交流侧电流波形图及其取样波形图如图3,快速傅里叶分析结果图4。观察输出的谐波分析结果,又由于六脉动整流电路主要含有的谐波次数为6k±1次,选择6k±1次谐波数据相比较可制成表1。
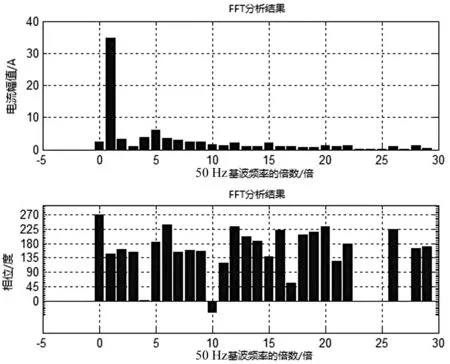
图4 快速傅里叶分析结果
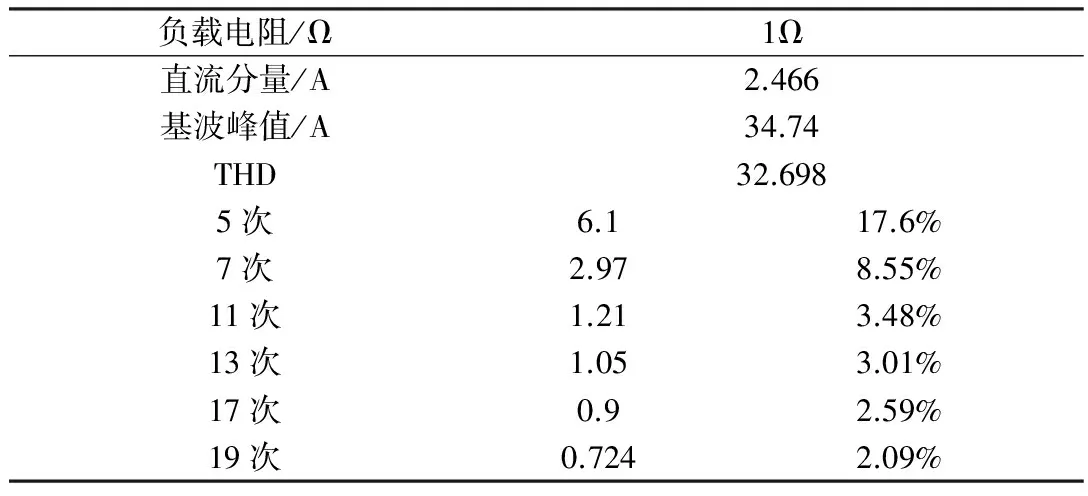
负载电阻/Ω1Ω直流分量/A2.466基波峰值/A34.74THD32.6985次6.117.6%7次2.978.55%11次1.213.48%13次1.053.01%17次0.92.59%19次0.7242.09%
对比数据表1可知,分析六脉动主要谐波有6k±1次,k取值越大,该次谐波含量越小。
(2)六脉动整流电路带滤波电容仿真结果
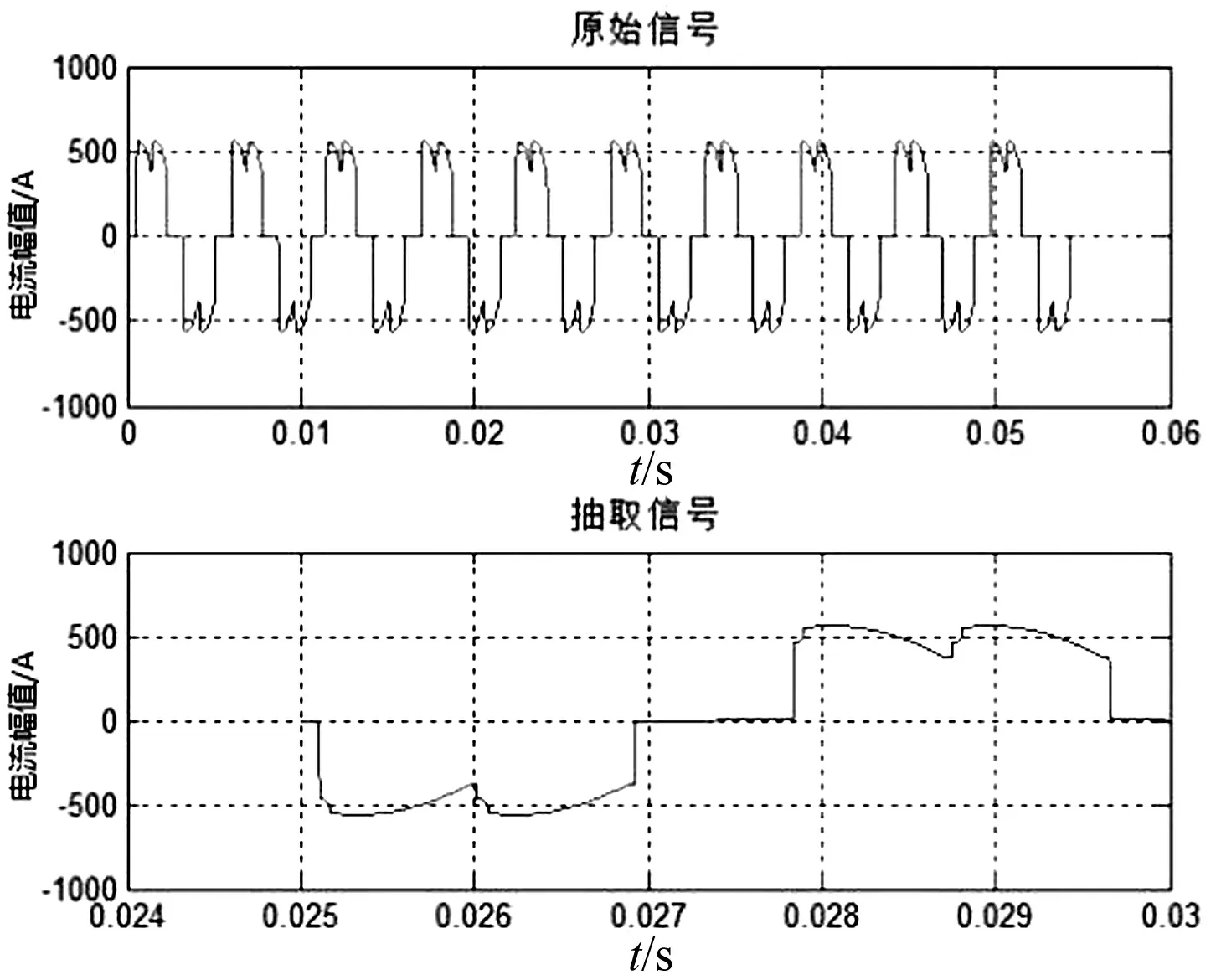
图5 六脉动整流带滤波电容电流波形与取样波形
运行图2的电路后,运行程序,可得到交流侧电流波形图及其取样波形图如图5,快速傅里叶分析结果图6。电阻值为1 Ω,电容初始值为1 000 μF,改变滤波电容值,观察输出的谐波分析结果,选择6k±1次谐波数据相比较可制成表2。
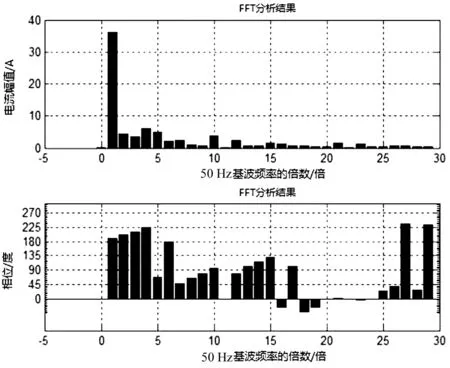
图6 快速傅里叶分析结果
可知电容越大,负载上的波动越小,但谐波越大。
(3)六脉动整流及其带滤波电容二者分析结果
滤波电容利用其两端电压不能突变的原理,二极管导通时充电,二极管截断时给负载放电,抑制电压,产生滤波波纹。根据电容放电的时间常数τ=RC,电容越大,滤波纹波越小。因此,仿真的结果符合理论。
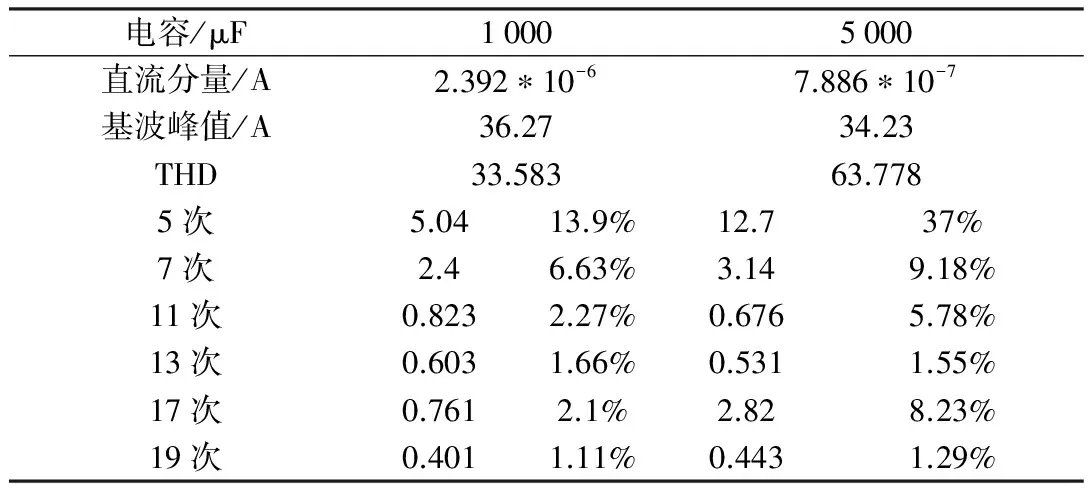
表2 改变电容值后谐波分析结果
3 结束语
本文以检测电路谐波为目的,学习了主要的谐波检测方法,选择快速傅里叶变换方法深入学习,用快速傅里叶方法检测电路谐波,并学习了滤波电容对不同含谐波电路及其谐波次数的抑制作用。通过MATLAB软件中Sinmulink模块和编程语句的设计进行电路谐波检测的仿真实验,最终将快速傅里叶理论来检测谐波的方法得到验证和深刻了解。本文的主要工作内容如下:
1)通过对谐波的研究,清楚认识到谐波对当今电网的危害,非线性负荷产生的谐波,会造成电网电压波形的畸变,让用电负荷受到严重影响,电能质量明显下降。因此,谐波检测十分重要,谐波的抑制对电能的质量起到关键作用。
2)对傅里叶理论及其谐波检测的应用进行深入学习,快速傅里叶方法检测谐波有大量研究理论与仿真实验,方法简单,原理清晰,在电网环境时刻变换的情况下,能够更精确、更快速地检测谐波。
3)运用MATLAB软件Sinmulink模块中powergui的快速傅里叶分析窗口验证快速傅里叶方法检测谐波的编程语句,powergui更为简单直观地输出检测结果,验证了程序设计的正确性。
4)以六脉动整流电路为实验对象,仿真得出其主要谐波次数不同,总谐波畸变量不同。
参考文献:
[1] 王兆安. 谐波抑制和无功功率补偿[M]. 北京:机械工业出版社, 2016.
[2] 杨丽娟, 张白桦, 叶旭桢. 快速傅里叶变换快速傅里叶及其应用[J]. 光电工程, 2004, 31(12):1-3.
[3] 黄峰, 杨洪耕. 基于快速傅里叶变换的谐波和间谐波检测修正算法[J]. 电网与清洁能源, 2010, 26(6):28-32.
[4] 陈晓光. 基于小波变换与傅立叶分析的谐波检测方法研究[D]. 哈尔滨:哈尔滨工业大学, 2009.
[5] 贺超英.MATLAB应用与实验教程[M].北京:电子工业出版社,2012.
[6] 马莉.MATLAB数学实验与建模[M].北京:清华大学出版社,2010.
[7] 李维波. MATLAB在电气工程中的应用[M]. 北京: 中国电力出版社, 2007.
[8] 张学敏.MATLAB基础及应用[M].北京:中国电力出版社,2009.
[9] 李欣媛,曾国宏.谐波及无功电流检测算法的MATLAB仿真[J].微计算机信息, 2010,27(13):159-160.
