基于核典型相关分析融合的XLPE电缆局部放电模式识别

妙旭娟，乔楷，冯玫，刘维

(1.国网新疆电力公司经济技术研究院，新疆 乌鲁木齐　830011，2.湖南科鑫电力设计有限公司，湖南 长沙　410000)

0　引　言

高压XLPE电缆绝缘缺陷的带电检测和在线监测是保障电缆正常运行的必要手段，其中脉冲电流法等局部放电检测方法被IEEE、CIGRE等国际电力权威机构一直推荐为最有效的电力设备绝缘状态评价方法。XLPE电缆不同绝缘缺陷模式、严重程度的快速准确识别是实现智能化电网的需要。

常用的局部放电模式识别方法可分为线性投影和非线性投影分析两种。如文献[1]使用主成分分析方法(PCA)方法对XLPE电缆局部放电信号统计特征进行分类就是典型的线性投影手段。部分研究基于核方法[2]、流形学习[3]和稀疏表示[4]等方法抽取局部放电样本的非线性特征。随着研究的不断开展，基于单一方式提取的局部放电信号特征难以满足识别精度的要求，使用多种手段进行有效融合得到组合特征，实现优势互补是当下研究的热点。

典型相关投影分析(CCA)是一种经典的多元数据统计分析方法，以两组及两组以上的特征集数据为主要内容，能够提取多组数据间的相关关系，而又尽量不丢失原始特征集的有效辨识信息，有效减少特征表示的冗余度。然而CCA无法提取不同特征之间的非线性关系[5]。在此基础上，Akaho于2001年提出将基于核技术的非线性降维方法引入CCA，提出了核典型相关分析(KCCA)[6]。现阶段，CCA和KCCA方法在气象信息预测、人脸识别、字符识别、图像处理等领域已有较多运用，但在电网信息和电力设备运行信息状态评估等领域应用极少。

本文提出将KCCA方法应用于XLPE电缆接头局部放电缺陷的模式识别，对运用多种手段获取的局部放电特征进行有效融合产生新的特征，既保留各特征的有效鉴别信息，又可以消除多特征的冗余信息。本文在高压XLPE电缆接头内部制作了4种典型绝缘缺陷，分别对各类缺陷电缆模型分别进行加压试验，使用高频电流检测系统采集得到局部放电信号，绘制PRPD图谱。对原始PRPD图谱以2维矩阵形式进行小波变换，采用KCCA方法对对原始PRPD图谱和变换后图谱两种特征进行融合，最后采用K近邻方法进行聚类分析。实验结果表明，使用KCCA融合方法比使用单一特征数据可以获得更高识别精度。

1　基于KCCA的局部放电特征提取

1.1　局部放电特征提取

PRPD图谱，即φ-q-n(相位-幅值-放电次数)三维图谱，是一种表征局部放电信息的常用统计方法，可以直观反映局部放电信号的相位分布特征。

对PRPD图谱进行向量表示，并进行正交小波变换后，选取低频分量作为新的特征量。分别对原始和小波变换后的PRPD图谱列向量使用随机映射或PCA等方法进行降维，一般情况下，特征维数较高，且两类特征间存在冗余信息。假设样本总数为N，分别用X=[x1,x2,…,xN]∈Rp×N和Y=[y1,y2,…,yN]∈Rq×N表示原始和小波变化后的PRPD图谱特征向量。CCA的关键是寻找一堆投影向量w和u，使得wTxi和uTyi具有最大相关系数，即如式(1)所示准则函数最大。

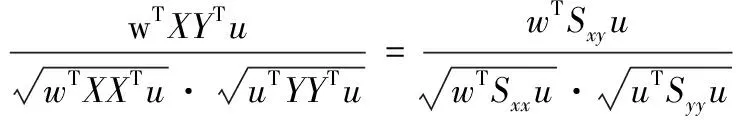
(1)

式中：Sxx∈Rp×p，Syy∈Rq×q分别表示特征集X和Y的自协方差矩阵，Sxy∈Rp×q表示X和Y的互协方差矩阵。

核方法是解决非线性模式分析问题的有效途径，其基本思想是将样本数据当前空间映射到更高维度的空间，即隐特征空间，使数据在隐特征空间中的映射是线性的，再运用线性方法降维。原始和小波变换PRPD图谱矩阵数据进行PCA所提取的特征向量。现在选择核函数φ和φ，分别将X和Y映射到高维特征空间，即φ:x→φ(x)，φ:y→φ(y)。则有φ(X)=[φ(x1),φ(x2),…φ(xN)]和φ(X)=[φ(y1),φ(y2),…φ(yN)]分别表示两组样本数据的高维核特征向量。w和u可以表示为如上特征空间的线性组合，即满足w=φ(X)α和u=φ(Y)β，则KCCA获得类似式(1)的准则函数如式(2)所示。

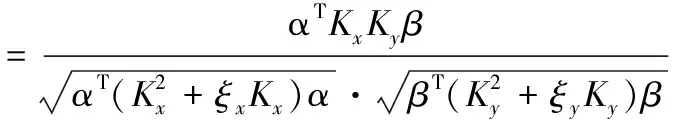
(2)

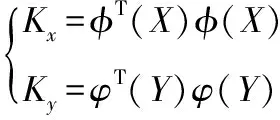
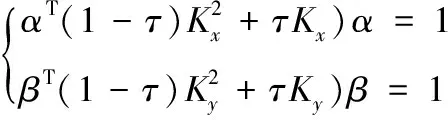
(3)

一般运用拉格朗日乘子求解上述带约束极值问题。几种常用的核函数如式(4)-式(7)所示：

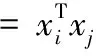
(4)

(5)

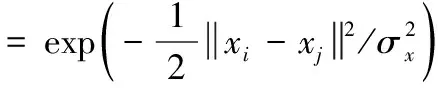
(6)

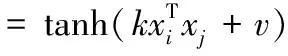
(7)

各种核函数在各种计算环境下的适用性不同，本文中选用式(6)，即高斯径向基函数，它能使非线性支持向量机具有良好的泛化性能。

求得α和β后，运行线性变换融合，最终经过KCCA后投影获取的组合特征向量为:

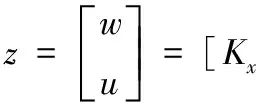
(8)

1.2　分类器构建

本文使用K最近邻算法(KNN)对所提取的局部放电特征向量数据进行模式识别，从而验证所提取的特征向量的有效性。KNN基本思想是给定一个待分类的样本z∈Rn，首先找到与zq最接近的或最相似的k个已知类别标签的训练集样本，据此确定zq类别。使用欧氏距离度量样本间的“近邻”，设由1.2章节确定的特征向量集Z中确定训练样本集Ztr假设zq,zq,…,zk为与zq距离最近的k个样本，共有s类样本，标签集合为C={e1,e2,…，es}，设目标函数f:Rn→ci，

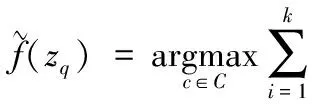
(9)

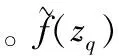
2　样本数据获取

2.1　缺陷模型设计

XLPE电缆局部放电缺陷主要由于不良的电缆或附件制作工艺、运行时的外力破坏或长时间的绝缘老化。电缆终端接头、中间接头等附件制作工艺复杂，需在安装现场进行手工制作，因此是绝缘缺陷多发位置。本文采用YJV-26/35 kV型电缆及其配套冷缩硅橡胶终端接头设计了4种典型绝缘缺陷模型，电缆接头结构及各缺陷模型示意图如图1所示。缺陷均在接头安装前制作，各缺陷及其制作过程分别为：(1)内部气隙放电：在电缆主绝缘表面纵向划痕，尺寸为10 mm(长)*2 mm(宽)*1 mm(深)，划痕周围避免涂抹高压硅脂；(2)悬浮电位放电：将尺寸为3 mm*3 mm的铜箔固定在主绝缘表面；(3)沿面放电：应力锥处半导电层断口位置残留2 mm×5 mm长半导电材料；(4)电晕放电：在主绝缘内置入一根3 mm长金属针并可靠碰触电缆铜芯。

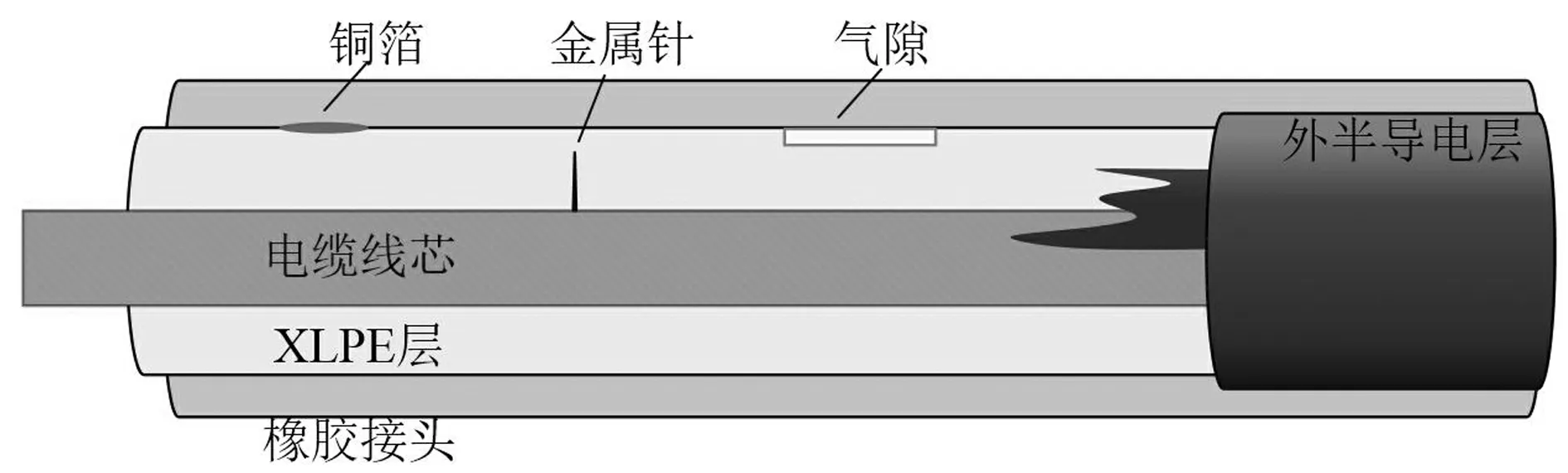
图1　高压电缆接头局部放电缺陷示意图

2.2　试验平台及检测系统

使用脉冲电流法检测系统局部放电。所用局放传感器为宽频罗氏线圈，工作频带为1 MHz-30 MHz。将传感器钳在电缆终端接头接地出现上，经前置放大电路与数字式示波器相连，模拟带宽为1 GHz，设置采样率为100 MS/s。每条样本数据为连续50个工频周期内的放电信号。每种缺陷模型各采集70条，共280条。信号采集时的各缺陷模型施加电压分别为18.5 kV，23.7 kV，20.5 kV，14.3 kV。

2.3　实验结果

利用实验采集的各组数据分别绘制PRPD图谱，各类缺陷放电的典型图谱如图2所示，各类缺陷放电的PRPD图谱表现出较明显差异性，但凭借主观判断对新加入的样本进行分类仍十分困难。

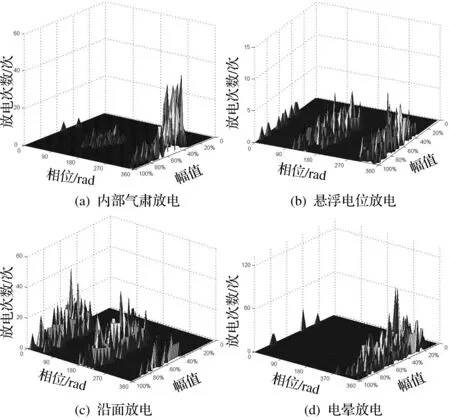
图2　各局部放电缺陷典型PRPD图谱

3　结果及分析

为验证本文方法性能，将本文方法应用于实验获得的PRPD图谱数据，每类缺陷放电各采集70条，共280条。每类样本随机选取40条用于训练，余下的作为测试样本。每个原始PRPD图谱为50*90维矩阵，使用KCCA进行压缩所获得的特征向量维数分别为10,20,40,60，各种情况下各进行10次实验并取平均值，所获得的识别精度如表1所示。

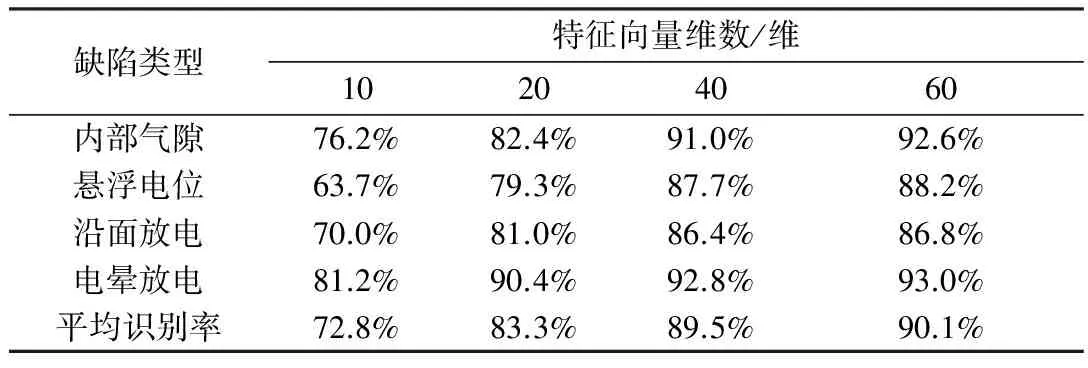
表1　基于本文方法识别正确率

观察表1中方法应用结果可知，基于KCCA方法提取的局部放电特征向量可有效表征信号内部特征信息，随着向量维数不断增加，识别正确率逐渐提高，且维数较小时增加较快，向量维数为40时，获得平均89.5%的识别正确率，足以满足实际应用需求。另外比较发现，各种缺陷放电的识别正确率存在一定差异，悬浮放电和沿面放电的识别效果明显低于另外两种，内部气隙放电的识别效果最好。分析可知，由于局部放电存在较大随机性，导致同一类型放电的PRPD图谱仍可能存在较大区别，直接影响了训练样本的有效性。另一方面，悬浮放电和沿面放电PRPD图谱存在某些相似特征，易造成错分。当然，样本数量，KCCA方法参数选择均会对识别效果产生不同程度的影响，在后续研究中将做着重分许。

4　结束语

本文基于核典型相关分析方法提取局部放电信号PRPD图谱的特征信息，可以有效反映信号内部的非线性特征并减少信息冗余度，使用K最近邻分类方法，可以失效不同局部放电模式的识别。使用XLPE电缆及接头设计了4种典型绝缘缺陷模型，使用脉冲电流法采集获得足够局部放电信号样本，在不同特征向量下验证了本文方法有效性，获得了90%以上识别正确率。

参考文献：

[1] 苑津莎,尚海昆. 基于主成分分析和概率神经网络的变压器局部放电模式识别[J]. 电力自动化设备,2013,41(6):27-31.

[2] 律方成,金虎,王子建,等. 基于组合核多特征融合的GIS局部放电检测与识别[J]. 电工技术学报,2014,39(10):334-340.

[3] 律方成,张波. 基于LLE降维和BP_Adaboost分类器的GIS局部放电模式识别[J]. 电测与仪表,2014,51(15):37-41.

[4] 姚林朋,王辉,钱勇,等. 基于半监督学习的XLPE电缆局部放电模式识别研究[J]. 电力系统保护与控制,2011,39(14):40-46.

[5] 王大伟,陈浩,王延杰. 核典型相关分析的融合人脸识别算法[J]. 激光与红外,2009,39(11):1241-1245.

[6] 郗仙田. 正交正则化核典型相关分析的研究[D].吉林：东北电力大学，2016.