基于振荡相位差的低频振荡扰动源定位方法
2017-04-03张文朝商显俊李轶群潘艳贾琳高洵
张文朝, 商显俊, 李轶群, 潘艳, 贾琳, 高洵
(1.中电普瑞电力工程有限公司,北京 100000; 2.国网江苏省电力公司 常州供电公司,江苏 常州 213000;3.国家电网公司 华北分部,北京 100000)
0 引 言
随着电网互联规模的不断扩大,低频振荡已经成为威胁电网安全稳定运行的重要问题。在已经发生的低频振荡事故中,既有由于系统阻尼不足引起的弱阻尼甚至负阻尼自由振荡,也有因持续的周期性小扰动引起的强迫功率振荡[1-2]。低频振荡的实质是发电机转子之间的相对运动,各转子的振荡频率和转子间的振荡相位差较为固定。受转子相对振荡的影响,线路功率和母线电压、频率也将出现不同程度的同频振荡[3-5]。在扰动源没有切除的情况下,振荡将持续存在,并有可能扩散而导致系统失稳[6-7]。
发生低频振荡后,首要问题是快速准确地定位扰动源。基于广域测量系统(wide area measurement system, WAMS)的实测数据进行扰动源在线识别是低频振荡监测与控制的研究热点。文献[8-10]证明了发电机能量消耗和其阻尼转矩的一致性,并且提出了一种计算能量流的实用方法,减少了暂态能量分量,根据能量的消耗或产生判断振荡源。文献[11-12]基于关键线路的WAMS动态信息构建不同层次的网络割集,将振荡能量流出的割集判断为振荡源,并通过力矩分解的方法,将扰动源精确定位至发电机的控制系统。文献[13]采用经验模态时空滤波功能,提取所需电气量的主导分量,基于经验模态能量趋势函数自动识别扰动源。目前,电力系统内相量测量单元(phasor measurement unit, PMU)的配置尚不完整,无法获取整个网络的电气量信息,研究基于局部信息的扰动源定位方法意义重大。
振荡是一种在自然界广泛存在的物理现象,其实质是一种能量传播的形式。在物理振荡中,沿着振荡波的传播方向,各质元的振荡存在一定的相位差,靠近波源的质元在相位上超前远离波源的质元。电力系统的低频振荡同样是一种物理振荡,扰动源机组相当于波源,它是主动振荡的;非扰动源机组相当于波源周围的质元,它们受扰动源影响而被动地振荡。本文分析了在低频振荡过程中,电力网络各点的振荡相位分布关系,提出了一种基于振荡相位差的低频振荡扰动源定位方法。利用希尔伯特-黄变换(Hilbert-Huang transform, HHT)处理振荡数据,准确计算各点的瞬时振荡相位。本方法仅凭一种电气量即可实现扰动源定位,较已有方法更为简单直观。通过对华中电网的仿真分析,验证了本文方法的有效性。
1 扰动源定位方法
1.1 扰动机理概述
在一个电力网络中,任一发电机发出的功率是该发电机电动势相对于其他发电机电动势相量的相角差的函数,即:
(1)
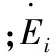
由式(1)可知,扰动源机组转子主动的振荡会影响受扰机组的电磁功率,导致受扰机组转子的转矩不平衡而被迫振荡。当扰动源机组的电动势角度增大时,受扰机组的电磁功率将减小,其机械转矩将大于电磁转矩,从而受扰机组的电动势角度也开始增大,并趋向于保持两机的转子角度差与初始值一致。在振荡过程中,受扰机组的转子角度始终在追赶扰动源机组的转子角度,并且由于其转子惯性的存在,其振荡相位滞后扰动源机组。
由于式(1)中包含了节点之间的互导纳,因此某台发电机的电磁功率主要受其附近机组的电动势相角影响。在振荡过程中,扰动源主要影响的是其近端的机组,近端机组受扰后再进一步影响远方的机组,沿着振荡能量的传播方向,机组转子的振荡相位依次滞后。在其他条件相同的情况下,机组间的电气距离越小,相互间的同步力越大,则振荡相位差越小。
1.2 扰动源定位判据
综上所述,可使用以下判据进行扰动源定位:
1)电厂就地信息判据:扰动源机组转子角度(频率)振荡的相位应超前其升压变高压侧电压角度(频率)的振荡相位;非扰动源机组转子角度(频率)的振荡相位应滞后其升压变高压侧电压角度(频率)的振荡相位;
2)网络信息判据:对于一条连接扰动源近区和外部网络的输电线路,靠近扰动源一端母线的电压角度(频率)的振荡相位将超前远离扰动源一端母线电压角度(频率)的振荡相位。
振荡相位差是一个带方向的量,根据第1条判据,仅需获取电厂就地的电气量信息即可识别扰动源,在网络和其余电厂信息缺失的情况下,仍然能够准确定位具体的扰动源机组;在部分网络信息能够获取的情况下,根据第2条判据可以判断振荡能量的来源,收缩扰动源的可疑区域。
在低频振荡过程中,网络结构突变等因素可能导致振荡相位短时发生混乱,而且从PMU采集的数据往往包含了较多的干扰信号。以上因素可能在较短时间内影响振荡相位的计算结果,因此仅仅比较个别时刻的振荡相位难以保证结果的准确性。为准确描述在一段时间内两点振荡的总体相位关系,定义振荡相位差:

(2)
对于电厂就地信息判据来说,式(2)中的θ1和θ2分别是转子角度(频率)和升压变高压侧的电压角度(频率)振荡相位;对于网络信息判据来说,式(2)中的θ1和θ2是两侧母线的电压角度(频率)振荡相位;t1和t2分别为计算的起始时刻和终止时刻。
2 振荡相位差计算
2.1 希尔伯特-黄变换
电力系统是一个非线性的动态系统,振荡数据中可能包含多个振荡模式,这种复合信号的相位是没有物理意义的。而且在振荡过程中,全网的稳态频率往往偏离额定频率,电压角度和频率的振荡曲线将相对水平轴发生偏移,难以直接计算相位。因此,需对振荡数据进行模式识别与分解,提取出主要振荡模式后再进行相位计算。
HHT包括两部分,第一部分是经验模态分解(empirical mode decomposition, EMD),第二部分是希尔伯变换(Hilbert transform, HT)。EMD是一种自适应信号时频处理方法,它能将复杂信号分解为有限个固有模态函数(intrinsic mode function, IMF)分量和剩余分量,即:
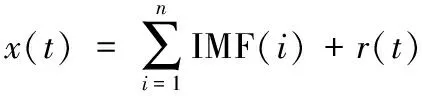
(3)
式中:x(t)为原信号;r(t)为剩余分量;IMF(i)为第i个固有模态函数。
各IMF分量必须满足以下2个条件:(1)整个数据段内,极值点的个数和零点的个数必须相等或至多差1;(2)在任何时间点上,由局部极大值点形成的包络线和由局部极小值点形成的包络线的平均值为0。各IMF分量的瞬时相位具有明确的物理意义,取其主导分量进行希尔伯特变换。
一个实连续信号u(t)经希尔伯特变换后将得到一个与其正交的共轭信号v(t),其变换表达式为:
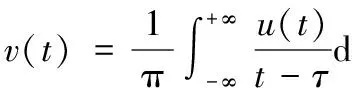
(4)
原信号与变换后的信号可以构成一个复信号:
q(t)=u(t)+iv(t)
(5)
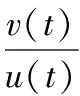
2.2 计算起始时刻
在起振阶段,电网刚刚受到扰动,振荡尚未平稳,相位可能较为混乱,因此希尔伯特-黄变换的计算起始时间宜取为扰动发生1~2个周期之后。由于信号周期性振荡,希尔伯特变换得出的振荡相位在-π~π内循环变化,在相位达到π后,将瞬间重置为-π。在相位重置后的一小段时间内,原本领先的信号在相位数值上将小于落后的信号。因此,振荡相位差的计算起始时间选取不当可能会得到相反的计算结果。
本方法对电气距离较近的节点进行相位差计算,因此相位曲线的位置差别不会太大。取其中一个信号的重置点为观察点,如果在其左侧附近另一信号发生重置,则就以该观察点作为计算起始点;如果在其右侧附近另一信号发生重置,则以另一信号的重置点为计算起始点。为了能计算多个振荡周期的总体相位差,瞬时相位采取不循环的数值,即在第n次回到-π后,此后一个周期内的数据均加上2nπ。
3 算例分析
以华中电网为例,验证本方法对负阻尼振荡的适用性。通过更改锦一电厂机组的控制系统参数和出线电抗以弱化厂内机组阻尼。设置锦一电厂1回出线无故障跳闸,激发负阻尼振荡。华中电网部分500 kV网架结构如图1所示。
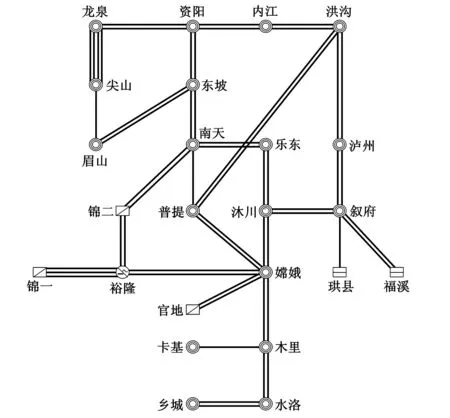
图1 华中电网地理结线图
利用电厂就地信息进行扰动源机组的排查,锦一电厂1#机组转子及其升压变高压侧的标幺化电压角度如图2所示。
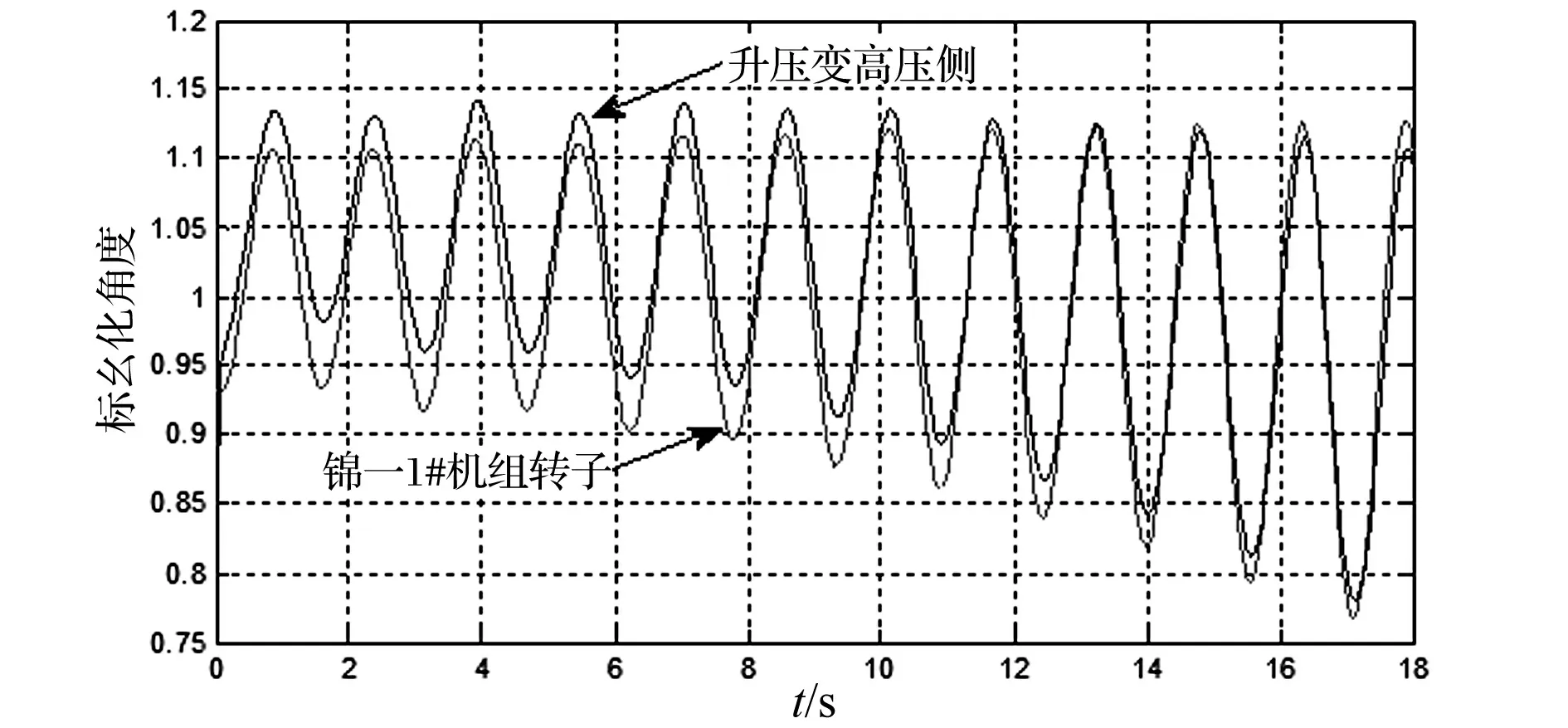
图2 标幺化角度波动图
官地电厂1#机组转子和升压变高压侧的标幺化电压角度如图3所示。

图3 标幺化角度波动图
仔细观察图2、3可见,锦一电厂1#机组的转子角度到达最大值或最小值的时间早于升压变高压侧电压角度;而官地电厂1#机组的转子角度到达最大值或最小值的时间晚于升压变高压侧电压角度。用希尔伯特-黄变换计算其主导振荡模式的振荡相位,计算起始时间为扰动发生后2 s(2 s作为新的时间0点),结果如图4、5所示。

图4 振荡相位图

图5 振荡相位图
锦一1#机组转子和机端的振荡相位差较小,但局部放大后能明显看出转子角度的振荡相位领先于高压侧电压角度;而官地1#机组转子角度的振荡相位明显滞后于高压侧电压角度。计算两台机组在仿真时间内的振荡相位差,锦一1#机组的计算起始点为1.23 s,官地1#机组的计算起始点为1.56 s,结果如图6所示。根据扰动源定位判据,扰动源机组为锦一电厂机组。
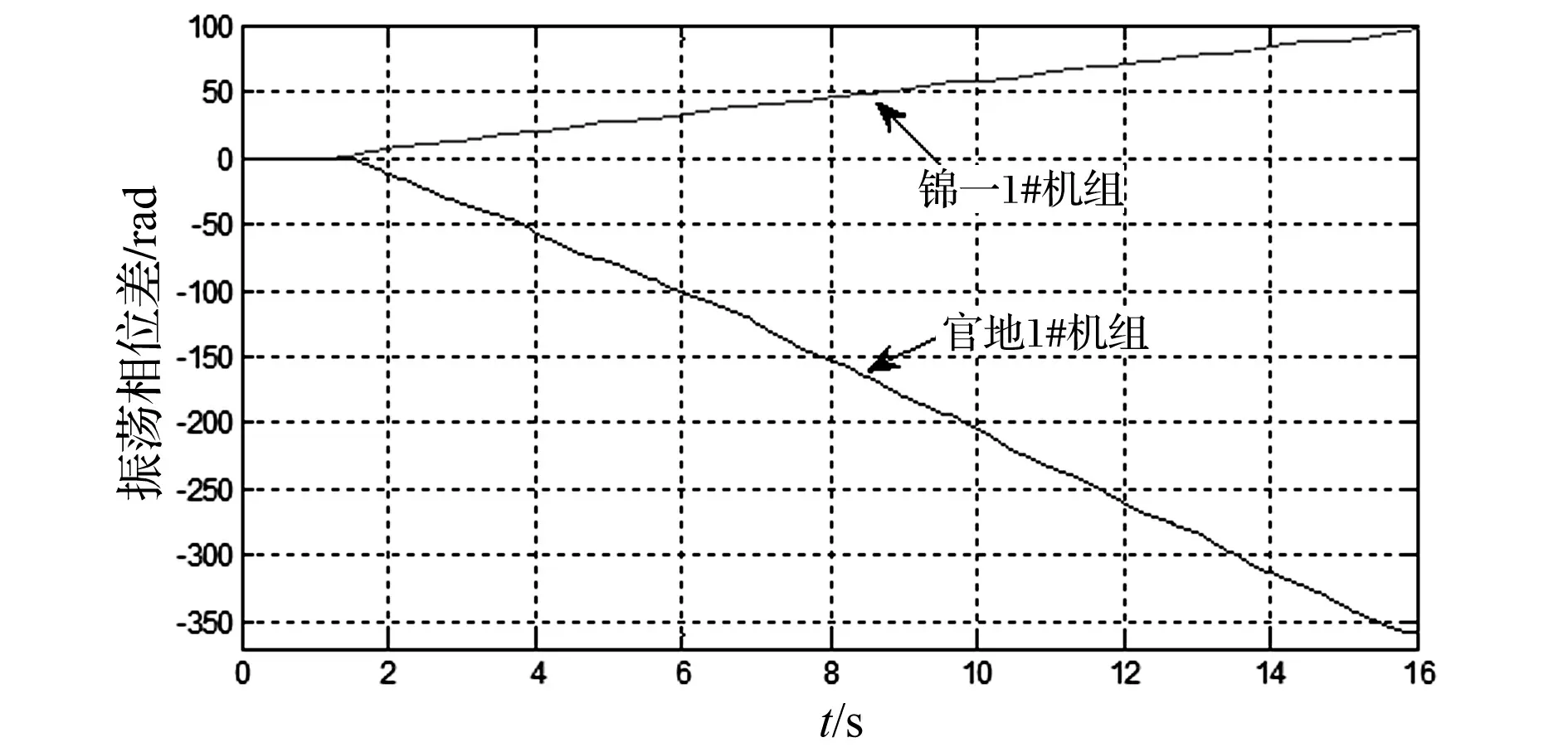
图6 振荡相位差
在能够获取部分网络信息的情况下,可以进行扰动源方位的判定。对川渝断面、嫦娥—沐川和锦二—南天4条输电线路的振荡相位差进行计算,计算结果如表1所示。

表1 网络振荡相位差计算结果
可见,对比输电线路两端母线电压角度的振荡相位,远离扰动源的一端要滞后靠近扰动源的一端,根据网络信息能够明确判定扰动源的位置。
4 结束语
本文提出了一种基于振荡相位差的低频振荡扰动源定位方法。分析了扰动源机组影响系统内其他机组的机理,并基于两机振荡简化模型,证明了从扰动源机组到被扰动机组,各点的电压角度和频率振荡相位逐渐滞后的相位分布特点。借助希尔伯特-黄变换准确计算主导振荡模式的瞬时相位,根据电厂就地的电气量相位关系即可定位扰动源机组。为避免突然扰动和数据质量对振荡相位的短时扰乱,通过计算振荡相位差量化电气量整体的振荡相位关系。华中电网仿真计算结果表明,本方法准确性良好,具有工程应用价值。
参考文献:
[ 1 ] 杨东俊,丁坚勇,邵汉桥,等.基于WAMS的负阻尼低频振荡与强迫功率振荡的特征判别[J].电力系统自动化,2013,37(13):57-62.
[ 2 ] 汤涌.电力系统强迫功率振荡的基础理论[J].电网技术,2006,30(10):29-33.
[ 3 ] 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002.
[ 4 ] 王铁强,贺仁睦,王卫国,等.电力系统低频振荡机理的研究[J].中国电机工程学报,2002,22(2): 21-25.
[ 5 ] JING C,MACALLEY J D,KOMMAREDD Y M.An energy approach to analysis of interarea oscillations in power systems[J].IEEE Trans on Power Systems,1996,11(2):734-740.
[ 6 ] 李莹,贾文双,李文锋,等.基于起振段波形在线判别电力系统功率振荡性质[J].中国电机工程学报,2013,33(25): 54-60.
[ 7 ] 杨海涛,丁茂生,宋新立.电力系统动态稳定机理和稳定措施分析[J].电力系统自动化,2008,7(25):35-39.
[ 8 ] 陈磊,闵勇,胡伟.基于振荡能量的低频振荡分析与振荡源定位(一)理论基础与能量流计算[J].电力系统自动化,2012,36(3):22-27.
[ 9 ] 陈磊,陈亦平,闵勇.基于振荡能量的低频振荡分析与振荡源定位(二)振荡源定位方法与算例[J].电力系统自动化,2012,36(4):1-5.
[10] LEI CHEN,YONG MIN,WEI HU.An energy-based method for location of power system oscillation source[J].IEEE Transactions on Power Systems,2012,28(2):828-836.
[11] 李文锋,郭剑波,李莹,等.基于WAMS的电力系统功率振荡分析与振荡源定位(1)割集能量法[J].中国电机工程学报,2013,33(25):41-46.
[12] 李文锋,李莹,周孝信,等.基于WAMS的电力系统功率振荡分析与振荡源定位(2)力矩分解法[J].中国电机工程学报,2013,33(25):47-53.
[13] 褚晓杰,印永华,高磊,等.基于经验模态理论的强迫振荡扰动源定位方法[J].中国电机工程学报,2014,34(28):4906-4912.
