夯实基础 拓展提升
——《百分数解决问题》教学实践与思考
2017-04-02徐晓良徐丹红
徐晓良 徐丹红
【教学内容】
人教版六年级上册第90页。
【教学过程】
一、谈话引入,直接揭题
师:今天我们一起学习用百分数解决问题,在前面的学习中你对百分数已经有了哪些了解呢?
生:我们学习了百分数的认识,百分数的含义。
生:我们还学习了百分数的计算。
师:同学们对于百分数已经掌握了很多知识。那你在生活中哪里见过百分数呢?
生:在抽奖活动中见过。
生:下载软件的时候见过。
生:食品成份中会写鸡蛋占了百分之几。
【说明:引导学生用数学的眼光去看待生活、寻找生活中的百分数能更好地理解百分数,也为后面问题的提出做了很好的铺垫。】
二、问题解决,学习假设
师:徐老师前几天看到了一则和百分数有关的小广告,今天和大家一起分享一下。
师:看了这则促销的消息,你有什么想说的吗?
XX车行活动信息
十一月信息:由于进价提高,自11月1日起,自行车价格上涨20%;
十二月信息:为了回馈消费者,自12月1日起,自行车价格下降20%,恢复到10月份的价格。
生:12月1日去买比较好。
师:你是认为12月的价格比较——
生:便宜!
生:我认为他这则信息有错误。
师:那你能告诉大家哪句话出错了吗?
生:我认为不能恢复到10月份的价格,会和10月份的价格有一些变化。
师:同学们能用数学的眼光分析生活中的问题并能提出质疑,非常棒!那么最后的价格是真的恢复到了10月份的价格,还是像我们同学所说的和10月份相比会有些变化呢?如果交给你,你能解决吗?请把你的想法写下来。
【说明:教师没有直接提出问题,而是让学生自己分析发现问题,并提升学生的问题作为课堂研究的主问题,不仅能让学生带着思考解读信息,而且激发了学生提出问题、解决问题的热情。】
(学生独立完成,教师巡视)
师:谁愿意和大家交流一下你的想法?
生:假设10月份的价格是100元,那么11月份是100+20%=120(元),12月份是120-20%=96(元)。
(板书算式)
师:有没有同学对他的算式有不同意见?
生:我完全看不懂算式中的20%是谁的20%,不知道他是怎么做的。
师:你的意思是他的算式中没有表示出是谁的20%,是吗?那么谁来帮助他把算式补充一下?
生 :100 ×(1+20% )=120(元)。
师:现在你能看出是谁的20%了吗?
生:是10月份的20%。
师:其实这位同学用100+20%是想表示100+100×20%,而这个算式又可以表示成100×(1+20%),这样计算的结果就是哪个月的价格?
生:11月。
师:11月知道了,我又应该如何求12月呢?
生:12月价格比11月下降了11月份的20%。
生:120×(1-20%)=96(元)。
师:如果老师用下面这条线段表示10月的100元,那么11月份应该怎么表示?
生:再加上20%。
师:这个20%该怎么表示?
生:把10月平均分成10份,取其中的2份线段。
生:也可以直接平均分成5份,取其中的1份。
师:那么12月应该是在——
生:把11月平均分成5份,少了其中的1份。
师:同样是20%,在图上为什么表示不一样呢?

生:因为它们的单位“1”不同。
【说明:借助线段图,为学生提供了思考的直观工具,厘清了三者之间的关系。同时,也利用线段图的直观冲击让学生进一步理解两个20%在表示实际量上的不同及其不同的原因。】
师:单位“1”发生了变化,所以最后结果也发生了变化。那么假设100元,得到了下降的结论,如果假设的是其他的数呢?
生:还是一样的。
师:有同学假设不同的数吗?和大家来交流一下。
生:我假设的是10元,10×(1+20%)=12(元),12×(1-20%)=9.6(元)。
生:我假设的是 1,1×(1+20%)=1.2,1.2×(1-20%)=0.96。
师:为什么我们假设的数是不同的,得到的结论却都是下降呢?
生:11月份上涨的20%是以 10月份为单位“1”,而 12月份是以上涨了的11月份的价格为单位“1”,所以12月份的价格比10月份的价格要低。
生:下降的是上涨后的20%。
师:意思是说下降得要多,上涨的要少。
师:同学们刚刚是用分步计算得出结果的,有的时候综合计算会给我们一个新的观察角度。你能把上面的算式合并成综合算式吗?
学生说综合算式,教师板书如下:
100×(1+20%)×(1-20%)=96(元)
10×(1+20%)×(1-20%)=9.6(元)
1×(1+20%)×(1-20%)=0.96
师:观察这些综合算式,你又有什么新的发现?
生:都是乘(1+20%)×(1-20%)。
生:不管假设多少,12月和10月的价格关系不变,都是求单位“1”的百分之几是多少。
师:在这里是求单位“1”的百分之几呢?
生:是求单位“1”的96%。
师:96%是怎么来的?
生:120%×80%=96%。
100×(1+20%)×(1-20%)=96(元)
120%×80%
96%(0.96)
师:都是求单位“1”的96%是多少,那我把单位“1”假设成a可以吗?
生:可以!
师:那么就是求a的——
生:96%是多少。
师:a乘以96%,乘以一个比1小的数,结果——
生:比a小。
师:当然这里的a能不能为0啊?
生:不能。
师:结果是?
生:0.96a。
教师将线段图中的100元改成a,12月份改成0.96a。
师:而且我们从图上很明显的看到,最后结果下降了,你知道下降了百分之几吗?
生:4%。
师:这个4%就是下降的幅度。这个下降的幅度和前面假设是多少有关系吗?
生:没有!
【说明:解决问题的过程放手让学生独立完成,给不同解决问题的方法、不同假设数据的呈现提供了可能。而后又巧妙的利用综合算式,将这些不同的情况进行对比,让学生由模糊变得清晰:这类解决问题无论多么复杂最后都可以化繁为简为“求一个数的几分之几是多少。”】
三、变式练习,渗透模型
师:刚刚我们发现自行车的价格先经过了上涨,又下降,最后结果是下降了4%。如果是先下降后上涨呢?
(边说边出示折线统计图)
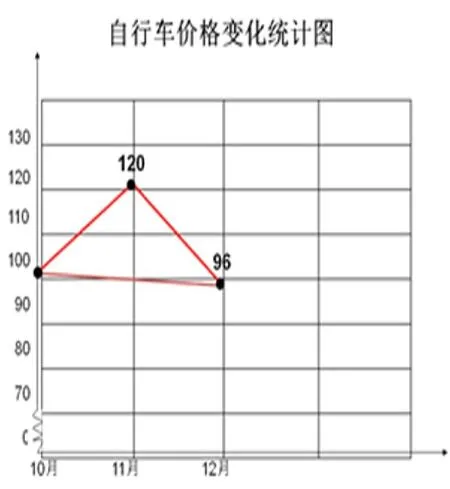
生:(犹豫着说)变大了。
生:可能还是下降的。
师:请你算一算是涨了还是降了,如果可以直接列综合算式就列出综合算式。
生:怎么还是下降了?
师:还是下降?谁来说说你是怎么计算的。
生:假设是 a,a×(1-20%)×(1+20%)=0.96a。
师:明明现在变成了先降后涨,怎么结果还和先涨后降是一样的呀?
生:先降的话,后面涨的就少了。
生:在下降的基础上涨。
师:刚刚在同学的回答过程中,老师感觉到你们的脑海中都有了一幅新的线段图。你们发现了什么?
(出示前后两幅线段图)
生:下降的20%还是比上涨的20%多。
师:还是因为——
生:单位“1”发生了变化。
师:下降幅度是——
生:4%。
生:我有补充,不管是先降后涨还是先涨后降,都是计算一个数的96%。
生:其实就是乘法交换律,(1-20%)和(1+20%)交换了一下而已。
师:所以表面上看,变化过程是不一样的,但变化的结果和变化的幅度是一样的。先下降20%,后上涨20%,最后是下降了。那如果还是先下降20%,后上涨30%呢?
生:肯定是涨了,涨了4元。
师:非常厉害,还能一下子知道涨了多少。算式表示出来可以吗?谁来和大家分享一下你的算式?
生:假设十月份售价100元,100×(1-20%)×(1+30%)=104元。
师:涨了多少呀?
生:4元,是100元的4%。
师:刚刚咱们下降20%,上涨20%,结论是降了;下降20%,上涨30%,是涨了。如果店家想恢复到10月份的价格,那上涨百分之多少能恢复到原价呢?
【说明:用折线统计图来展示变化的幅度是一个亮点。通过折线的变化这种形象的描述,让学生对于变化幅度有了一个直观的认识,课堂效果很不错。】
生:应该是25%。
生:肯定是在20%和30%之间。
师:你能通过计算算出来吗?试一试!
生:上涨25%,我是想0.8乘以几等于1。
师:你们听明白他的意思了吗?
生:就说假设原价是1元,下降后是0.8元,那么0.8乘以多少才能仍旧等于1。
师:也就是说单位“1”只有乘以1才能仍旧等于单位“1”,而前面是0.8,0.8乘以1.25正好等于1。
板书:
1×(1-20%)×(1+?)=1
0.8×?
1
师:看来我们的猜测还是非常准的。还有不同的想法吗?
生:下降后是80元,涨回到100元,要涨20元,20元是80元的25%。
生:(100-80)÷80=0.25=25%。
师:求100比80多了百分之几,可以从不同的角度来解答恢复到原价需要上涨百分之几。我们通过计算发现,如果上涨幅度和下降幅度是一样的话,绝对不会——
生:和原价相等。
师:下降20%,要上涨25%才能回到原价,这是为什么呢?
生:因为单位“1”不同。
师:看来在百分数解决问题中单位“1”的变化对最后的解题起着很大的作用,所以我们要找清单位“1”。
【说明:通过先涨后降和先降后涨两种情况的对比,使学生进一步熟练假设法的使用,也进一步理解了这类题型的意义。而通过“涨百分之多少能回到原价?”问题的解决则更进一步理解单位“1”对于百分数的意义。同时,也通过两者的结果相同,让学生体会到了变中有不变的思想。】
