充分体现数学学科的逻辑性与严谨性——“一个数除以分数”的教材编排分析和创新性教学设计

张宏伟（特级教师）

“一个数除以分数”的计算法则是小学计算法则推导中的一个难点。这部分内容到底该如何编排和教学才更为科学、更为严谨、更为简洁，更便于学生自己研究、理解和掌握呢？笔者对现行几种版本的编排进行了对比研究和分析，并找到了一种全新的设计方案，经过教学验证，效果非常好。现把笔者的一些想法和做法写下来与大家分享和交流，不当之处还请各版本教材编者和教师指正。

一、各版本教材编排的对比和分析

现行教材的编排综合起来大致有四类不同的编排思路：

第一类是借助解决实际问题，用“实证”的方法进行推导。代表的版本有北京版教材（六年级上册第 18、19页）、人教版教材（六年级上册第31页、32页）等。下面以北京版教材例题3为例进行分析。

该类教材编排的推导过程分为五步：第一步，基于学过的数量关系类推出解决问题的除法算式；第二步，通过画图分析把除法应用题转换成用连乘法解决的问题；第三步，基于除法算式和连乘算式都是解决同一个问题，建立除法算式和连乘算式的相等关系；第四步，利用乘法结合律把后面两个数相乘，得到除数的倒数，实现“除以一个分数等于乘以这个分数的倒数”的转化；第五步，学生依据举的例子类推和验证，进行不完全归纳，“发现”和总结计算规律（法则）。

笔者认为这种类推有三点局限：一是特别的“绕”，很多学生在接近10次的列式、画图、分析的迂回中被绕迷糊了，以至于很多学生理解起来倍感困难。二是第三步“强硬地”使用乘法分配律把后面两个数先相乘，不是学生内心的需要、不是计算必需的，是为了证明而不得已刻意为之，学生并不能从心底比较“舒服”“自然”地认同，更不是学生自己的生成，是被强迫地顺应。三是没有从数学内部逻辑地进行数理推理和证明，不符合数学“简洁”的追求，无论是教师、还是学生总有一种不完美、不完善、不透彻的感觉。

第二类是借助“实证式的具体、形象、真实的图形”和类推进行证明。代表版本是北师大版教材（六年级上册第57、58页）和苏教版教材（六年级上册第56、57页）。

该类教材编排先是让学生借助分析实际问题中的“具体、形象、真实的图形（饼、长方形和条形图）”“看到”除以几分之一，就等于乘以几（即几分之一的倒数），然后再直接类推到“除以几分之几，也等于乘以这个分数的倒数”。

这种编排也有两点局限：一是除以几分之一，还是实例验证性的研究，没有从数学内部的逻辑推理和证明“为什么除以几分之一等于乘以几”。二是类推到除以几分之几，是强行的类推，没有编排验证这种类推是否正确的环节，而数学的类推本身也是需要证明的，因为有的类推是成立的，有的类推也可能不成立。这对于数学的严谨性而言，是有疏漏、缺憾的。可以这样补救：比如，编排可以化成小数计算的分数除法验证，或者化成同分母分数，以包含分数单位的个数相除的方式证明这种类推是正确的（见下面浙教版例题1）。

第三类以青岛版教材（六年级上册第 23、24页）为代表。

这种教材编排和第一类（北京版）编排类似，也是从解决实际问题入手，“从生活到数学的推导路径”——共分三个模块进行。第一个模块先解决整数除以几分之一，通过对问题的分析和转换，找到实际解决这个除式的乘法算式（整数乘以分数的倒数），让学生发现整数除以几分之一等于这个整数乘以几（即这个分数的倒数）。第二个模块解决整数除以几分之几，通过对实际问题分析和转换，找到解决这个问题的另一个算式 a×b÷c，再 b÷c 转化。第三个模块让学生自己借助统一问题，仿照模块二分析，导出一个数除以一个分数的算法。

这种编排存在的问题和第一类基本相同（模块二对b÷c的处理手法和第一类编排的第三步如出一辙），而且整个分析和转化的过程更加生涩、难懂。

第四类，以浙教版教材（五年级下册第56、57页）为代表。

该教材编排从两条不同的路径进行了证明：

第一条路径是结合解决问题，引导学生把分数除法先转化为同分母分数除法，再转化成“包含分数单位的个数”相除（即分子相除）；最后再和第二个因数是除数的倒数的乘法算式比较计算结果，让学生发现“除以一个分数”和“乘以这个分数的倒数”计算结果总是一样的，得出“除以一个分数等于乘以这个分数的倒数”的结论。

第二条路径是利用“商不变的性质”，将被除数和除数同时乘以除数的倒数，将除数转化为1来推导。

笔者感觉这类教材的编排更有新意、更简洁，也比较容易理解。但是也有两点值得商榷：一是第一条路径还是直接对比除的结果、和乘以倒数的结果，硬性地给予，不是学生自己能想到的（大多数不会想到和乘以这个分数的倒数的乘法算式对比）。二是第二条路径是把整数商不变的规律直接强硬地类推到分数除法，没有证明这种类推是成立的（数学的类推本身也需要证明）。三是这种“空降式”类推也是大多数学生自己想不到的，不是自己“生长”的结果。

二、教学新设计

鉴于以上课程编排存在的问题，笔者对一个数除以分数的法则推导这部分内容的教学重新进行了设计和编排，创造性地设计了一种新的课程教学方案——从倒数的意义和乘除混合运算的计算规律入手进行推导。这是一种非常简便而又完备的数理证明方案。同时，笔者还保留了通过解决问题进行实证的编排内容（如北京版的推导方式），但是笔者把它后置到设计的课程之后，成为选学式的补充内容，为学生提供从另一种角度探索和理解的路径。把浙教版的第二种路径编辑为课外拓展阅读材料，后置到学生学会分数除法计算之后，并融入到学生证明整数、小数的商不变的性质适用于分数除法的发现之中。

笔者的这个课程和教学设计，经过课堂实践，收到非常好的教学效果。下面，将课程和教学设计简述如下：

模块一：畅想算法。（单独一页，第一页）

学生自己想办法尝试计算下面各题，看看能想到多少种不同的算法。（单独一页，留足空间，让学生尽情畅想和创造）

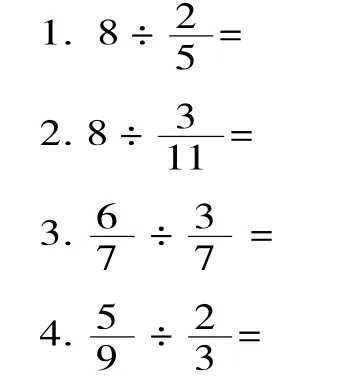
实际教学中学生尝试结果如下：

第1题全部学生都想到了把分数化成小数，顺利完成了计算。第2、3、4题一部分学生尝试把分数化成循环小数，不能解决；一部分学生把分数化成小数后，取近似值，算出近似的商。全体学生遇到“化成小数不行”这个障碍后都能正确得出第3题的结果，并能从里包含里有2个，或者推出商是2。部分学生受此启发自觉把第2、3题化成同分母分数，转化成了分数单位个数的相除；没有学生使用“把被除数和除数同时扩大相同倍数使除数变成1”的策略；更多的学生通过提前预览教材、父母教学以及通过其他途径“知道”除以一个分数可以变成乘以这个数的倒数来计算，但是不能解释为什么可以这样算。

模块二：发现规律，寻找证明途径。（单独一页，第二页）

激励性过渡导语：完成下面的这个“发现”项目，你就能解释为什么“除以一个分数可以变成乘以这个数的倒数”。

1.下面的题目除了按照从左到右的顺序外，你还可以怎样计算？

78×5÷5 43×24÷12

32×1÷0.517×1÷0.25

39×1÷10

2.你有什么发现？

（先乘后除的混合运算，可以先除后乘，结果不变）

3.自己举例试一试。

4.变式应用。

14÷0.5还可以怎样计算？为什么？31÷0.1呢？1.1÷0.2呢？

在实际教学中，学生都能正确转化成乘法进行计算，并能条理正确地解释和阐述自己的推导过程：如14÷0.5=14×2，因为14÷0.5=14×1÷0.5=14×（1÷0.5）=14×2。

模块三：证明一个数除以分数的统一算法。（第三页）

1.根据上一页你发现的规律想一想，如果把1.1÷0.2改成，你还可以怎么算？

3.思考：甲÷乙 =？（乙≠0）可以怎样算？

学生顺利完成自己的一般化的推理过程：甲÷乙=甲×1÷乙=甲×（1÷乙）=甲×乙的倒数（乙≠0）。

模块四：自主研究或者自学其他推导方案。

学生可以根据自己的情况自己选择完成拓展探究：

1.自由研修：尝试独立探索其他能证明“甲÷乙=甲×乙的倒数（乙≠0）”的方法。

2.必选研修：提供“北京版教材（六年级上册第18、19页）和浙教版教材（五年级下册第56、57页）的复印页，学生自选一种版本（或两种都选），自学这种版本教材的推导方案，并能给同学们讲明白。

三、课后反思与评价

经过课后反思，笔者认为这个课程和教学设计实现了以下五点预期目标：

1.学生在模块一中，自己畅想和尝试多种算法，亲身经历和体验了算法的多样化，他们能从不同的算法中得到智慧的启迪，增强了从不同的角度解决问题的意识和能力，激发了学生的主动性和创造性，同时各种方法之间又能互相证明。

2.这个课程和教学设计真正打通了除法运算和倒数意义的内在关系。倒数的意义是“乘积是1的两个数互为倒数”，即“1除以任何不为零的数就得到这个数的倒数”，甲÷乙=甲×1÷乙=甲×（1÷乙）正是对学生前面学习倒数的真正充分的应用。加深了对倒数意义和学习价值的认识，体现数学知识之间的内在联系与和谐之美。

3.这个课程和教学设计真正实现了——利用数学内在概念和规律（倒数的意义、乘除混合运算顺序的规律），从数理的角度（即从“数学→数学”的角度）进行简洁、完备、严谨的逻辑推理和证明。它和后置的从实际问题出发的实证，即从“生活→数学”互相补充和印证，形成了一个完整的证明系统，让学生对“一个数除以分数”的计算法则有了更为立体、完整的全景认识和理解。

4.这个课程和教学设计简明易懂，教学中有利于学生自己去发现、去推导，学生理解也更深刻，掌握也更扎实。

5.模块四提供了可选择的拓展课程，让学生在从数学到数学的推理证明的基础上，又明晰了两种教材上的“从生活到数学的数学化过程”，进一步体会到可以从不同的路径证明和研究“除以一个分数等于乘以这个分数的倒数”，体验到多角度地刻画和思考的分散和统一之美，感悟到数学学科的逻辑性、严谨性。同时，也能在一定程度上实现“让不同的学生在数学上获得不同的发展”的理念，在一定程度上关照到了学生学习数学的个性。