让“形”成为学生学习数学的拐杖
2017-04-02刘桂玲
刘桂玲
数学是一门抽象思维较强的学科,小学生的思维特点是以形象思维为主,他们获取的绝大部分数学知识首先是在对形象感受、感知的基础上逐步建立起表象。赞科夫曾说:“教会学生思考,这对学生来说,是一生中最有价值的本钱。”而要教会学生思考,实质上是要教会学生掌握数学的思想方法。常用的数学思想方法有很多,而数形结合思想具有数学学科的鲜明特点,是解决许多数学问题的有效思想。因此在教学实践中,可以让“形”成为学生学习数学的拐杖,使学生感受到数学很简单,数学很有趣,从而提高学生学习数学的内驱力。
一、基础知识教学中,利用“形”助理解和记忆,掌握换算规律
《数学课程标准》指出:“要使学生形成解决问题的一些基本策略,体验解决问题的策略的多样性,发展实践能力和创新精神。”我觉得在培养学生创新精神的同时,教师也应该勇于创新,创造性地用“形”来帮助学生理解知识,使其知其然更知其所以然。
在教学单位换算时,我发现通过一次次的练习,学生当时能够总结出单位换算的规律,但在实际应用时,还常常出错,究其原因,是对单位换算的规律不理解,所以只靠死记硬背是不行的。所以我利用天平的平衡原理,帮学生理解大单位变小单位要乘进率,小单位变大单位要除以进率的道理。
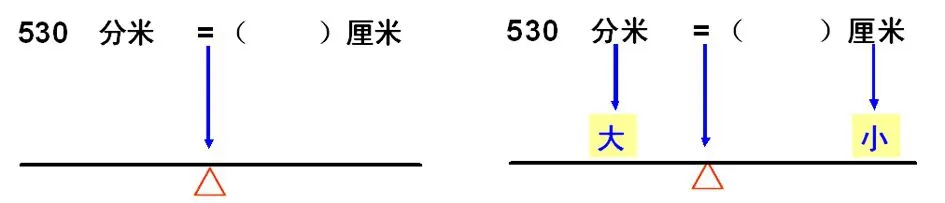
比如530分米=( )厘米,“=”就相当于天平的支点,两边的单位就相当于两边的盘子,先让学生比较两个单位的大小,分米(大),那它前面的数就要(小),厘米(小),它前面的数就要(大),所以换算530分米=( )厘米时,要乘进率,等于5300厘米。

利用天平的平衡原理进行解释,学生们很容易掌握单位换算的方法和窍门,而且越来越喜欢上单位换算,准确率也大大提高。
再如在教学求近似数时,我利用数轴直观地帮助学生理解求近似数的方法,首先出示数轴,标上数字,从0——10,从10——100,从100——1000,让学生找中点,学生很快找出中界线,为后面学生发现规律做好铺垫。

接着我出示一个数轴,逐步出示508、517、525、538、543;597、582、576、564、556,让学生分别说说这些数离500近,还是离600近,可以看成哪个整百数。有了分界线学生很好做出判断,并总结出在分界线前面的数要估成比它小的近似数500,在分界线后面的数要估成比它大的近似数600,这样为以后学习“四舍五入”法求近似数打下坚实的基础。
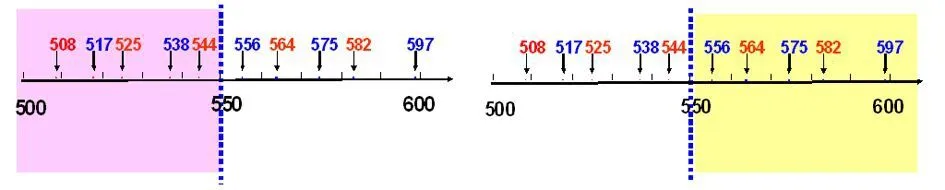
数学语言比较抽象,学生看过、听过不容易记住,而图形语言则比较形象,能快速帮助学生理解知识,牢固地掌握解决问题的方法。
二、计算教学中,利用“形”化抽象为直观,理解算理与算法
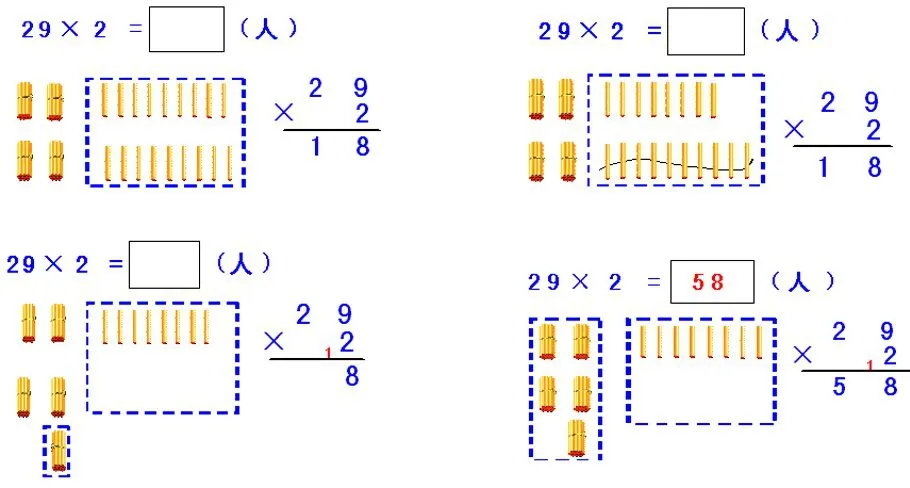
在小学阶段,计算所占的比重很大,学生的计算能力的高低直接影响着学生学习数学的质量,而“加减乘除”比较抽象,学生不易理解,而数形结合则是帮助学生正确理解算理,明确算法的一种很好的方式。如教学《两位数乘一位数(进位)笔算》时,通过摆小棒帮助学生明确9×2=18,18满十,就把10根小棒捆成一捆。与2个十×2=4个十合起来就是5个十,让学生形象、直观地感知进位数1是从哪里来的,借助小棒,既明确了算理,又掌握了算法。
在教学《两位数乘两位数(不进位)笔算》时,借助点子图拆分,把两位数乘两位数转化成以前学过的两位数乘一位数和两位数乘整十数,沟通了图形表征、算式表征和计算方法之间的联系,使数和形有机结合,让学生对算理的理解有“形”可依,进而在头脑中建立起清晰的三步有序过程,充分地体验了由抽象算理到直观算法的过渡和演绎过程,进而达到对算理的深刻理解和对算法的真正掌握,促进学生数学思维的发展。

三、解决问题中,利用“形”助分析与思考,建立解决问题的模型
在教学《求比一个数的几倍多几的数是多少》一课时,学生第一次真正地接触线段图,如果直接引入线段图进行分析,对于学生来说太过生硬,难以接受和理解。所以我想到变化,先摆纸条,将复杂的信息和问题明确化,(一年级转呼啦圈的有18人,二年级的人数比一年级的2倍还多5人,二年级转呼啦圈的有几人?)
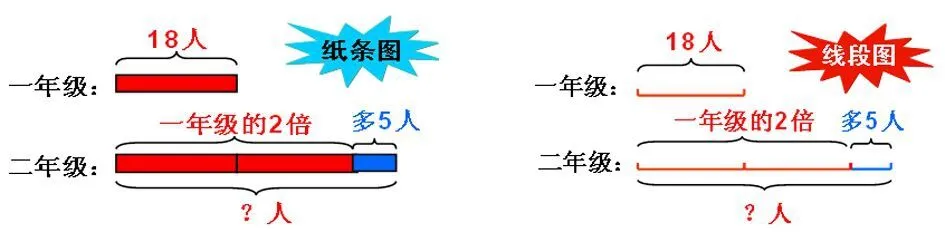
这种方法可以减少学生认知线段图的坡度,再由纸条图自然过渡到线段图,然后引领学生读图,明确线段图能够整理出所有的信息和问题,初步建立线段图的表象,接着让学生尝试画线段图。通过交流比较,让学生体会线段图产生的必要性与合理性,充分经历从“纸条”到“线段图”的抽象过程,让线段图成为学生一种内在的心理需求,帮助学生学会用线段图整理信息和问题,进而引导学生结合线段图分析数量间的关系,使学生认识到线段图不但可以整理信息和问题,还可以帮助分析数量关系。在理顺数量间的关系后,透彻分析解决问题的“骨架”,明确求比一个数的几倍多(少)几的数是多少,需要先求一个数的几倍,再求多(少)几的数,逐步建立解决问题的数学模型。并在练习中进一步巩固,达到使学生不但能把文字转化成线段图,还能根据线段图说出信息和问题,巧妙地将线段图融入到学生的数学思维中,深深印入到学生的心田,使学生在今后的学习中能够根据解决问题的实际需要,合理地选择和使用这一策略方法,培养学生分析问题的能力,使学生由“学会”转变成“会学”。做到建立模型,分析有据;掌握方法,分析有路;运用策略,分析有法。
华罗庚先生说过:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休。所以,在数学教学中,我们要从低年级教学开始渗透、融合、培养学生的数形结合思想,使学生脑中有“形”,见数想“形”,为学生打开一扇学习数学的窗,授之以渔,培养学生的创造性思维能力。数形结合就像学生建构知识的一个拐杖,有了这根拐杖,学生才能走得更稳、更好。
