经历概念形成走向数学本质——《认识百分数》教学实录与说明（一）

荆亚琴

【教学内容】

苏教版六年级上册第84、85页，练习十四第1、3题。

【教学过程】

一、创设情境，感知百分数的意义

1.分析比较，引入百分数。

师：王老师记录了学校篮球队三场比赛中的投篮情况。可以怎样比较？同桌交流。（多媒体呈现第84页表格）

生：我比较的是投篮次数，第三场比赛中投篮次数最多。说明学校篮球队在第三场比赛中抢球投篮非常积极。

生：我比较的是投中次数，第三场比赛中投中次数最多。

生：我比较的是投篮命中率。先计算出每场比赛投中次数占投篮次数的几分之几，再进行比较。

师：我们可以比较投中次数占投篮次数的几分之几来评价三场比赛的投篮水平。请同学们独立计算出每场比赛投中次数占投篮次数的几分之几，再比一比，并与同学交流。

呈现学生的比较方法：

师：你更喜欢这三种中哪一种比较方法呢？（多数同学表示更喜欢3号同学的比较方法）

师：为什么大家喜欢都化成分母是100的分数呢？

生：1号同学只是求出了投中次数占投篮次数的几分之几，但没有通分，所以不好比较。

生：2号同学虽然也是通分，但分母太大，通分时易出错。

师：既然公分母是300，为什么3号同学却是以100为公分母呢？100是怎么来的？

师：把原来的分数先约分，再通分，是一种好办法。为便于统计和比较，通常把这些分数化成分母是100的分数来表示。

根据学生发言，完善板书：

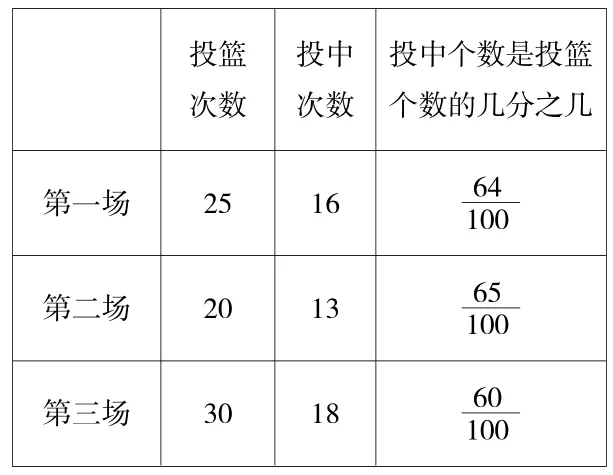
第一场 25 16 64 100第二场 20 13 65 100第三场 30 18 60 100投篮次数投中次数投中个数是投篮个数的几分之几

师：剩下的两个分数，同桌互相说说它们的含义。

【说明：通过创设篮球比赛的情境，提出“可以怎样比较这三场比赛的投篮情况？”开放的问题，学生在解决问题的过程中会有更多样化的视角，在碰撞交流中得到启发、提升。例题以概念形成的方式帮助学生获得对百分数概念的认识。学生在比较投中次数是投篮次数的几分之几的过程中，有的同学以300为公分母，有的同学以100为公分母，在交流中，学生感受到化简后通分为公分母是100的分数更方便比较。让学生解释每个分母是100的分数所表示的具体含义，就是让学生经历抽象与概括的过程，初步形成百分数概念。】

2.教学百分数的读写。

师：生活中，百分数通常不写成分数形式，而是在原来的分子后面加上“%”表示。如写作64%，读作百分之六十四。请同学们先将其余两个分数改写成百分数，再完成下面的练习。

多媒体呈现：

（1）百分之一百三十；

（2）百分之零点五；

（3）7.5%；

（4）125%。

（学生独立完成，全班交流，重点交流7.5%的读法）

生：一百分之七点五。

师：他读对了吗？

生：应读作百分之七点五。

师：我们在读百分数时，要读作百分之多少，不能读成一百分之多少，这和分母是100的分数读法有一点不同。

教师结合反馈，完善板书：

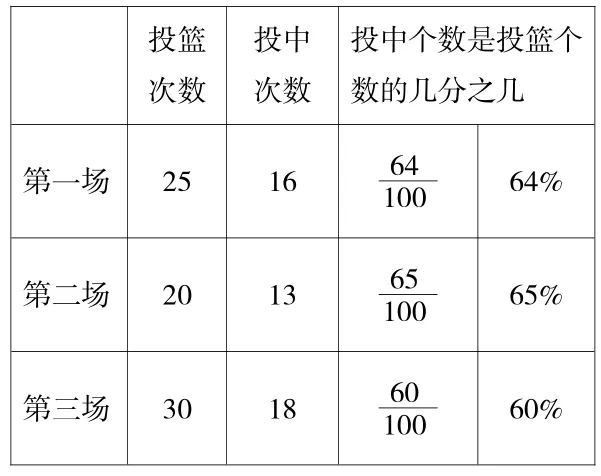
投中个数是投篮个数的几分之几第一场 25 16 64 100 64%投篮次数投中次数第二场 20 13 65 100 65%第三场 30 18 60 100 60%

师：表格中的百分数分别表示什么意思？（全班交流）

【说明：教材中呈现的都是分子小于100且为整数的百分数，这些百分数学生在生活中常常见到，多数学生会读、会写。但是分子为小数或大于100的百分数，学生读写却有困难。因此，以7.5%为抓手，重点交流分子为小数的读法，通过交流与示范帮助学生掌握百分数的读法和写法。】

二、对比感悟，丰富内涵

1.沟通联系，理解百分比、百分率。

（多媒体呈现85页试一试）

师：我们初步理解了百分数的意义，请同学们根据百分数的意义填空，再同桌交流对这些百分数的理解。（学生独立填写，同桌交流，教师巡视）

师：这三个百分数分别表示什么意思？

生：45%表示学校合唱队中男生人数是女生人数的45%。男生人数是女生的，男生和女生人数的比是45∶100。

生：75%表示已经装船的货物是货物总量的75%。已经装船的货物与货物总量的比是75∶100。

生:20%表示全班中有20%的同学是近视。

师：既然百分数表示一个数是另一个数的百分之几，你能具体地说说是哪两个数在进行比较吗？

生:20%表示近视的人数占全班人数的20%。

师：抓住近视人数和全班人数这两个数的比较就容易知道20%这个百分数的意义。

多媒体呈现：姚明加盟NBA联赛的第一年，投篮命中率为49.8%。

师：这里49.8%表示什么意思呢？

生：是指姚明投中次数占投篮次数的49.8%。

师：如果姚明投了100次球，是不是可以说他投中了49.8次球？

生：不可以。这里的49.8%只是表示姚明投篮的命中率是49.8%。

生：这个百分数表示姚明投中次数和投篮次数的倍比关系。可以说姚明投中次数和投篮次数的比是49.8:100。

师：看来，49.8%代表的并不是具体的次数，而是投中次数和投篮次数相比的一种关系。生活中有近视率、命中率，你还见过哪些百分率？

生：体育课上，老师会统计同学们的达标率、优秀率。

生：我爸爸工作车间会统计生产零件的合格率。

师：说得真好。百分数表示的是两个数（量）之间的比率，所以百分数又叫百分比、百分率。

【说明：教材“试一试”的三个习题，是百分数在生活语境中的不同表达方式。从完整的百分数表达到简略的百分数表达，学生逐步理解不同语境中百分数的含义。学生前期虽然有百分数的意义作为继续学习的基础，但学生对百分数与比之间的联系、百分数为什么又可以叫作“百分比”“百分率”，在理解上还存在困难。通过练习转化，让学生体会百分数表示两个数（量）之间的倍比关系，百分数相当于后项是100的比。百分数、百分率都是表示两个数之间的倍比关系，而不是指具体的一个数，从而加强学生对百分数意义的理解。】

2.结合实例，丰富百分数的内涵。

师：生活中还有很多百分数，老师也带来了一些百分数，先自己读一读，再小组交流。（出示练习十四第1题）

师：怎么理解这些百分数？

生：40%表示会游泳的同学占全班同学的40%。

生：50%表示苹果汁含量占全部饮料的50%。40%表示葡萄汁含量占全部饮料的40%。

师：由这两个百分数还能联想到什么？

生：我联想到这瓶饮料中的其他成分占全部饮料的10%。

生：我联想到葡萄汁含量与苹果汁含量的比是4:5。

师：真棒！百分数不仅方便比较，还能让我们联想到其他的信息。

生：羊毛含量占这件衣料的100%。100%可以看出这是一件纯羊毛衣料。

师：你还在哪里见过100%？

生：我在牛奶盒上看到过100%纯牛奶。

生：我在餐巾纸袋上看到100%纯纸浆。

师：看来，100%在生活中的运用也很多。请同学们拿出课前收集的百分数，这些百分数又分别表示什么意义呢？

活动要求：

（1）每位同学在小组里交流自己搜集到的百分数，先读一读，再说一说百分数的含义。

（2）每个小组选择一个百分数全班交流。

生：这个百分数是爸爸告诉我的。他们车间技术革新，现在产量是原来的120%。120%表示现在产量是原来产量的120%，说明产量提高了。

生：我们班跳绳优秀率是75.3%。表示我们班跳绳的优秀人数占总人数的75.3%。

……

师：上面的例子中，情境不同，百分数大小也各不相同，有什么相同的地方呢？

生：百分数都可以用来表示两个数之间的倍比关系。

师：对，用百分数表示一个数是另一个数的百分之几。

【说明：概念类似于工具，只有在“使用”中才能被完全理解。“使用”蕴含着与该概念的情境发生关联。上述练习情境中所包含的学习材料真实亲切、源于生活实际，具有丰富的现实背景。借助练习，教师将教材中静态的知识过程化，建立百分数与使用情境之间的结构化关联。拓展概念外延以深化对概念内涵实质的把握，从而加深对百分数本质的理解。】

三、分层练习，深化认知

1.结合图形，理解百分数的意义。

（多媒体出示练一练第一题，学生独立练习，教师巡视）

师：看了百格图，你有什么发现？

生：我发现涂色部分和空白部分合起来是100%，即“1”。

生：我发现随着涂色部分越来越多，没涂色部分就越来越少。涂色全部涂满，也就是“1”。

师：同学们说的都很有道理，那么在这个正方形中，涂色部分可以占“1”的105%吗？

生：不可以。因为即使全部涂满也只有100%。

师：但为什么我们找的例子中就有超过100%的百分数？

生：在百格图中，涂色部分是“1”的一部分，即使涂满，也只能是100%。

生：现在每月产量和原来每月产量是两个不同的量，车间技术革新，现在比原来生产的多，所以可以超过100%。

师：如果百分数只是表示部分和整体之间的倍比关系，这个百分数最多达到100%。而车间生产，现在产量和原来产量是两个独立的量，当这两个独立的量进行比较时，百分数就可能超过100%。

【说明：以“百格图”作为支撑，通过数形结合，引导学生再次理解百分数的意义，从而使抽象的问题直观化、生动化，有助于学生把握百分数的本质。同时，通过讨论“涂色部分可以是正方形面积的105%吗”，让学生理解表示部分与整体之间的倍比关系时，百分数不能超过100%，表示两个独立的数（量）之间的倍比关系时，百分数可能会超过100%，学生对百分数有了更深的理解。】

2.新旧比较，沟通分数和百分数的联系。

师：我们认识了百分数，是不是分母是100的分数都可以改写成百分数的形式？把下面能改写成百分数的写在题目后面的括号里，再同桌交流百分数和分数有什么联系和区别？（多媒体出示练习十四第三题）

生：百分数只表示一个数是另一个数的百分之几。而分数还可以表示一个具体的数。

师：分数既可以表示两个数之间的倍比关系，也可以表示具体的数量，而百分数只表示两个数的倍比关系。所以，百分数是特殊的分数。

【说明：分数是“上位概念”，百分数是“下位概念”。分数既可以表示一个具体的数，又可以表示两个量之间的关系。而任何一个分母为100的分数要成为百分数（百分比，百分率），都需要一定条件，没有任何条件和语言环境的分母是100的分数一定不是百分数（百分比、百分率）。把分数、百分数这两个新旧概念进行辨析比较，使百分数这个概念与已有认知结构中比较稳定的分数概念建立实质性联系，通过将百分数这一新概念纳入原有认知结构，从而形成新的认知结构。】

3.灵活选择，提升判断、选择意识。

多媒体出示：

106.6% 45% 98%

99% 100% 55% 0.5%

（1）我国神舟飞船从神舟一号到神舟七号发射全部成功，发射成功率是（）。

（2）一个工厂从一批产品中抽出100件，经过检验，有99件合格，合格率是（ ）。

（3）2017上半年，某品牌电视机销售收入稳步增长，上半年销售收入是去年同期的（ ）。

（4）某品牌牛奶是由新鲜牛奶制成，特浓牛奶脂肪含量在3.7%～4.2%之间，脱脂牛奶的脂肪含量低于（ ）。

（学生独立完成，教师巡视）

师：谁来说说你的想法？

生：第一题，我选择100%。因为每一次发射都成功了，所以成功率是100%。

生：第二题，生产的100个零件中有99个零件是合格的，合格率我选择99%。

生：第三题，因为销售收入稳步增长，上半年的销售收入肯定比去年同期多，在这里106.6%这个百分数超过了100%，所以选择106.6%更合适。

生：第四题，特浓牛奶的脂肪含量是在3.7%～4.2%之间，脱脂牛奶的脂肪含量应该比3.7%低。在这里只有0.5%比3.7%低，所以我选择0.5%。

师：同学们的想法都很有道理。看来，今天同学们不仅认识了百分数，还能活学活用。

【说明：在教学中，教师不仅应关注到让学生经历“数学化”，更应关注学生判断与选择意识的培养，学生整体综合与灵活敏捷的思维品质的提升也是数学概念教学中需要关注的。数学概念教学应以学生的敏感反应、准确判断和灵活选择为前提。因此，该练习重在让学生自主判断，自主选择。】

4.综合应用，认识百分数的本质。

师：接下来，我们就来玩个小游戏。

出示游戏规则：在1分钟内完成口算。当听到铃声，立即停笔，学生独立完成，同桌互相检查。

师：如果我们以十道题为标准量，请你用百分数来说一说你完成的题数。

生：我做了80%的题目，我做对了100%。

师：为什么第一个是用80%表示，第二个却用100%表示呢？

生：第一个80%是把完成的八道口算题和十道口算题比较。100%是把做对的八道口算题和完成的八道口算题进行比较，所以百分数不同。

师：请完成十道题或十道题以内的同学举手示意。你完成了多少道题？

生：我完成了十二道题。

师：他完成了标准量的百分之多少？

生：他完成了标准量的120%。

【说明：帮助学生在具体的数与抽象的百分数之间实现相互转换，达到将抽象的数学问题具体化的效果。让学生在应用中加深对百分数意义的理解，有助于学生更好地认识百分数的本质。学生在富有挑战性和趣味性的问题情境中学习数学，思维的积极性将得到提高，帮助学生形成主动学习的习惯。】

四、总结回顾，提升认知

师：通过这节课的学习，你能用一个百分数来谈一谈你今天的收获或感受吗？

生：我今天上课有些紧张，大约占10%。

生：今天学习的知识，我100%听明白了。

【说明：学生用百分数表达自己本课的收获或感受，既有意识地让学生回忆和总结所学的知识，又在应用中再一次加深对百分数的理解。】