学会“挖井”思维
2017-04-02任卫兵特级教师
任卫兵(特级教师)
【教学内容】
苏教版六年级上册第21页。
【教学过程】
一、出示习题
(出示数学书第21页的一道习题)
用1立方厘米的正方体木块堆成的两个长方体,分别正好装满各自右边的容器。你知道这两个容器各能盛多少毫升水吗?

师:要比较两个容器的容积大小,如果不测量和计算,我们可以怎样比?
师:为了便于表达,我们可以把左边的容器叫做甲容器,右边的为乙容器。谁来说说你的想法?
甲

乙
师:把甲容器装满水,倒入乙容器,可能会出现几种情况?
生:第一种情况,甲容器倒空,乙容器未满,乙容器的容积大;第二种情况,甲容器倒空,乙容器正好装满,甲、乙容器的容积一样大;第三种情况,甲容器未空,乙容器装满,甲容器的容积大。
师:无论是上面的哪一种情况,两个容器中水的体积和总是怎样的?
生:两个容器中水的体积和是不变的。
【设计意图:在学生学习了《长方体和正方体》单元知识后,需要对本单元进行一次整理和复习。通过知识梳理和变式练习是一条路径;借助书本习题,引导学生从不同的视角挖掘出新的问题,从而将相关知识有机统整到一起,则是另一条路径。后一种路径比起前一种来,可能更具挑战性,更易激发学生的问题意识和探究欲望。】
二、拓展练习
拓展一:
师:现在我们从里面测量了甲容器的长是6厘米,宽5厘米,高(或深)4厘米,乙容器长7厘米,宽3厘米,高5厘米。
师:我们把甲容器装满水,再倒入乙容器。装满后,你们能提出哪些问题?
生:甲容器中剩下的水的体积是多少立方厘米?
生:甲容器中剩下的水的高度是多少厘米?
生:甲容器中剩余部分的空间有多大?
师:同样把甲容器装满水,再倒入乙容器。但这一次不倒满,如果要使两个容器中的水面一样高,你们能求出现在两个容器中的水深都是多少厘米吗?
(全班交流,请小组代表介绍各自的解决方案)
第一种想法:因为两个容器中水的体积和是不变的,还等于原来甲容器中的水的体积,所以我们可以列方程来解答。解:设现在两个容器中的水深都是x厘米。5×6×x+7×3×x=5×6×4。最后求出这个方程的解是。
师:两个容器中水的高度是一样的,我们都用字母h来表示,底面积不同,分别用字母S1、S2来表示,那么两个容器中水的体积和就可以用什么来表示?(S1h+S2h)还有其他的表示方法吗?
生:还可以应用乘法分配律,用(S1+S2)h 来表示。
师:那如果不列方程,还可以怎样求现在两个容器中的水深呢?
第二种想法:我们可以假设把两个容器粘在一起,然后抽调中间的隔板,再把水重新倒入这个特别的容器中。用原来甲容器中水的体积,除以两个容器的底面积的和,也可以求出现在的水深。列式为(5×6×4)÷(5×6+7×3)。
师:刚才的两种解法,如果细细观察,还是能发现它们之间是有联系的。有兴趣的话,课后还可以从“比”这个角度去想想其他的一些解法。
【设计意图:在比较两个容器的容积大小时,如果不测量和计算,而用倒水的方法来比较,那么可能会有几种不同的情况呢?引导学生全面地思考问题,需要自然、无痕地进行渗透。在学生列举出所有可能的情况后,教师适时地总结出无论哪一种情况,两个容器中的水的体积和是不变的,这也为接下来解决“两个容器中的水深相等”这一问题做了铺垫。教会学生“挖井”思维,需要教师适当地为学生铺设一个台阶,确定一个大致方向,这样才便于学生积累一定的经验。只有当学生有了自己的经验后,别人的经验才能够接得上去。】
拓展二:
师:刚才我们是从体积(容积)这个角度来提出、解决新问题的,下面我们换个视角,来看这两个长方体,你们又能提出哪些新问题呢?
课件出示:
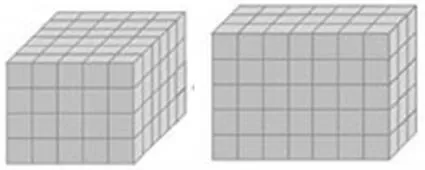
师:如果把这两个长方体表面涂漆,再切成1立方厘米的小正方体,那么三面、两面、一面涂色以及六个面都未涂色的小正方体各有多少个呢?你们觉得这个问题与“表面涂色的正方体”有哪些相同之处?又有哪些不同呢?
师:同桌两人分工,一起来算一算:把第一个长方体切开后,各种涂色小正方体的个数。
【设计意图:从“表面涂色的正方体”拓展到“表面涂色的长方体”,不仅能让学生更好的掌握长方体和正方体的特征,更有利于学生建构相应的模型,积淀数学思想。】
拓展三:
1.比较这两个长方体,你还有什么不同的发现?
(适当提示:刚才我们分别从体、面这几个角度发掘出了新问题,如果从棱的角度呢?)
2.大家注意到没有,这两个长方体的棱长总和怎样?(都是60厘米)根据这一特点,你又能提出什么新问题呢?
(棱长总和是60厘米的长方体,体积最大是多少?最小是多少?)
师:还可进一步提炼为棱长总和相等的长方体或正方体,谁的体积最大?
3.寻求策略。
师:棱长总和是60厘米的长方体,有多少种不同的情况?解决这类问题适合采用哪种策略?
(那我们可以从哪一种情况开始列举呢?)
4.合理猜想。
师:通过不完全列举,你能提出什么猜想?
(棱长总和相等的长方体和正方体,正方体的体积最大。)
【设计意图:也许教材编写者也没有意识到书本习题中的两个长方体的棱长总和恰好相等,教师敏锐地捕捉到了这一特点,引导学生提出问题“棱长总和相等的长方体和正方体,谁的体积大”,并通过有序列举、不完全列举,启发学生大胆地提出自己的猜想。可见,“大问题教学”并非一定要确定一个多大、多综合的问题,有时一个小问题一样能作出大文章。】
拓展四:
如果这是一个封闭容器,不小心在它的前面破了个洞,洞口下端距底面2厘米。这个容器最多能装水多少毫升呢?
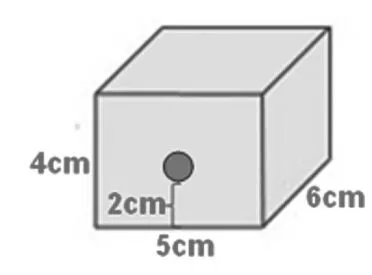
师:有认为能装水60毫升的同学吗?还有不同的答案吗?说说你是怎么想的?
【设计意图:学会“挖井”思维,并非一味地求综合、求深入,有时还要学会应变。一个有破洞的容器最多能装多少水,如果固守着底面不变,那么只能得到60毫升的结果,可是如果能灵机一动,把容器翻转一下以后面作底面,让洞口朝上,那么最多就能装水120毫升。不仅能入乎其内,还要能出乎其外,学会知入知出,才能彰显出智慧。】
三、总结
师:通过这堂课的学习,你们对“学会‘挖井’思维”又有了哪些新的体会?(同一个问题,换个角度去看,就会有不同的发现)正所谓:思维一变天地宽,知入知出显智慧。
