重视直观感受丰富形象思维
——《角的初步认识》教学实录与分析
2017-04-02许频
许 频
【教学内容】
浙教版三年级上册第84、85页。
【教学内容】
本文是笔者根据人教版二年级下册《角的初步认识》和浙教版三年级上册《角的初步认识》的内容编排,结合学生的实际情况,对教学内容做的一些整合。基于学生此前已初步认识了长方形、正方形、三角形和平行四边形等平面图形,对生活中的角也有初步的感知,教学设计从学生熟悉的图形中引出角,从观察比较、动手操作等活动中初步认识角、学会用尺子画角,用学具做角,感受角的大小与边张开合拢有关系,体会数学的现实价值、应用价值。
环节一:猜想图形,揭示课题
师:今天老师请到了4个图形。请你来猜猜看,它们分别是什么呢?
(课件出示)

生:第一个是五角星。
师:你是怎么猜出来的?
生:看到露在外面的尖角。这个图形露出了5个角,所以是五角星。
生:第二幅图有三个角就是三角形。
生:第三个是长方形,因为有四个角,而且都是方方正正的角。
生:第四个是圆形,因为圆形没有角。
师:我们发现有些图上有角,有些图上没有角,“角”能告诉我们一个图形的很多秘密。今天这节课我们就一起来研究和认识“角”。(出示课题)
【分析:从学生已学过的平面图形入手,开门见山,揭示课题。这样既可以避免“生活中的角”对于“数学中的角”的一些干扰,又体现出“角”是平面图形的重要组成部分,刻画了图形的重要特征。根据学生的认知特点,特意把五角星放在第一个出现,让学生有意识地通过观察图形的角来判断这个图形可能是什么形状,直接、有效。】
环节二:动手操作,探究新知
1.抽取角,初步感知。
师:为了方便研究,老师把这些角从图形上取下来(图形隐去),并把它们全部放在一起。
(出示下图)
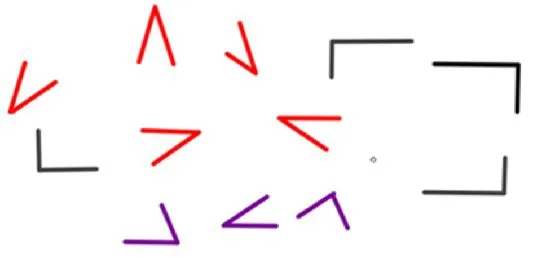
2.找相同,抽象角的特征。
师:你们看这么多角,他们有什么共同的特征呢?
师:都有一个尖尖的地方,你们发现了吗?
师:这个尖尖的地方是一个“点”,在数学上我们称为角的“顶点”。(板书:顶点)
师:还有两条线——这两条线也有名称叫做角的两条边。(板书:两条边)
小结:角是由一个顶点和两条边组成的。
【分析:通过把“角“从平面图形上“取”下来的过程,使学生能够直观的看到角和这些平面图形间的联系。让他们知道角其实就是图形的一部分,只是为了观察方便才取下来的。在取下来的同时刻意打乱了顺序,让学生看到形状、开口、边长各不相同的角,同时放手让学生自己去观察和交流,比较变式图形来概括图形的本质特征——“一个顶点、两条边”。在明确“角”的各部分名称之后再增加一个“边指边说”的环节,以便巩固。】
3.判断角,游戏中完善角的特征。
师:接下来我们来玩一个游戏,看看哪些同学的反应最快,一会儿屏幕上会出现各种图,是角的,请你起立,不是角的,请安静坐着。
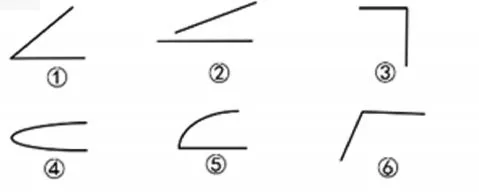
(学生用行动汇报:①③⑥是角)
师:为什么这几个都是角?请说一说你的理由。
生:因为他们都有一个顶点和两条边。
师:如果把⑥像这样旋转一下,还是角吗?这样呢?为什么还是角呢?
小结:不管怎么旋转,只要有一个顶点和两条边的就是角。
师:④⑤为什么不是角呢?
生:因为边不直。
师:②为什么不是角呢?它的边不是直直的吗?
生:因为两条边没有碰到一起,没有顶点。
小结:通过刚才的游戏我们发现角不仅有一个顶点、两条边,而且边是直直的。
【分析:学生都很喜欢游戏。在感知了角的基本特征之后,设计了判断正误的游戏环节,而判断的过程就是巩固和完善角的特征的过程——顶点,即两边交于一点;两条边要直直的。通过这个环节,学生对角的认识从整体感知走向了分析落实。】
4.画角,巩固角的特征。
师:(边板演边说)先画一个顶点,再沿着顶点画两条直直的边,这样就形成了一个角。
师:请你在练习纸上,用尺子把你想象中的角画下来(画一个),看谁画得又对又快。
师:你跟同桌画的角一样吗?有什么不一样的地方?
生:大小不一样。
生:边的长短不一样。
生:开口方向不一样。
师:既然有这么多不同,为什么画的还都是角呢?
生:因为它们都有一个顶点,两条直直的边,所以都是角。
师:大小、方向都不重要,重要的是角都有一个顶点,两条直直的边。
【分析:通过动手“画角”这个环节,进一步直观地巩固了角的基本特征。从教学节奏上讲,与前面游戏环节的“起立、坐下”相比,是从肢体大动作到手指小动作,使课堂渐渐安静下来,从认知上和情绪上为接下来重点体会角的大小做好准备。】
5.创造角,初步感知角的大小。
师:刚才我们看过角、判断角、也画了角,角还可以怎么“玩”呢?大家做一个角好不好?老师手上有一些材料,请你先想想看可以怎么用这些材料来做角?
(出示纸条、图钉、橡皮)
生:纸条当作边,图钉当成顶点。
师:你想的真不错,角的顶点和边都有了(边说边做)。为了不让图钉扎手,我们可以用橡皮把图钉封牢,一个可以活动的角就做好了!(活动角的两边)我们把它叫做“活动角”。请你也来做一个活动角,并把它举起来。
师:老师这里也有一个活动角,请你看仔细,我要变魔术啦。把这两条边张开再张开,现在我的角越来越——(大),合拢再合拢呢,我的角越来越——(小)了。
师:谁能变一个比我这个角大一些的角?为什么你觉得你的角比我的大?
生:因为我的角张开的比你大。
师:也就是说你是看开口的,开口大角就大!如果想变得再大一些呢?再变大一些呢?
生:把两条边再往外拉开一点,开口就能变大一些,角就大了。
师:谁能变一个比我的角小一些的角?
生:把两条边往里合拢一些,像这样就可以了,开口小了,角也小了。
师:那你们觉得角的大小和什么有关系?
生:与两条边的开口大小有关,两边张开越大角越大。
小结:角的大小和边张开的大小有关。(活动角演示)
【分析:通过自己动手制作“活动角“,再一次形象地巩固了角的基本特征:一个顶点,两条边。同时通过摆动“活动角”的两条边,真实、形象地感知到角的大小是指边的开合程度。为接下来深入思考“角的大小”的相关问题先做好概念性的铺垫。】
6.判断角的大小,巩固角的大小和边张开程度有关。
师:刚才我们用活动角摆了很多大小不一样的角,现在你能比一比这两个角的大小吗?
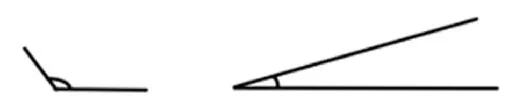
师:为什么第一个边这么短,角却大呢?
生:因为第一个角的开口大,开口越大角就越大。
师:这里也有两个角,你们觉得哪个大?可以怎么验证呢?
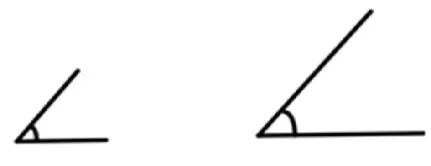
生:顶点对顶点,边对边。
师:你们发现了什么?
生:两个角,完全重合,所以两个角一样大。
师:如果老师把第一个角的边画长一些,他们还一样大吗?擦短一些呢?为什么还是一样大?
生:角的大小与两边张开的大小有关,和边的长短无关。
(板书:边张开的大小)
师:谁能帮我比一比这两个角的大小。(出示)

生:第一个角大。
师:可以怎么比较?
生:顶点重合。(出现顶点重合,一边在角内,另一边在角外的图)
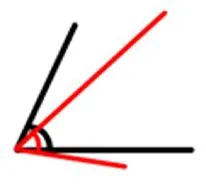
生:顶点重合,一边重合,看另一边。
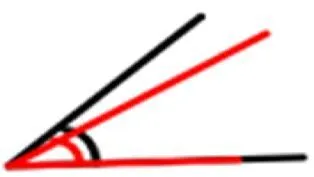
师:像这样顶点对顶点,其中一条边对齐,我们直接看另一条边就可以判断大小了。
【分析:在这个环节中设计了3个不同层次的比较角大小的活动。第一小题故意放大边的长短方面的特征,强调让学生排除边长短的干扰,强化前面定义的“角的大小”指两边张开的程度。两个角两边张开的大小显而易见,可以直接比较;第二小题,两个角的大小靠直接观看无法判断,引出重叠比较的需要。提供画有角的透明胶片,让学生通过自己的操作调整,感知角要如何重叠——顶点重合、边重合,建立角一样大的表象。同时通过延长和擦短的操作,为以后明确角的两边是射线,看到的只是画出的一部分做经验积累;第三小题,进一步聚焦重叠比较,进行方法上的突破,当两个角的大小不明显时,要在顶点重合,一边重合的前提下,比较另一边的位置。这一系列比较活动,为第二学段“识角”“量角”“画角”等做了充分的铺垫。】
环节三:课堂小结(略)
