小学数学概念教学中高阶思维的培养
——《角的认识》教学设计与反思
2017-04-02田秋月
田秋月
【教学内容】
浙教版四年级上册第51、52页。
【教学目标】
相较于其它版本教材,浙教版新思维《数学》所独有的四年级上册几何单元《角的认识》一课,清晰地体现了概念教学中对高阶思维的重视和培养。该课从角的静态(从一点引出两条射线所组成的图形叫做角)、动态(角也可以看成是由一条射线绕着它的端点旋转而成的图形)两个方向经历科学、规范、抽象的角的概念的探究过程。
安德森在其《认知目标分类学》中将思维区分为低阶和高阶,前者包括对知识技能的“回忆”“理解”“应用”;后者涉及“分析”“评价”“创造”,此外还强调“创造性思维”和“批判性思维”。
本文旨在通过这节概念教学课讨论高阶思维在具体课题教学活动中的实施,强调让学生经历实际操作、个体感悟,通过概念间的迁移,培养分析、评价、创造、反思的能力,实现高阶思维的提升。
【教学过程】

活动一:分析——静态角
1.观看微课视频,回顾三年级上册《角的初步认识》。
2.联系旧知,探究静态角。
师:(课件呈现一个点)从这个点出发,可以画多少条射线?
生:无数条。
(根据学生回答动态及时画出下图)

师:从这幅图中你看到了什么?
生:我看到了角。(上台指出一个角)
师:像这样的角还有吗?选一个画出来。
师:每位同学都画了角,那么你认为什么是角?
生:角是由一个点向任意位置发射出去的两条射线。
师:他的话里哪些词让你觉得特别重要?
生:一个点、两条射线。
(在教师引导下,角的静态概念描述为:角是从一点引出两条射线所组成的图形)
(学生将自己所画的角进行标识,集体反馈统一、优化角的标识方法)
【设计意图:以上教学设计体现了演绎推理的思想,通过分析已有事实和数学定理,推导出角的静态概念,它对人的思维严密性、一贯性有着不可替代的训练作用,为学生今后逻辑证明和定理推导的研究学习打下扎实的基础。在教师有意义的提问和任务指令下,培养学生准确、规范使用数学语言的能力,培养严谨的逻辑、分析全面的意识。】
活动二:评价——动态角
师:如果请你做角,需要什么材料?
生:两根小棒和一个钉子。两根小棒是为了做角的两条射线;用钉子固定,表示它是角的顶点。
师:请打开信封看一下,老师为大家准备的材料满意吗?怎么组成一个角呢?
(材料如图)

汇报:
方法1:(两条小棒不重叠)直接扣住顶点,这就是角了。
方法2:(两条小棒重叠)先扣住顶点,拉开两边,这样就是一个角。
方法3:(两条小棒重叠)先扣住顶点,一条射线不动,让另一条射线旋转,就可形成角了。
师:这三种方法你喜欢哪一个?它们之间有什么联系?
喜欢方法1:很简单,步骤少。
喜欢方法2:(用角的静态概念回答)从一个顶点引出两条射线可形成角。
小结:这两种方法本质相同,方法1中的“小棒不重叠”就是方法2中的“拉开两边”,本质上都是角的静态概念。
喜欢方法3:(用本单元刚学的“旋转”的知识来解释角)角是由一条射线绕着它的端点旋转而成的图形。
【设计意图:用“评价”贯穿整个动态角的探究过程,评价教具、评价不同的做角的方法(实质上是评价角的两种生成性定义),强化了对概念的理解,尤其突出角的动态概念,为后面学习判断角、比较角的大小的方法埋下伏笔。】
活动三:创造——判断角
1.活动:试做直角、锐角、钝角。
2.汇报。
生:直角最难摆,先把活动角的一条边、顶点和三角尺的重合,把另一条边旋转到紧贴三角尺,这时的角就是直角。
师:(保持直角造型)哪位同学有疑问?
生:什么地方重合了?
生:先将顶点和一条边重合,再旋转调整另一条边,直至和三角尺上的直角完全重合。这就把三角尺上的直角复制下来了。
师:老师也要做一个直角,需要怎么做?
生:需要借助三角尺。将三角尺的端点和射线的端点、三角尺的一条边与射线分别重合。
师:也就说要点对点,边对边。然后怎么做?
生:将这条射线绕着它的点旋转到三角尺的另一条直角边上。
师:你们说开始我就开始旋转,你们说停我就停下来。
师(绕着射线端点进行旋转):还不停吗?还不停吗?
生:不停,不停。停!
师:为什么这里要我停?你有什么想说的?
生:因为这里不停的话就会大于直角。超出这个位置旋转出的角就是钝角。要是旋转的时候在直角这条边的里面,就会做出锐角。
师:刚才那位同学说“直角最难了”,难就难在直角的位置只有一个,我们只要研究好了直角,锐角和钝角就能迎刃而解了。
【设计意图:高阶思维中的“创造”体现在新颖、自觉地借助数学概念解决问题,学生需追本溯源、有理有据地判断角的类别,同时还需甄别角的两个概念是否可为本环节所用,一条射线绕着端点旋转的程度不同,所形成的角的大小就不同,而直角的判断更需要观察、联想、转化能力等创造性地运用角的动态概念。】
活动四:反思——比大小
1.活动:从这些角中任选两个比大小。
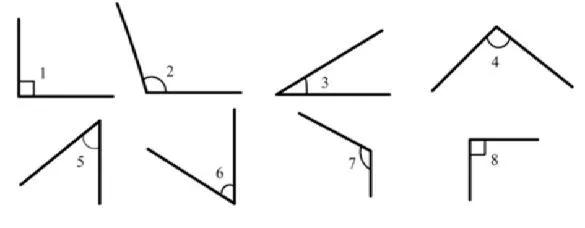
1.直接比较。
师:已经有人一眼就能看出大小了。
根据学生回答小结:钝角>直角>锐角。
2.间接比较。
师:不同类别的角可以一眼看出,可是如果遇到没法一眼比出大小的角,怎么办?请试着选两个,例如两个都是锐角,或者两个都是钝角,再进行比较。
3.汇报。
生:我比较∠1和∠4,用三角尺量的,∠1刚好和三角尺的直角重叠,所以∠1是直角。再用三角尺的直角量∠4,我在∠4的里面画了一条直角的边线,说明∠4大于直角,所以∠4>∠1。
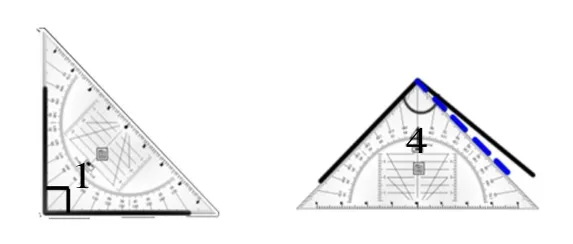
师:这个方法如何?
生:因为∠1刚好是直角,所以可以用这个方法,但如果都是钝角,例如∠4与∠2比,余下的角还是不明显。
师:有道理。那还有别的方法吗?
生:我用之前材料做出的活动角,先量出∠2,然后再放到∠4处进行比较。∠4的两条边都在∠2中,说明∠4<∠2。

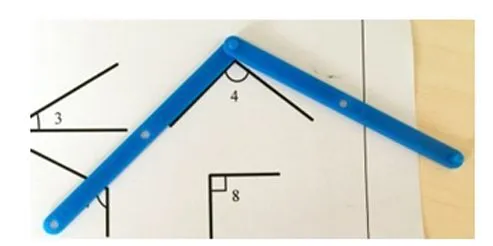
师:像这样的方法叫做“重叠法”。
生:我有一个问题,如果角的大小只差一点点,无法用肉眼比较,活动角也不能精确地比较出来,那怎么办?
师:你在精确度上提出了一个更专业的问题。谁知道怎么办?
生:(举起量角器)可以用有刻度的量角器。
师:太棒了!所以我们以后还会学习量角器的使用。
【设计意图:本活动借助“反思”将角的认识推上一个新的高度。无法直接看出角的大小时,需要借助工具,有的是借助三角尺的直角边,有的借助活动角,有的想到使用量角器,而这三种工具是有递进层次的:在反思现有方法的有局限性时,新工具应运而生,最终量角器的学习水到渠成、顺理成章,而且在量角方法的本质上一脉相承。】
