《三角形的面积》教学设计
2017-04-01冷满红
冷满红
【教学内容】
人教版五年级上册第91~92页。
【教学目标】
1.理解三角形的面积计算与平行四边形的面积计算之间的关系,理解掌握三角形的面积计算公式,并会应用面积公式解决问题。
2.通过观察、操作、想象、对比、讨论等课堂活动,经历三角形面积计算公式的推导过程,掌握转化的方法。
3.体会数学知识是相互联系的,学会用联系的眼光看待数学问题。
【教学重点】
理解掌握三角形的面积计算公式,并会正确应用。
【教学难点】
理解“倍拼”后,原三角形与平行四边形之间的联系与区别。
【教学过程】
一、复习铺垫
师:前面我们已经学习了平行四边形面积的计算。还记得我们是如何推导出平行四边形的面积计算公式的吗?
师:我们将平行四边形通过剪拼,转化成了长方形,利用长方形的面积计算公式推导出了平行四边形的面积计算公式。这就是“化新为旧”。也就是说,我们已学过的知识点中,其实都蕴含着新问题的解决办法。
师:带着这些经验,看到《三角形的面积》这个课题,你想到了哪些旧知识?
【设计理念:通过回顾平行四边形的面积推导过程,激活学生运用转化方法解决问题的经验。对“新”、“旧”的讨论,明确转化的基础与方向。】
二、探究新知
1.猜想。
(1)出示一个底为6厘米,高为4厘米的三角形。
师:看到这个三角形,你想到对应的平行四边形了吗?它在哪儿?
(让想到的学生说一说,到屏幕上指一指。然后在课件上用虚线标示出对应的平行四边形)
【设计理念:将三角形置于等底等高(同底同高)的平行四边形的背景之中,为学生探索三角形与对应的平行四边形之间的关系以及联想、推导三角形的面积计算公式搭建桥梁。】
(2)观察这个三角形与对应的平行四边形,并思考:
①这个三角形与对应的平行四边形有什么关系?
引导学生认识到:
a既是三角形的底,也是对应的平行四边形的底。
h既是三角形的高,也是对应的平行四边形的高。
三角形的面积是对应的平行四边形面积的一半。
(在理解这一点时,可以借助三角形的运动验证拼成平行四边形的两个三角形是否全等,从而帮助学生思考)
这个平行四边形的面积怎样计算,这个三角形的面积呢?
(学生计算,并说一说每一步解决的是什么问题。然后再将计算的过程进行比较)
师:刚才我们探求这个三角形的面积时,这个对应的平行四边形可是帮了大忙了。如果所有的三角形,都能找到这样对应的平行四边形,那么求它们的面积只要怎么做就可以了?
【设计理念:将三角形与对应的平行四边形进行对比,明确“等底等高(同底同高)”的三角形与平行四边形之间的联系与区别,并初步探索出三角形的面积计算公式,为后续验证指出明确的方向,奠定坚实的基础。】
2.探究。
(1)自由探索。
师:是不是所有的三角形都可以找到一个与之对应(同底同高)的平行四边形呢?从作业纸中选择一份,试一试。
作业纸1:空白方格图。要求:在点子图上任意画一个三角形,再画一个三角形和它组成平行四边形。
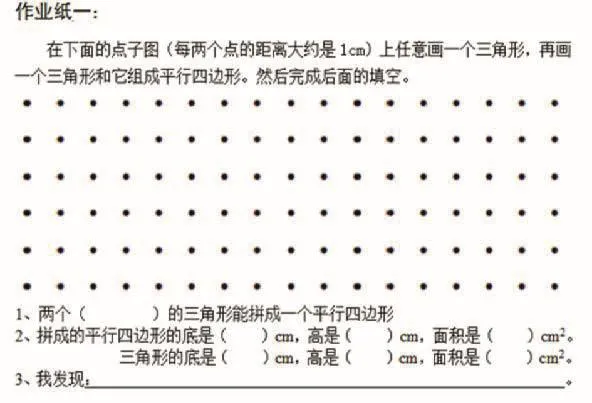
作业纸2:已画有一个三角形的点子图。要求:在学具袋的三角形中选择一个和点子图中的三角形拼成平行四边形(贴到点子图上)。
作业纸3:在学具袋的三角形中,选择两个三角形,拼成平行四边形。然后贴到点子图上。
出示活动要求:
①选择一份作业纸并完成。
②和同桌说一说你的发现。
(学生操作后展示交流)
【设计理念:让学生自由探索,寻找与一个给定的三角形对应(同底同高)的平行四边形,一方面让学生感知、体会这两个图形之间的联系;另一方面在画图等操作与讨论中,发展学生的空间想象能力。在探索中,以点子图为背景,使“度量”因素贯穿操作的始终,方便学生从“数”的角度思考图形以及图形之间的关系。】
(2)分类探索。
师:刚才我们为多个三角形找到了等底等高的平行四边形。那么是不是所有的三角形,都能找到与它等底等高的平行四边形呢?
师:三角形有无数个,一个一个验证行得通吗?想一想,可以怎样做?
[在点子纸上出示(等底等高的)直角三角形、锐角三角形、钝角三角形]
师:你能找出与这些三角形等底等高的平行四边形吗?它们的底和高分别是多少?
师:你会计算它们的面积吗?说一说列式的根据是什么?
师:这些三角形的形状各不相同,它们的面积相等吗?为什么?
【设计理念:从自由探索走向分类探索,培养学生思维的条理性,感受数学的严谨性。在验证中,进一步体会感悟对应的三角形和平行四边形之间的联系:等底等高。而这正是推理总结出计算公式的基础。同时,通过观察发现三种不同形状但等底等高的三角形面积相等规律,引导学生感悟三角形的面积与底、高之间的关系。】
3.小结。
师:三角形的面积公式我们现在可以确定吗?这里的a、h的积表示什么?为什么要除以2?
【设计理念:无论是对公式的解读,还是在解决问题中应用,教师引导学生反复追问ah的含义,旨在梳理学生的思维脉络,从而深入理解三角形的面积计算公式。】
三、课堂练习
1.基本练习。
如图,三角形的底是100cm,高33cm,它的面积是多少平方厘米?

师:你从中知道了哪些数学信息?底是100厘米,高是33厘米,说的是什么图形的底和高?你找到对应的平行四边形了吗?
(学生利用公式计算后全班交流)
师:这里的100×33的积表示的是哪个图形的面积?为什么还要除以2?
小结:要求三角形的面积,先求平行四边形的面积。
2.变式练习:求三角形DBC的面积。

3.拓展练习。
下图平行四边形底边的中点是A,它的面积是48平方米。求涂色的三角形的面积。

【设计理念:在练习中,巩固学生对三角形和对应的平行四边形的联系,以及对三角形面积计算公式含义的理解。在课堂上,为方便学生探索,研究的“等底等高”其实都是“同底同高”,设计变式练习与拓展练习,旨在丰富学习素材,让学生体会到等底等高的更广阔的外延,从而避免思维的僵化。】
四、全课小结
师:这节课,你有什么收获?
五、数学欣赏
1.三角形转化成长方形的两种方法。
2.《九章算术》中的三角形面积计算。
附:板书设计:

