《钉子板上的多边形》教学

王学红

【教学内容】

苏教版第九册第108～109页《钉子板上的多边形》。

【教学过程】

一、回顾旧知，激活经验

谈话：同学们，我们已经学会了一些图形的面积计算。这些多边形的面积你会计算吗？需要知道哪些条件？

出示：

师：看来计算多边形面积要知道边的长度。

计算：（补充数据）学生口答多边形的面积。

【设计意图：课始通过出示这4个多边形，唤醒学生研究多边形面积的经验。通过补充边的长度并计算面积，不仅回顾了计算多边形面积的常用方法，更重要的是引领学生发现常用的方法都是通过“边的长度”这一途径的。】

二、另辟蹊径，探索规律

1.明确探索路径。

激疑：换个角度，不通过边的长度来计算多边形的面积，是否还有别的方法呢？

播放微视频，介绍皮克定理：1899年，奥地利的数学家皮克发现了计算多边形面积的另一条路径。他将多边形放到格点中研究，发现多边形面积与多边形边上钉子数、边内钉子数之间的规律，并进行了证明。这个规律被称为“皮克定理”，被誉为史上“最重要的100个定理”之一。

揭题：多边形面积与多边形边上钉子数、边内钉子数到底有什么关系呢？今天这节课就让我们共同来探索这其中的奥秘吧！（板书：边内钉子数、边上钉子数、多边形面积）

2.自主探索内部只有1枚钉子的多边形。

（1）观察猜想。

师：（在原来的图形下出现钉子板）还以刚才的4个图形为例，换个角度思考，你能从中发现什么？独立完成1号研究单。

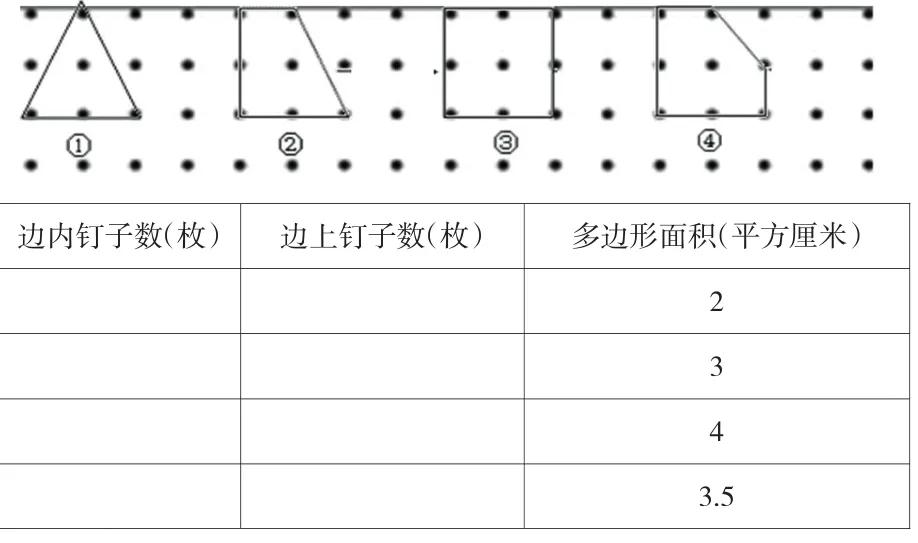
我发现：（）

（2）自主验证。

师：这个发现对不对呢？怎么办？自己再举几个这样的例子验证验证！为了研究的方便，我们把钉子板换成点子图。请同学们在点子图中再画几个这样的多边形，数一数，算一算。

（学生验证交流）

预设一：学生画出的是边内只有1枚钉子的图形，验证成立。

预设二：学生画出的图形不符合规律，验证不了。

观察比较：（对比两种情况）这是为什么呢？

完善规律：边内只有1枚钉子时，多边形面积等于边上钉子数除以2。

（3）符号表达。

师：如果用S表示多边形的面积，n表示多边形边上的钉子数，这个规律可以用字母怎么表达？用字母表达感觉怎么样？

3.分组探究内部有0枚、2枚、3枚、4枚……情况。

过渡：多边形内不是1枚钉子又会有什么规律呢？想试一试吗？小组商量一下，你们想研究哪种情况？

（1）小组合作，探索规律。（完成2号研究单）

合作要求：①画一画：每人画一个内有（）枚钉子的多边形。

②填一填：算出多边形面积，数出边上钉子数，完成表格。

③说一说：观察分析，你能从中发现什么共同之处？

④试一试：再举几个例子试一试，是否符合这一规律？

边上钉子数（枚）　多边形面积（平方厘米）边内有（）枚钉子。2　3　4 3.5

我发现：（）

（2）大组交流，合成规律。

师：要让自己变聪明，首先，我们要学会由一个想到许多个。例如我们由内部只有1枚钉子，想到了0枚、2枚、3枚、4枚……我们还要学会把许多个变成一个。

（学生分组汇报的过程中比较）这些看似不同的规律之间有联系吗？

边内的钉子数（枚）　边上钉子数（枚）　多边形面积（平方厘米）0 n S=n÷2-1 1 n S=n÷2 2 n S=n÷2+1 3 S=n÷2+2 4 n S=n÷2+3 a n n

师：“换个角度，就有新路”。要求多边形的面积，现在我们又多了一个途径。只要知道——？如果用a表示边内的钉子数，这个多边形面积S可以怎么表示？

4.应用规律，体会价值。

运用格点法计算海安七星湖的占地面积，体会其实际应用的价值。

【设计意图：上述四个活动，是本课的“重头戏”，围绕三个问题展开教学：“多边形面积计算的另一条路径在哪里?”“这条路径是什么？”“这一规律有什么用？”由简单到复杂，由一般到概括，环环相扣，螺旋上升，让学生在智力冲浪中发展规律。当然，作为探索规律的活动，注重的不仅是结论的得出，更重要的是过程的经历，经验的积累，以及“观察比较——猜想验证——得出结论”的科学研究方法的感悟。】

三、总结提炼，深化理解

提问：回顾本课探索和发现规律的过程，你有哪些收获？

小结：通过今天的学习，我们知道多边形面积的计算不仅可以通过边的长度来计算，还可以通过边内、边上的钉子数来计算。这两种方法之间其实是相通的。将来同学们学的数学知识越来越多，就会明白其中的道理了。

四、拓展延伸，升华主题

【设计意图：学生在课堂中运用不完全归纳法探索出规律，为研究多边形面积又打开了一条新的路径。从这一角度看，本课的学习价值更加重在对学生进行思维拓展启迪，用八个字来概括，就是“换个思路，就有新路”。课尾微视频的播放，让学生回顾不仅在形的世界里，在数的世界里也有这样的例子。从而让学生真正感受的“换个角度，就有新路”的神奇魅力！综观整节课的教学，力求让学生在规律之外感受到探索过程中获得的方法，及其规律背后蕴含的思想价值。】