基于Lorenz三维系统的伪随机二值序列生成方法

刘 冰，刘雪梅(1. 达州职业技术学院，四川达州65001；2. 西南大学计算机与信息科学学院，重庆北碚400715；. 四川省达州市统计局，四川达州65000)

基于Lorenz三维系统的伪随机二值序列生成方法

刘 冰1,2，刘雪梅3
(1. 达州职业技术学院，四川达州635001；2. 西南大学计算机与信息科学学院，重庆北碚400715；3. 四川省达州市统计局，四川达州635000)

针对目前大多数伪随机二值序列的生成方法皆不能很好地满足Golomb的三个随机性假设,提出了一种基于三维Lorenz混沌系统的伪随机二值序列的生成方法.首先通过三维Lorenz混沌系统生成三个离散随机序列，然后在这三个序列中分别取较小的序列数轮次地组成新的序列并转换成二值序列.通过大量反复的检验，生成的二值序列中任意较大长度的序列皆能通过频数检验和序列检验，其相关性和随机性表现也都达到了较为满意的效果.

Lorenz系统；混沌映射；二值序列；频数检验；序列检验

0 引言

信息技术的发展及互联网的普及一方面给人们带来了巨大的便利，另一方面，也因为信息在存储、传输等方面存在的不安全问题带来诸多困扰.如何保证信息在存储、传输和获取等诸多环节上能够安全、完整和可用已成为当前信息技术领域的研究热点之一.在我国，信息安全正成为国家安全的一个重要方面，随着信息技术的快速发展及互联网的普及应用，如何更有效地保障信息的安全正越来越成为人们急需要解决的问题.

目前，解决信息安全问题的一个重要方面是对信息的存储、传输及识别进行加密处理.[1]随着信息技术的发展与进步，各种加密技术不断涌现.在众多的加密方法中，伪随机二值序列的加密方法由于其实现简单、执行速度快、传播错误少、安全性高等特点，[2-4]它常被应用于国防、军事、外交等许多重要的领域.但由于目前大多数方法所生成的伪随机二值序列皆不能很好地满足Golomb的三个随机性假设，[5-7]因此，如何生成性能良好的伪随机序列，也就成为该类加密方法中的一个重要的研究课题.

自从1989年英国数学家Matthews提出基于混沌的加密思想以来，[8]越来越多的学者通过引入混沌系统来生成二值序列取得了不错的效果.[9-12]本文将以Lorenz三维混沌系统为基础，提出一种伪随机二值序列的生成方法，并对其相关性能做深入分析.

1 相关概念

定义1 如果一个序列中可取的值只有0或1，且该序列能够预先被确定、重复地生成和复制，同时，又具有某种随机特性，则称此序列为伪随机二值序列.

评价其随机特性的主要指标一般包括：平衡性、游程性和相关性等.其具体定义如下：

定义2 设s={s0,s1,…,sN-1}(N∈Z)是周期为N的二值序列(si=0,1),记为：Nk=|{i|si=k,k∈Z2,i∈[0,N-1]z}|.

(1)

若在序列s的一个周期内满足:|N0-N1|1.则称二值序列s具有平衡性.其中，周期N是指序列s的最小正周期.

定义3 设s={s0,s1,…,sN-1}(N∈Z)是周期为N的二元序列(si=0,1)，将它的一个周期段s0,s1,…,sN-1依次排成一个圆周，并使首尾相邻，即s0与sN-1相邻.则称圆周上蝉联在一起的1(或0)为1(或0)的游程.一个游程中蝉联在一起的1(或0)的个数叫做游程的长度.

如果序列在一个周期内满足：(1)长度为1的游程占游程总数的1/2；(2)长度为l(l≥2)的游程占游程总数的1/2l；(3)在同样长度的所有游程中，1的游程和0的游程大约各占一半.则称该序列具有伪随机序列的游程特性.

则称序列s具有理想自相关.

2 伪随机二值序列生成方法

2.1 三维Lorenz混沌系统

Lorenz系统是经典的三维混沌系统，与较低维的混沌系统相比，其结构更复杂、密钥空间更大.其动力学方程如公式(3)所示：

式(1)中，a,b,c为系统参数，典型的值为a=-8/3，b=-10，c=28，在保持a,b不变，c>24.74时Lorenz系统进入混沌状态.

2.2 伪随机二值序列的生成

本文运用四阶R-K方法对公式(3)进行求解.在本文中，设步长：δ=0.0005，初值：x=0.8436001，y=1.324562，z=0.683571.得到的三个离散混沌序列分别记为：x0,x1,x2,…,xn；y1,y1,y2,…,yn；z0,z1,z2,…,zn.其中n为序列长度.

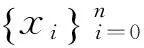
设序列X的最小值、最大值分别为min(X) 、max(X)，取p0∈(min(X) , max(X)),令ε为一较小正数.构成如下集合U0：

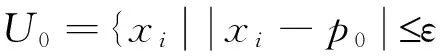
(4)

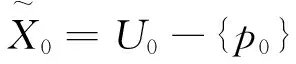
h3η≥2ε/δ, 其中δ

构成如下集合U1：

(6)

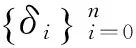
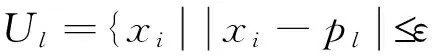
(7)

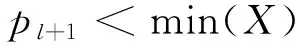
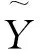
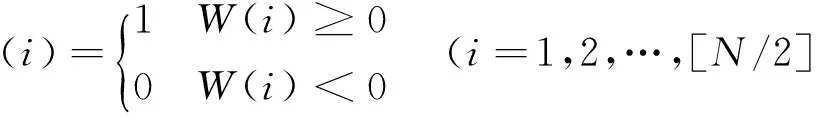
(8)

其中N为W序列的长度，表示取整数运算.

3 性能分析方法与检验结果

3.1 二值序列性能分析方法

为了验证第2节提出的方法的可行性，下面将分别对其生成的序列进行频数检验、序列检验和相关特性测试.

(1)频数检验: 通过计算随机二值序列中0和1的出现频数来反应该序列的置乱状况，若大致相等，则说明该序列达到置乱效果.令n表示二值序列0和1的总个数，n0为二值序列中0的总个数，n1为二值序列中1 的总个数.则下式近似服从自由度为1的卡方分布：

若式(9)得到的值小于其5%显著水平对应的值3.84时，则说明该序列通过频数检验.

(2)序列检验: 通过计算随机二值序列中的任意位序的0(或1)之后出现0(或1)的概率，来反应该序列的置乱状况，若大致相等，则说明达到了置乱效果.令n00表示二值序列中00的总个数，n01表示二值序列中01的总个数，n10表示二值序列中10的总个数，n11表示二值序列中11的总个数.则下式近似服从自由度为2的卡方分布：

若式(10)得到的值小于其5%显著水平对应的值5.991时，则说明该序列通过检验.

(3)相关特性: 设A,B为两个混沌二值序列，k为整数.如果下式(11)中的函数r(k)满足：r(0)→0.5和r(k)→0(k≠0)，函数p(k)满足：p(k)→0，则序列通过检验.

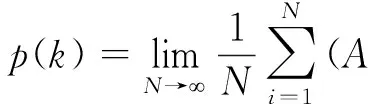
(11)

其中：r(k)描述是序列的自相关性，p(k)描述的是序列的互相关性.

3.2 随机性检验结果

本节运用3.1节提出的方法对第2节所产生的混沌二值序列进行多次重复试验，得到较为理想的的结果.在试验中，仍然选用第2节的初值x=0.8436001，y=1.324562，z=0.683571来生成一个混沌随机二值序列，从该序列中的任意位置处开始截取一个较长长度的序列(比如10000以上)来进行检验，其频数和序列检验的结果均100%的通过.表1显示为一个随机抽取的二值序列，从中截取104～105项不等的试验结果.

表1 二值序列随机性能分析结果

随机抽取的两个混沌二值序列自相关函数图和互相关函数数分别如图2的(a)、(b)所示，(a)图显示，r(k)→0(k≠0)，r(0)→0.5，(b)图显示p(k)→0，由此说明运用本文提出的算法所产生的序列达到了理想的混沌效果.

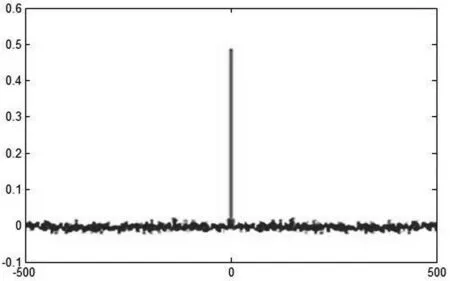
(a) 自相关函数

(b)互相关函数

同时，运用本文提出的方法在产生序列时，表现出了极高的敏感性.当对初始值给予微小的改变，都会引起该序列的后续值发生显著的变化.在本文的测试中，我们取x=0.8436001+10-10，其余值不变来进行测试，显然该值仅较原来的初值增加了10-10，从下表(2)中不难发现所产生的序列中仍有近50%的位发生变化，可见其序列的产生对于初值的变化具有极高的敏感性.

表2 初值敏感性实验

4 结论

本文针对目前大多数伪随机二值序列生成方法不能很好地满足Golomb随机性假设，提出了一种基于Lorenz三维混沌映射的伪随机二值序列的生成方法.首先通过混沌系统生成三个用于原始的离散随机序列和一个用于改变步长的离散随机序列，然后在这三个原始序列中分别取满足一定条件的较小的序列数轮次地组成新的序列并将其转换成二值序列.通过大量反复的检验，生成的二值序列中任意较大长度的序列皆能通过频数检验和序列检验，其相关性和随机性表现也都达到了较为理想的效果.由于伪随机二值序列的加密方法应用领域较广，因此，本文提出的方法应具有一定的市场价值.

[1]ShannonC.E.Communicationtheoryofsecretsystems[J]. Bell system technical journal，1949(4):656-715.

[2] 张雪锋．混沌序列生成技术及其若干应用研究[D]. 西安:西安电子科技大学，2011:1-22.

[3] 李小平．伪随机序列的构造及其性质分析[D].西安：西安电子科技大学，2014:1-19.

[4] 李红燕,杨万利．时空混沌二值化方法研究[J].计算机工程与应用,2013(21)：65-69.

[5] 王云峰，沈海斌,等．输出一密文混合反馈混沌流密码的设计[J].浙江大学学报:工学版，2006(11):1972-1975.

[6] 詹 明，张翠芳．一种基于混沌控制m序列的密钥序列生成方案[J]．电子与信息学报，2006(12):2351-2354.

[7] Golomb S W.Sequenceswithrandomnessproperties[M].Baltimore:Terminal progress, 1955:10.

[8] Matthews R.Onthederivationofachaoticencryptionalgorithm[J].Crytologia, 1989(13):29-42.

[9] Narendra Singh, Aloka Sinha.OpicalimageencryptionusingHartleytransformandLogisticmap[J]. Optics Communications，2009(2):1104-1109.

[10]MarcelAusloos, Miche Dirickx.Thelogisticmapandtheroutetochaos[M]. Berlin：Springer-Verlag, 2006：18.

[11]余振标，冯久超．一种混沌扩频序列的产生方法及其优选算法[J]．物理学报，2008(3):1409-1415.

[12]罗启彬，张 健．一种新的混沌伪随机序列生成方式[J]．电子与信息学报，2006(7):1262-1265.

[责任编辑 范 藻]

PseudorandomBinary Sequence Generation Method Based on Lorenz 3D system

LIU Bing1,2, LIU Xuemei3

(1. Dazhou Vocational and Technical College, Sichuan Dazhou 635001;2. Computer and Information Science College of Southwest University, Chongqing 400715; 3. Statistics Bureau of Dazhou City,Dazhou Sichuan 635000, China)

In this paper, a method of generating pseudorandom binary sequences based on 3D Lorenz chaotic system is proposed, which can not satisfy the three stochastic assumptions of Golomb. First, three discrete random sequences are generated by the chaotic system, and then the new sequences are transformed into binary sequences by taking smaller sequence numbers in the three sequences. Through a large number of repeated tests to generate binary sequences of any larger length of the sequence can pass the frequency test and sequence test, the correlation and random performance also reached a satisfactory effect.

Lorenz system; chaotic mapping; binary sequence; frequency test; sequence test

2016-12-28

四川省教育厅重点科技计划项目(14ZA0330)；四川省达州市2014年科技计划项目(2014-8220)

刘 冰(1970—)，男，四川达州人.副教授，主要从事信息安全与图像处理研究.

TP309

A

1674-5248(2017)02-0033-04