基于并行优化与访存优化遗传算法的TSP问题求解方法

陆 游,何 嘉(成都信息工程大学计算机学院，成都610025)

基于并行优化与访存优化遗传算法的TSP问题求解方法

陆 游,何 嘉
(成都信息工程大学计算机学院，成都610025)

TSP(旅行商问题)问题是数图论领域中著名问题之一，常采用基于种群的智能算法来解决，其中最具代表性的就是遗传算法.但由于用遗传算法在解决TSP问题时往往比较耗时，并且随着TSP问题规模的增大，时间的消耗也大大增加，因此采用了并行优化与访存优化方法对遗传算法进行了从代码层面的优化，从而提高TSP问题的求解效率.最后，通过实验验证了该加速方法的可行性.

遗传算法;TSP问题;并行;访存

TSP问题(Traveling Salesman Problem)，简称旅行商问题)是一个典型的NP难题，随着智能方法的流行，使其能够在相对较短时间内求得近似解，虽然这些算法不能得到精确解，但其误差能够控制在可以接收的范围内.大量的科学实验证明以基于种群的一些智能算法(遗传算法，蚁群算法等)在求解TSP问题上具有较高的寻优能力，[1]但随着问题规模和迭代次数的增加，程序的运行时间依然会大大增加，甚至短时间内无法得到结果.因此，为了能更快地得到结果，本文采用了并行优化和访存优化两种方法对程序进行了代码层面的加速，以期望最大限度地缩短程序的运行时间.由于在这类基于种群的算法中，遗传算法是其最经典，最具有代表性的算法，因此选用标准遗传算法作为研究对象，提出了基于并行优化与访存优化的遗传算法的TSP问题求解方法.

1 遗传算法

1.1 遗传算法简介

遗传算法(Genetic Algorithm，简称GA)是模拟达尔文论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法.它于1975年由美国的Holland教授在他的专著《自然界和人工系统的适应性》中首先提出.[2]遗传算法，其描述如下：

(1) 初始化.确定种群规模N、最大进化迭代次数T、交叉概率P_CROSS、变异概率P_MUTATION、产生N个随机数将其编码后作为算法的初代种群.

(2) 适应度评价.对种群每一个个体好坏的评判标准，一般来说，个体越好，其适应度值越大，越容易被遗传.

(3) 选择运算.将选择算子作用于群体.目的是选择优秀个体即适应度值较大的个体进行遗传操作.

(4) 交叉运算.将交叉算子作用于群体.将选出来的个体依照交叉概率PC进行两两交叉.

(5) 变异运算.将变异算子作用于群体.对群体中的个体串中的某些位依照变异概率PM进行改变.

(6) 种群经过以上一系列操作后得到下一代群体.

(7) 终止条件判断.若达到最大迭代次数，则输出结果；未达到最大迭代次数，返回步骤(2).

1.2 遗传算法的并行优化

由于遗传算法的天然并行性，因此本文采用了基于共享内存的OpenMP(Open Multi-Processing) 并行技术对其进行了并行优化.[3]

在遗传算法中，计算每个个体适应度值、选择操作、交叉操作、变异操作中内部的数据相互独立，所以这几部分非常适合用共享内存的多核CPU做细粒度的并行.如图1所示，本文将适应度评价、选择、交叉、变异这四部分操作都分成了n个线程来并行地执行.

1.3 遗传算法的访存优化

在过去二十几年中，虽然处理器速度与存储器的速度都有大幅的提高，但两者之间的增长速度仍有不小差距.[4]到目前为止，处理器的速度仍然远远高于存储器的速度，所以在当前的计算机体系结构中往往都会在CPU与内存之间引入高速缓存(Cache)，由图2可知，CPU首先会从Cache中取数据，如果没有找到则才再从内存中取数据.由于Cache的存取速度远高于内存(Cache的存取速度接近于CPU)，因此如果能让CPU每次访问数据的时候尽可能的都能在Cache中找到，那么程序的运行效率将会大大提升.

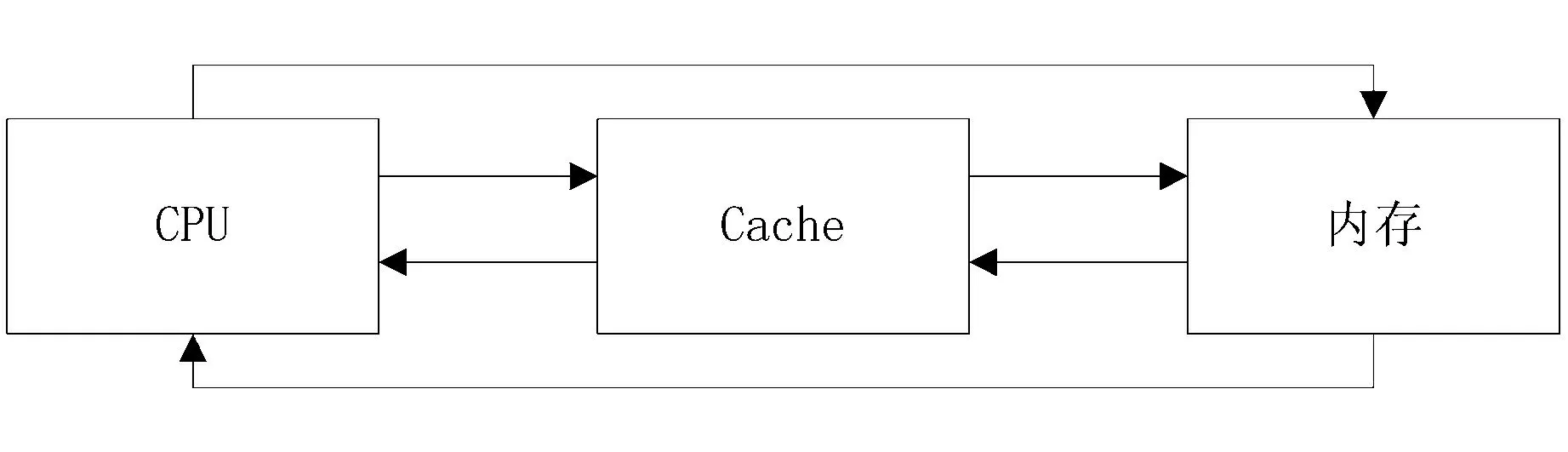
图1 Cache系统工作原理图

因此，本文将采用此原理来适当调整访问数据的顺序来尽可能多地让每一次需要数据能在Cache中被访问到.经多次实验发现，本文的遗传算法所采用的轮盘赌选择算子在每一次迭代的时候，适应度大的个体更容易被选择到，但这些适应度大的个体数据又很有可能不在Cache中.因此本文的思路就是在每一次迭代的适应度评价后，将个体按照适应度从大到小排序，又因为Cache访问内存是按照内存的地址顺序访问，因此在个体排序后，适应度大的个体将会优先存放在Cache中.

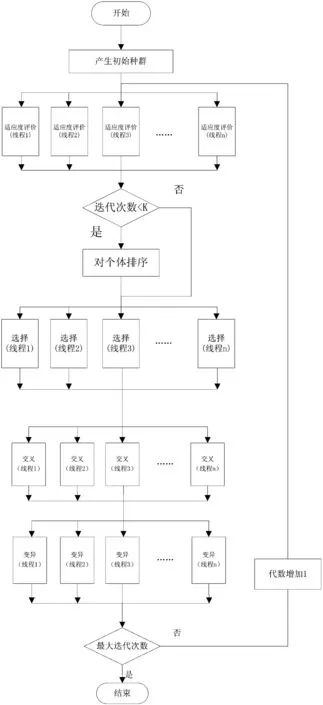
图2 访存优化遗传算法原理

如图3所示，假如按照此思路调整了个体存放顺序后，适应度大的个体优先被Cache所缓存，假如就是个体1，2，3，4.当进行轮盘赌选择算子时候，概率越大的个体则有更大的几率被CPU选中，也即CPU会有更大的几率在Cache中找到数据，这样依次类推，Cache每次都会缓存CPU最有可能访问到的数据.因此，经过访存优化后的遗传算法则会有更高的运行效率.

根据遗传算法的原理，随着代数的增加，种群的多样性会逐渐变小，也即到了遗传算法后期，每个个体与上次迭代的时候变化不大，而又由于每次迭代时候的排序会消耗一定的时间，因此本文设置了一个K值，当迭代次数小于K就执行排序，大于K时就不执行排序.这样能使其优化效率最大化.

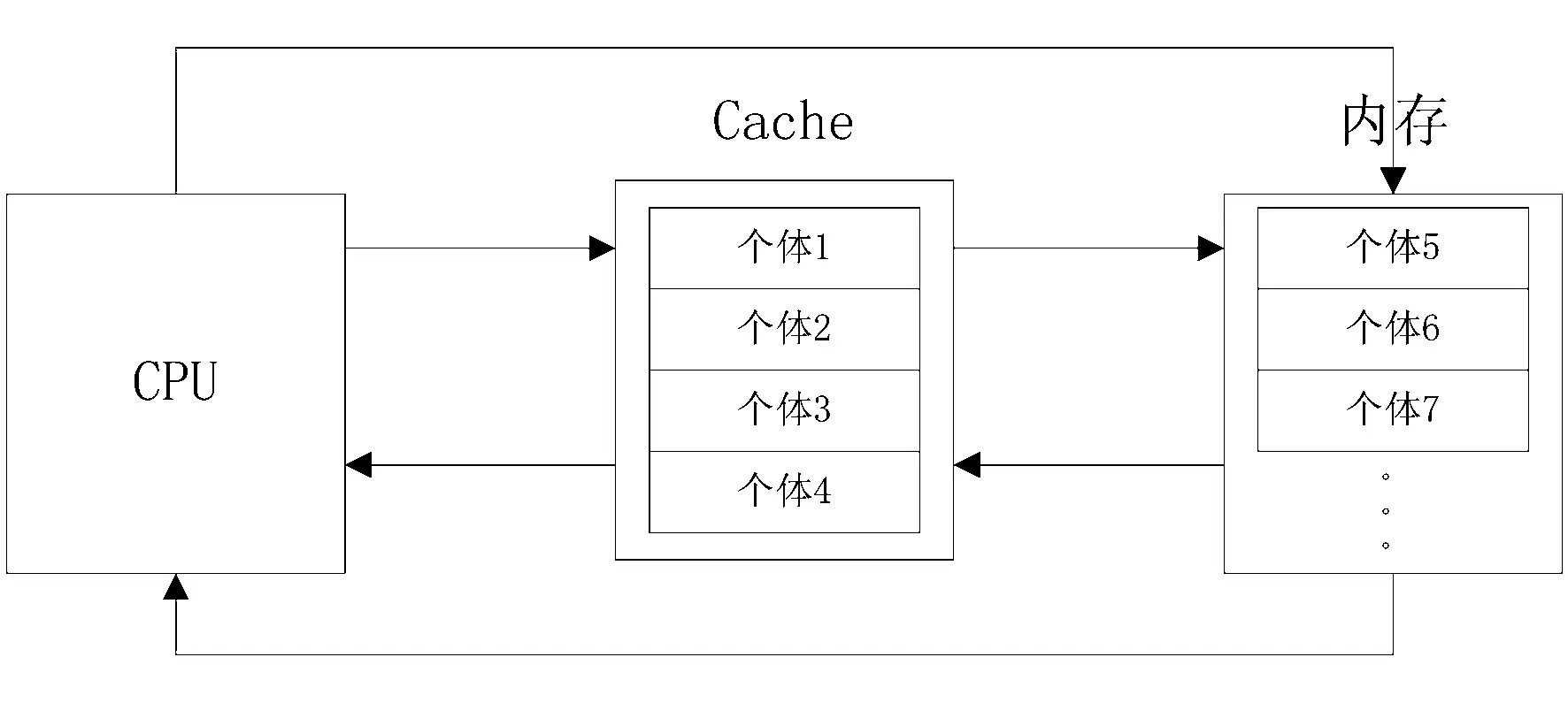
图3 优化后的遗传算法框架图

2 优化后的遗传算法求解TSP问题

2.1 TSP问题

TSP问题是数图论领域中著名问题之一.该问题的经典提法是：假设有一个旅行商人要拜访n个城市，从城市1出发，经其余各城市至少一次，然后回到城市1，求其最小的路径成本.[5]

TSP问题属于组合优化问题，而遗传算法是一种求解问题的高效全局搜索方法，能够解决复杂的全局优化问题，所以非常适合用来解决TSP问题.[6]该问题已经被证明具有NP计算复杂性，所以很难得到精确解，而遗传算法就是解决这类问题比较有效的近似算法.[7]图4显示了以两条路径A=(1 2 3 4 5 6 7 8)，B=(2 4 6 8 7 5 3 1)为例的标准遗传算法操作式例.[3]

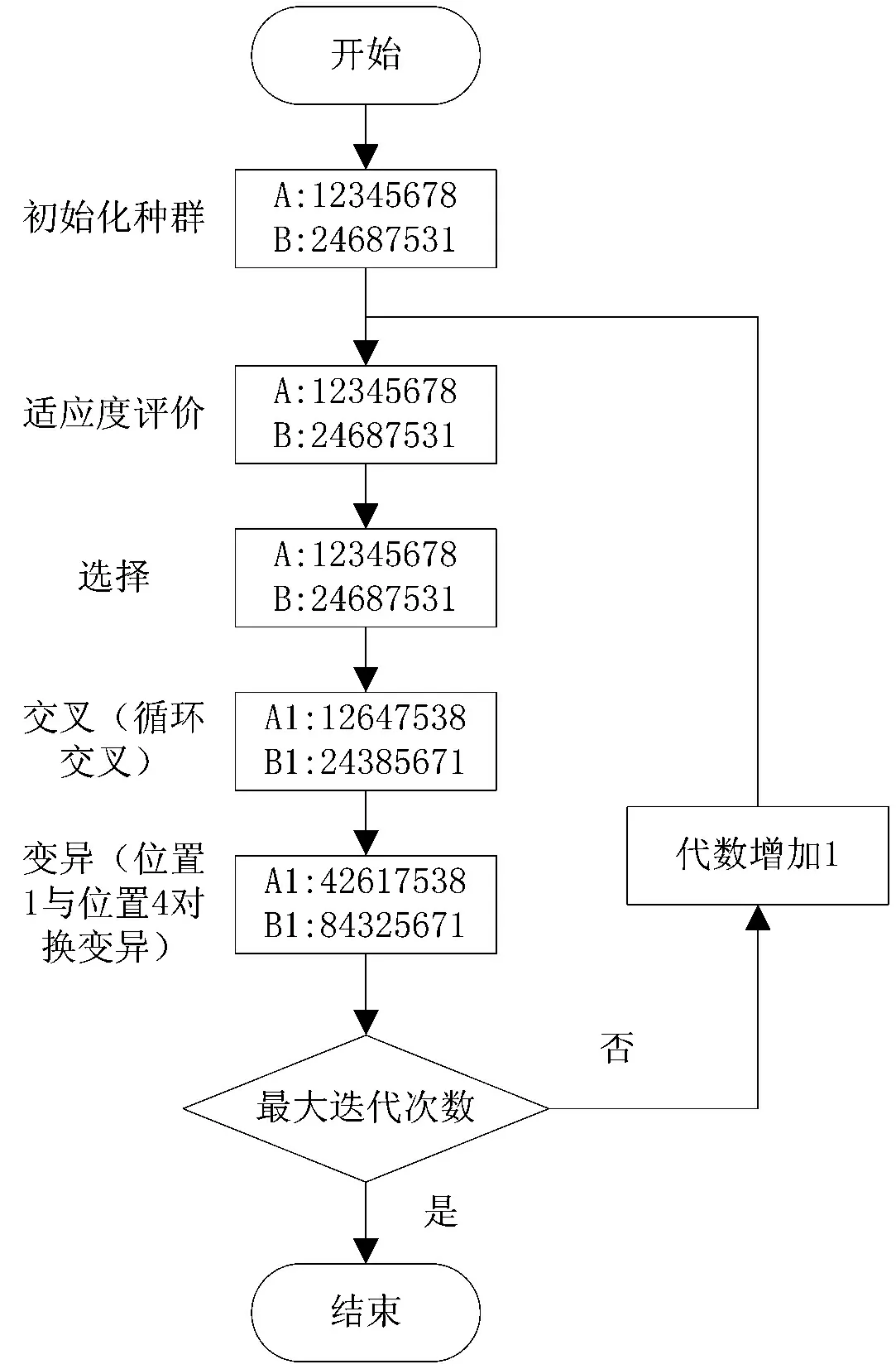
图4 标准遗传算法解决TSP问题操作示例

根据大量实验结果表明，采用遗传算法解决的TSP问题随着城市规模的增大，其程序运行时间大量增加，因此本文就采用优化后的遗传算法来缩短其运行的时间.

2.2 算法描述

2.2.1 编码

在遗传算法求解TSP问题中，目前的编码方式主要有：近邻表示(adjacency representation)、[8]次序表示(ordinal representation)、[9]路径表示(path representation)、[10]布尔矩阵表示.本文采用的是路径表示方式，这是针对TSP问题最自然、最直观的表示方式.

例如：有一条路径为2-3-1-9-4-6-7-8-5可将其表示成(2 3 1 9 4 6 7 8 5).

2.2.2 适应度评价

由于TSP问题解的要求是路径长度越短越好，因此本文的适应度函数取路径长度的倒数：

由于种群内的每个个体计算适应度值是相互独立的，所以本文用OpenMP将这部分并行化，其伪代码如表1所示：

表1 适应度值部分并行伪代码

其中SIZE表示种群大小，CITY_NUM表示城市规模，在OpenMP中用parallel for进行编译指导来优化for循环.为了便于统一和对比，本文采用的都是静态调度的策略(在代码中由schedule(static)体现)，即假如任务量为N，有t个线程，则每个线程分配的任务量为N/t.

2.2.3 排序

在计算完适应度值之后，为了进行如图4中的访存优化，对个体按照其适应度值的大小进行了升序排序，其伪代码如表2所示：

在表2中，T_NOW表示当前迭代次数，K值为多次反复实验得出的值.

表2 访存优化部分伪代码

2.2.3 选择

本文选用遗传算法中最常用的轮盘赌选择，即各个个体的选择概率与其适应度值成比例，适应度值越大的个体被选择的几率也就越大.同样选择操作部分可以并行地选择，因此再用OpenMP将其并行化，伪代码如表2所示：

表3 选择部分并行伪代码

在上述伪代码中，用OpenMP并行化后，编译器默认的是将循环体里的i这个循环变量共享化，即可以让多个线程同时访问i这一变量，若这样将会造成进程间数据的相互影响，从而导致结果的错误.因此，需要语句里加上private这一修饰，将i变为私有变量，即每个线程都有i这一变量的副本，保证每个进程间的数据互不影响.

2.2.4 交叉

针对TSP问题的遗传算法的交叉算子最常用的是基于路径表示的部分匹配交叉(PMX)、顺序交叉(OX)、循环交叉(CX)、边重组交叉、贪心交叉(GSX)等.[6-8]本文选择的是循环交叉的方法.其一般性描述为：

(1) 设有两个父代：

A=(a1,a2,a3,a4 … an)

B=(b1,b2,b3,b4 … bn)

(2)从父代A的左起第一个元素开始作为第一个城市a1，加入到子代A1中：

A1=(a1 … )

(3) 查看父代B中选定的元素a1对应元素，为b1，假如b1=a2，所以得到：

A1=(a1,a2 … )

(4) 查看父代B中选定的元素a2对应元素，为b2，假如b2=a4，，所以得到：

A1=(a1,a2 … ,a4 … )

以此类推，直到检查父代B中所选元素对应的元素已经存在于A中，则循环结束.再将剩余的元素从父代B中填入，得到最终的子代A1.

同样，在这部分两两个体进行交叉相互之间互不影响，故本文再将其用OpenMP进行并行化，伪代码如表3所示：

在表4的伪代码中，P_CORSS表示预先设定的交叉概率，同样在用OpenMP并行化的时候采用的静态调度.

表4 交叉部分并行伪代码

2.2.5 变异

基于TSP的变异算子主要有：点位变异、逆转变异、对换变异、插入变异、贪心对换变异、倒位变异[3,9,10].我们采用的是对换变异，即随机选择串的两点，交换其值.同样，两两个体变异之间互不影响，于是将这一部分再用OpenMP将其并行化，伪代码如表4所示.在表4的伪代码中P_MUTATION表示预先设定的变异概率.

表5 变异部分并行伪代码

3 实验结果与分析

3.1 实验环境

我们所采用的实验环境为：四核Intel(R) Core(TM) i5-4590s CPU 3.00GHz、8GB内存、Windows7操作系统、Visual Studio 2010编译器.为了达到实验效果，本文分别选用了三个数据集来测试，分别是st70、lin318、pr1002，分别代表小规模的TSP问题，中等规模的TSP问题和大规模的TSP问题.为了便于对比，本文的算法参数统一设置如表5所示：

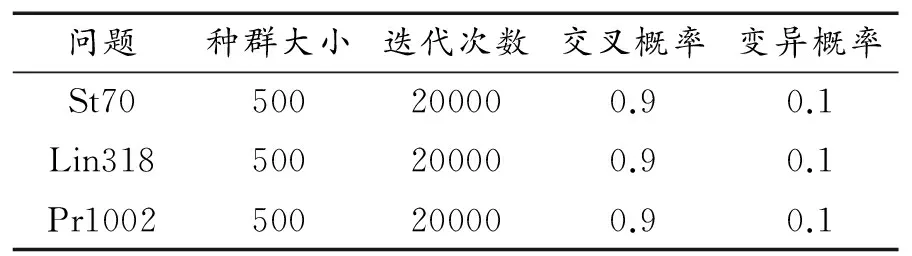
表6 算法参数设置

3.2 并行优化运行时间对比与分析

为方便比较，本文先单独做了并行优化.在实验中我们每隔200代记录了一次当前的运行时间，并分别画出了其变化曲线，如图4、图5、图6所示，其数据为测试20次的平均值.

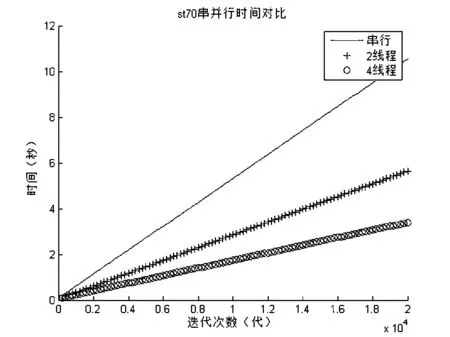
图5 st70串并行时间对比

从图5、图6、图7中可以看出，当迭代次数一定的时候，采用OpenMP并行化后的时间消耗明显少于串行，并且4线程的时间也明显优于2线程.表6为具体的统计数据.

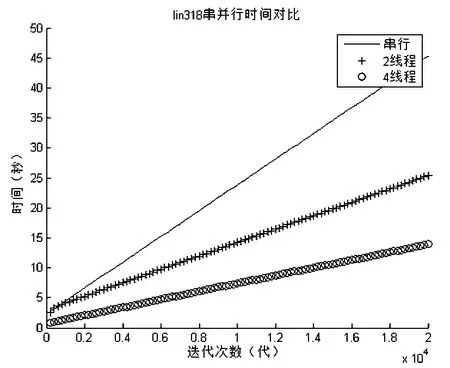
图6 lin318串并行时间对比

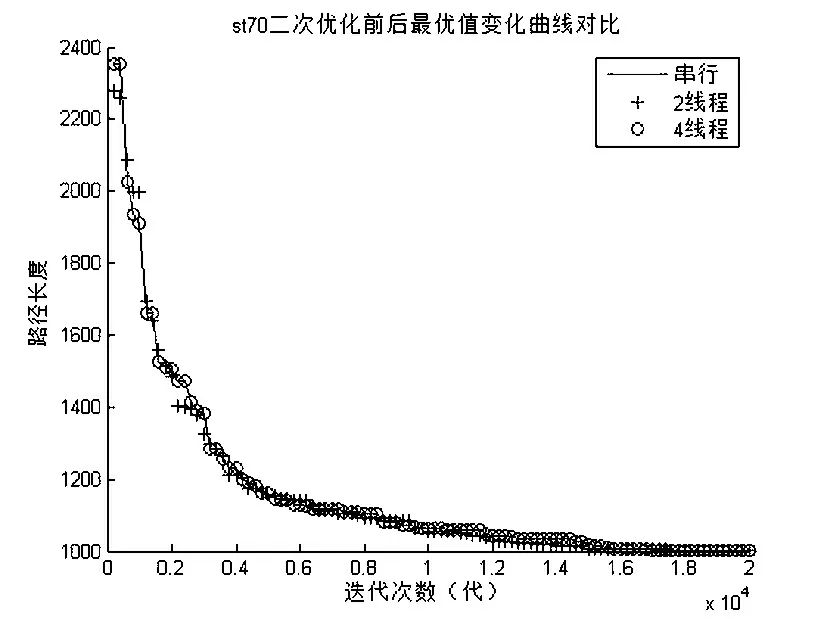
图7 pr1002串并行时间对比

表7为只采用并行优化运行时间统计表，从中可以看出，采用OpenMP后都有明显的加速效果，但不管是2线程还是4线程其加速比都达不到理想的2或者是4，这是因为在OpenMP中线程的开启和关闭会带来一定的时间开销，又因为4线程中的线程开销比2线程的更大，所以在上表中4线程的加速比没有2线程的加速比理想.同时，随着问题规模的增大，4线的加速比又逐渐变好，这是因为线程的开销所占用的时间比例会随着问题规模的增大而逐渐减小，从而在较大规模的问题上会有比较好的加速比.

表7 并行优化运行时间统计表

3.3 访存优化运行时间对比与分析

在并行优化的基础上，利用如图4的优化框架对遗传算法进行二次优化.经多次实验得出，在本实验中K值大约为12000的时候，效率能达到最好.

表8为最终的经过两次优化时间对比，在并行优化的基础上的访存优化后时间最多可以提高25.7%.而与最原始的串行时间对比，时间有了大幅的提高，例如在pr1002这个数据集上最终优化后的时间甚至能达到原始串行的1/5.

表8 二次优化时间对比

3.4 二次优化最优值对比与分析

为了达到对比效果，实验参数的设置同样为表6所示，同时依然也是每隔200代记录了一次当前中最优序列的路径长度并分别画出了其变化曲线，如图8、图9、图10所示，其数据为测试20次的平均值.

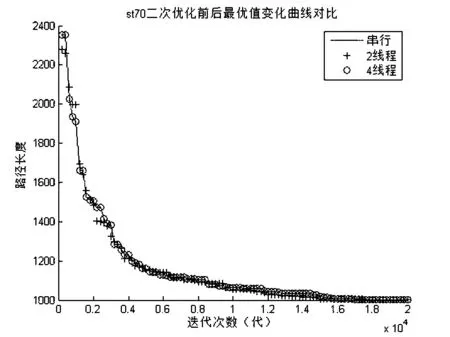
图8 st70二次优化前后最优值变化曲线对比

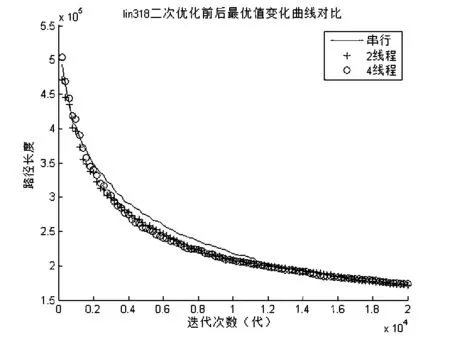
图9 lin318 二次优化前后最优值变化曲线对比

从图8、图9、图10可以看到，每种问题的三条曲线都是几乎重叠，说明本文的优化加速方法后并不影响其精度.同时，随着问题规模的增大，曲线的下降幅度也逐渐减少，说明对于标准遗传算法本身找到最优值的难度也越来越大，表9为其具体的数据统计.

图10 pr1002二次优化前后最优值变化曲线对比

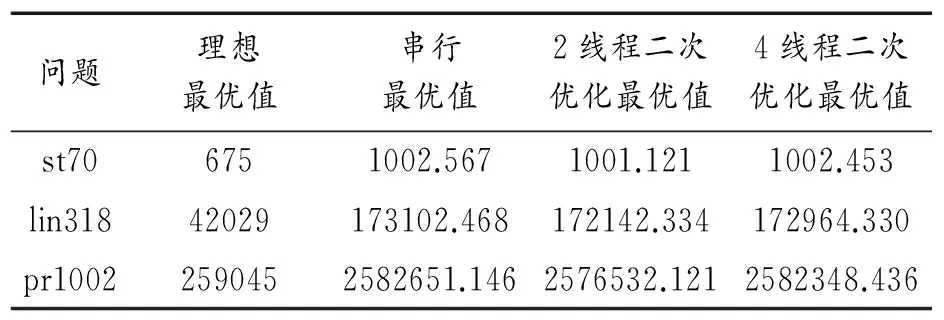
问题理想最优值串行最优值2线程二次优化最优值4线程二次优化最优值st706751002.5671001.1211002.453lin31842029173102.468172142.334172964.330pr10022590452582651.1462576532.1212582348.436

从表9可以看到，由于采用的标准遗传算法固有的缺点，实际得出来的结果与理想值有一定差距，特别是在318个城市和1002个城市即TSP问题规模较大时，差距尤为明显.

4 结束语

通过标准遗传算法的加速优化框架来解决TSP问题，最后通过实验证明该方法使得程序运行时间得到了大大减少，并且在优化前后，其得到的解都与原始串程序行相差无几，说明本文的优化方法是有效的.但由于标准遗传算法固有的一些缺陷，虽然时间上得到了很大程度的减少，但在得到的最优值上与理想值差距较大，但本文的框架适合应用于任何基于种群的优化算法.因此以后的研究方向将会是在算法层面上的改进或者选用更加理想的算法(比如蚁群算法)，再加上本文加速优化的方法使程序在时间上和最优值上都能达到更好的效果.

[1] 马永杰,云文霞.遗传算法研究进展[J].计算机应用研究,2012(4):11-15.

[2] HOLLAND JH.Adaptationinnaturalandartificialsystems:anintroductoryanalysiswithapplicationstobiology,control,andartificialintelligence[M] ．Cambridge: MIT Press,1992：23-25．

[3] 龚向坚,皱腊梅,胡义香.基于OpenMP的多核系统并行程序设计方法研究[J].南华大学学报:自然科学版,2013(1):64-69.

[4] J.Hennessy,D.Patterson.ComputerArchitecture:AQuantitativeApproach,2ndEdition[M].San Mateo,Calif:Morgan Kaufmann,1995:11-13.

[5]王 娜.求解TSP的改进遗传算法[D].西安:西安电子科技大学,2010:2-4.

[6] J.Grefenstete,et al.GeneticAlgorithmsfortheTravelingSalesmanProblem[C]//Int.Conf. On Genetic Algorithms and Applicantions,1985：154-168.

[7] Simianx M, Pataki L M.GeneticAlgorithms：ASurvey[J].Computer,1994：27.

[8] L . Davis.ApplyingAdaptiveAlgorithmstoEpistaticDomains[C]//Int. Joint Conf. on Artificial Intelligence.1985:162-164.

[9] Homaifar,S.Guan, and G.Liepins.ANewApproachontheTravelingSalesmanProblembyGeneticAlgorithms[C]//Int. Conf.On Gentic Algorithms,1993:460-466.

[10]Oliver L M,smith D J,Holland J R C.AstudyofPermutationCrossoverOperatorsontheTravelingSalsmanProblem[C]//In:Proceedings of the Second International Conference on Genetic Algorithms,1987:224-230.

[责任编辑 范 藻]

TSP Problems Solving Based on the Optimization and Memory Access Optimization Genetic Algorithm

LU You, HE Jia

(Chengdu University of Information Technology, Chengdu Sichuan 610025, China)

TSP (Traveling Salesman Problem) is one of several well-known problems in the field of graph theory, we solve this problem by using the standard genetic algorithm. However, due to the TSP problem solving using genetic algorithms is often more time-consuming, and with the increasing size of the TSP, time consumption also increased significantly. Therefore, this article uses the parallel optimization and optimization fetch two acceleration methods for genetic algorithm optimization from the code level to achieve the purpose of reducing the running time of the program, thereby increasing the efficiency of solving the TSP problem.Finally, the experimental method to verify the feasibility of accelerating from curves and tables herein terms of time.

Genetic Algorithm; TSP; parallel

2016-12-25

陆 游(1992—)，男，重庆梁平人.硕士研究生，主要从事计算机智能研究.

TP18

A

1674-5248(2017)02-0011-07