以生为本，奥妙无穷——谈六年级数学 “感悟”教学

文/佛山市南海区狮山镇颜峰小学 麦国新

为了贴近学生，我运用数形结合的思想，以引导学生画图分析的方法重新设计了这道题目的探究过程。 （如下图）

（1）在下列正方形中依次用阴影表示数列中的分数。

以生为本，奥妙无穷
——谈六年级数学 “感悟”教学

文/佛山市南海区狮山镇颜峰小学 麦国新

学习过程中的发现、感悟、体验与学习过程之后结出的 “果”同样重要。学生在获得对数学理解的同时，更要在认知、情感、能力等多方面得到发展。每个学生都是人格独立、个性丰富、思维活跃的个体，灌输型的教学很难适应 “以学生的发展为本”的新型课堂，新时期教育改革的浪潮呼唤 “感悟”型的教学。

一、问题导学，在挑战中感悟

学生没有迸发出思维火花的数学课不是一节好课，因此教师必须以问题为引领，在知识的探究过程中不断带给学生新颖有趣的挑战，激发他们产生尝试、操作、探究的冲动，使数学学习真正成为学生强烈的内在需求，进而调动他们全面参与问题的发现、提出、分析、解决的过程，从中感悟数学知识的生成和本质。

例如∶教学圆锥体积的时候，需要强化圆锥体积与圆柱体积之间的联系。教材要进行实验操作，从等底等高的圆锥里向圆柱里面倒水，倒3次刚好倒满，感悟圆锥的体积是圆柱的三分之一。

做完实验一后，我抓住时机，马上把问题 “升级”，进行精彩的变式练习： “这个问题大家学完了，老师来给你们新的挑战，你敢迎战吗？”。迅速激发了学生的好胜心和求知欲。进而提出下面的两个问题，引导学生自己进行试验探究。

实验二：反过来在圆柱装满水向圆锥倒水，可以倒满几个这样的圆锥？ （如下图）

实验三：如果把圆柱的高改为圆锥的2倍，底面积相同，可以倒满几个这样的圆锥？ （如下图）

通过这两个问题的深化，以实验操作突破难点，形象直观地理解和记忆知识。学生对 “等底等高的圆锥体积是圆柱的三分之一”这个难点的感悟不断突破，不断深化。理解到这个命题反过来表述就是“等底等高的圆柱体积是圆锥的3倍”。在不知不觉中就从正反两面理解了教学难点，同时还享受到探索活动的乐趣，感受到原来枯燥无味的数学也可以学的这么有趣。

二、操作探究，在情景中感悟

数学学习只有做到放手让学生探索、发现，并在探究过程中体验认知、情感、技能、态度的协同发展，才是真正有意义的数学学习。教师的教学要从 “以题为本”向“以生为本”转变。让学生自己主动参与学习活动，在动态的过程中感悟数学知识的生成，同时获得良好的数学学习体验。

这道题需要渗透无限逼近0的极限思想。这对于小学生来说非常抽象，感到不可理解。它的数学模型是，用小学生的知识水平理解就是，

为了贴近学生，我运用数形结合的思想，以引导学生画图分析的方法重新设计了这道题目的探究过程。 （如下图）

（1）在下列正方形中依次用阴影表示数列中的分数。

（2）这列数的每一项越来越大还是越来越小?能写得完吗？

（3）依次观察各数对应的正方形中的阴影，你发现了什么规律？

通过自主画图分析，操作感悟。学生很容易就直观地理解了“这列数越来越小，无限接近0，但永远没有尽头”这一难点。本来遥不可及的抽象数学难题也就迎刃而解了。学生不但找到了规律，更可贵的是学到了数形结合、画图分析的数学方法，积累了数学研究经验，同时还发展了学生的模型思想，很好地体现并落实了新课标对“四基”的要求。

三、联系沟通，在迁移同化中感悟

学习的本质就是不断用旧有的知识经验来解释和同化新知识的过程。学习成功的关键是在未知知识和已有的经验之间架起桥梁，找到并建立它们之间的实质联系，让学生站在原来的起点“跳一跳就摘到桃子”。

六年级新教材强化了分数和小数的乘法约分训练。例如：直接写出得数。

一些学生对于分数乘小数的约分方法不熟悉，计算能力灵活性差，有的甚至把1.2化成分数来计算，十分繁琐。

我在教学中设计了这样的导学提纲，让学生小组讨论。

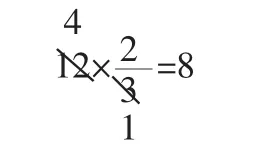
3.你认为整数中的约分方法在分数和小数相乘时可以使用吗？有什么前提条件？

这样的教学善于把握学生学习的切入点，成功架设新旧知识之间的桥梁；引导学生联系沟通新旧知识，发现窍门并生成 “顿悟”。学生在不知不觉中经历着知识经验的迁移、同化，知识结构得以拓展、整合；在解决问题的过程中既获得了知识，又发展了类比思维，充分体验到了自主探究、收获成果的快乐。

四、提炼积累，在回顾与反思中感悟

新课程标准把数学课堂中的回顾反思放在重要的位置。新教材专门设计了回顾反思的教学环节，教师每节课要留一定的时间给学生，让他们经历回顾总结、反思、辩论的过程，最后要以数学经验、思想方法的积累结束。长期坚持下来，对促进学生数学思维发展和解决问题能力的提升大有帮助。因此教师要每节课利用这一环节总结积累数学方法和经验，提炼数学思想。

例如：从六年级解方程的教学来看，教材是运用等式的性质解方程 （如例1）。但还有相当部分的学生用四则运算各部分间关系去解题，这也反映了一些教师的教学取向。问题是有的中下层次的学生用各部分间关系去解方程，却记错各部分数量间的关系造成错误 （如例2）。

因此我在教完运用等式的性质解方程后，补充介绍了运用四则运算各部分间的六种关系解方程。着重引导学生对比和反思两个问题，引起学生更深层次的思考和辩论：

（1）你更喜欢哪一种方法？优点是什么？缺点呢？

（2）教材为什么不用后者而要用前者解方程？

第一个问题尊重学生的认知主体地位，对比代数方法和用数量关系解法的异同，引导他们说出喜欢的原因再分析其缺点。通过反思、讨论。大家的共识是：喜欢用四则运算各部分间关系的学生很明显就是因为喜欢它写的少。但它的缺点是要记忆六个关系式，很容易记错。喜欢用等式的性质去解的学生是因为方法简单，不用死记，但它的缺点是写得比较长。

第二个问题引起学生激烈的争论。通过大量的错题例子 （如前），学生明白到运用四则运算各部分间的六种关系解方程，可能会因为记忆数量关系不准确造成的错误。但是用等式的性质去解方程，它的知识价值主要还是降低难度，抵消掉方程中含有未知数一边中的数就可以了，加了什么就减去什么，乘了什么就除以什么，非常容易记忆。所以教材选择了运用等式的性质解方程。

“道理越辩越明白”，学生通过争论深刻感悟到代数方法的优越性，明白了编者的意图。结论是用四则运算各部分间关系的解法了解一下无妨，但最好还是用等式性质的解法，因为它好用易记。

五、体验错误，在失败中感悟

俗话说得好：失败是成功之母。许多重大的科学发现都是经历了无数挫折、苦苦求索后才得出的。爱迪生为了发明电灯，做了一千五百多次实验都没有找到适合的灯丝，嘲笑他的人说： “爱迪生先生，你已经失败了一千五百多次了。”爱迪生回答： “不，我没有失败，我的成就是发现了一千五百多种材料不适合做电灯灯丝。”在试用了6000多种纤维材料，经历无数次失败后他终于用日本竹丝点燃了第一盏有广泛实用价值的电灯。

这个故事告诉我们不怕挫折，善于从失败中总结经验的人才能取得成功；而失败的经验也是一笔宝贵的财富。真正的科学研究往往不会一帆风顺，最需要的正是百“错”不挠、上下求索的精神和思维品质，数学的探究也不例外。反思我们的数学课堂教学，有的教师怕学生出错，也怕影响了教学进度，所以步步扶持，按部就班，学生犯错的机会很少。结果正面灌输的味道就太浓，贴近真实数学研究的味道就太淡。新课标“四基”中的一条就是 “获得基本的数学活动经验”，经验从何而来？体验错误就是一个重要的途径。因此我在教学中努力实践两个原则：放手让学生尝试，给他们 “犯错”的机会；对待错误，要鼓励学生从中找到有价值的东西。

责任编辑 罗 峰