微分法求切线方程在高等数学中的应用

郝连军

辽宁石化职业技术学院

微分法求切线方程在高等数学中的应用

郝连军

辽宁石化职业技术学院

高等数学中求曲线（或曲面）的切线（或切面）方程是学生必须掌握的知识，但是对于初学者掌握起来有一定难度，随着学习的深入我们可以利用更简洁的方法来解决这一方面的问题。根据导数的几何意义，在很小的范围内，可以利用切线代替小曲线，也就是以直带曲。这样可以利用微分学的知识化微分为增量（差分）的方法，求曲线（或曲面）的切线（或切面）方程。本文向大家介绍一种简便方法——改微分求切法线（或切面）法．这个方法简便易行，是以直代曲的一个典型方法．我们从四个方面举例说明．

微分；切线；法线；微分求切线；高等数学

1、改微分求切法线（或切面）的原理和步骤

定理：光滑曲线y=f(x)在x0点与其切线有相同的微分，且这个微分就是对应切线的增量。

证明：曲线y=f(x)在(x0,y0)点切线的斜率k=f′(x0)；

曲线y=f(x)过点(x0,y0)的切线方程是Y=y0+f′(x0)(x-x0)；

该切线方程在点(x0,y0)处的微分为dY=f′(x0)dx与曲线y=f(x)在点(x0,y0)处的微分是dy=f′(x0)dx相等。

再有Y=y0+f′(x0)(x-x0)是关于x的线性函数，且dx=△x，故△y=dy，所以△y=dy=dY=△Y。

这其实就是微分的几何解释，不过现在我们是换了一个角度来看这个事实，从而为求切线铺平了道路，根据这个定理，曲线y=f(x)在点x0的微分可以看作其切线在该点的微分，进而可看成切线在x0点对应于dx=△x的增量，然后把增量改成对应的差的形式，就得到曲线过(x0,y0)点的切线的方程。

由此可给求出曲线切线及曲面切平面的一个简单方法——改微分求切法线（或切面）法，这个方法不论是对曲线或曲面，也不论其形式是方程或方程组，都照样适用。

改微分求切法线（或切面）的步骤如下：

(1)先求曲线(或曲面)方程在给定点微分；

(2)再将微分改为增量，进而改为相应的差式便得到切线(或切平面)方程；

(3)借助解析几何知识，进而得到与其相关的法平面(或法线)的方程。

2、改微分求切法线（或切面）法的应用

（一）求显函数曲线y=f(x)过点p0(x0,y0)的切线方程和法线方程。

（1）对曲线方程y=f(x)在点p0(x0,y0)处微分得dy=f′(x0)dx

式子（1）就是所求的切线方程。

因为过p0(x0,y0)点的法线斜率于此切线斜率互为负倒数，故所求法线方程为：

当f′(x0)=0时，法线方程为x=x0。

例1、求曲线y=x3+3x-8在x=2处的切线的方程和法线方程。

解：改微分求切法线法。

对曲线y=x3+3x-8在x=2处求微分得：

dy=3×4dx+3dx即15dx-dy=0。

改微分为增量得15(x-2)-(y-6)=0即15x-y-24=0这就是所求的切线方程。

（二）求隐函数曲线F(x,y)=0过点p0(x0,y0)的切线方程和法线方程。

（1）对曲线方程F(x,y)=0在点p0(x0,y0)处求微分得：

F′x(x0,y0)dx+F′y(x0,y0)dy=0

（2）改微分为增量得：

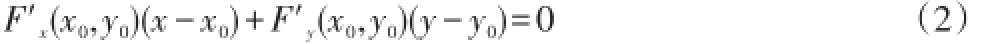
式子（2）就是所求的切线方程。

由此可得所求法线的法向量为：

化简得：5x+2y-7=0

（三）求显函数曲面z=f(x,y)过点p0(x0,y0,z0)的切平面和法线方程。

（1）若方程z=f(x,y)在点p0(x0,y0,z0)存在偏导数，对方程z=f(x,y)在p0(x0,y0,z0)点微分得:

dz=f′x(x0,y0)dx+f′y(x0,y0)dy

（2）改微分为增量得

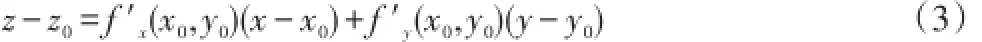
式子（3）就是所求的切平面方程。

例2求曲线y3+y2=2x在（1，1）点处的切线和法线方程。

解：改微分求切法线。

对曲线y3+y2=2x在（1，1）点处求微分得：

3dy+2dy=2dx

即：

2dx-5dy=0

改微分为增量得：

2(x-1)-5(y-1)=0

即：

2x-5y+3=0

这就是所求的切线方程。

法线方程为因为平面法向量为：