2016年中考“事件的概率”专题解题评析

王华

（浙江省台州市黄岩澄江中学）

2016年中考“事件的概率”专题解题评析

王华

（浙江省台州市黄岩澄江中学）

通过对2016年各地中考试卷的分析，对呈现的亮点进行点评，梳理出解题的方法和策略，提炼出命题的规律和方向，为高效复习提供参考和建议.

中考试题；事件概率；解题评析；教学建议

《义务教育数学课程标准（2011年版）》中关于事件的概率提到两点：（1）能通过列表、画树状图等方法列出简单随机事件所有可能的结果，以及指定事件发生的所有可能结果，了解事件的概率.（2）知道通过大量的重复试验，可以用频率来估计概率.各地对“事件的概率”的考查基本上围绕着这两点展开，不但注重对概率基础知识和基本技能的考查，也注重概率思想和基本活动经验的考查.

一、典例分析

2016年各地的中考试卷，关于“事件的概率”的考查整体稳定，重点强调在丰富的情境中提炼出数学模型，利用概率的核心知识解决问题，这一趋势将继续延续下去.

1.关注随机事件，理解概率意义

例1（辽宁·沈阳卷）“射击运动员射击一次，命中靶心”这个事件是（ ）.

（A）确定事件 （B）必然事件

（C）不可能事件 （D）不确定事件

解：“射击运动员射击一次，命中靶心”这个事件是随机事件，属于不确定事件.

故选D.

例2（湖北·武汉卷）不透明的袋子中装有形状、大小、质地完全相同的6个球，其中4个黑球、2个白球，从袋子中一次摸出3个球，下列事件是不可能事件的是（ ）.

（A）摸出的是3个白球

（B）摸出的是3个黑球

（C）摸出的是2个白球、1个黑球

（D）摸出的是2个黑球、1个白球

解：因为袋子中有4个黑球，2个白球，所以摸出的黑球个数不能超过4个，摸出白球的个数不能超过2个.选项A摸出的白球个数是3个，超过2个，是不可能事件.

故选A.

【评析】这两道例题考查的是必然事件、不可能事件、随机事件的概念.必然事件是指在一定条件下，一定发生的事件.不可能事件是指在一定条件下，一定不发生的事件.不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件.这两道例题的亮点在于让学生先想象结果的可能性，然后结合事件的概念进行解答.

例3（湖北·宜昌卷）在课外实践活动中，甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率，其实验次数分别为10次、50次、100次、200次，其中实验相对科学的是（ ）.

（A）甲组 （B）乙组

（C）丙组 （D）丁组

解：选D.

例4（福建·福州卷）下列说法中，正确的是（ ）.

（A）不可能事件发生的概率为0

（C）概率很小的事件不可能发生

（D）投掷一枚质地均匀的硬币100次，正面朝上的次数一定为50次

解：选项A不可能事件发生的概率为0，所以选项A正确；选项B随机事件发生的概率在0与1之间，所以选项B错误；选项C概率很小的事件不是不可能发生，而是发生的可能性比较小，所以选项C错误；选项D投掷一枚质地均匀的硬币100次，正面朝上的次数可能为50次，所以选项D错误.

故选A.

【评析】这两道例题考查概率的意义：一般地，在大量独立重复实验中，如果事件A发生的频率稳定在某个常数p附近，那么这个常数p就叫做事件A的概率，记为P（A）=p.必然发生的事件的概率P（A）=1；不可能发生事件的概率P（A）=0.频率和概率是两个不同的概念，但是却有必然的联系.这两道例题的亮点在于考查概率的意义，概率与频率的关系.

2.注重基础，用列举法求概率

（1）用直接枚举的方法求简单随机事件的概率.

例5（江苏·南京卷）某景区7月1日—7月7日一周天气预报如图1所示，小丽打算选择这期间的一天或两天去该景区旅游，求下列事件的概率.

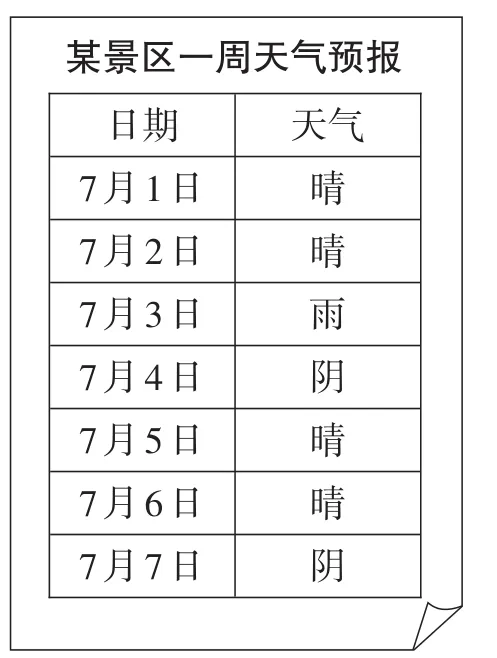
图1

（1）随机选择一天，恰好天气预报是晴；

（2）随机选择连续的两天，恰好天气预报都是晴.

解：（1）随机选择一天，天气预报可能出现的结果有7种，即7月1日晴、7月2日晴、7月3日雨、7月4日阴、7月5日晴、7月6日晴、7月7日阴，并且它们出现的可能性相等.恰好天气预报是晴（记为事件A）的结果有4种，即7月1日晴、7月2日晴、7月5日晴、7月6日晴，所以P（A）＝.

（2）随机选择连续的两天，天气预报可能出现的结果有6种，即（7月1日晴，7月2日晴），（7月2日晴，7月3日雨），（7月3日雨，7月4日阴），（7月4日阴，7月5日晴），（7月5日晴，7月6日晴），（7月6日晴，7月7日阴），并且它们出现的可能性相等.恰好天气预报都是晴（记为事件B）的结果有2种，即（7月1日晴，7月2日晴），（7月5日晴，7月6日晴），所以P（B）=.

例6（山东·济宁卷）如图2，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任意选取一个白色的小正方形并涂黑，使黑色部分的图形仍然构成一个轴对称图形的概率是（ ）.

图2

解：在4×4的正方形网格中，任选取一个白色的小正方形并涂黑，共有13种等可能的结果，使图中黑色部分的图形构成一个轴对称图形的有5种（如图3）.

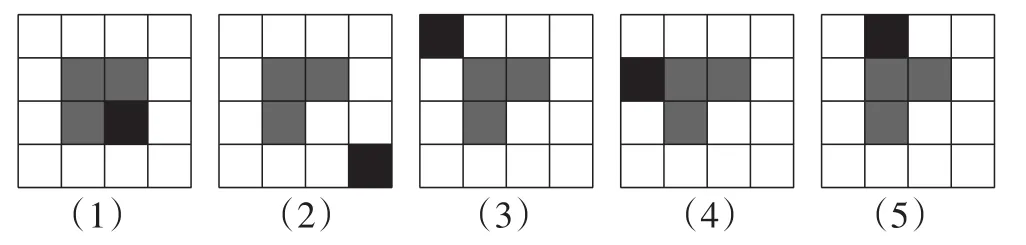
图3

所以使图中黑色部分的图形仍然构成一个轴对称图形的概率P=.

故选B.

【评析】这两道例题都是先明确简单随机事件的所有可能结果，找出当前事件的所有可能结果，从而求出概率，难度不大，关键是学生需要明确所有可能出现的结果数，以及当前事件出现的结果数，利用概率的概念解答.

（2）用列表法或画树状图法求概率.

例7（山东·威海卷）一个盒子里有标号分别为1，2，3，4，5，6的六个小球，这些小球除标号数字外都相同.

（1）从盒中随机摸出一个小球，求摸到标号数字为奇数的小球的概率；

（2）甲、乙两人用这六个小球玩摸球游戏，规则是：甲从盒中随机摸出一个小球，记下标号数字后放回盒里，充分摇匀后，乙再从盒中随机摸出一个小球，并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数，则判甲赢；若两次摸到小球的标号数字为一奇一偶，则判乙赢.试用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.

解：（1）因为有6个小球，所以摸到标号数字为奇数的小球的概率；

（2）先列表（如表1）.

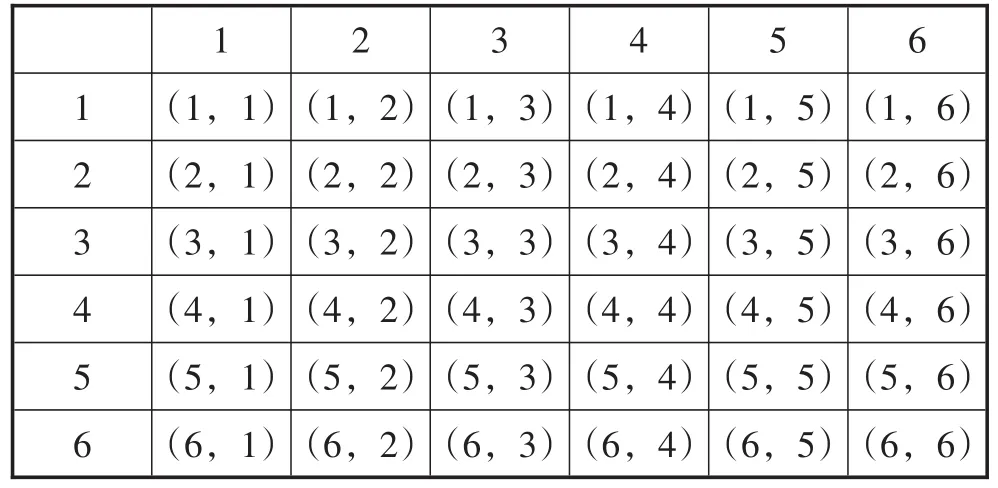
表1

共有36种等可能的情况，两次摸到小球的标号数字同为奇数或同为偶数的有18种，摸到小球的标号数字为一奇一偶的结果有18种，

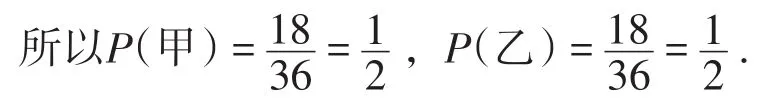
这个游戏对甲、乙两人是公平的.

例8（云南卷）某超市为庆祝开业举办大酬宾抽奖活动，凡在开业当天进店购物的顾客，都能获得一次抽奖的机会，抽奖规则如下：在一个不透明的盒子里装有分别标有数字1，2，3，4的四个小球，它们的形状、大小、质地完全相同，顾客先从盒子里随机取出一个小球，记下小球上标有的数字，然后把小球放回盒子并搅拌均匀，再从盒子中随机取出一个小球，记下小球上标有的数字，并计算两次记下的数字之和，若两次所得的数字之和为8，则可获得50元代金券一张；若所得的数字之和为6，则可获得30元代金券一张；若所得的数字之和为5，则可获得15元代金券一张；其他情况都不中奖.

（1）试用列表或画树状图（树状图也称树形图）的方法（选其中一种即可），把抽奖一次可能出现的结果表示出来；

（2）假如你参加了该超市开业当天的一次抽奖活动，求能中奖的概率P.

解：（1）列表如表2所示.

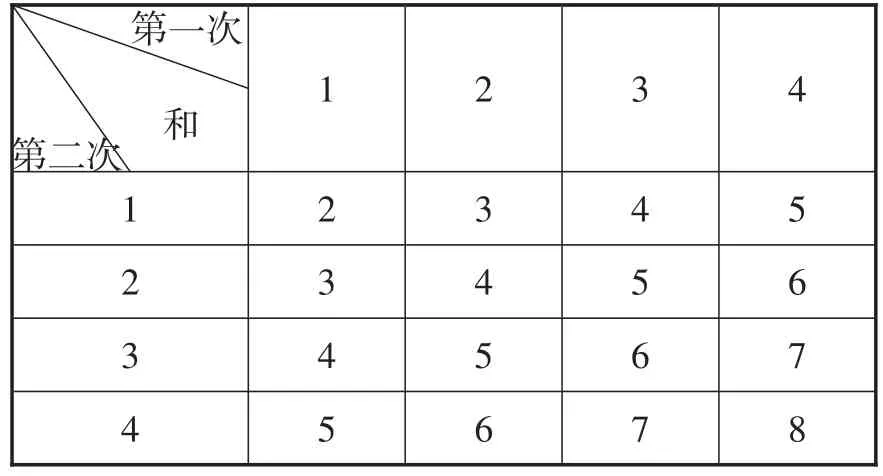
表2

（2）由列表可知，一共有16种等可能的结果，其中两次所得数字之和为8，6，5的结果有8种，所以抽奖一次中奖的概率

抽奖一次能中奖的概率P=.

【评析】这两道例题都可以用列表法或者画树状图法来解决问题，例7有6个小球，且分2次摸，故用画树状图法就显得比较“拥挤”，用列表法比较清晰；例8用列表法可以直接计算结果.一般情况下对于2步抽取问题，优先采用列表法.首先根据题意画出表格，列出所有可能的结果数n，再从中选出符合事件结果数m，求出概率.

例9（湖北·黄石卷）如图4，一只蚂蚁从点A出发到点D，E，F处寻觅食物.假定蚂蚁在每个岔路口都会随机地选择一条向左下或右下的路径（如A岔路口可以向左下到达B处，也可以向右下到达C处，其中A，B，C都是岔路口）.那么，蚂蚁从点A出发到达点E处的概率是_______.

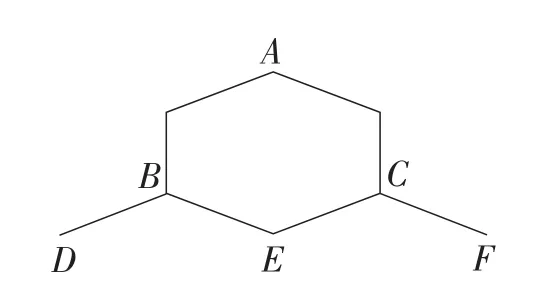
图4

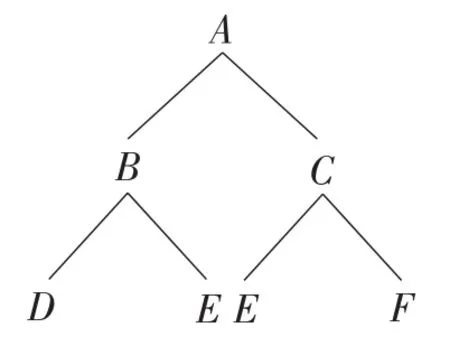
图5

解：画树状图如图5所示.

一共有4种等可能的结果，蚂蚁从点A出发到达点E处的情况有2种，所以蚂蚁从点A出发到达点E处的概率P=.

例10（浙江·金华卷）小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为（ ）.

解：记“打扫社区卫生”为A，“参加社会调查”为B，画树状图如图6所示.

由树状图可知，共有4种等可能的结果，两人同时选择“参加社会调查”（即BB）的结果有1种.所以两人同时选择“参加社会调查”的概率P=.

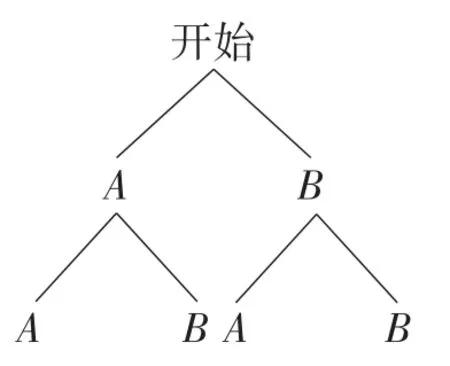
图6

故选A.

【评析】这两道例题的亮点在于，不管是小蚂蚁觅食的问题，还是两人同时选择“参加社会调查”的问题，本质上与“抛两次硬币，求两次正面朝上的概率”相同，用画树状图法可以比较方便地解决问题.

例11（内蒙古·包头卷）同时抛掷三枚质地均匀的硬币，至少有两枚硬币正面向上的概率是（ ）.

解：硬币正面朝上记为“正”，正面朝下记为“反”，画出树状图如图7所示.

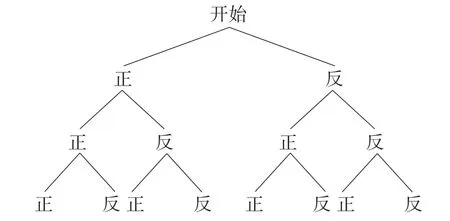
图7

由树状图可知，同时抛掷三枚质地均匀的硬币共有8种等可能的结果，至少有两枚硬币正面向上的结果有4种.

故选D.

例12（江苏·扬州卷）小明、小刚和小红打算各自随机选择本周日的上午或下午去扬州马可波罗花世界游玩.

（1）小明和小刚都在本周日上午去游玩的概率为________；

（2）求他们三人在同一个半天去游玩的概率.

解：（1）上午记为“上”，下午记为“下”，画出树状图如图8所示.

图8

由树状图可知，三人随机选择本周日的上午或下午去游玩共有8种等可能结果，其中小明和小刚都在本周日上午去游玩的结果有（上，上，上）（上，上，下）2种.所以小明和小刚都在本周日上午去游玩的概率

（2）他们三人在同一个半天去游玩的结果有（上，上，上）（下，下，下）这2种，所以他们三人在同一个半天去游玩的概率

【评析】这两道例题一次试验涉及3步，此时列表法就不方便了，为不重不漏地列出所有可能的结果，通常采用画树状图法.所以在一次试验涉及3步或更多步时，我们一般是先根据题意画出树状图，然后根据概率的概念进行解答.

例13（安徽卷）一袋中装有形状大小都相同的四个小球，每个小球上各标有一个数字，分别是1，4，7，8.现规定从袋中任取一个小球，对应的数字作为一个两位数的个位数；然后将小球放回袋中并搅拌均匀，再任取一个小球，对应的数字作为这个两位数的十位数.

（1）写出按上述规定得到所有可能的两位数；

（2）从这些两位数中任取一个，求其算术平方根大于4且小于7的概率.

解：（1）（方法1：列表法）如表3所示.

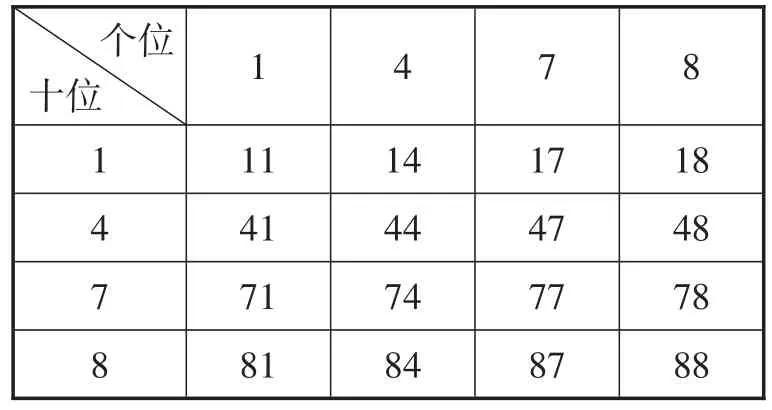
表3

（方法2：画树状图法）如图9所示.

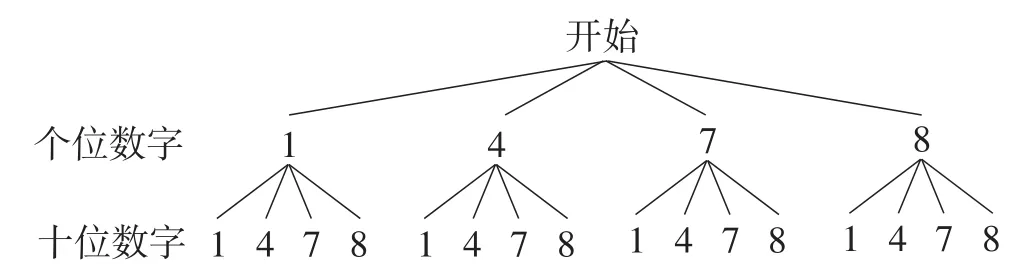
图9

共有16种等可能的结果数，它们是11，41，71，81，14，44，74，84，17，47，77，87，18，48，78，88.

（2）算术平方根大于4，且小于7的结果有6种，所以算术平方根大于4且小于7的概率是

例14（甘肃·兰州卷）小明和小军两人一起做游戏，游戏规则如下：每人从1，2，…，8中任意选择一个数字，然后两人各转动一次如图10所示的转盘（转盘被分为面积相等的四个扇形），两人转出的数字之和等于谁事先选择的数，谁就获胜；若两人转出的数字之和不等于他们各自选择的数，就再做一次上述游戏，直至决出胜负.若小军事先选择的数是5，用列表法或画树状图的方法求他获胜的概率.

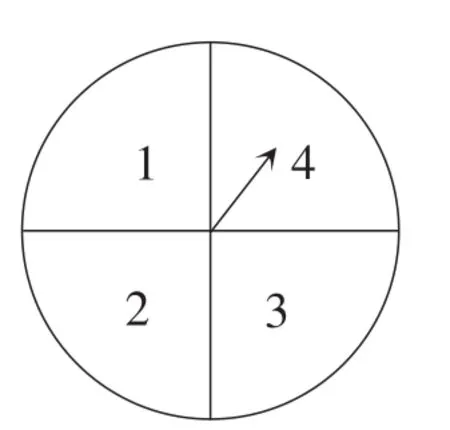
图10

解：（1）（方法1：列表法）如表4所示.

表4

（方法2：画树状图法）如图11所示.

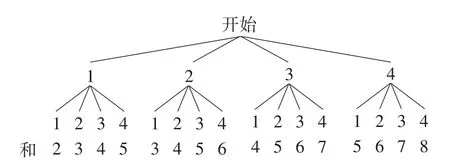
图11

共有16种等可能的结果，选择的数是5的有4种，

【评析】这两道例题都是放回抽样的模型，都可以用列表法、画树状图法来解题，放回抽样体现的特点是，列表法的表格中“对角线”是有内容的，画树状图时每一次分支数是相同的，抓住这一点，能够提高解题的准确率.

例15（海南卷）三张外观相同的卡片分别标有数字1，2，3，从中随机一次抽出两张，这两张卡片上的数字恰好都小于3的概率是（ ）.

解：（方法1：列表法）如表5所示.

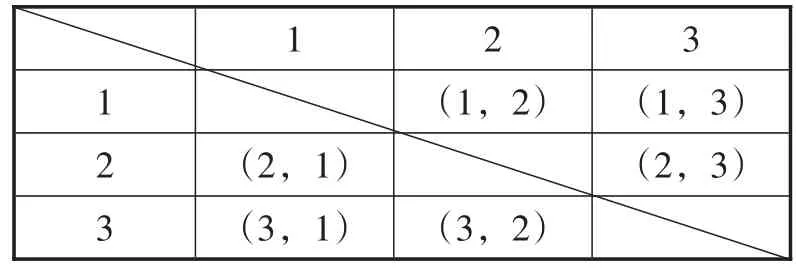
表5

（方法2：画树状图法）如图12所示.

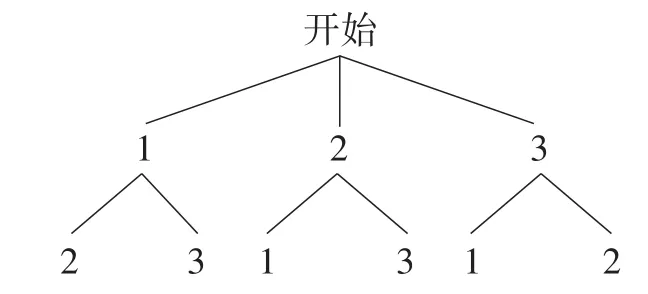
图12

共有6种等可能的结果，两张卡片上的数字恰好都小于3的结果有2种，所以两张卡片上的数字恰好都小于3的概率.

例16（江苏·宿迁卷）在一只不透明的袋子中装有2个白球和2个黑球，这些球除颜色外都相同.

（1）若先从袋子中拿走m个白球，这时从袋子中随机摸出一个球是黑球的事件为“必然事件”，则m的值为_______；

（2）若将袋子中的球搅匀后随机摸出1个球（不放回），再从袋中余下的3个球中随机摸出1个球，求两次摸到的球颜色相同的概率.

解：（1）因为在一只不透明的袋子中装有2个白球和2个黑球，这些球除颜色外都相同，从袋子中拿走m个白球，这时从袋子中随机摸出一个球是黑球的事件为“必然事件”，所以透明的袋子中装的都是黑球.所以m的值为2.

（2）设黑球分别为H1，H2，白球分别为B1，B2，

（方法1：列表法）如表6所示.

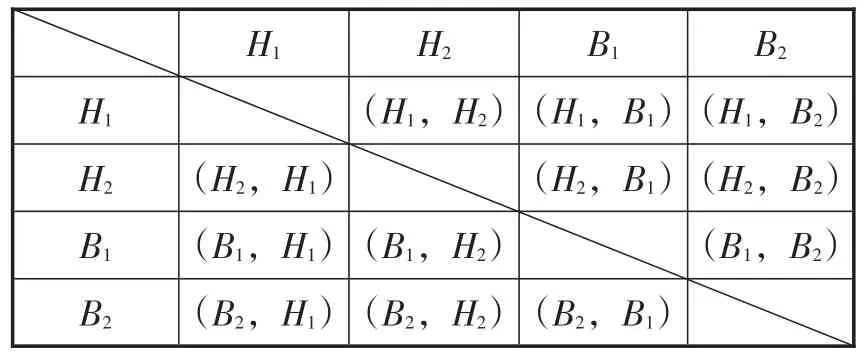
表6

（方法2：画树状图法）如图13所示.

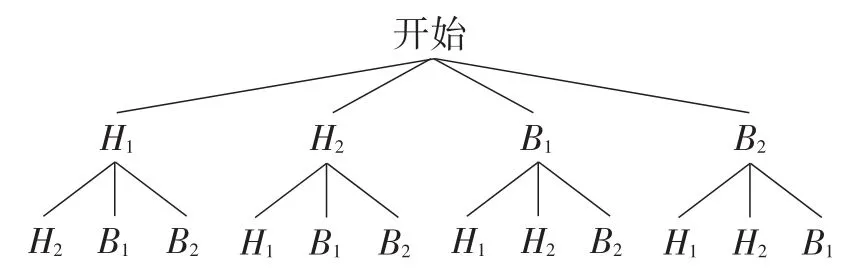
图13

共有12种等可能的结果，两次都摸到颜色相同的球的结果有4种，所以两次摸到的球颜色相同的概率是

【评析】这两道例题都是不放回抽样的类型，都可以用列表法、画树状图法来解题，不放回抽样体现的特点是，列表法的表格中“对角线”是没有内容的，画树状图时，分支会每次减少一支，解题时要注意是放回试验还是不放回试验.

3.基于统计思想，频率估计概率

例17（湖北·襄阳卷）一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球.每次摇匀后随机摸出1个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球的个数为_____.

解：因为频率稳定于概率，

所以可以估计摸到红球的概率是0.4，摸到黑球或白球的概率为1-0.4=0.6.

所以估计总的球数为（8+4）÷0.6=20.

所以估计红球的个数有20-（8+4）=8（个）.

例18（山西卷）每年5月的第二周为“职业教育活动周”，今年我省展开了以“弘扬工匠精神，打造技能强国”为主题的系列活动，活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动，相关职业技术人员进行了现场演示，活动后该校随机抽取了部分学生进行调查：你最感兴趣的一种职业技能是什么？并对此进行了统计，绘制了统计图（均不完整）如图14所示.

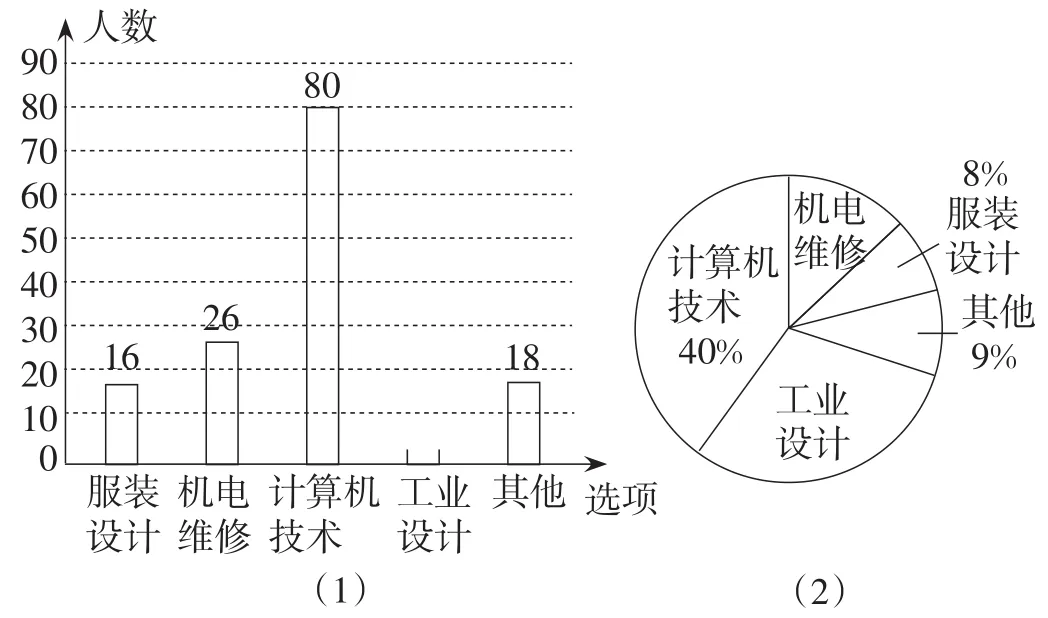
图14

（1）补全条形统计图和扇形统计图；

（2）若该校共有1800名学生，试估计该校对“工业设计”最感兴趣的学生有人数有多少？

（3）要从这些被调查的学生中随机抽取一人进行访谈，那么正好抽到对“机电维修”最感兴趣的学生的概率是_______.

解：（1）补全的扇形统计图和条形统计图如图15所示.

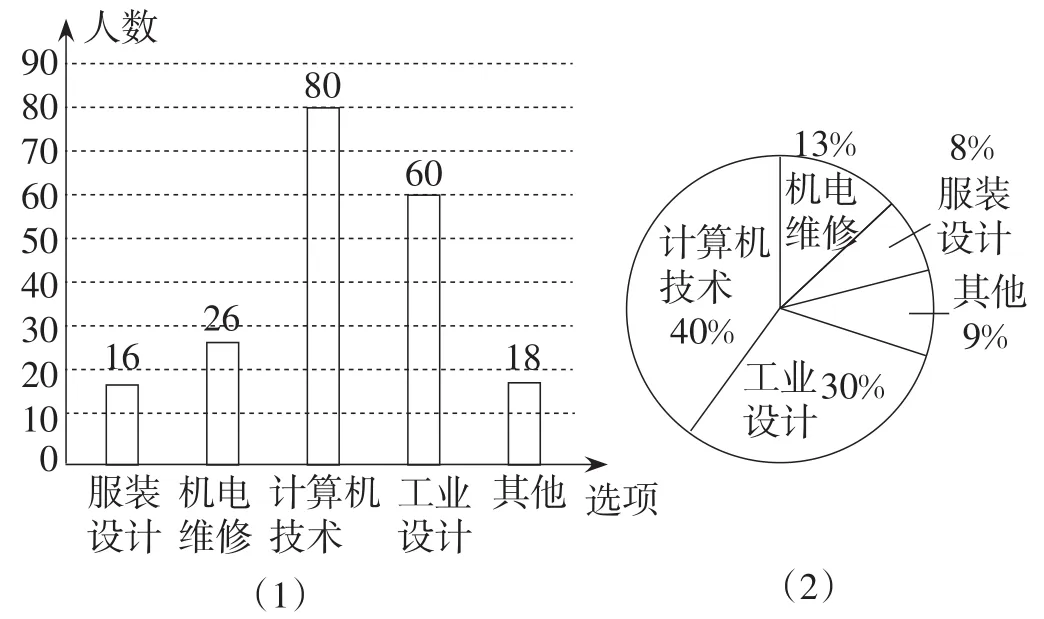
图15

（2）1800×30%=540（人）.

所以估计该校对“工业设计”最感兴趣的学生人数是540人.

（3）要从这些被调查的学生中随机抽取一人进行访谈，那么正好抽到对“机电维修”最感兴趣的学生的概率是0.13.

【评析】这两道例题考查样本估计总体，试题的背景贴近生活实际，注重概率知识在解决实际问题中的作用，需要学生深刻理解频率和概率之间的联系，频率稳定于概率，频率之和等于1，概率之和等于1.

例19（四川·达州卷）达州市图书馆今年4月23日开放以来，受到市民的广泛关注.5月底，八年级（1）班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计，并制成了如图16、表7所示的不完整的统计图表.

图16

表7：八年级（1）班学生去新图书馆的次数统计表

试根据统计图表中的信息，解答下列问题：

（1）填空：a=________，b=________；

（2）求扇形统计图中“0次”的扇形所占圆心角的度数；

（3）从全班去过该图书馆的同学中随机抽取1人，谈谈对新图书馆的印象和感受.求恰好抽中去过“4次及以上”的同学的概率.

解：（1）该班学生总数为12÷24%=50（人），

则a=50-8-12-10-4=16，

（3）从全班去过该图书馆的同学中随机抽取1人，有50-8=42种等可能结果，其中恰好抽中去过“4次及以上”的同学有4种结果，所以恰好抽中去过“4次及以上”的同学的概率

例20（山东·枣庄卷）小军同学在学校组织的社会实践活动中，负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了如表8所示的样本的频数分布表.

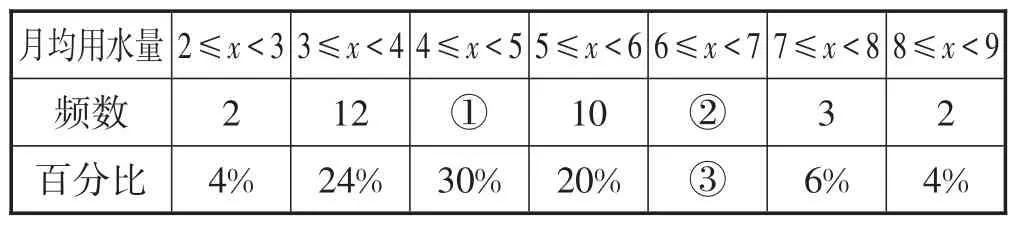
表8

（1）根据题中已有的信息补全频数分布表：

①________，②________，③________；

（2）如果家庭月均用水量大于或等于5 t，且小于8 t为“用水量中等”的家庭，通过样本估计总体，试问用水量中等的家庭的户数大约有多少？

（3）记月均用水量在2≤x＜3范围内的两户为a1，a2，在7≤x＜8范围内3户为b1，b2，b3，从这5户家庭中任意抽取2户，并求出抽取的2户家庭来自用水量在不同范围的概率.

解：（1）①50×30%=15；

②50-2-12-15-10-3-2=6；

③6÷50=0.12=12%.

（2）中等用水量家庭大约有450×（20%+12%+ 6%）=171（户）.

（3）列表如表9所示.

表9

由列表法可知，总共有20种等可能的结果，其中2户家庭来自不同范围的有12种.所以抽取的2户家庭来自不同范围的概率

【评析】这两道例题是统计与概率相结合的问题，考查学生从统计图表中获取信息的能力，必须认真观察、分析才能获取有用的信息，让学生经历了统计分析和概率计算活动，强化了综合运用统计与概率解决实际问题能力的考查.

4.把几何概率转化为古典概率求解

例21（新疆卷）小球在如图17所示的地板上自由滚动，并随机停留在某块正方形的地砖上，则它停在白色地砖上的概率是________.

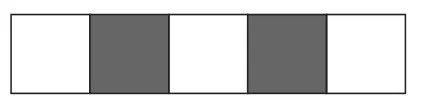
图17

解：由图可知，共有5块瓷砖，白色的有3块，所以它停在白色地砖上的概率P=.

例22（江苏·扬州卷）如图18所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成，一只小鸟在广场上随机停留，刚好落在黑色三角形区域的概率为________.

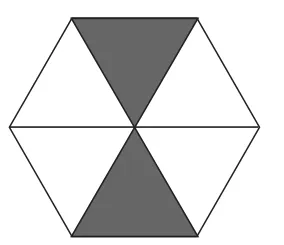
图18

解：落在黑色三角形上的概率就是黑色三角形面积与总面积的比值，因为黑色三角形的面积占总面积的，所以刚好落在黑色三角形区域的概率P=.

【评析】这两道例题的背景是几何概率的模型.通过观察出白（黑）色方砖在整个地板（广场）中所占的比值后直接得出结论，属简单题目.通过平面图形的均匀分割转化为古典概率的模型，体现了转化和化归的数学思想.

例23（山东·青岛卷）小明和小亮用如图19所示的两个可以自由转动的转盘做游戏，每个转盘被分成面积相等的几个扇形.转动两个转盘各一次，若两次数字之积大于2，则小明胜，否则小亮胜.这个游戏对双方公平吗？说明理由.

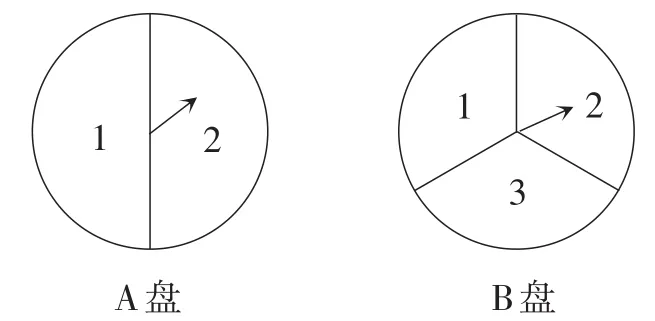
图19

解：先列表如表10所示.

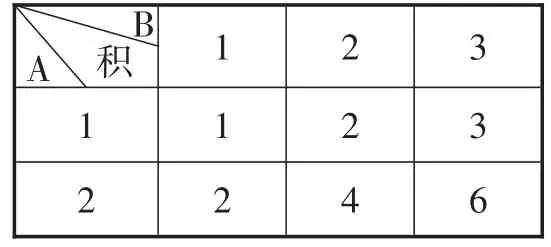
表10

由列表法可知，共有6种等可能的结果，积大于2的有3种，

所以这个游戏对双方是公平的.

例24（山西卷）如图20，是一个能自由转动的正六边形转盘，这个转盘被三条分割线分成形状相同、面积相等的三部分，且分别标有“1”“2”“3”三个数字，指针的位置固定不动.让转盘自动转动两次，当指针指向的数都是奇数的概率为________.

图20

解：列表如表11所示.

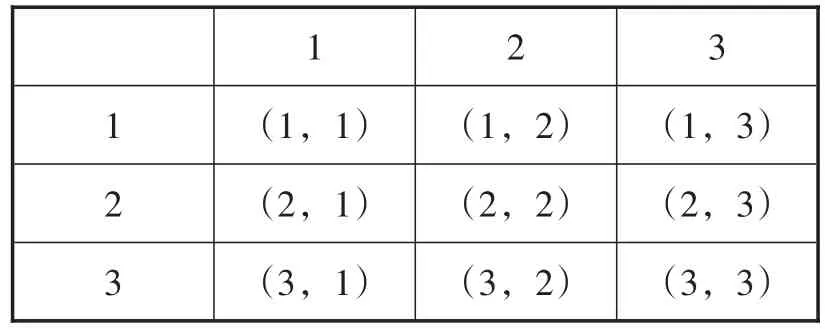
表11

共有9种等可能的结果，指针指向的数都是奇数有4种，所以指针指向的数都是奇数的概率

【评析】这两道例题的背景是转盘，转盘有关的概率问题在历年的试卷中大量出现，转盘可以看作是几何概率，但如果分析本质，无非还是通过平面图形的均匀分割转化为古典概率的模型，用列表法依然可以清晰的解决问题.

二、试题特点及教学建议

中考试题中的“事件的概率”，命题特点比较明晰，主要体现在题型多样，紧扣核心内容.比较历年的中考试卷，虽然在形式上推陈出新，但是在本质上基本稳定，都突出概率意义的理解和随机观念的培养，注重概率在解决实际问题中的作用.概率教学和考查的重点如图21所示.

2016—12—24

王华（1981—），男，中学一级教师，主要从事初中数学教学研究.