篱笆怎么围面积最大

祝立新

（浙江省江山市四都初级中学）

篱笆怎么围面积最大

祝立新

（浙江省江山市四都初级中学）

“综合与实践”是初中数学课程内容之一.选择、研制、开发并生成一个适合本地学生特点的恰当问题是实现“综合与实践”课程目标的载体.用篱笆围养鸡场是一个接近学生生活实际、易被学生操作理解，易于形成数学模型的综合性问题，对学生积累数学活动经验、培养学生应用意识和创新意识是有推动作用的.

综合与实践；数学模型；应用意识；创新意识

“综合与实践”是初中数学课程内容之一，是发展学生思维能力、培养应用意识和创新意识的重要抓手.一次研讨会上，笔者发现一个有关“综合与实践”方面的优秀题材.

题目有一堵长为12米的墙（图中阴影部分为墙），利用这堵墙和长为60米的篱笆围成一个矩形养鸡场，怎样围面积最大？最大面积为多少？

一、解决方案

这道题目看似简单，其实不然，整个问题解决过程要考虑多种情形，详解如下.

方案1：如图1，设平行于墙的篱笆长为x米，鸡场面积为y.

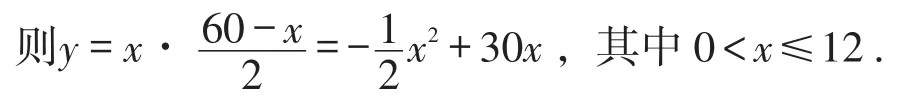
观察函数图象，当x=12时，可得鸡场面积最大为288米2.

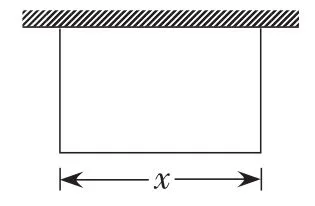
图1

图2

方案2：如图2，设墙左端篱笆长为x米，鸡场面积为y.

则y=（12+x）（24-x）=-x2+12x+288，其中0≤x＜24.

观察函数图象，当x=6时，可得鸡场面积最大为324米2.

方案3：如图3，只要把篱笆向左边平移成如图2所示即可.

图3

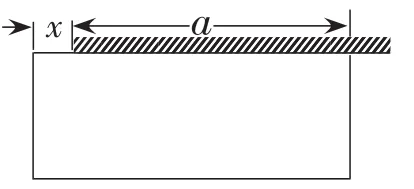
图4

方案4：如图4，考虑所用墙的长度，设所用墙的长度为a米，墙左端篱笆的长为x米，鸡场面积为y.

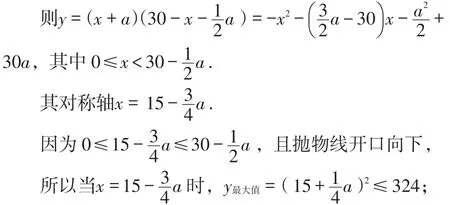
显然，当a=12时，鸡场面积的最大值为324米2.综合以上四种方案可知，当m=12米时，围成如图2所示的鸡场面积是最大的，最大面积为324米2.

二、反思引申

图5

图6

对于图1，只要墙足够长（不小于30米），那么当x=30时，鸡场面积的最大值为450米2.

三、拓展

篱笆怎么围所得矩形鸡场面积最大，这不仅与已知条件有关，还与篱笆的围法有关，不是一个单一结果，以下为笔者所做的系统归纳.

题目有一堵长为m的墙，利用这堵墙和长为60米的篱笆围成一个矩形养鸡场，怎样围使养鸡场面积最大？最大面积为多少？

四、试题撷英

例（2014年江苏·淮安卷）用长为32米的篱笆围一个矩形养鸡场，设围成的矩形一边长为x米，面积为y平方米．

（1）求y关于x的函数关系式；

（2）当x为何值时，围成的养鸡场面积为60平方米？

（3）能否围成面积为70平方米的养鸡场？如果能，求出其边长；如果不能，说明理由．

解析：第（1）小题根据矩形面积公式进行函数建模；第（2）（3）小题把y的值代入第（1）小题中的函数关系，求得相应的x值即可．

【点评】此题属于篱笆围法，是方案4中a＝0的情形，也可以根据拓展中的“当墙长m满足30＜m＜60时”的图4解答.

“综合与实践”课程内容是培养有实践能力、应用意识和创新意识人才的重要载体，所以开发适合于学生探究的“综合与实践”方面的课程内容具有重要意义.

［1］中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

［2］教育部基础教育课程教材专家工作委员会.《义务教育数学课程标准（2011年版）》解读［M］.北京：北京师范大学出版社，2012.

2016—11—08

祝立新（1970—），男，中学一级教师，主要从事初中数学教育和试题研究.