明道 优术 践行—关于在坐标系中求解三角形面积基本方法的探究
2017-03-28广东省东莞市寮步镇香市中学523400柯伟贤
广东省东莞市寮步镇香市中学(523400) 柯伟贤
明道 优术 践行—关于在坐标系中求解三角形面积基本方法的探究
广东省东莞市寮步镇香市中学(523400) 柯伟贤
在平面直角坐标系中求解三角形的面积是学习函数过程中常遇见的问题,也是历年中考常见的题型,这类问题的难度往往较大,学生常常因为没有掌握解决这类问题的基本方法,从而导致无法快速地解题或者直接无从下手.那么该如何有效地解决在函数问题中求解三角形的面积问题呢?本文就是针对这个问题对在坐标系中求解三角形面积进行了探究,给出了解决这一类问题的基本方法.
1 提炼解题题型,明思维之道
“明”即明白、懂得,“道”即规律、原则.“明道”即明白原则,掌握规律.“明道”要求教师要创设出“心愤口悱”的思维情景,让学生得到“举一反三”的解决问题的方法,因此问题题型的设计至关重要.
在问题解决的过程中,常常遇到一些对于解决问题有技术支撑的有效的基本思路,基本方法或基本结论,并且这些思路、方法、结论对这一类问题有帮助,则可以称之为“基本题型”,关于在坐标系中探究求解三角形面积的基本方法,这里选择了以下这四道题型.
例1.1 如图1,点A的坐标为(1,1),点B的坐标为(3,0)求S△OAB=?

例1.2 如图2,点A的坐标为(1,2),点B的坐标为(1,−1),点C的坐标为(0,1),求S△ABC=?
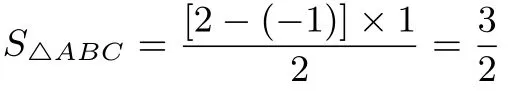
例1.3 如图3,点A的坐标为(2,1),点B的坐标为(−1,−2),线段AB交x轴,y轴于点D(1,0),C(0,−1),求S△OAB=?
分析:△OAB的三边都没有落在坐标轴上,也没有像例2一样有平行于坐标轴的边,那该怎么办呢?

图1
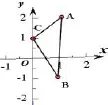
图2
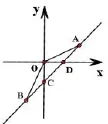
图3
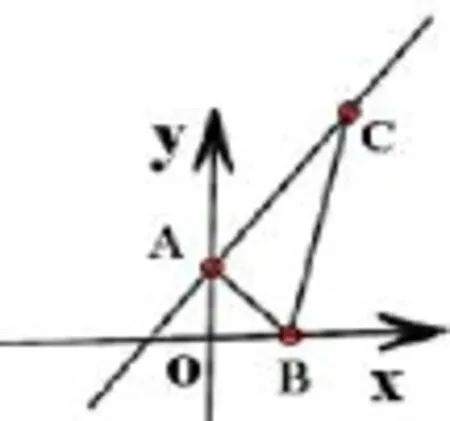
图4
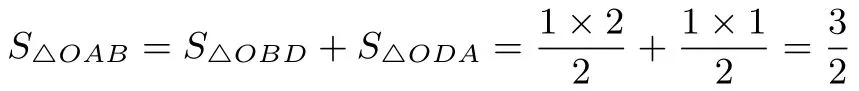
当然也可以选择顶点O过y轴把△OAB分成两个小三角形△OBC和△OAC,而这两个小三角形的公共边OC恰好落在x轴上,所以.
例1.4 如图4,直线y=x+1与x轴交于点A(0,1),点C(2,3)是直线y=x+1上的一个点,点B的坐标为(1,0),求S△ABC=?
分析:△ABC三边都没有落在坐标轴上,仿照例3选择合适的顶点把三角形进行分割,但是新的问题又来了,这个图不可以象例3那样可以通过x轴或者y轴把三角形分成两个小三角形,那又该怎么办呢?
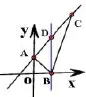
图5

这四道基本题型的设计由简单到复杂,包括了在坐标系中求解三角形面积的多种情况,学生可以由浅入深地进行学习,理解解决这一类问题的基本套路.让原本比较复杂的一类问题化归为同一种方法,从而使这一类问题变得有法可依.
2 形成解题技巧,优问题之术
“优术”即提升方法、技艺的水平,积累实用的策略,总结经验并从中发现规律.“优术”是“明道”后转化而来的具体操作方法,这需要归纳总结探究过程中的经验,优化解决问题的思路,形成解题技巧.
通过以上例题的学习,我们发现在坐标系中求解三角形面积的关键在于选择恰当的边作为三角形的底,因此可以得出在坐标系中求解三角形面积的基本方法是:当三角形有一边在落坐标轴上(或者有一边平行于坐标轴),则以这条边为底边,当三角形没有边落在坐标轴上(或者没有边平行坐标轴)时,则应该选择合适的顶点过坐标轴(或者是过顶点作平行坐标轴的直线)把三角形分割成两个有公共边的小三角形,利用两个小三角形的面积之和求解原三角形的面积.
优术,还在于教师要引领学生反思思维过程,优化解题方法.以上的四道基本题型中我们发现当三角形没有边落在坐标轴上(或者没有边平行坐标轴)时,当选择合适的顶点过坐标轴(或者是过顶点作平行于坐标轴的直线)把三角形分割成有公共边的两个小三角形,那么这个三角形的面积与这两个小三角形的公共边有什么关系呢?接下来进一步探讨以下这个基本图型.

图6

图7
如图6,△ABC没有边落在坐标轴上,选择过B点作平行于y轴的直线交AC于点D,直线BD把△ABC分成两个△ABD和△CBD,公共边BD,,由此得到
当然,如图7,我们也可以选择过C点作平行x轴的直线交AB于点E,由此得到
由此我们可以进一步优化在坐标系中求解三角形面积基本方法,如果三角形没有边落在坐标轴上(或者没有边平行于坐标轴)时,则应该选择合适的一顶点过坐标轴(或者是过顶点作平行于坐标轴的直线)把三角形分割成两个有公共边的小三角形,当直线在x轴上或平行于x轴,则三角形的面积=×公共边×另外两个点的垂直距离(即大纵坐标−小纵坐标).若这条直线在y轴上或平行于y轴,则三角形的面积=×公共边×另外两个点的水平距离(即大横坐标−小横坐标).
3 追求解题效率,践方法之行
“践行”就是积极实践各种理论和方法,学以致用.形成解题技巧后,就要在行动中考查方法的适用性和实用性,以提高解题的效率.经历以上的两个环节的学习,学生已经掌握了在函数中求解三角形面积的基本方法,接下来将精选历年的几道中考题,通过让践方法之行这个环节,学生学会知行合一,学以致用,提高解决这一类问题解题速度和解题质量.
例3.1(2013·浙江嘉兴)如图,一次函数y=kx+1(k0)与反比例函数的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
分析:(2)求△ABC的面积,观察发现△ABC的一边BC平行y轴,因此选择BC为底.
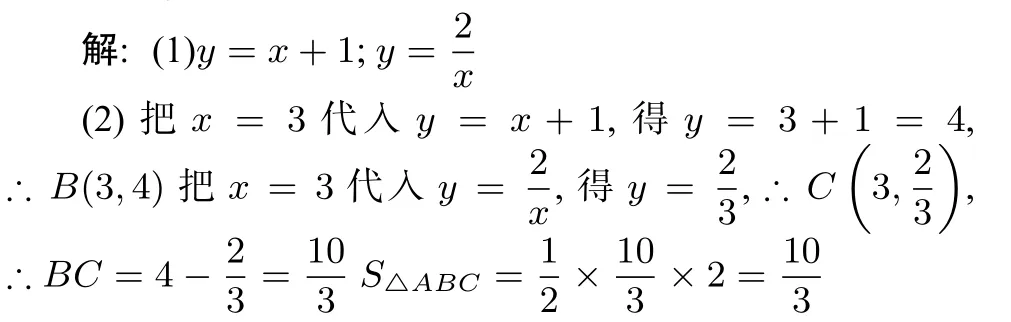
例3.2 (2015四川省巴中市)如图9,在平面直角坐标,一次函数y1=ax+b(a,b为常数,且a0)与反比例函数(m为常数,且m0)的图象交于点A(−2,1)、 B(1,n).
(1)求反比例函数和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
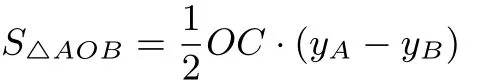

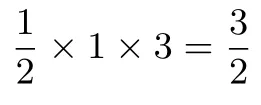

图8

图9
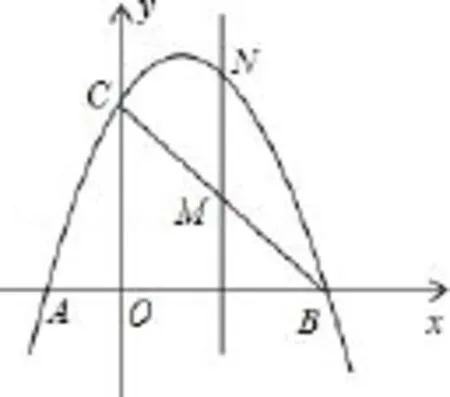
图10

图11
例3.4 (2012·黔东南州)如图10,已知抛物线经过点A(−1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN//y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.
分析:(3)如图11,求△BNC的面积,直线MN//y轴交BC于点M,把△BNC分成△CMN和△BMN,线段BC为公共边,所以S△BNC=S△MNC+S△MNB= MN·(xB−xC)
解:(1)抛物线的解析式y=−x2+2x+3
已知点M 的横坐标为m,则M(m,−m+3)、N(m,−m2+2m+3);故MN=−m2+2m+3−(−m+3)=−m2+3m(0<m<3)

(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
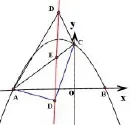
图13

“不愤不悱,不启不发”,通过以上“明道、优术、践行”这三个环节的学习,学生很好地掌握了在坐标系中求解三角形面积的基本方法,对这一类问题的解决获得了实践的经验,提高了解决这一类问题的速度,增强了学习数学的信心,而这一类问题的学习过程和方法对其他问题的学习也有很好地促进作用.
[1]章建跃.数学教学中的取势明道优术.中学数学(高中版)[J].2013(4):编后漫谈
[2]卜以楼.取势明道优术—初中函数图象的教学分析和思考.中学数学教学参考[J].2015(10):13-15
