例谈高中数学变式教学的策略与功能

广东广雅中学(510160) 赖淑明 吴新华

例谈高中数学变式教学的策略与功能

广东广雅中学(510160) 赖淑明 吴新华

1.提出问题和解决问题

数学变式就是从不同视角把握问题的本质,在变与不变中明辨问题的本质的一种解决问题的方式.数学是抽象而逻辑性较强的学科,变式能呈现数学的逻辑与思维,反映数学问题的本质,因而变式教学是数学教师在课堂上常用的教学形式之一.而合理的变式设置,会启发学生追根溯源,使学生的反思成为主动而迫切的行为,提高学生的思维品质.

椭圆的教学是圆锥曲线教学的难点,学生在椭圆的学习过程中普遍感觉知识点多而杂.此外,平面几何知识在思维突破上没有代数问题的客观具体,也没有立体几何的直观形象,学生难以捉摸和掌握.如果合理进行变式的设置,可以实现从直线与圆的问题的迁移到椭圆问题,深化对椭圆知识的理解.在合理的变式引导下,学生对椭圆的探索逐步升级,思考逐层深入,最终能够挖掘到问题的根源.

1.1概念引入的变式,反思概念的本质和拓展

问题1:请回忆高中课本中圆的定义.

一个动点到一个定点的距离为定值,这个定点的轨迹为圆.

思考:一个动点到两个定点的距离之比为定值(不等于1),这个动点的轨迹是什么?这是著名的阿波罗尼圆的定义.

变式1:一个动点到两个定点F1,F2的距离之和为定值,这个动点的轨迹是什么呢?这个动点的轨迹是椭圆.

由“一个动点到一个定点的距离”问题,到“一个动点到两个定点的距离”问题,通过变式,逐步探究,引出椭圆的定义.既有由已学的二次曲线定义进行承上启下,也有类比阿波罗尼圆的定义,加深对椭圆定义的认识.变式引入的过程,使椭圆的定义有了参照系:阿波罗尼圆,同时阿波罗尼圆的定义和椭圆定义的相似性,又会启发学生思考如下问题:

变式2:一个动点到两个定点F1,F2的距离之差为定值,这个动点的轨迹是什么呢?

当定值＜|F1F2|,动点的轨迹为双曲线的一支.

变式3:一个动点到两个定点F1,F2的距离之积为定值,这个动点的轨迹是什么呢?动点的轨迹为卡西尼卵形线.

1.2概念辨析的变式,反思概念的内涵和外延

问题2:设F1,F2为定点,|F1F2|=6,动点M满足|MF1|+|MF2|=10则动点M的轨迹是____

变式2:设F1(−3,0),F2(3,0),动点M满足|PF1|+|PF2|=6,则动点M的轨迹方程是___

反思1:“一个动点到两个定点的距离之和为定值”有几种表达方式?

尝试请学生列举自己知道的表达方式,通过反思引导学生把数学概念数学符号化.

反思2:椭圆定义的关键点是什么?

定值要大于两定点间的距离,即2a＞2c;若定值等于两定点间的距离,即2a=2c,则轨迹不是椭圆,而是一条线段.若定值小于两定点间的距离,即2a＜2c,则轨迹不存在.

1.3概念应用的变式,启发反思概念的等价性和转化

问题3:已知动圆P过定点A(−3,0),并且在圆F：(x−3)2+y2=64的内部与其相内切,试求动圆圆心P的轨迹方程.

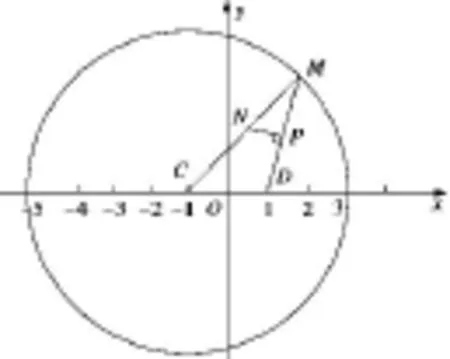
图1

变式1:已知M是以点C为圆心的圆(x+1)2+y2=8上的动点,定点D(1,0).线段DM的中垂线CM交于N,交DM于P,求动点N的轨迹方程.

变式2:设圆x2+y2+2x−15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.写出点E的轨迹方程.

变式3:已知圆C1：(x−4)2+y2=169,圆C2：(x+4)2+y2=9,动圆C与圆C1内切同时与圆C2外切,求动圆圆心的轨迹方程.

以上问题,借助变式,引导学生在各个不同的平面几何关系中,发现椭圆定义,加深对椭圆定义的理解.反思,动圆和定圆相切的问题,动圆中半径的中垂线问题等,都可以构造动点到两个定点的距离之和为定值.那么,除了以上的问题,我们还可如何构造椭圆的轨迹?引发学生对轨迹问题的等价转化的进一步思考.

1.4深化概念的变式,启发反思概念的多种结构和规律

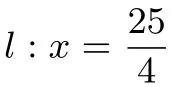
借助变式教学,拓展课本的例题,反思,把例题的结论一般化,归纳出椭圆的第二种定义:椭圆的第二种定义:一个动点M到一个定点的距离,与该点到一条定直线的距离的比为定值e,当0＜e＜1时,点M的轨迹为椭圆.

思考2:变式1的逆命题是否成立?

借助变式教学,进一步探索椭圆的第二定义的逆用,反思,获得椭圆第二定义的性质定理,如变式2和变式3的结论.

借助变式教学,拓展课本的例题,反思,把例题的结论一般化,归纳出椭圆的第三种定义:

思考2:变式1的逆命题是否成立?

思考3:变式2中两个定点A(−a,0),B(a,0)是否可以换成椭圆上的其它点?

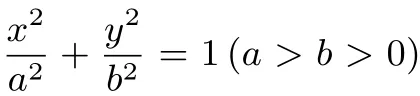
借助变式教学,进一步探索椭圆的第三定义的逆用,反思,获得椭圆第三定义的性质定理,即变式3的结论.

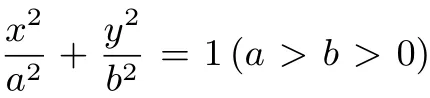
变式逐层递进,探索逐级上升,反思渐入佳境,对椭圆第三定义性质定理进行拓展,我们获得椭圆的中点弦定理,即变式4的结论.

通过概念变式的逐层深化,概念多种形式、多种命题的反复转换,启发学生反思概念的多种结构和规律,对概念有更综合和全面的理解.运用类比学习方式进一步激发学生在后续双曲线的学习中探索双曲线多维度的定义及性质.

2.深化问题和拓展问题

在多种椭圆问题解决中合理设置变式,进一步推动学生主动反思,形成能力.

2.1一个问题多种表征,反思问题的本源

例如:考查椭圆与以F1F2为直径的圆的位置关系的题型,很值得深入研究.

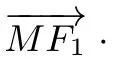
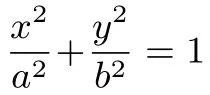
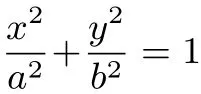
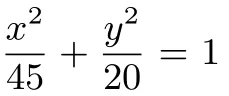
如果学生不能实现不同问题表征之间的相互转化,就不能达到解决一道题,理解一类题的目的.因此教师在教学过程中,借助变式呈现一类题的不同表征,有利于学生认识、辨别问题的异同,反思问题的本源,逐步提高数学理解能力,形成数学修养.

2.2一类问题多种载体,反思问题的迁移

唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题,就是将军饮马问题:诗中将军在观望烽火之后从山脚下的点A(1,1)出发,走到河边(河流所在位置x+2y+2=0)饮马后,再到点F(4,0)宿营,请问怎样走才能使总的路程最短?

问题7:已知点A(1,1)、F(4,0),P为直线l：x+2y+ 2=0上的动点,求|PA|+|PF|的最小值.

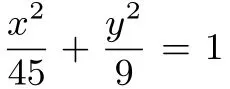
从问题的引入,到问题的变化,呈现了同类问题在不同载体中的变化,学生在问题生成的过程中,会不自觉地思考,在后续的学习中,河流是否也同样可以变成双曲线和抛物线呢?解决将军饮马问题的关键是:借助点关于直线对称转换研究的距离,再结合“三角形两边之和大于第三边,两边之差小于第三边”求得最值.而当河流改变为曲线之后,则借助曲线定义转换研究的距离,再结合“三角形两边之和大于第三边,两边之差小于第三边”求得最值.如果河流变为双曲线或抛物线时,是否可以同理推广?变式的过程实现问题的阶梯式上升,达到深化对问题求解过程的认识和反思.

2.3一种方法解决多种问题,反思问题的通法

点差法,是解决直线与椭圆问题的一个重要方法.从表面上看,点差法适用于解决与弦所在直线的斜率及弦的中点相关的问题.但,亦有很多看似不是中点弦问题,实质上可以转化为中点弦的问题.如椭圆上是否存在两点关于直线对称的问题,又如椭圆内接等腰三角形问题等.

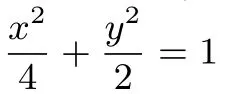
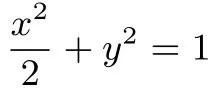
不同问题,本质一致.借助变式教学,让学生体会点差法在看似不同的问题中的应用,培养学生用联系的眼光研究问题,反思如何关联问题的各个条件,实现条件的准确转化,达到对解题方法由点到面的发散,形成学生自身认知系统对基础知识和典型方法的网络框架.

3.基本结论

变式教学是动态变化的教学过程,有效、准确、生动的变式能激发学生学习的热情,体验数学学习,反思数学方法及原理,探索数学问题的求解.变式教学贯穿始终的椭圆教学,反思成为教学课堂上的常态,这对促进学生研究椭圆的本质,构建圆锥曲线良好的认知结构,驾驭解析几何问题有着重要意义,也为后续其它曲线的学习打下良好的基础.

变式教学思维过程,检查得失,加深对数学原理、解法的认识,联系以往知识中有共同本质的东西,概括出带有普遍性的规律,从而培养学生思维的灵活性,提高学生的思维品质,努力培养学生创新意识和创造能力,全面提升学生数学素养.这是我们教学的不懈追求.

[1]刘雪颖.椭圆的变式教学研究[D].湖北:华中师范大学,2015.5

[2]李锦旭王.树运.从两道高考试题的背景说起[J].数学教学研究,2012(8)

[3]普通高中课程标准试验教科书数学[M].人民教育出版社2005